Chuyên đề công suất, hệ số công suất điện xoay chiều của mạch RLC, vật lí lớp 12
Câu 1.
Với \[\varphi \] là độ lệch pha của u và i trong mạch điện xoay chiều. Đại lượng nào sau đây được gọi là hệ số công suất của mạch điện xoay chiều?
[A]. \[sin\varphi . \]
[B]. \[cos\varphi . \]
[C]. tanφ.
[D]. cotφ.
Hệ số công suất của mạch điện xoay chiều là: $\cos \varphi $.
Câu 2.
Công suất của một đoạn mạch xoay chiều được tính bằng công thức nào dưới đây ?
[A]. P = U. I
[B]. \[P=Z. {{I}^{2}}\]
[C]. \[P=Z. {{I}^{2}}. cos\varphi \]
[D]. \[P=R. I. cos\varphi . \]
Công suất của một đoạn mạch xoay chiều được tính bằng công thức: $P=UI\cos \varphi =I. Z. I. \cos \varphi =Z. {{I}^{2}}. \cos \varphi $.
Câu 3.
Đặt điện áp \[u={{U}_{0}}cos(\omega t+\varphi )\] vào hai đầu đoạn mạch gồm điện trở thuận R và cuộn cảm thuần có độ tự cảm L mắc nối tiếp. Hệ số công suất của đoạn mạch là
[A]. $\dfrac{\omega L}{R}$.
[B]. $\dfrac{R}{\sqrt{{{R}^{2}}+{{(\omega L)}^{2}}}}$.
[C]. $\dfrac{R}{\omega L}$.
[D]. $\dfrac{\omega L}{\sqrt{{{R}^{2}}+{{(\omega L)}^{2}}}}$
Hệ số công suất của đoạn mạch là: \[\cos \varphi =\dfrac{R}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{(\omega L)}^{2}}}}\] .
Câu 4.
Trong đoạn mạch điện không phân nhánh gồm điện trở thuần R và tụ điện C, mắc vào điện áp xoay chiều\[u={{U}_{o}}cos(\omega t)V\]. Hệ số công suất của đoạn mạch là
[A]. $\dfrac{R}{R+\omega C}. $
[B]. $\dfrac{R}{R+\dfrac{1}{\omega C}}. $
[C]. $\dfrac{R}{\omega C}. $
[D]. $\dfrac{R}{\sqrt{{{R}^{2}}+\dfrac{1}{{{\omega }^{2}}{{C}^{2}}}}}. $
Hệ số công suất của đoạn mạch là: \[\cos \varphi =\dfrac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( \dfrac{1}{\omega C} \right)}^{2}}}}\].
Câu 5.
Trong đoạn mạch điện xoay chiều không phân nhánh RLC, đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \[u={{U}_{o}}cos(\omega t)V\]. Hệ số công suất của mạch là
[A]. $\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{\omega }^{2}}{{L}^{2}}-\dfrac{1}{{{\omega }^{2}}{{C}^{2}}} \right)}^{2}}}}. $
[B]. $\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( \omega L-\dfrac{1}{\omega C} \right)}^{2}}}}. $
[C]. $\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( \omega C-\dfrac{1}{\omega L} \right)}^{2}}}}. $
[D]. $\dfrac{\omega L-\omega C}{R}. $
Hệ số công suất của đoạn mạch là: \[\cos \varphi =\dfrac{R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( \omega L-\dfrac{1}{\omega C} \right)}^{2}}}}\].
Câu 6. ĐH2013
Đặt điện áp \[u={{U}_{0}}c\text{os}\left( 100\pi t-\dfrac{\pi }{12} \right)V\]vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở cuộn cảm và tụ điện thì cường độ dòng điện qua mạch là \[i={{I}_{0}}c\text{os}\left( 100\pi t+\dfrac{\pi }{12} \right)A\]. Hệ số công suất của đoạn mạch bằng:
[A]. 0,50
[B]. 0,87
[C]. 1,00
[D]. 0,71
\[cos\varphi =cos\left( {{\varphi }_{u}}{{\varphi }_{i}} \right)=\] $\dfrac{\sqrt{3}}{2}$.
Câu 7.
Đoạn mạch nối tiếp gồm cuộn cảm thuần và điện trở. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \[u={{U}_{0}}\cos \left( \omega t-\dfrac{\pi }{6} \right)\ (V)\] thì điện áp hai đầu cuộn cảm là \[{{u}_{L}}={{U}_{0L}}\cos \left( \omega t+\dfrac{\pi }{6} \right)\ (V). \] Hệ số công suất của mạch bằng
[A]. \[\dfrac{\sqrt{3}}{2}\]
[B]. \[0,5. \]
[C]. \[0,25. \]
[D]. $\dfrac{\sqrt{2}}{2}$
${{\varphi }_{i}}={{\varphi }_{{{u}_{L}}}}-\dfrac{\pi }{2}=-\dfrac{\pi }{3}$ \[\to cos\varphi =cos\left( {{\varphi }_{u}}{{\varphi }_{i}} \right)=\] $\dfrac{\sqrt{3}}{2}$.
Câu 8.
Đặt điện áp \[u={{U}_{0}}cos(100\pi t-\dfrac{\pi }{6})\left( V \right)\] vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì cường độ dòng điện qua mạch là \[i={{I}_{0}}cos(100\pi t+\dfrac{\pi }{6})\left( A \right). \] Hệ số công suất của đoạn mạch bằng
[A]. 0,50.
[B]. 0,86.
[C]. 1,00.
[D]. 0,71.
Hệ số công suất của đoạn mạch bằng: $\cos ({{\varphi }_{u}}-{{\varphi }_{i}})=\cos \left( -\dfrac{\pi }{3} \right)=\dfrac{1}{2}$ .
Câu 9. ĐH2015
Đặt điện áp xoay chiều có giá trị hiệu dụng 200 V vào đoạn mạch gồm cuộn cảm thuần mắc nối tiếp với điện trở thuần. Biết điện áp hiệu dụng ở hai đầu điện trở là 100 V. Hệ số công suất của đoạn mạch bằng
[A]. 0,8.
[B]. 0,7.
[C]. 1.
[D]. 0,5.
\[cos\varphi =\dfrac{{{U}_{R}}}{U}=0,5\].
Câu 10. CĐ2013
Khi có một dòng điện xoay chiều chạy qua cuộn dây có điện trở thuần 50 Ω thì hệ số công suất của cuộn dây bằng 0,8. Cảm kháng của cuộn dây đó bằng
[A]. 45,5 Ω.
[B]. 91,0 Ω.
[C]. 37,5 Ω.
[D]. 75,0 Ω.
\[cos\varphi =\] $\dfrac{r}{\sqrt{{{r}^{2}}+Z_{L}^{2}}}=0,8$ \[\to {{Z}_{L}}=37,5\Omega . \]
Câu 11. CĐ2011
Đặt điện áp $u=150\sqrt{2}\cos 100\pi t$(V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp thì điện áp hiệu dụng giữa hai đầu điện trở thuần là 150 V. Hệ số công suất của đoạn mạch là
[A]. $\dfrac{\sqrt{3}}{2}$.
[B]. 1.
[C]. $\dfrac{\sqrt{2}}{2}$.
[D]. $\dfrac{\sqrt{3}}{3}$.
Hệ số công suất của đoạn mạch là : \[cos\varphi =\dfrac{{{U}_{R}}}{U}=\dfrac{150}{150}=1\].
Câu 12.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R mắc nối tiếp với tụ điện có điện dung C. Biết điện áp hiệu dụng giữa hai đầu điện trở và giữa hai đầu tụ điện lần lượt là $100\sqrt{3}$ V và 100 V. Hệ số công suất của đoạn mạch là
[A]. $\dfrac{\sqrt{3}}{3}$ .
[B]. $\dfrac{\sqrt{2}}{2}$ .
[C]. $\dfrac{\sqrt{2}}{3}$.
[D]. $\dfrac{\sqrt{3}}{2}$ .
$U=\sqrt{U_{R}^{2}+U_{C}^{2}}=200$V \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{\sqrt{3}}{2}$.
Câu 13. CĐ2013
Một đoạn mạch điện xoay chiều gồm điện trở thuần mắc nối tiếp với tụ điện. Biết điện áp hiệu dụng giữa hai đầu tụ điện bằng một nửa điện áp hiệu dụng ở hai đầu đoạn mạch. Hệ số công suất của đoạn mạch bằng
[A]. 0,87.
[B]. 0,92.
[C]. 0,50.
[D]. 0,71.
Ta có $U=\sqrt{U_{R}^{2}+U_{C}^{2}}=\sqrt{U_{R}^{2}+{{\left( \dfrac{U}{2} \right)}^{2}}}\to {{U}_{R}}=\dfrac{\sqrt{3}}{2}U$
Câu 14.
Một đoạn mạch gồm một điện trở thuần mắc nối tiếp với một tụ điện. Biết hệ số công suất của đoạn mạch là 0,5. Tỉ số giữa dung kháng và điện trở R là
[A]. $\sqrt{2}. $
[B]. $\sqrt{3}. $
[C]. $\dfrac{1}{\sqrt{2}}. $
[D]. $\dfrac{1}{\sqrt{3}}. $
$\cos \varphi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=0,5\to {{Z}_{C}}=R\sqrt{3}$.
Câu 15.
Đặt điện áp xoay chiều vào đoạn mạch gồm RLC mắc nối tiếp (cuộn cảm thuần) thì điện áp hiệu dụng trên R, L và C lần lượt là \[{{U}_{R}}=120V;{{U}_{L}}=50Vv\grave{a}{{U}_{C}}=100V\] thì hệ số công suất của mạch là
[A]. \[\dfrac{\sqrt{2}}{2}\]
[B]. 0,85
[C]. \[\dfrac{\sqrt{3}}{2}\]
[D]. 0,92
$U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=130$V \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{12}{13}$.
Câu 16.
Đặt vào hai đầu đoạn mạch RLC không phân nhánh một điện áp xoay chiều\[u={{U}_{0}}cos(\omega t)V\] . Kí hiệu \[{{U}_{R}},{{U}_{L}},{{U}_{C}}\] tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần R, cuộn dây thuần cảm (cảm thuần) L và tụ điện C. Nếu \[{{U}_{R}}=0,5{{U}_{L}}={{U}_{C}}\] thì hệ số công suất của mạch là
[A]. \[\dfrac{1}{\sqrt{3}}. \]
[B]. \[\dfrac{\sqrt{3}}{2}. \]
[C]. \[\dfrac{1}{\sqrt{2}}. \]
[D]. \[\dfrac{1}{2}. \]
+ Đặt \[{{U}_{R}}=0,5{{U}_{L}}={{U}_{C}}=1\to {{U}_{L}}=2\]
+ $U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=\sqrt{2}$ \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{\sqrt{2}}{2}$.
Câu 17.
Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch RLC mắc nối tiếp (cuộn cảm thuần) thì điện áp hiệu dụng có mối liên hệ \[U={{U}_{C}}=2{{U}_{L}}\] . Hệ số công suất mạch điện là
[A]. $\dfrac{\sqrt{2}}{2}. $
[B]. 1.
[C]. $\dfrac{\sqrt{3}}{2}. $
[D]. 0,5.
+ Đặt \[U={{U}_{C}}=2{{U}_{L}}=2\to {{U}_{L}}=1\]
+ $U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=2$ \[\to {{U}_{R}}=\] $\sqrt{3}$ \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{\sqrt{3}}{2}$.
Câu 18.
Đặt một điện áp $u=U\sqrt{2}\cos \omega t$(V) vào hai đầu đoạn mạch RCL theo thứ tự mắc nối tiếp (cuộn cảm thuần) thì thấy điện áp hiệu dụng $U={{U}_{L}}=\dfrac{{{U}_{RC}}}{\sqrt{3}}$. Hệ số công suất của mạch điện là
[A]. 0,5.
[B]. $\dfrac{\sqrt{3}}{2}$.
[C]. $\dfrac{\sqrt{2}}{2}$.
[D]. $\dfrac{1}{3}$.
+ Đặt $U={{U}_{L}}=\dfrac{{{U}_{RC}}}{\sqrt{3}}=1$→ ${{U}_{RC}}=\sqrt{U_{R}^{2}+U_{C}^{2}}=\sqrt{3}\to U_{R}^{2}+U_{C}^{2}=3$ (*)
+ $U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=1\to U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}=1$ (**) Trừ từng vế (*) – (**)→ $U_{C}^{2}-{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}=2\Leftrightarrow U_{C}^{2}-{{\left( 1-{{U}_{C}} \right)}^{2}}=2\Leftrightarrow 2{{U}_{C}}-1=2\Leftrightarrow {{U}_{C}}=1,5\to {{U}_{R}}=\dfrac{\sqrt{3}}{2}$ \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{\sqrt{3}}{2}$.
Câu 19.
Đặt vào hai đầu đoạn mạch RLC không phân nhánh một điện áp xoay chiều \[u={{U}_{o}}cos(\omega t)V\]. Kí hiệu \[{{U}_{R}},{{U}_{L}},{{U}_{C}}\] tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần R, cuộn dây thuần cảm (cảm thuần) L và tụ điện C. Khi $\dfrac{2\sqrt{3}}{3}{{U}_{R}}=2{{U}_{L}}={{U}_{C}}$thì hệ số công suất của mạch là
[A]. \[\dfrac{1}{\sqrt{3}}. \]
[B]. \[\dfrac{\sqrt{3}}{2}. \]
[C]. \[\dfrac{1}{\sqrt{2}}. \]
[D]. \[\dfrac{1}{2}. \]
+ Đặt $\dfrac{2\sqrt{3}}{3}{{U}_{R}}=2{{U}_{L}}={{U}_{C}}=1$ \[\to {{U}_{L}}=0,5;\] ${{U}_{R}}=\dfrac{\sqrt{3}}{2}$
+ $U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=1$ \[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=\dfrac{\sqrt{3}}{2}$.
Câu 20.
Điện áp đặt vào hai đầu đoạn mạch LRC nối tiếp mắc theo thứ tự thì điện áp hiệu dụng ${{U}_{RL}}=\dfrac{1}{2}{{U}_{RC}}. $ Biết ${{\text{R}}^{2}}=\dfrac{L}{C}$. Hệ số công suất của đoạn mạch có giá trị là
[A]. $\dfrac{\sqrt{13}}{4}. $
[B]. $\dfrac{2}{\sqrt{13}}. $
[C]. $\sqrt{\dfrac{3}{13}}. $
[D]. \[\dfrac{3}{\sqrt{13}}. \]
+ ${{\text{R}}^{2}}=\dfrac{L}{C}={{Z}_{L}}{{Z}_{C}}$; Đặt R = 1 → \[{{\text{Z}}_{L}}=\dfrac{1}{{{Z}_{C}}}\]
+ ${{U}_{RL}}=\dfrac{1}{2}{{U}_{RC}}\Leftrightarrow {{Z}_{RL}}=\dfrac{1}{2}{{Z}_{RC}}\Leftrightarrow \sqrt{{{R}^{2}}+Z_{L}^{2}}=\dfrac{1}{2}\sqrt{{{R}^{2}}+Z_{C}^{2}}\Leftrightarrow 2\sqrt{1+Z_{L}^{2}}=\sqrt{1+\dfrac{1}{Z_{L}^{2}}}\Leftrightarrow 4\text{Z}_{L}^{4}+3Z_{L}^{2}-1=0$ → ${{Z}_{L}}=\dfrac{1}{2}$→ \[{{Z}_{C}}=2\] → \[\text{Z}=\dfrac{\sqrt{13}}{2}\] \[\to cos\varphi =\] $\dfrac{R}{Z}=\dfrac{2}{\sqrt{13}}$.
Câu 21.
Điện áp đặt vào hai đầu đoạn mạch LRC nối tiếp mắc theo thứ tự thì điện áp hiệu dụng ${{U}_{RL}}=\sqrt{3}{{U}_{RC}}. $ Biết ${{\text{R}}^{2}}=\dfrac{L}{C}$. Hệ số công suất của đoạn mạch có giá trị là
[A]. $\dfrac{\sqrt{2}}{7}. $
[B]. $\dfrac{\sqrt{3}}{5}. $
[C]. $\sqrt{\dfrac{3}{7}}. $
[D]. $\dfrac{\sqrt{2}}{5}. $
+ ${{\text{R}}^{2}}=\dfrac{L}{C}={{Z}_{L}}{{Z}_{C}}$; Đặt R = 1 → \[{{\text{Z}}_{L}}=\dfrac{1}{{{Z}_{C}}}\]
+ ${{U}_{RL}}=\sqrt{3}{{U}_{RC}}\Leftrightarrow {{Z}_{RL}}=\sqrt{3}{{Z}_{RC}}\Leftrightarrow \sqrt{{{R}^{2}}+Z_{L}^{2}}=\sqrt{3{{R}^{2}}+3Z_{C}^{2}}\Leftrightarrow \sqrt{1+Z_{L}^{2}}=\sqrt{3+\dfrac{3}{Z_{L}^{2}}}\Leftrightarrow \text{Z}_{L}^{4}-2Z_{L}^{2}-3=0$ → ${{Z}_{L}}=\sqrt{3}$→${{Z}_{C}}=\dfrac{1}{\sqrt{3}}$ → \[\text{Z}=\sqrt{\dfrac{7}{3}}\] \[\to cos\varphi =\] $\dfrac{R}{Z}=\sqrt{\dfrac{3}{7}}$.
Câu 22.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R, cuộn dây thuần cảm L và tụ điện C mắc nối tiếp. Biết điện áp hiệu dụng giữa hai đầu các phần tử theo thứ tự trên lần lượt là 40 V, 80 V, 50 V. Hệ số công suất của đoạn mạch
[A]. 0,8.
[B]. 0,6.
[C]. 0,25.
[D]. 0,71.
$U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=50$V\[\to cos\varphi =\] $\dfrac{{{U}_{R}}}{U}=0,8$.
Câu 23.
Đặt điện áp \[u=200\cos 100\pi t\ (V)\] vào hai đầu một đoạn mạch gồm điện trở thuần R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Dòng điện trong mạch có cường độ là \[i=4\cos \left( 100\pi t-\dfrac{\pi }{3} \right)\ (A). \] Giá trị của R bằng
[A]. \[50\sqrt{2\ }\Omega . \]
[B]. \[50\ \Omega . \]
[C]. \[25\sqrt{2\ }\Omega . \].
[D]. \[25\ \Omega . \]
\[\text{Z}=\dfrac{{{U}_{0}}}{{{I}_{0}}}=50\]Ω → $\cos \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=0,5=\dfrac{R}{Z}\to R=25\Omega $.
Câu 24. ĐH2015
Câu 24(ĐH-2015): Đặt điện áp $u=200\sqrt{2}\cos 100\pi t$(V) vào hai đầu một điện trở thuần 100 Ω. Công suất tiêu thụ của điện trở bằng
[A]. 800 W.
[B]. 200 W.
[C]. 300 W.
[D]. 400 W.
w\[\text{P}=\dfrac{U_{R}^{2}}{R}=400\]W.
Câu 25.
Đặt vào hai đầu đoạn mạch xoay chiều RLC nối tiếp điện áp xoay chiều \[u=120\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{6} \right)(V)\] thì cường độ dòng điện trong mạch \[i=3\sqrt{2}\cos \left( 100\pi t+\dfrac{\pi }{6} \right)(A). \] Điện trở R của mạch bằng
[A]. $20\sqrt{3}$Ω.
[B]. $20\sqrt{2}$Ω.
[C]. 40 Ω.
[D]. 20 Ω.
\[\text{Z}=\dfrac{{{U}_{0}}}{{{I}_{0}}}=40\]Ω → $\cos \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=0,5=\dfrac{R}{Z}\to R=20$Ω.
Câu 26. CĐ2008
Dòng điện có dạng i = sin100πt (A) chạy qua cuộn dây có điện trở thuần 10 Ω và hệ số tự cảm L. Công suất tiêu thụ trên cuộn dây là
[A]. 10 W.
[B]. 9 W.
[C]. 7 W.
[D]. 5 W.
\[\text{P}={{I}^{2}}r=5\]W.
Câu 27. ĐH2014
Dòng điện có cường độ $i=2\sqrt{2}\cos 100\pi t$(A) chạy qua điện trở thuần 100 Ω. Trong 30 giây, nhiệt lượng tỏa ra trên điện trở là
[A]. 8485 J.
[B]. 4243 J.
[C]. 12 kJ.
[D]. 24 kJ.
\[\text{P}={{I}^{2}}R=400\]W \[\to Q=P. \Delta t=12kJ. \]
Câu 28.
Đặt vào hai đầu một đoạn mạch điện xoay chiều một điện áp u= 100cos100πt (V) thì cường độ dòng điện qua đoạn mạch là $i=2\cos \left( 100\pi t+\dfrac{\pi }{3} \right)$ A. Công suất tiêu thụ trong đoạn mạch này là
[A]. $100\sqrt{3}$W.
[B]. 50 W.
[C]. $50\sqrt{3}$W.
[D]. 100 W.
\[\text{P}=UI\cos \varphi =50\]W.
Câu 29. ĐH2009
Đặt vào hai đầu đoạn mạch điện RLC không phân nhánh một điện áp $u=220\sqrt{2}\cos \left( \omega t-\dfrac{\pi }{2} \right)$(V) thì cường độ dòng điện qua đoạn mạch có biểu thức là $i=2\sqrt{2}\cos \left( \omega t-\dfrac{\pi }{4} \right)$(A). Công suất tiêu thụ của đoạn mạch là
[A]. 440 W.
[B]. $220\sqrt{2}$W.
[C]. $440\sqrt{2}$W.
[D]. 220 W.
\[\text{P}=UI\cos \varphi =220\sqrt{2}\]W.
Câu 30. CĐ2009
Đặt điện áp $u=100\cos \left( \omega t+\dfrac{\pi }{6} \right)$(V) vào hai đầu đoạn mạch có điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp thì dòng điện qua mạch là $i=2\cos \left( \omega t+\dfrac{\pi }{3} \right)$ (A). Công suất tiêu thụ của đoạn mạch là
[A]. $100\sqrt{3}$W.
[B]. 50 W.
[C]. $50\sqrt{3}$ W.
[D]. 100 W.
\[\text{P}=UI\cos \varphi =50\sqrt{3}\]W.
Câu 31.
Đặt điện áp $u=120\sin \left( 100\pi t+\dfrac{\pi }{3} \right)$ (V) vào hai đầu một đoạn mạch thì dòng điện trong mạch có biểu thức $i=4\cos \left( 100\pi t+\dfrac{\pi }{6} \right)$(A). Công suất tiêu thụ của đoạn mạch là
[A]. $240\sqrt{3}$W.
[B]. 120 W.
[C]. 240 W.
[D]. $120\sqrt{3}$W.
$u=120\sin \left( 100\pi t+\dfrac{\pi }{3} \right)$V = $120\cos \left( 100\pi t-\dfrac{\pi }{6} \right)$V → \[\text{P}=UI\cos \varphi =120\]W.
Câu 32.
Đặt vào hai đầu đoạn mạch xoay chiều điện áp $u=180\cos \left( 100\pi t-\dfrac{\pi }{6} \right)\left( V \right)$ thì cường độ dòng điện qua mạch $i=2\sin \left( 100\pi t+\dfrac{\pi }{6} \right)\left( A \right)$. Công suất tiêu thụ trên đoạn mạch bằng
[A]. $90\sqrt{3}$W.
[B]. 90 W.
[C]. 360 W.
[D]. 180 W.
$i=2\sin \left( 100\pi t+\dfrac{\pi }{6} \right)A=2\cos \left( 100\pi t-\dfrac{\pi }{3} \right)A$ → \[\text{P}=UI\cos \varphi =90\sqrt{3}\]W.
Câu 33.
Mạch điện xoay chiều gồm điện trở R = 100 Ω, cuộn dây thuần cảm có cảm kháng bằng 100 W, tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{\pi }F$ mắc nối tiếp. Đặt vào hai đầu mạch điên một điện áp xoay chiều u = 200cos(100πt) V. Công suất tiêu thụ bởi đoạn mạch này có giá trị
[A]. 200 W.
[B]. 400 W.
[C]. 100 W.
[D]. 50 W.
\[\text{Z}=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\] 100 Ω → $I=\dfrac{U}{Z}=\sqrt{2}$A → \[\text{P}={{I}^{2}}R=200\]W.
Câu 34.
Đặt điện áp xoay chiều có giá trị hiệu dụng 50 V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 10 Ω và cuộn cảm thuần. Biết điện áp hiệu dụng ở hai đầu cuộn cảm thuần là 30 V. Công suất tiêu thụ trong đoạn mạch bằng
[A]. 120 W.
[B]. 320 W.
[C]. 240 W.
[D]. 160 W.
\[{{\text{U}}_{R}}=\sqrt{{{U}^{2}}-U_{L}^{2}}=\] 40 V → \[\text{P}=\dfrac{U_{R}^{2}}{R}=160\]W.
Câu 35.
Đoạn mạch AB gồm điện trở R = 80 Ω, tụ điện$C=\dfrac{{{2. 10}^{-4}}}{\pi }\,F$và cuộn dây thuần cảm có độ tự cảm $L=\dfrac{1,1}{\pi }\,H$ mắc nối tiếp. Đặt vào hai đầu đoạn mạch AB điện áp xoay chiều $u=200\cos \left( 100\pi t+\dfrac{\pi }{3} \right)\,V. $ Công suất tiêu thụ trên đoạn mạch AB là
[A]. 200 W.
[B]. 120 W.
[C]. 100 W.
[D]. 160 W.
\[\text{Z}=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\] 100 Ω → $I=\dfrac{U}{Z}=\sqrt{2}$A → \[\text{P}={{I}^{2}}R=160\]W.
Câu 36.
Đặt điện áp x$u=220\sqrt{2}\cos 100\pi t$(V) vào hai đầu một điện trở thuần thì công suất điện tiêu thụ của điện trở là 1100 W. Biểu thức cường độ dòng điện chạy qua điện trở là
[A]. i =10cos100πt (A).
[B]. i = 5cos100πt (A).
[C]. $i=5\sqrt{2}\cos 100\pi t$(A).
[D]. $i=10\sqrt{2}\cos 100\pi t$ (A).
Mạch chỉ có R nên: \[\text{P}=UI\to I=5\text{A}\]\[\to {{I}_{0}}=\] \[5\sqrt{2}\]A →$i=5\sqrt{2}\cos 100\pi t$A.
Câu 37.
Đoạn mạch AB gồm điện trở R = 100 Ω, tụ điện $C=\dfrac{{{10}^{-4}}}{\pi \sqrt{3}}\,F$ và cuộn dây thuần cảm có độ tự cảm $L=\dfrac{2\sqrt{3}}{\pi }\,H$ mắc nối tiếp. Đặt vào hai đầu đoạn mạch AB điện áp xoay chiều $u=220\sqrt{2}\cos \left( 100\pi t \right)\,V. $Điện năng mà đoạn mạch tiêu thụ trong một giờ là
[A]. 360 kWh.
[B]. 0,121 kWh.
[C]. 6 kWh.
[D]. 360 kWh.
\[\text{Z}=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\] 200 Ω → $I=\dfrac{U}{Z}=1,1$A → \[\text{P}={{I}^{2}}R=121\]W \[\to Q=P. \Delta t=0,121kWh\] (0,121 “số điện”)
Câu 38. CĐ2009
Đặt điện áp $u=100\sqrt{2}\cos \omega t$ (V), có $\omega $ thay đổi được vào hai đầu đoạn mạch gồm điện trở thuần 200 $\Omega $ , cuộn cảm thuần có độ tự cảm $\dfrac{25}{36\pi }$H và tụ điện có điện dung $\dfrac{{{10}^{-4}}}{\pi }$F mắc nối tiếp. Công suất tiêu thụ của đoạn mạch là 50 W. Giá trị của $\omega $ là
[A]. 150 p rad/s.
[B]. 50p rad/s.
[C]. 100p rad/s.
[D]. 120p rad/s.
$P=\dfrac{{{\left( U\cos \varphi \right)}^{2}}}{R}$ \[\to cos\varphi =1\to \] Cộng hưởng: $\omega =\dfrac{1}{\sqrt{LC}}$ \[=120\pi \left( rad/s \right). \] Cách khác: $P=\dfrac{{{U}^{2}}R}{{{R}^{2}}+{{\left( \omega L-\dfrac{1}{\omega C} \right)}^{2}}}\to \omega =120\pi $rad/s
Câu 39.
Đặt điện áp $u=100\sqrt{2}\cos 100\pi t$(V) vào hai đầu đoạn mạch gồm điện trở thuần 50 $\Omega $ , cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung $\dfrac{{{10}^{-3}}}{2\pi }$F mắc nối tiếp. Công suất tiêu thụ trên mạch là 200 W. Giá trị của L là
[A]. $\dfrac{1}{\pi }$ H.
[B]. $\dfrac{1}{2\pi }$ H.
[C]. $\dfrac{1}{5\pi }$ H.
[D]. $\dfrac{1}{3\pi }$ H.
$P=\dfrac{{{\left( U\cos \varphi \right)}^{2}}}{R}$ \[\to cos\varphi =1\to \] Cộng hưởng: $L=\dfrac{1}{{{\omega }^{2}}C}=\dfrac{1}{5\pi }$H.
Câu 40.
Đặt điện áp có tần số f vào hai đầu đoạn mạch gồm điện trở thuần 50 $\Omega $ , cuộn cảm thuần có độ tự cảm $\dfrac{5}{3\pi }$H và tụ điện có điện dung $\dfrac{{{10}^{-4}}}{3\pi }$F mắc nối tiếp. Hệ số công suất của mạch là $\cos \varphi =0,707$. Giá trị của f là
[A]. 90 Hz.
[B]. 60 Hz.
[C]. 45 Hz.
[D]. 120 Hz.
$\cos \varphi =\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( \omega L-\dfrac{1}{\omega C} \right)}^{2}}}}=0,707$ \[\to \omega =120\pi \to f=60Hz. \]
Câu 41. CĐ2012
Đặt điện áp $u={{U}_{o}}c\text{os}\left( \omega t+\dfrac{\pi }{3} \right)$(V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức $i=\sqrt{6}\cos \left( \omega t+\dfrac{\pi }{6} \right)$(A) và công suất tiêu thụ của đoạn mạch bằng 150 W. Giá trị \[{{U}_{0}}\] bằng
[A]. 100 V.
[B]. $100\sqrt{3}$V.
[C]. 120 V.
[D]. $100\sqrt{2}$V.
$P=UI\cos \varphi \to U=100$V \[\to {{U}_{0}}=\] $100\sqrt{2}$.
Câu 42.
Cho đoạn mạch RC nối tiếp có R = 15 $\Omega $ . Khi cho dòng điện xoay chiều \[i={{I}_{0}}cos\left( 100\pi t \right)\left( A \right)\] qua mạch thì điện áp hiệu dụng hai đầu mạch AB là ${{U}_{AB}}=50\,V,\ {{U}_{C}}=\dfrac{4}{3}{{U}_{R}}$. Công suất của mạch điện là
[A]. 60 W.
[B]. 80 W.
[C]. 100 W.
[D]. 120 W.
$U=\sqrt{U_{R}^{2}+U_{C}^{2}}\to {{U}_{R}}=$ 30 V → $P=\dfrac{U_{R}^{2}}{R}=60$W.
Câu 43.
Một đoạn mạch điện gồm một điện trở thuần mắc nối tiếp với một tụ điện. Điện áp xoay chiều đặt vào hai đầu đoạn mạch có giá trị hiệu dụng 150 V, tần số 100 Hz. Dòng điện chạy trong mạch có giá trị hiệu dụng 1 A. Công suất tiêu thụ trong đoạn mạch là 120 W. Điện dung của tụ điện là
[A]. 17,68 μF.
[B]. 37,35 μF.
[C]. 74,60 μF.
[D]. 32,57 μF.
$P={{I}^{2}}R$→ \[R=120\Omega \to {{U}_{R}}=120V\to {{U}_{C}}=90V\to {{Z}_{C}}=90\Omega \to C=17,68\mu F. \]
Câu 44.
Đặt điện áp xoay chiều $u=120\sqrt{2}c\text{os}\left( 100\pi t+\dfrac{\pi }{3} \right)V$vào hai đầu đoạn mạch gồm cuộn dây thuần cảm L, một điện trở R và một tụ điện có $C=\dfrac{{{10}^{3}}}{2\pi }\mu F$ mắc nối tiếp. Biết điện áp hiệu dụng trên cuộn dây L và trên tụ điện C bằng nhau và bằng một nửa trên R. Công suất tiêu thụ trên đoạn mạch bằng
[A]. 720 W
[B]. 360 W
[C]. 240 W
[D]. 360 W
Tính \[{{Z}_{C}}=20\Omega !\] Mà \[{{U}_{L}}={{U}_{C}}=0,5{{U}_{R}}\to {{Z}_{L}}={{Z}_{C}}=0,5R\] \[\to R=40\Omega \] và mạch có \[{{Z}_{L}}={{Z}_{C}}\] nên đang cộng hưởng điện → $P=\dfrac{{{U}^{2}}}{R}=360$W .
Câu 45.
Đặt điện áp xoay chiều $u=200\sqrt{2}\cos 100\pi t$(V) vào hai đầu một đoạn mạch AB gồm điện trở thuần 100 Ω, cuộn cảm thuần và tụ điện mắc nối tiếp. Khi đó, điện áp hai đầu tụ điện là ${{u}_{c}}=100\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)$ (V). Công suất tiêu thụ của đoạn mạch AB bằng
[A]. 200 W.
[B]. 400 W.
[C]. 300 W.
[D]. 100 W.
${{\varphi }_{i}}={{\varphi }_{{{u}_{C}}}}+\dfrac{\pi }{2}=0={{\varphi }_{u}}$ → cộng hưởng điện → $P=\dfrac{{{U}^{2}}}{R}=400$W(\[{{U}_{0C}}=\] $100\sqrt{2}$V bài cho ko cần dùng).
Câu 46.
Đặt điện áp xoay chiều có giá trị hiệu dụng 80 V và tần số 50 Hz vào hai đầu đoạn mạch RLC mắc nối tiếp. Biết: $L=\dfrac{0,6}{\pi }H$;$C=\dfrac{{{10}^{-4}}}{\pi }F$. Công suất tiêu thụ của mạch là 80 W. Giá trị điện trở R là
[A]. 40 W.
[B]. 80 W.
[C]. 20 W.
[D]. 30 W.
$P=\dfrac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\to R=$40 Ω.
Câu 47. ĐH2007
Đặt điện áp $u=100\sqrt{2}\sin 100\pi t$(V) vào hai đầu đoạn mạch RLC không phân nhánh, cuộn cảm thuần có độ tự cảm là $\dfrac{1}{\pi }$H. Khi đó điện áp hiệu dụng ở hai đầu mỗi phần tử R, L và C có độ lớn như nhau. Công suất tiêu thụ của đoạn mạch là
[A]. 100 W.
[B]. 200 W.
[C]. 250 W.
[D]. 350 W.
Tính \[{{Z}_{L}}=100\Omega !\] Mà \[{{U}_{L}}={{U}_{C}}={{U}_{R}}\to {{Z}_{L}}={{Z}_{C}}=R=100\Omega \] Mạch có \[{{Z}_{L}}={{Z}_{C}}\] nên đang cộng hưởng điện → $P=\dfrac{{{U}^{2}}}{R}=100$W .
Câu 48.
Đặt điện áp $u=120\sqrt{2}\cos 100\pi t$ (V) vào hai đầu đoạn mạch RLC không phân nhánh, R = 50 Ω. Độ lệch pha giữa dòng điện và điện áp u là $\dfrac{\pi }{3}$. Công suất tiêu thụ của đoạn mạch là
[A]. 72 W.
[B]. 288 W.
[C]. 48 W.
[D]. 144 W.
$P=\dfrac{{{\left( U\cos \varphi \right)}^{2}}}{R}=72$W .
Câu 49.
Đặt điện áp \[u=100\sqrt{2}\cos 100\pi t\] (V) vào hai đầu đoạn mạch AB gồm điện trở thuần 50 \[\Omega \], cuộn cảm thuần và tụ điện mắc nối tiếp. Khi đó, điện áp giữa hai đầu cuộn cảm thuần có biểu thức \[{{u}_{L}}=200\cos \left( 100\pi t+\dfrac{\pi }{2} \right)\](V). Công suất tiêu thụ của đoạn mạch AB bằng
[A]. 300 W.
[B]. 400 W.
[C]. 200 W.
[D]. 100 W.
${{\varphi }_{i}}={{\varphi }_{{{u}_{L}}}}-\dfrac{\pi }{2}=0={{\varphi }_{u}}$ → cộng hưởng điện → $P=\dfrac{{{U}^{2}}}{R}=200$W.
Câu 50.
Cho mạch điện xoay RLC có R thay đổi được. Cuộn dây thuần cảm có \[L=\dfrac{1}{\pi }H,\ C=\dfrac{{{10}^{-3}}}{4\pi }F\], điện áp hiệu dụng hai đầu mạch là \[u=75\sqrt{2}c\text{os}\left( 100\pi t \right)V. \]Công suất tiêu thụ trong mạch P = 45 W. Điện trở R có thể có những giá trị nào sau:
[A]. R = 45 Ω hoặc R = 60 Ω.
[B]. R = 80 Ω hoặc R = 160 Ω.
[C]. R = 45 Ω hoặc R = 80 Ω.
[D]. R = 60 Ω hoặc R = 160 Ω.
$P=\dfrac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\to R=$40 Ω hoặc 80 Ω.
Câu 51.
Cuộn dây có độ tự cảm $L=\dfrac{2}{15\pi }H$ và điện trở r = 12 Ω mắc nối tiếp được đặt vào một điện áp xoay chiều có điện áp hiệu dụng 100 V và tần số 60 Hz. Nhiệt lượng toả ra trên cuộn dây trong một phút là
[A]. 15 kJ.
[B]. 12 kJ.
[C]. 18 kJ.
[D]. 24 kJ.
\[\text{Z}=\sqrt{{{r}^{2}}+Z_{L}^{2}}=\] 20 Ω \[\to I=5A\to 300W\to Q=P. \Delta t=300. 60=18kJ. \]
Câu 52.
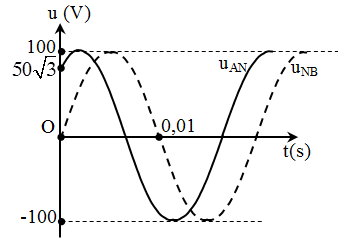
Cho đoạn mạch xoay chiều AB gồm đoạn mạch AN nối tiếp với đoạn mạch NB. Cho dòng điện có cường độ $i=2\sqrt{2}\cos \left( \omega t-\dfrac{\pi }{6} \right)$A chạy qua mạch, thì điện áp trên AM và MB có đồ thị được mô tả trên hình vẽ bên (\[{{u}_{AN}}\] được biểu diễn đường nét đứt, \[{{u}_{NB}}\] được biểu diễn đường nét liền). Xác định công suất tiêu thụ của mạch AB gần giá trị nào nhất:
[A]. 200 W
[B]. 150 W
[C]. 250 W
[D]. 350 W
Đọc đồ thị: ${{u}_{AN}}=100\cos \left( 100\pi t-\dfrac{\pi }{6} \right)$V và${{u}_{NB}}=100\cos \left( 100\pi t-\dfrac{\pi }{2} \right)$V \[\to {{u}_{AB}}={{u}_{AN}}+{{u}_{NB}}=\] $100\sqrt{3}\cos \left( 100\pi t-\dfrac{\pi }{3} \right)$→ \[P=UIcos\varphi =212,13W. \]
Câu 53.
Một mạch điện xoay chiều gồm điện trở thuần R = 40 $\Omega $ , một cuộn dây thuần cảm có độ tự cảm \[\dfrac{0,6}{\pi }\]H và tụ điện C mắc nối tiếp. Đặt vào hai đầu đoạn mạch đó một điện áp xoay chiều \[u=80\sqrt{2}\cos \left( 100\pi t+\dfrac{\pi }{6} \right)V\]thì công suất tiêu thụ trên đoạn mạch đó bằng 160 W. Biểu thức điện áp trên tụ điện là
[A]. \[{{u}_{C}}=240\cos \left( 100\pi t-\dfrac{\pi }{3} \right)V\]
[B]. \[{{u}_{C}}=80\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)V\]
[C]. \[{{u}_{C}}=240\cos \left( 100\pi t-\dfrac{\pi }{6} \right)V\]
[D]. \[{{u}_{C}}=120\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{3} \right)V\]
$P=\dfrac{{{\left( U\cos \varphi \right)}^{2}}}{R}\to \cos \varphi =1$ : Mạch có cộng hưởng điện \[\to {{Z}_{L}}={{Z}_{C}}=60\Omega \] và \[{{\varphi }_{u}}={{\varphi }_{i}}=\] $\dfrac{\pi }{6}$ → ${{\varphi }_{{{u}_{C}}}}={{\varphi }_{i}}-\dfrac{\pi }{2}=-\dfrac{\pi }{3}$; $\dfrac{{{U}_{0C}}}{{{U}_{0}}}=\dfrac{{{Z}_{C}}}{Z}\to {{U}_{0C}}=120\sqrt{2}$V. Vậy: \[{{u}_{C}}=120\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{3} \right)V\].
Câu 54.
Đặt điện áp xoay chiều $u=200\cos \left( 100\pi t+\dfrac{\pi }{3} \right)$(V) vào đoạn mạch gồm điện trở thuần R = 40 Ω, một cuộn dây thuần cảm và tụ điện có điện dung \[C=\dfrac{{{2. 10}^{-4}}}{\pi }F\] mắc nối tiếp thì công suất tiêu thụ của đoạn mạch bằng 500 W. Biểu thức điện áp giữa hai đầu cuộn cảm thuần là
[A]. ${{u}_{L}}=250\cos \left( 100\pi t+\dfrac{2\pi }{3} \right)$(V).
[B]. ${{u}_{L}}=125\sqrt{2}\cos \left( 100\pi t+\dfrac{5\pi }{6} \right)$(V).
[C]. ${{u}_{L}}=125\sqrt{2}\cos \left( 100\pi t+\dfrac{2\pi }{3} \right)$(V).
[D]. ${{u}_{L}}=250\cos \left( 100\pi t+\dfrac{5\pi }{6} \right)$(V).
$P=\dfrac{{{\left( U\cos \varphi \right)}^{2}}}{R}\to \cos \varphi =1$ : Mạch có cộng hưởng điện \[\to {{Z}_{L}}={{Z}_{C}}=50\Omega \] và \[{{\varphi }_{u}}={{\varphi }_{i}}=\] $\dfrac{\pi }{3}$ → ${{\varphi }_{{{u}_{L}}}}={{\varphi }_{i}}+\dfrac{\pi }{2}=\dfrac{5\pi }{6}$; $\dfrac{{{U}_{0C}}}{{{U}_{0}}}=\dfrac{{{Z}_{C}}}{Z}\to {{U}_{0C}}=250$V. Vậy: ${{u}_{L}}=250\cos \left( 100\pi t+\dfrac{5\pi }{6} \right)$.
Câu 55. CĐ2011
Đặt điện áp $u=220\sqrt{2}\cos 100\pi t$(V) vào đoạn mạch gồm một bóng đèn dây tóc loại 110V – 50W mắc nối tiếp với một tụ điện có điện dung C thay đổi được. Điều chỉnh C để đèn sáng bình thường. Độ lệch pha giữa cường độ dòng điện và điện áp ở hai đầu đoạn mạch lúc này là
[A]. $\dfrac{\pi }{3}$
[B]. $\dfrac{\pi }{4}$.
[C]. $\dfrac{\pi }{6}$.
[D]. $\dfrac{\pi }{2}$
Đèn dây tóc 110V – 55W (\[{{U}_{M}}{{P}_{M}}\] ) ta coi như điện trở có R = $\dfrac{U_{ĐM}^{2}}{{{P}_{ĐM}}}=220$Ω và \[{{I}_{M}}=\] $\dfrac{{{P}_{ĐM}}}{{{U}_{ĐM}}}=0,5\text{A}$ → Đèn sáng bình thường khi dòng điện hiệu dụng trong mạch là \[I={{I}_{M}}=0,5A\to Z=440\Omega \] \[\to cos\varphi =\] $\dfrac{R}{Z}=\dfrac{1}{2}$ \[\to \varphi =\] $\dfrac{\pi }{3}$..
Câu 56.
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Điện áp hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Hệ số công suất cosφ của mạch là
[A]. 0,5.
[B]. $\dfrac{\sqrt{3}}{2}. $
[C]. $\dfrac{\sqrt{2}}{2}. $
[D]. $\dfrac{1}{4}. $
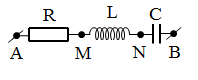
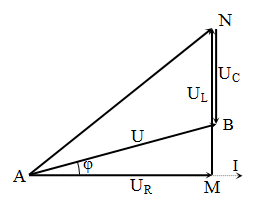
→ Dễ thấy $\varphi =\dfrac{\pi }{6}$ → $\cos \varphi =\dfrac{\sqrt{3}}{2}$.
Câu 57.
Đặt điện áp xoay chiều $u=100\sqrt{2}c\text{os}\left( 100\pi t \right)V$vào hai đầu đoạn mạch nối tiếp gồm cuộn dây không thuần cảm có \[r=50\Omega \], L=\[\dfrac{0,4}{\pi }\] (H); tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{\pi }F$ và điện trở thuần R = 30 Ω. Công suất tiêu thụ trên đoạn mạch và trên điện trở R lần lượt là:
[A]. P = 28,8 W; \[{{P}_{R}}=10,8W\]
[B]. P = 80 W; \[{{P}_{R}}=30W\]
[C]. P = 160 W; \[{{P}_{R}}=30W\]
[D]. P = 57,6 W; \[{{P}_{R}}=31,6W\]
Công suất toàn mạch: $P={{I}^{2}}\left( R+r \right)=\dfrac{{{U}^{2}}\left( R+r \right)}{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=80$W; Công suất trên R: $P={{I}^{2}}R=\dfrac{{{U}^{2}}R}{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=30$W.
Câu 58.
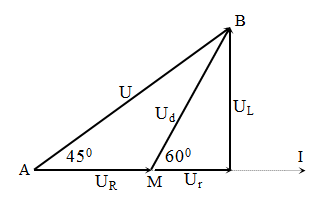
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện được đặt vào điện áp xoay chiều có giá trị hiệu dụng U thì điện áp hiệu dụng giữa hai đầu cuộn dây là $\dfrac{4U}{3}$ và điện áp hiệu dụng giữa hai đầu tụ điện là $\dfrac{7U}{15}$. Hệ số công suất của cuộn dây là
[A]. 0,48.
[B]. 0,64.
[C]. 0,56.
[D]. 0,6.
Hệ số công suất cuộn dây là: $\cos {{\varphi }_{d}}=\dfrac{r}{{{Z}_{d}}}=\dfrac{{{U}_{r}}}{{{U}_{d}}}$ Đặt \[U=1\to {{U}_{d}}=\] $\dfrac{4}{3}$ và \[{{U}_{C}}=\] $\dfrac{7}{15}$. Ta có: ${{U}_{d}}=\sqrt{U_{r}^{2}+U_{L}^{2}}=\dfrac{4}{3}\to U_{r}^{2}+U_{L}^{2}=\dfrac{16}{9}$(*) ; $U=\sqrt{U_{r}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}$ = 1 → $U_{r}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}=1$(**) Trừ từng vế (*) – (**), ta có: $U_{L}^{2}-{{\left( {{U}_{L}}-\dfrac{7}{15} \right)}^{2}}=\dfrac{7}{9}\Leftrightarrow \dfrac{14{{U}_{L}}}{15}-\dfrac{49}{225}=\dfrac{7}{9}\Rightarrow {{U}_{L}}=\dfrac{16}{15}\Rightarrow {{U}_{r}}=\dfrac{4}{5}$ → $\cos {{\varphi }_{d}}=\dfrac{{{U}_{r}}}{{{U}_{d}}}=0,6$.
Câu 59.

Đặt điện áp xoay chiều $u=U\sqrt{2}\cos \omega t$ (V) vào hai đầu đoạn mạch RLC mắc nối tiếp (cuộn dây thuần cảm) thấy i chậm pha hơn u, \[{{U}_{RL}}=\] $\sqrt{3}$U và \[{{u}_{RL}}\] sớm pha hơn u là $\dfrac{\pi }{6}$. Hệ số công suất của đoạn mạch bằng
[A]. $\dfrac{\sqrt{2}}{2}$.
[B]. $\dfrac{1}{\sqrt{5}}$.
[C]. $\dfrac{\sqrt{3}}{2}$.
[D]. $\dfrac{1}{\sqrt{3}}$.

Đặt AB = 1 → AN = $\sqrt{3}$ mà $\widehat{NAB}=\dfrac{\pi }{6}$ → NB = 1 \[\to \Delta ANB\] cân tại B → $\varphi =\dfrac{\pi }{6}$ → $\cos \varphi =\dfrac{\sqrt{3}}{2}$.
Câu 60.
Đoạn mạch điện gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha giữa điện áp giữa hai đầu cuộn dây, \[{{U}_{d}}\] và dòng điện là$\dfrac{\pi }{3}$. Gọi điện áp giữa hai đầu tụ điện là \[{{U}_{C}}\], ta có ${{U}_{C}}=\sqrt{3}{{U}_{d}}$. Hệ số công suất của mạch điện là
[A]. $\dfrac{\sqrt{2}}{2}. $
[B]. 0,5.
[C]. $\dfrac{\sqrt{3}}{2}. $
[D]. $\dfrac{1}{4}. $
Đặt \[{{U}_{R}}=1\to \] $\tan \left( {{\varphi }_{{{u}_{d}}}}-{{\varphi }_{i}} \right)=\dfrac{{{U}_{L}}}{{{U}_{R}}}=\sqrt{3}\to {{U}_{L}}=\sqrt{3}$ \[\to {{U}_{d}}=\] $\sqrt{U_{r}^{2}+U_{L}^{2}}$ = 2 \[\to {{U}_{C}}=\] $2\sqrt{3}$ → U = 2. → \[\cos {{\varphi }_{d}}=\dfrac{{{U}_{R}}}{U}=0,5\].
Câu 61.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm một cuộn dây mắc nối tiếp với một tụ điện. Điện áp hiệu dụng giữa hai đầu cuộn dây có giá trị bằng điện áp hiệu dụng giữa hai bản tụ điện. Dòng điện tức thời trong đoạn mạch chậm pha $\dfrac{\pi }{4}$ so với điện áp tức thời giữa hai đầu cuộn dây. Hệ số công suất của đoạn mạch là
[A]. 0,707.
[B]. 0,866.
[C]. 0,924.
[D]. 0,999.
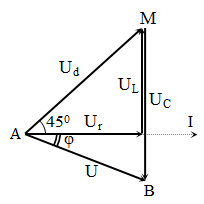
Bài cho \[{{U}_{d}}={{U}_{C}}\to \varphi =22,{{5}^{0}}\] →$\cos \varphi \approx 0,924$ . .
Câu 62.
Đặt điện áp xoay chiều có giá trị hiệu dụng 120 V vào hai đầu một đoạn mạch gồm cuộn dây không thuần cảm và tụ điện có điện dung C mắc nối tiếp. Hệ số công suất của đoạn mạch là 0,8. Hệ số công suất của cuộn dây là 0,6. Điện áp hiệu dụng hai đầu cuộn dây bằng
[A]. 80 V
[B]. 160 V
[C]. 60 V
[D]. 240 V
\[cos\varphi =0,8=\] $\dfrac{{{U}_{r}}}{U}\to {{U}_{r}}=96$V. Lại có: \[cos{{\varphi }_{d}}=0,6=\] $\dfrac{{{U}_{r}}}{{{U}_{d}}}\to {{U}_{d}}=160$V.
Câu 63.
Cho đoạn mạch nối tiếp theo thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn dây có độ tự cảm L, điện trở r. Biết $L=C{{R}^{2}}=C{{r}^{2}}$ Đặt vào đoạn mạch điện áp xoay chiều $u=U\sqrt{2}c\text{os}\omega t\text{ }\left( V \right)$ thì điện áp hiệu dụng của đoạn mạch RC gấp $\sqrt{3}$ lần điện áp hiệu dụng hai đầu cuộn dây. Hệ số công suất của đoạn mạch là
[A]. 0,866.
[B]. 0,657.
[C]. 0,785.
[D]. 0,5.
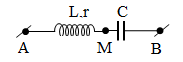

+ $L=C{{\text{R}}^{2}}=C{{\text{r}}^{2}}\to {{R}^{2}}={{r}^{2}}={{Z}_{L}}{{Z}_{C}}\to \dfrac{r}{{{Z}_{L}}}=\dfrac{{{Z}_{C}}}{R}$ Hay $\dfrac{MK}{KB}=\dfrac{ME}{A\text{E}}$ \[\to \Delta AEM\tilde{\ }\Delta BKM\to \] \[\widehat{\text{A}M\text{E}}=\widehat{BMK}\] \[\to \Delta AMB\] vuông tại M → $\tan \widehat{BAM}=\dfrac{MB}{AM}=\dfrac{1}{\sqrt{3}}\to \widehat{BAM}={{30}^{0}}$
+ R = r → AE = EP → N là trung điểm AB → MN = AN = NB →$\widehat{AME}={{30}^{0}}\to \widehat{EAM}={{60}^{0}}\to \widehat{IAB}={{30}^{0}}$\[\to cos\varphi \approx 0,866\]
Câu 64.
Đặt điện áp xoay chiều $u=U\sqrt{2}\cos \omega t$ (V) vào hai đầu đoạn mạch AB. Cuộn cảm có điện trở r = R. Điện áp hiệu dụng trên AB và NB bằng nhau. Hệ số công suất của cuộn dây là \[cos{{\varphi }_{d}}=0,6\] . Hệ số công suất của cả đoạn mạch là
[A]. 0,923.
[B]. 0,683.
[C]. 0,752.
[D]. 0,854.
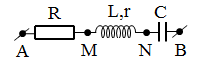
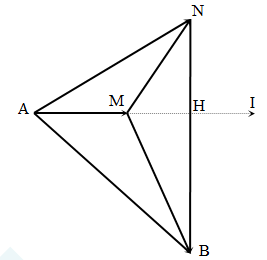
+ Bài cho: AB = NB, $\cos {{\varphi }_{d}}=\dfrac{MH}{MN}=0,6$→ $\dfrac{NH}{MN}=0,8$(*) Đặt MH = 1 → AH = 2 và MN = $\dfrac{5}{3}$, do đó (*) → NH = $\dfrac{4}{3}$ → \[\widehat{\text{A}NH}\approx 56,{{31}^{0}}\] và \[\widehat{NAH}\approx 33,{{69}^{0}}\]
+ \[\Delta ANB\] cân tại B → $\varphi =\widehat{IAB}=22,62$ → $\cos \varphi \approx 0,923$.
Câu 65.
Đặt điện áp $u=70\sqrt{2}\cos \left( 100\pi t \right)V$vào hai đầu đoạn mạch gồm một cuộn dây có điện trở r = 5 Ω và độ tự cảm $L=\dfrac{0,35}{\pi }(H)$ mắc nối tiếp với điện trở thuần R = 30 Ω. Công suất tiêu thụ của đoạn mạch là
[A]. $35\sqrt{2}\,\text{W}. $
[B]. 70 W.
[C]. 35 W.
[D]. $30\sqrt{2}\,\text{W}. $
Công suất tỏa ra trên đoạn mạch: $P={{I}^{2}}\left( R+r \right)=\dfrac{{{U}^{2}}\left( R+r \right)}{{{\left( R+r \right)}^{2}}+Z_{L}^{2}}=70$W.
Câu 66.
Đoạn mạch xoay chiều gồm điện trở \[{{R}_{0}}\] mắc nối tiếp với một hộp kín X. Khi đặt vào hai đầu mạch một điện áp xoay chiều có giá trị hiệu dung U thì điện áp hiệu dụng hai đầu \[{{R}_{0}}\] và hộp X lần lượt là 0,8U và 0,5U. Hệ số công suất của mạch chính bằng
[A]. 0,87.
[B]. 0,67.
[C]. 0,50.
[D]. 0,71.
Không mất tính tổng quát, giả sử đoạn mạch X có tính cảm kháng. $\cos \varphi =\dfrac{{{U}^{2}}+U_{R0}^{2}-U_{X}^{2}}{2U. {{U}_{R0}}}=0,86875$.
Câu 67.
Một mạch điện xoay chiều gồm một cuộn dây được mắc nối tiếp với một điện trở R = 100 Ω. Điện áp hiệu dụng hai đầu mạch $U=50\sqrt{3}$V, hai đầu cuộn dây \[{{U}_{d}}=50V\] , hai đầu điện trở \[{{U}_{R}}=50V\] . Công suất tiêu thụ điện của mạch bằng
[A]. 50 W.
[B]. 12,5 W.
[C]. 25 W.
[D]. 37,5 W.
+ $I=\dfrac{{{U}_{R}}}{R}=$ 0,5A.
+ $U=\sqrt{{{\left( {{U}_{R}}+{{U}_{r}} \right)}^{2}}+U_{L}^{2}}=50\sqrt{3}$V → ${{\left( {{U}_{R}}+{{U}_{r}} \right)}^{2}}+U_{L}^{2}=7500$; ${{U}_{d}}=\sqrt{U_{r}^{2}+U_{L}^{2}}=50V\to U_{r}^{2}+U_{L}^{2}=2500$ →\[{{\left( 50+{{U}_{r}} \right)}^{2}}-U_{r}^{2}=5000\to {{U}_{r}}=25V\]→$r=\dfrac{{{U}_{r}}}{I}=50$ Ω. → $P={{I}^{2}}\left( R+r \right)=37,5$W
Câu 68.
Mạch điện xoay chiều gồm điện trở thuần R = 20 Ω mắc nối tiếp với cuộn dây. Đặt vào hai đầu mạch một điện áp xoay chiều có điện áp hiệu dụng U và tần số f. Điện áp hiệu dụng ở hai đầu cuộn dây là\[{{U}_{d}}=90V\] . Dòng điện trong mạch lệch pha $\dfrac{\pi }{6}$ so với điện áp hai đầu đoạn mạch và lệch pha $\dfrac{\pi }{3}$ so với điện áp hai đầu cuộn dây Công suất tiêu thụ điện của đoạn mạch bằng
[A]. 900 W.
[B]. 405 W.
[C]. 607,5 W.
[D]. 346,5 W.
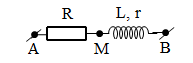
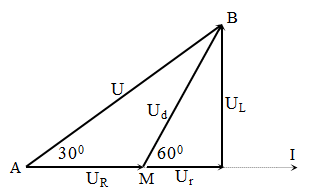
Dễ thấy \[\Delta AMB\] cân tại M với góc \[AMB={{120}^{0}}\] →$U=90\sqrt{3}\text{ }V$và \[{{U}_{R}}={{U}_{d}}=90V\to \] $I=\dfrac{{{U}_{R}}}{R}=4,5\text{ A}$ →$P=UI\cos \varphi $=607,5W.
Câu 69.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch AB nối tiếp. Đoạn mạch AN chứa cuộn dây thuần cảm L và điện trở R; đoạn mạch MB chứa R và C. Biết\[{{U}_{AN}}=100V\] , \[{{U}_{MB}}=75V\] , I =\[\sqrt{2}\]A và \[{{u}_{AN}}\] vuông pha với\[{{u}_{M}}_{B}\] Nội dung nào sau đây là sai ?
[A]. Công suất tiêu thụ của mạch là $30\sqrt{2}$W
[B]. Điện áp \[{{u}_{AB}}\] sớm pha hơn i
[C]. Giá trị của Z\[{{Z}_{L}}\] là $40\sqrt{2}$W
[D]. Công suất tiêu thụ của mạch là \[60\sqrt{2}\]W
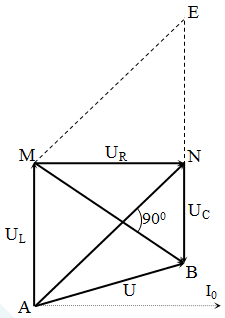
+ Bài cho \[{{u}_{AN}}\] vuông pha với \[{{u}_{MB}}!\]
+ Kẻ giản đồ vectơ: AN = $100\text{ }V$và MB = 75 V
+ Kẻ thêm đường thẳng qua M // AN cắt BN tại E. Dễ thấy: ME = AN = 100 V. Xét ∆MEB vuông tại M có MN là đường cao. →$\dfrac{1}{M{{N}^{2}}}=\dfrac{1}{M{{E}^{2}}}+\dfrac{1}{M{{B}^{2}}}\to {{U}_{\text{R}}}=MN=60\text{ V}$ → R = $30\sqrt{2}$ Ω → $P=\dfrac{U_{R}^{2}}{R}=60\sqrt{2}$W → (A sai!) ${{U}_{L}}=AM=\sqrt{A{{N}^{2}}-M{{N}^{2}}}=80\text{ V}$ \[\to {{Z}_{L}}=\] $40\sqrt{2}$Ω (C đúng!)
Câu 70.
Một cuộn dây không thuần cảm. Nếu mắc cuộn dây vào điện áp không đổi 20 V thì cường độ dòng điện qua cuộn dây là 3 A, còn nếu mắc vào điện áp xoay chiều 40 V – 50 Hz thì cường độ dòng điện hiệu dụng qua cuộn dây bằng 3,6 A. Hệ số công suất của cuộn dây là
[A]. 0,5.
[B]. 0,6.
[C]. 0,7.
[D]. 0,8.
+ Khi mắc nguồn một chiều: $r=\dfrac{{{U}_{DC}}}{{{I}_{DC}}}=\dfrac{20}{3}$Ω.
+ Khi mắc nguồn xoay chiều: ${{Z}_{d}}=\dfrac{U}{I}=\dfrac{100}{9}$Ω = $\sqrt{{{r}^{2}}+Z_{L}^{2}}$→ Hệ số công suất: $\cos {{\varphi }_{d}}=\dfrac{r}{{{Z}_{d}}}=0,6$.
Câu 71.
Mắc điện trở thuần vào nguồn điện không đổi U = 12 V thì cường độ dòng điện qua điện trở là 1,2 A. Nếu cho dòng điện xoay chiều chạy quay điện trở đó trong 30 phút thì nhiệt lượng tỏa ra là 900 kJ. Giá trị cực đại của dòng điện xoay chiều đó là?
[A]. 0,22 A.
[B]. 10 A.
[C]. 0,32 A.
[D]. 7,07 A.
+ Khi mắc nguồn một chiều: $R=\dfrac{{{U}_{DC}}}{{{I}_{DC}}}=10$Ω.
+ Khi mắc nguồn xoay chiều: \[Q=P. \Delta t\to P=500W={{I}^{2}}R\to I=5\sqrt{2}\to {{I}_{0}}=10A. \]
Câu 72.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R = 20 Ω mắc nối tiếp với cuộn dây. Điện áp hiệu dụng trên hai đầu cuộn dây là 90 V, dòng điện trong mạch lệch pha $\dfrac{\pi }{4}$so với điện áp hai đầu đoạn mạch và lệch pha $\dfrac{\pi }{3}$so với điện áp hai đầu cuộn dây. Công suất tiêu thụ của đoạn mạch là
[A]. 230 W.
[B]. 128,4 W.
[C]. 425 W.
[D]. 346,5 W.
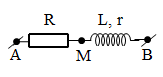
Dễ thấy \[\Delta AMB\] có góc \[AMB={{120}^{0}}\] , Theo định lý hàm sin → $U=45\sqrt{6}\text{ }V$và \[{{U}_{R}}=\]$-45+45\sqrt{3}$ (V) → $I=\dfrac{{{U}_{R}}}{R}=\dfrac{-9+9\sqrt{3}}{4}\text{ A}$ → $P=UI\cos \varphi $ = 128,4 W.
Câu 73.
Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R = 40 $\Omega $ mắc nối tiếp với cuộn cảm thuần có \[L=\dfrac{0,4}{\pi }H\], đoạn mạch MB là tụ điện có điện dung C. Đặt vào A, B điện áp xoay chiều \[{{u}_{AB}}=80\sqrt{5}\cos (100\pi t)\](V) thì điện áp hiệu dụng ở hai đầu đoạn mạch MB là \[120\sqrt{2}\]V. Công suất tiêu thụ trên AB là
[A]. 40W hoặc 160W.
[B]. 80W hoặc 320W.
[C]. 80W hoặc 160W.
[D]. 160W hoặc 320W.
$\dfrac{{{U}_{C}}}{U}=\dfrac{{{Z}_{C}}}{Z}\to $ \[\dfrac{3\sqrt{5}}{5}=\dfrac{{{Z}_{C}}}{\sqrt{{{40}^{2}}+{{\left( 40-{{Z}_{C}} \right)}^{2}}}}\to 4Z_{C}^{2}-720{{\text{Z}}_{C}}+28800=0\] \[\to {{Z}_{C}}=60\Omega \] hoặc \[120\Omega . \]
+ Nếu \[{{Z}_{C}}=60\Omega \to \] $I=\dfrac{{{U}_{C}}}{{{Z}_{C}}}=2\sqrt{2}$ A \[\to P={{I}^{2}}R=320W. \]
+ Nếu \[{{Z}_{C}}=120\Omega \to \] $I=\dfrac{{{U}_{C}}}{{{Z}_{C}}}=\sqrt{2}$ A \[\to P={{I}^{2}}R=80W. \] .
Câu 74. MH2017
Cho đoạn mạch gồm điện trở, cuộn dây và tụ điện mắc nối tiếp. Đặt điện áp$u=65\sqrt{2}\cos 100\pi t$(V) vào hai đầu đoạn mạch thì điện áp hiệu dụng ở hai đầu điện trở, hai đầu cuộn dây, hai đầu tụ điện lần lượt là 13 V, 13 V, 65 V. Hệ số công suất của đoạn mạch bằng
[A]. $\dfrac{1}{5}$.
[B]. $\dfrac{12}{13}$ .
[C]. $\dfrac{5}{13}$.
[D]. $\dfrac{4}{13}$.
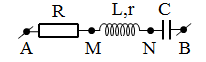
Bài cho: AM = MN = 13 V, AB = NB = 65 V. Đặt ME = x→$NE=\sqrt{{{13}^{2}}-{{x}^{2}}}$ Xét \[\Delta ABE: \] \[A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}}\Rightarrow {{65}^{2}}={{\left( 13+x \right)}^{2}}+{{\left( 65-\sqrt{{{13}^{2}}-{{x}^{2}}} \right)}^{2}}\] → x = 12 V → $\cos \varphi =\dfrac{AE}{AB}=\dfrac{12+13}{65}=\dfrac{5}{13}$.
Câu 75.
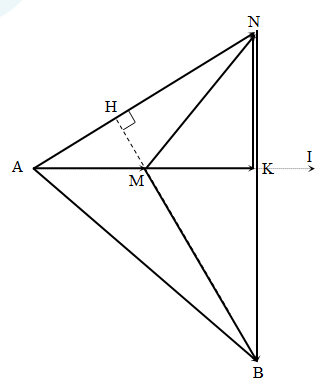
Đặt một điện áp \[{{u}_{AB}}={{U}_{0}}cos\omega t\left( V \right)\] vào 2 đầu đoạn mạch nối tiếp AB gồm điện trở R, cuộn dây có điện trở thuần r = R và một tụ điện C. Điểm M nằm giữa điện trở R và cuộn dây, điểm N nằm giữa cuộn dây với tụ điện C thì thấy 2 điện áp \[{{u}_{AN}},{{u}_{MB}}\] vuông pha nhau và có cùng giá trị hiệu dụng. Hệ số công suất của mạch điện là
[A]. 0,5.
[B]. $\dfrac{\sqrt{3}}{2}$.
[C]. $\dfrac{\sqrt{2}}{2}$.
[D]. $\dfrac{1}{3}$.
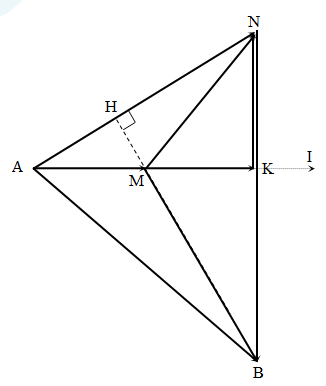
Ta có: \[\Delta AKN=\Delta BKM\left( g. c. g \right)\to \] MK = NK và BK = AK.
+ Do R = r → AM = MK → AK = 2NK → \[\text{A}N=\dfrac{AK\sqrt{5}}{2}\]
+ BK = AK→ \[\Delta ABK\] vuông cân tại K → \[\text{A}B=AK\sqrt{2}\to \cos \varphi =\dfrac{\sqrt{2}}{2}\].
Câu 76.
Cho đoạn mạch AB gồm hai đoạn mạch AM nối tiếp MB. Đoạn mạch AM gồm điện trở R nối tiếp với tụ điện có điện dung C, đoạn mạch MB có cuộn cảm có độ tự cảm L và điện trở r. Đặt vào AB một điện áp xoay chiều $u=U\sqrt{2}\cos \left( \omega t \right)V. $ Biết $R=r=\sqrt{\dfrac{L}{C}};\ {{U}_{AM}}=2{{U}_{MB}}. $ Hệ số công suất của đoạn mạch có giá trị là
[A]. $\dfrac{\sqrt{3}}{2}. $
[B]. $\dfrac{\sqrt{2}}{2}. $
[C]. $\dfrac{3}{5}. $
[D]. $\dfrac{4}{5}. $
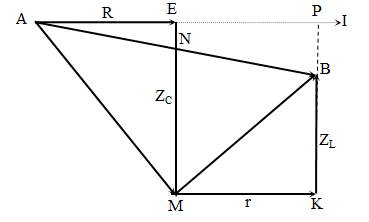
+ $L=C{{\text{R}}^{2}}=C{{\text{r}}^{2}}\to {{R}^{2}}={{r}^{2}}={{Z}_{L}}{{Z}_{C}}\to \dfrac{r}{{{Z}_{L}}}=\dfrac{{{Z}_{C}}}{R}$ Hay $\dfrac{MK}{KB}=\dfrac{ME}{A\text{E}}$ \[\to \Delta AEM\tilde{\ }\Delta BKM\to \] \[\widehat{\text{A}M\text{E}}=\widehat{BMK}\] \[\to \Delta AMB\] vuông tại M → $\tan \widehat{BAM}=\dfrac{MB}{AM}=\dfrac{1}{2}$
+ R = r → AE = EP → N là trung điểm AB → MN = AN = NB \[\to \Delta AMN\] cân tại N → $\widehat{BAM}=\widehat{AM\text{E}}$→ $\tan \widehat{AME}=\dfrac{A\text{E}}{EM}=\dfrac{1}{2}$→$\tan \widehat{EAM}=\dfrac{EM}{A\text{E}}=2$. Lại có $\tan \widehat{IAB}=\tan \left( \widehat{\text{EA}M}-\widehat{\text{BA}M} \right)=\dfrac{\tan \widehat{\text{EA}M}-\tan \widehat{\text{BA}M}}{1+\tan \widehat{\text{EA}M}. \tan \widehat{\text{BA}M}}=\dfrac{2-\dfrac{1}{2}}{1+2. \dfrac{1}{2}}=\dfrac{3}{4}$ \[\to cos\varphi =\]$\cos \widehat{IAB}=0,8$.
Câu 77.
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần, giữa hai điểm M và N chỉ có cuộn dây, giữa 2 điểm N và B chỉ có tụ điện. Đặt vào hai đầu đoạn mạch một điện áp 175 V – 50 Hz thì điện áp hiệu dụng trên đoạn AM là 25 (V), trên đoạn MN là 25 (V) và trên đoạn NB là 175 (V). Tỉ số giữa hệ số công suất của cuộn dây và hệ số công suất của mạch bằng
[A]. $\dfrac{7}{25}$
[B]. $\dfrac{5}{27}$
[C]. $\dfrac{24}{7}$
[D]. $\dfrac{24}{25}$
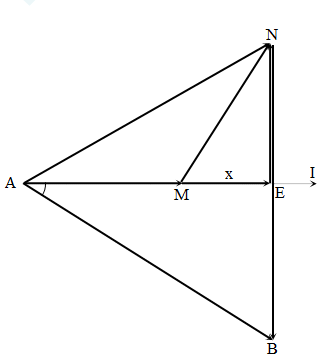
Bài cho: AM = MN = 25 V, AB = NB = 175 V. Đặt ME = x→$NE=\sqrt{{{25}^{2}}-{{x}^{2}}}$ Xét \[\Delta ABE: \] \[A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}}\Rightarrow {{175}^{2}}={{\left( 25+x \right)}^{2}}+{{\left( 175-\sqrt{{{25}^{2}}-{{x}^{2}}} \right)}^{2}}\] → x = 24 V Hệ số công suất cuộn dây: $\cos {{\varphi }_{d}}=\dfrac{ME}{MN}=\dfrac{24}{25}$ Hệ số công suất toàn mạch: $\cos \varphi =\dfrac{AE}{AB}=\dfrac{24+25}{175}=\dfrac{5}{27}$. → $\dfrac{\cos {{\varphi }_{d}}}{\cos \varphi }=\dfrac{24}{7}$ .
Câu 78.
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần \[{{R}_{1}}=50\sqrt{3}\text{ }\Omega \] mắc nối tiếp với tụ điện có điện dung \[C=\dfrac{{{2. 10}^{-4}}}{\pi }F\] , đoạn mạch MB là một cuộn dây. Đặt điện áp xoay chiều \[u=200\sqrt{2}\text{cos(100}\pi \text{t)}\](V) vào hai đầu đoạn mạch AB. Khi đó điện áp trên đoạn mạch MB vuông pha với điện áp trên đoạn mạch AM và có giá trị hiệu dụng \[{{U}_{MB}}=100\sqrt{3}\text{ V}\]. Công suất tiêu thụ trên đoạn mạch AB là
[A]. 100 W.
[B]. 90 W.
[C]. \[100\sqrt{3}\]W.
[D]. 180 W.
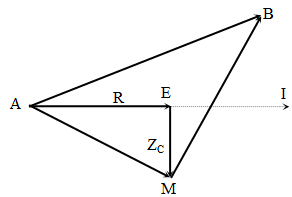
+ $\tan \widehat{\text{EA}M}=\dfrac{{{Z}_{C}}}{R}=\dfrac{1}{\sqrt{3}}\to \widehat{\text{EA}M}={{30}^{0}}$
+ $\sin \widehat{\text{BA}M}=\dfrac{{{U}_{MB}}}{{{U}_{AM}}}=\dfrac{\sqrt{3}}{2}\to \widehat{\text{EA}M}={{60}^{0}}$ \[\to \varphi =\] $\widehat{IAB}={{30}^{0}}$ $U_{AB}^{2}=U_{AM}^{2}+U_{MB}^{2}\to {{U}_{AM}}=100V$ → $I=\dfrac{{{U}_{AM}}}{{{Z}_{AM}}}=\dfrac{{{U}_{AM}}}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=$ 1A \[\to P=UIcos\varphi =\] $100\sqrt{3}$ W.
Câu 79.
Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở R = 25 Ω và tụ điện mắc nối tiếp, đoạn mạch MB chỉ có cuộn dây. Đặt vào hai đầu A, B điện áp xoay chiều có giá trị hiệu dụng 200 V thì thấy điện áp tức thời giữa AM và MB lệch pha $\dfrac{\pi }{3}$ và ${{U}_{AM}}={{U}_{MB}}=\dfrac{2{{U}_{R}}}{\sqrt{3}}$. Công suất tiêu thụ đoạn mạch AB là
[A]. 100 W.
[B]. 200 W.
[C]. 400 W.
[D]. 800 W.
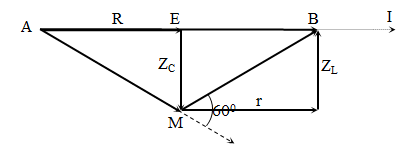
+ $\cos \widehat{EAM}=\dfrac{{{U}_{R}}}{{{U}_{AM}}}=\dfrac{\sqrt{3}}{2}\to \widehat{EAM}={{30}^{0}}$
Dễ thấy $\widehat{EMB}={{60}^{0}}$ mà AM = MB → Mạch có cộng hưởng điện\[\to r=R=25\Omega . \] → $P=\dfrac{{{U}^{2}}}{R+r}=800$W.
Câu 80.
Đoạn mạch AB theo thứ tự gồm các đoạn mạch AM, MN và NB mắc nối tiếp. Đoạn mạch AM chứa R; MN chứa C; NB chứa cuộn dây. Biết điện áp hiệu dụng\[{{U}_{AB}}={{U}_{NB}}=130V\] , \[{{U}_{MB}}=\] $50\sqrt{2}$V, điện áp giữa hai đầu AN và MB vuông pha nhau. Hệ số công suất của đoạn mạch AB là?
[A]. 64 V.
[B]. 56 V.
[C]. 0,923.
[D]. 48 V.
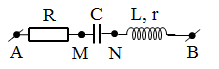
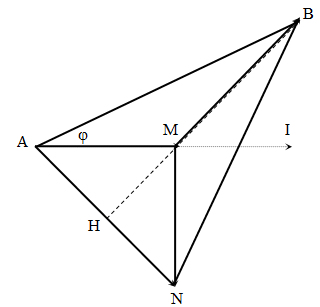
+AB = NB \[\to \Delta ABN\] cân tại B → BH là đường cao → H là trung điểm AN → AMN vuông cân tại M → $\widehat{AMB}={{135}^{0}}$
Áp dụng định lý hàm sin cho \[\Delta ABM\] → $\dfrac{AB}{\sin {{135}^{0}}}=\dfrac{MB}{\sin \varphi }$ hay $\dfrac{130}{\sin {{135}^{0}}}=\dfrac{50\sqrt{2}}{\sin \varphi }$ → $\sin \varphi =\dfrac{5}{13}\to \cos \varphi =\dfrac{12}{13}$ .
Câu 81.
Đoạn mạch AB gồm AN và NB mắc nối tiếp. Đoạn mạch AN gồm điện trở R và cuộn cảm thuần L mắc nối tiếp, đoạn mạch NB chỉ gồm tụ điện C. Đặt vào AB điện áp $u=100\sqrt{2}\cos 100\pi t$(V). Hệ số công suất toàn mạch là 0,6. Hệ số công suất của đoạn mạch AN là 0,8. Điện áp hiệu dụng giữa hai đầu NB là
[A]. 75 V
[B]. 100 V
[C]. 125 V
[D]. 150 V
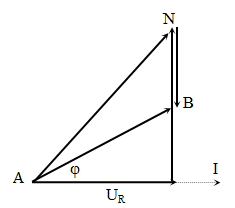
\[cos\varphi =0,6=\] $\dfrac{{{U}_{R}}}{U}\to {{U}_{R}}=60$V. Lại có: \[cos{{\varphi }_{AN}}=0,8=\] $\dfrac{{{U}_{R}}}{{{U}_{AN}}}\to {{U}_{AN}}=75$V = $\sqrt{U_{R}^{2}+U_{L}^{2}}\to {{U}_{L}}=$ 45 $U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=100$ V \[\to {{U}_{C}}=125V. \]
Câu 82.
Đoạn mạch AB gồm AN và NB mắc nối tiếp. Đoạn mạch AN gồm điện trở R và cuộn cảm thuần L mắc nối tiếp, đoạn mạch NB chỉ gồm tụ điện C. Đặt vào AB điện áp $u=120\sqrt{2}\cos 100\pi t$(V) thì thấy điện áp hiệu dụng giữa A,N là 160 V, giữa N,B là 56 V và công suất tiêu thụ trên mạch là 19,2 W. Giá trị R là?
[A]. 280 Ω
[B]. 480 Ω
[C]. 640 Ω
[D]. 720 Ω
$\cos \widehat{ANB}=\dfrac{{{160}^{2}}+{{56}^{2}}-{{120}^{2}}}{2. 160. 56}=0,8\to \sin \widehat{ANB}=0,6=\dfrac{{{U}_{R}}}{{{U}_{AN}}}\to {{U}_{R}}=96$V Mà P = $\dfrac{U_{R}^{2}}{R}$ \[\to R=480\Omega . \].
Câu 83.
Khi xảy ra hiện tượng cộng hưởng trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp thì biểu thức nào sau đây sai?
[A]. cosφ = 1.
[B]. \[{{Z}_{L}}={{Z}_{C. }}\]
[C]. \[{{U}_{L}}={{U}_{R}}\] .
[D]. \[U={{U}_{R}}. \]
Khi xảy ra hiện tượng cộng hưởng trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp thì: \[{{Z}_{L}}={{Z}_{C}},cos\varphi =1,U={{U}_{R}},{{U}_{L}}={{U}_{C}}\] Biểu thức sai là \[{{U}_{L}}={{U}_{R}}\]
Câu 84. ĐH2008
Đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C. Khi dòng điện có tần số góc $\dfrac{1}{\sqrt{LC}}$ chạy qua đoạn mạch thì hệ số công suất đoạn mạch?
[A]. phụ thuộc điện trở thuần của đoạn mạch.
[B]. bằng 0.
[C]. phụ thuộc tổng trở của đoạn mạch.
[D]. bằng 1.
Khi dòng điện có $\omega =\dfrac{1}{\sqrt{LC}}$ Suy ra mạch cộng hưởng $\to \cos \varphi =1$
Câu 85. CĐ2011
Khi nói về hệ số công suất $c\text{os}\varphi $ của đoạn mạch xoay chiều, phát biểu nào sau đây sai?
[A]. Với đoạn mạch chỉ có tụ điện hoặc chỉ có cuộn cảm thuần thì cosφ = 0
[B]. Với đoạn mạch có điện trở thuần thì cosφ = 1
[C]. Với đoạn mạch có R, L, C mắc nối tiếp đang xảy ra cộng hưởng thì cosφ = 0
[D]. Với đoạn mạch gồm tụ điện và điện trở thuần mắc nối tiếp thì $0<c\text{os}\varphi <1$
Với đoạn mạch có R, L, C mắc nối tiếp đang xảy ra cộng hưởng thì \[cos\varphi =1\].
Câu 86.
Mạch điện lần lượt gồm cuộn cảm thuần, tụ điện và điện trở thuần mắc nối tiếp vào hai điểm A, B. Điểm M là điểm nối giữa tụ điện và điện trở thuần. Khi điện áp đặt vào A, B là $u=80\sqrt{2}\cos 100\pi t$(V) thì hệ số công suất trong mạch điện là $\dfrac{\sqrt{2}}{2}$. Khi điện áp tức thời giữa hai đầu điện trở là 48 V thì điện áp tức thời giữa hai điểm A và M có độ lớn là
[A]. 64 V.
[B]. 56 V.
[C]. 102,5 V.
[D]. 48 V.
\[cos\varphi =\] $\dfrac{2}{\sqrt{2}}$ = $\dfrac{{{U}_{0R}}}{{{U}_{0}}}\to {{U}_{0R}}=80$V \[\to {{U}_{0AM}}=80V. \] Ta có: ${{u}_{R}}\bot {{u}_{AM\left( LC \right)}}\to {{\left( \dfrac{{{u}_{R}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{AM}}}{{{U}_{0AM}}} \right)}^{2}}=1$, do đó khi \[{{u}_{R}}=48V\to \left| {{u}_{AM}} \right|=64V\] .
Câu 87.
Đặt điện áp có biểu thức $u=120\sqrt{2}\cos 100\pi t$(V) vào hai đầu đoạn mạch gồm điện trở và tụ điện. Hệ số công suất của đoạn mạch là 0,6. Khi điện áp tức thời giữa hai đầu điện trở là $24\sqrt{2}$V thì điện áp tức thời giữa hai đầu tụ điện có độ lớn bằng
[A]. 95,2 V.
[B]. 98,6 V.
[C]. 128 V.
[D]. 132 V.
\[cos\varphi =0,6=\] $\dfrac{{{U}_{0R}}}{{{U}_{0}}}\to {{U}_{0R}}=72\sqrt{2}$V \[\to {{U}_{0C}}=\] $96\sqrt{2}$V. Ta có: ${{u}_{R}}\bot {{u}_{C}}\to {{\left( \dfrac{{{u}_{R}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{C}}}{{{U}_{0C}}} \right)}^{2}}=1$, do đó khi \[{{u}_{R}}=\] $24\sqrt{2}$V\[\to \left| {{u}_{C}} \right|=128V\] .
Câu 88.
Đoạn mạch AB nối tiếp theo thứ tự gồm: cuộn cảm thuần có độ tự cảm $\dfrac{0,8}{\pi }H$, điện trở R = 40 Ω và tụ điện có điện dung \[\dfrac{{{10}^{-3}}}{2\pi }F\], M là điểm nối giữa cuộn cảm thuần và điện trở, N là điểm nối giữa điện trở và tụ điện. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có điện áp hiệu dụng không đổi, có tần số 50 Hz. Khi điện áp tức thời giữa hai điểm AN là 120 V thì điện áp tức thời giữa hai điểm MB là 80 V. Công suất tiêu thụ điện của đoạn mạch bằng
[A]. 160 W.
[B]. 100 W.
[C]. 120 W.
[D]. 200 W.
Độ lệch pha \[{{u}_{AN}}\] và i là: $\tan \left( {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{R}=2$
Độ lệch pha \[{{u}_{MB}}\] và i là: $\tan \left( {{\varphi }_{{{u}_{MB}}}}-{{\varphi }_{i}} \right)=-\dfrac{{{Z}_{C}}}{R}=-\dfrac{1}{2}$ → $\tan \left( {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}} \right). \tan \left( {{\varphi }_{{{u}_{MB}}}}-{{\varphi }_{i}} \right)=-1\to $${{u}_{AN}}\bot {{u}_{MB}}$
→ \[{{\left( \dfrac{{{u}_{AN}}}{{{U}_{0AN}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{MB}}}{{{U}_{0MB}}} \right)}^{2}}=1\] (*)
Lại có Z = $20\sqrt{13}$Ω, \[{{Z}_{AN}}=\] $40\sqrt{5}\Omega $, \[{{Z}_{MB}}=\] $20\sqrt{5}$
\[\to {{U}_{0AN}}=\] $\dfrac{10}{\sqrt{65}}{{U}_{0}}$ và \[{{U}_{0MB}}=\] $\dfrac{5}{\sqrt{65}}{{U}_{0}}$
Từ (*), ta có: \[{{u}_{AN}}=120V\] và \[{{u}_{MB}}=80V\to {{U}_{0}}=\] $20\sqrt{65}$ V
\[\to U=\] $10\sqrt{130}$ V
\[\to I=\] $\sqrt{\dfrac{5}{2}}$A
\[\to P={{I}^{2}}R=100W. \]