Bài tập tiên đề Bo: về sự hấp thụ và phát xạ photon, vật lí 12 Lượng tử ánh sáng
Lý thuyết cần nhớ để giải bài tập tiên đề bo về sự hấp thụ và bức xạ năng lượng
Mẫu nguyên tử Bo
Mẫu nguyên tử bo là mẫu nguyên tử phù hợp với tiên đề Bo về các trạng thái dừng của nguyên tử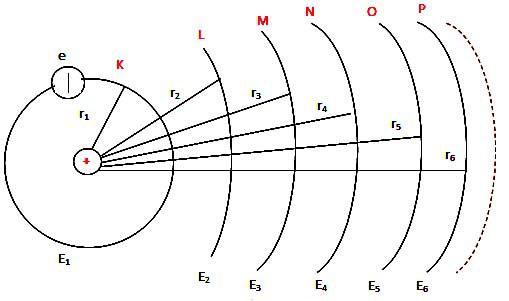
Theo tiên đề Bo về các trạng thái dừng e chuyển động xung quanh hạt nhân ở các quỹ đạo có bán kính xác định các quỹ đạo này sẽ cách hạt nhân một khoảng là r = n2ro
Video Hướng dẫn Bài tập Tiên đề Bo về hấp thụ bức xạ năng lượng
Bài tập tiên đề Bo: về sự hấp thụ phát xạ photon
Câu 1.
Đối với nguyên tử hiđrô, khi êlectron chuyển từ quỹ đạo M về quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng \[0,1026\mu m\]. Năng lượng của phôtôn này bằng
[A]. 1,21 eV
[B]. 11,2 eV.
[C]. 12,1 eV.
[D]. 121 eV.
Khi êlectron chuyển từ quỹ đạo M về quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng \[\lambda =0,1026\mu m\]. Năng lượng của phôtôn này bằng : $\varepsilon =\dfrac{hc}{\lambda }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{0,{{1026. 10}^{-6}}}=1,{{937. 10}^{-18}}\left( J \right)=12,1\left( eV \right)$
Câu 2.
Khi êlectrôn (êlectron) trong nguyên tử hiđrô chuyển từ quĩ đạo dừng có năng lượng \[{{E}_{M}}=-0,85eV\] sang quĩ đạo dừng có năng lượng \[{{E}_{N}}=-13,60eV\] thì nguyên tử phát bức xạ điện từ có bước sóng
[A]. \[0,4340\mu m. \]
[B]. \[0,4860\mu m. \]
[C]. \[0,0974\mu m. \]
[D]. \[0,6563\mu m. \]
Năng lượng của phôtn ánh sáng phát ra khi chuyển từ quỹ đạo M sang quỹ đạo N là: \[\varepsilon =hf={{E}_{M}}{{E}_{N}}=-0,85+13,6=12,75eV=2,{{04. 10}^{-18}}J\] \[\Rightarrow \] $\lambda =\dfrac{hc}{\varepsilon }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{2,{{04. 10}^{-18}}}=0,{{0974. 10}^{-6}}\left( m \right)=0,0974\left( \mu m \right)$
Câu 3.
Khi nguyên tử hiđrô chuyển từ trạng thái dừng có năng lượng -1,514 eV sang trạng thái dừng có năng lượng -3,407 eV thì nguyên tử phát ra bức xạ có tần số
[A]. \[2,{{571. 10}^{13}}Hz. \]
[B]. \[4,{{572. 10}^{14}}Hz. \]
[C]. \[3,{{879. 10}^{14}}Hz. \]
[D]. \[6,{{542. 10}^{12}}Hz. \]
Nguyên tử phát ra một phôtôn có một năng lượng \[\varepsilon =hf={{E}_{cao}}{{E}_{thap}}=-1,524+3,407=1,893eV=3,{{0288. 10}^{-19}}J\] \[\Rightarrow \] f = $f=\dfrac{\varepsilon }{h}=\dfrac{3,{{0288. 10}^{-19}}}{6,{{625. 10}^{-34}}}=4,{{572. 10}^{14}}\left( H\text{z} \right)$
Câu 4.
Đối với nguyên tử hiđrô, các mức năng lượng ứng với các quỹ đạo dừng K, M có giá trị lần lượt là: -13,6 eV; -1,51 eV. Khi êlectron chuyển từ quỹ đạo dừng M về quỹ đạo dừng K, thì nguyên tử hiđrô có thể phát ra bức xạ có bước sóng
[A]. \[102,7\mu m. \]
[B]. 102,7 mm.
[C]. 102,7 nm.
[D]. 102,7 pm.
Khi êlectron chuyển từ quỹ đạo dừng M về quỹ đạo dừng K, Nguyên tử phát ra một phôtôn có một năng lượng là: \[\varepsilon =hf={{E}_{cao}}{{E}_{thap}}=-1,51+13,6=12,09eV=1,{{9344. 10}^{-19}}J\] \[\Rightarrow \] $\lambda =\dfrac{hc}{\varepsilon }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{1,{{9344. 10}^{-19}}}=1,{{027. 10}^{-7}}(m)=102,7\left( nm \right)$
Câu 5.
Nguyên tử hiđtô ở trạng thái cơ bản có mức năng lượng bằng -13,6 eV. Để chuyển lên trạng thái dừng có mức năng lượng -3,4 eV thì nguyên tử hiđrô phải hấp thụ một phôtôn có năng lượng
[A]. 10,2 eV.
[B]. -10,2 eV.
[C]. 17 eV.
[D]. 4 eV.
Nguyên tử phát ra một phôtôn có một năng lượng \[\varepsilon =hf={{E}_{cao}}{{E}_{thap}}=-3,4+13,6=10,2eV\]
Câu 6.
Câu 6 : Khi êlectron ở quỹ đạo dừng K thì năng lượng của nguyên tử hiđrô là –13,6 eV còn khi ở quỹ đạo dừng M thì năng lượng đó là –1,51 eV. Khi êlectron chuyển từ quỹ đạo dừng M về quỹ đạo dừng K thì nguyên tử hiđrô phát ra phôtôn ứng với bức xạ có bước sóng
[A]. 102,7 pm.
[B]. 102,7 mm.
[C]. \[102,7\mu m. \]
[D]. 102,7 nm.
Khi êlectron chuyển từ quỹ đạo dừng M về quỹ đạo dừng K, Nguyên tử phát ra một phôtôn có một năng lượng \[\varepsilon =hf={{E}_{cao}}{{E}_{thap}}=-1,52+13,6=12,09eV=1,{{9344. 10}^{-18}}J\] ⇒ $\lambda =\dfrac{hc}{\varepsilon }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{1,{{9344. 10}^{-18}}}=1,{{027. 10}^{-7}}(m)=102,7(nm)$
Câu 7.
Nguyên tử hiđrô chuyển từ trạng thái dừng có năng lượng \[{{E}_{n}}=-1,5eV\] sang trạng thái dừng có năng lượng \[{{E}_{m}}=-3,4eV\]. Bước sóng của bức xạ mà nguyên tử hiđrô phát ra xấp xỉ bằng
[A]. \[0,{{654. 10}^{-7}}m. \]
[B]. \[0,{{654. 10}^{-6}}m. \]
[C]. \[0,{{654. 10}^{-5}}m. \]
[D]. \[0,{{654. 10}^{-4}}m. \]
Nguyên tử phát ra một phôtôn có một năng lượng \[\varepsilon =hf={{E}_{cao}}{{E}_{thap}}=-1,5+3,4=1,9eV=3,{{04. 10}^{-19}}J\] \[\Rightarrow \] $\lambda =\dfrac{hc}{\varepsilon }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{3,{{04. 10}^{-19}}}=0,{{654. 10}^{-6}}(m)$
Câu 8.
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được tính theo công thức – \[\dfrac{13,6}{{{n}^{2}}}\](eV) (n = 1, 2, 3,…). Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng n = 3 sang quỹ đạo dừng n = 2 thì nguyên tử hiđrô phát ra phôtôn ứng với bức xạ có bước sóng bằng
[A]. \[0,4350\mu m. \]
[B]. \[0,4861\mu m. \]
[C]. \[0,6576\mu m. \]
[D]. \[0,4102\mu m. \]
Nguyên tử phát ra một phôtôn có một năng lượng $\varepsilon =hf={{E}_{3}}-{{E}_{2}}=-\dfrac{13,6}{{{3}^{2}}}+\dfrac{13,6}{{{2}^{2}}}=\dfrac{17}{9}\left( eV \right)=3,{{02. 10}^{-19}}(J)$ \[\Rightarrow \] $\lambda =\dfrac{hc}{\varepsilon }=\dfrac{6,{{625. 10}^{-34}}{{. 3. 10}^{8}}}{3,{{02. 10}^{-19}}}=0,{{6576. 10}^{-6}}(m)=0,6576(\mu m)$
Câu 9.
Theo tiên đề của Bo, khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo L sang quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{21}}\], khi êlectron chuyển từ quỹ đạo M sang quỹ đạo L thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{32}}\] và khi êlectron chuyển từ quỹ đạo M sang quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{31}}\]. Biểu thức xác định \[{{\lambda }_{31}}\] là
[A]. \[{{\lambda }_{31}}=\] \[\dfrac{{{\lambda }_{32}}{{\lambda }_{21}}}{{{\lambda }_{21}}-{{\lambda }_{31}}}\].
[B]. \[{{\lambda }_{31}}={{\lambda }_{32}}-{{\lambda }_{21}}. \]
[C]. \[{{\lambda }_{31}}={{\lambda }_{32}}+{{\lambda }_{21}}. \]
[D]. \[{{\lambda }_{31}}=\]\[\dfrac{{{\lambda }_{32}}{{\lambda }_{21}}}{{{\lambda }_{21}}+{{\lambda }_{31}}}\].
Khi chuyển từ L về K thì photon hấp thụ một năng lượng : \[{{\varepsilon }_{12}}={{E}_{2}}-{{E}_{1}}=\dfrac{hc}{{{\lambda }_{12}}}\] Khi chuyển từ M về L thì photon hấp thụ một năng lượng : ${{\varepsilon }_{32}}={{E}_{3}}-{{E}_{2}}=\dfrac{hc}{{{\lambda }_{32}}}$ Khi chuyển từ M về K thì photon hấp thụ một năng lượng: ${{\varepsilon }_{31}}={{E}_{3}}-{{E}_{1}}={{E}_{3}}-{{E}_{2}}+{{E}_{2}}-{{E}_{1}}=\dfrac{hc}{{{\lambda }_{32}}}+\dfrac{hc}{{{\lambda }_{21}}}\Leftrightarrow \dfrac{hc}{{{\lambda }_{31}}}=\dfrac{hc}{{{\lambda }_{32}}}+\dfrac{hc}{{{\lambda }_{21}}}$ \[\Rightarrow {{\lambda }_{31}}=\dfrac{{{\lambda }_{32}}{{\lambda }_{21}}}{{{\lambda }_{21}}+{{\lambda }_{32}}}\].
Câu 10.
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được xác định bởi công thức ${{E}_{n}}=\dfrac{-13,6}{{{n}^{2}}}$ (eV) (với n = 1, 2, 3,…). Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo N về quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{1}}\]. Khi êlectron chuyển từ quỹ đạo O về quỹ đạo M thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{2}}\]. Mối liên hệ giữa hai bước sóng \[{{\lambda }_{1}}\]và \[{{\lambda }_{2}}\]là
[A]. \[16{{\lambda }_{2}}={{\lambda }_{1}}. \]
[B]. \[256{{\lambda }_{2}}=3375{{\lambda }_{1}}. \]
[C]. \[3375{{\lambda }_{2}}=256{{\lambda }_{1}}. \]
[D]. \[6{{\lambda }_{2}}=5{{\lambda }_{1}}. \]
Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo N về quỹ đạo K ta có: ${{\varepsilon }_{1}}=\dfrac{hc}{{{\lambda }_{1}}}={{E}_{4}}-{{E}_{1}}=\dfrac{-13,6}{{{4}^{2}}}+\dfrac{13,6}{{{1}^{2}}}=12,75\text{e}V$ Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo O về quỹ đạo M ta có: ${{\varepsilon }_{2}}=\dfrac{hc}{{{\lambda }_{2}}}={{E}_{5}}-{{E}_{3}}=\dfrac{-13,6}{{{5}^{2}}}+\dfrac{13,6}{{{3}^{2}}}=\dfrac{1088}{1125}\text{e}V$ \[\Rightarrow \dfrac{{{\varepsilon }_{1}}}{{{\varepsilon }_{2}}}=\dfrac{\dfrac{hc}{{{\lambda }_{1}}}}{\dfrac{hc}{{{\lambda }_{2}}}}=\dfrac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\dfrac{12,75}{\dfrac{1088}{1125}}=\dfrac{3375}{256}\Leftrightarrow 256{{\lambda }_{2}}=3375{{\lambda }_{1}}\]
Câu 11.
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được xác định bởi công thức ${{E}_{n}}=\dfrac{-13,6}{{{n}^{2}}}$ (eV) (với n = 1, 2, 3,…). Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng n = 3 về quỹ đạo dừng n = 1 thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{1}}\]. Khi êlectron chuyển từ quỹ đạo dừng n = 5 về quỹ đạo dừng n = 2 thì nguyên tử phát ra phôtôn có bước sóng \[{{\lambda }_{2}}\]. Mối liên hệ giữa hai bước sóng \[{{\lambda }_{1}}\]và \[{{\lambda }_{2}}\]là
[A]. \[27{{\lambda }_{2}}=128{{\lambda }_{1}}\] .
[B]. \[{{\lambda }_{2}}=5{{\lambda }_{1}}\] .
[C]. \[189{{\lambda }_{2}}=800{{\lambda }_{1}}. \]
[D]. \[{{\lambda }_{2}}=4{{\lambda }_{1}}. \]
Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo n = 3 về quỹ đạo n = 1 ta có: ${{\varepsilon }_{1}}=\dfrac{hc}{{{\lambda }_{1}}}={{E}_{3}}-{{E}_{1}}=\dfrac{-13,6}{{{3}^{2}}}+\dfrac{13,6}{{{1}^{2}}}=\dfrac{544}{45}\text{e}V$ Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo n = 5 về quỹ đạo n = 2 ta có: ${{\varepsilon }_{2}}=\dfrac{hc}{{{\lambda }_{2}}}={{E}_{5}}-{{E}_{2}}=\dfrac{-13,6}{{{5}^{2}}}+\dfrac{13,6}{{{2}^{2}}}=\dfrac{357}{125}\text{e}V$ \[\Rightarrow \dfrac{{{\varepsilon }_{1}}}{{{\varepsilon }_{2}}}=\dfrac{\dfrac{hc}{{{\lambda }_{1}}}}{\dfrac{hc}{{{\lambda }_{2}}}}=\dfrac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\dfrac{\dfrac{544}{45}}{\dfrac{357}{125}}=\dfrac{800}{189}\Leftrightarrow 189{{\lambda }_{2}}=800{{\lambda }_{1}}\]
Câu 12.
Theo mẫu nguyên tử Bo, trong nguyên tử hidrô, khi êlectron chuyển từ quỹ đạo P về quỹ đạo K thì nguyên tử phát ra phôton ứng với bức xạ có tần số \[{{f}_{1}}\]. Khi êlectron chuyển từ quỹ đạo P về quỹ đạo L thì nguyên tử phát ra phôtôn ứng với bức xạ có tần số \[{{f}_{2}}\]. Nếu êlectron chuyển từ quỹ đạo L về quỹ đạo K thì nguyên tử phát ra phôtôn ứng với bức xạ có tần số
[A]. \[{{f}_{3}}={{f}_{1}}{{f}_{2}}\]
[B]. \[{{f}_{3}}={{f}_{1}}+{{f}_{2}}\]
[C]. \[{{\text{f}}_{\text{3}}}=\text{ }\sqrt{{{\text{f}}_{\text{1}}}^{2}\text{+ }{{\text{f}}_{\text{2}}}^{2}}\]
[D]. \[{{f}_{3}}=\dfrac{{{f}_{1}}{{f}_{2}}}{{{f}_{1}}+{{f}_{2}}}\]
Khi êlectron chuyển từ quỹ đạo P về quỹ đạo K thì nguyên tử phát ra phôton có năng lượng: ${{\varepsilon }_{1}}=h{{f}_{1}}={{E}_{6}}-{{E}_{1}}$ Khi êlectron chuyển từ quỹ đạo P về quỹ đạo L thì nguyên tử phát ra phôtôn có năng lượng: ${{\varepsilon }_{2}}=h{{f}_{2}}={{E}_{6}}-{{E}_{2}}$ Nếu êlectron chuyển từ quỹ đạo L về quỹ đạo K thì nguyên tử phát ra phôtôn có năng lượng: ${{\varepsilon }_{3}}=h{{f}_{3}}={{E}_{2}}-{{E}_{1}}={{E}_{2}}-{{E}_{6}}+{{E}_{6}}-{{E}_{1}}=-h{{f}_{2}}+h{{f}_{1}}$ $\Leftrightarrow {{f}_{3}}={{f}_{1}}-{{f}_{2}}$
Câu 13.
Mức năng lượng \[{{E}_{n}}\] trong nguyên tử hiđrô được xác định \[{{E}_{n}}=-\dfrac{{{E}_{0}}}{{{n}^{2}}}\] (trong đó n là số nguyên dương, \[{{E}_{0}}\] là năng lượng ứng với trạng thái cơ bản). Khi e nhảy từ quỹ đạo thứ ba về quỹ đạo thứ hai thì nguyên tử hiđrô phát ra bức xạ có bước sóng \[{{\lambda }_{0}}\]. Nếu êlectron nhảy từ quỹ đạo thứ hai về quỹ đạo thứ nhất thì bước sóng của bức xạ được phát ra sẽ là:
[A]. $\dfrac{{{\lambda }_{0}}}{15}$
[B]. $\dfrac{5{{\lambda }_{0}}}{7}$
[C]. \[{{\lambda }_{0}}\]
[D]. $\dfrac{5{{\lambda }_{0}}}{27}$.
Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo n = 3 về quỹ đạo n = 2 ta có: ${{\varepsilon }_{1}}=\dfrac{hc}{{{\lambda }_{0}}}={{E}_{3}}-{{E}_{2}}=-\dfrac{{{E}_{0}}}{{{3}^{2}}}+\dfrac{{{E}_{0}}}{{{2}^{2}}}=\dfrac{5{{E}_{0}}}{36}\Rightarrow {{E}_{0}}=\dfrac{36hc}{5{{\lambda }_{0}}}$ Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo n = 2 về quỹ đạo n = 1 ta có: ${{\varepsilon }_{2}}=\dfrac{hc}{\lambda }={{E}_{2}}-{{E}_{1}}=-\dfrac{{{E}_{0}}}{{{2}^{2}}}+\dfrac{{{E}_{0}}}{{{1}^{2}}}=\dfrac{3{{E}_{0}}}{4}=\dfrac{3}{4}. \dfrac{36hc}{5{{\lambda }_{0}}}=\dfrac{27hc}{5{{\lambda }_{0}}}$ $\Leftrightarrow \lambda =\dfrac{5}{27}{{\lambda }_{0}}$
Câu 14.
Để chuyển êlectron từ quỹ đạo K lên M; L lên N; L lên M thì nguyên tử hiđrô cần hấp thụ phôtôn mang năng lượng lần lượt là 12,09 MeV; 2,55 MeV; 1,89 MeV. Nguyên tử hiđrô phải hấp thụ phôtôn mang năng lượng bao nhiêu để chuyển êlectron từ quỹ đạo K lên N ?
[A]. 11,34 MeV.
[B]. 16,53 MeV.
[C]. 12,75 MeV.
[D]. 9,54 MeV.
Hướng dẫn giải bài tập tiên đề BO
$\left. \begin{align} & {{\varepsilon }_{1}}={{E}_{M}}-{{E}_{K}}=12,09 \\ & {{\varepsilon }_{2}}={{E}_{N}}-{{E}_{L}}=2,55 \\ & {{\varepsilon }_{3}}={{E}_{M}}-{{E}_{L}}=1,89 \\ \end{align} \right|$ $\Rightarrow {{\varepsilon }_{4}}={{E}_{N}}-{{E}_{K}}={{E}_{N}}-{{E}_{L}}-\left( {{E}_{M}}-{{E}_{L}} \right)+{{E}_{M}}-{{E}_{K}}=2,55-1,89+12,09=12,75(MeV)$
Câu 15.
Gọi \[{{E}_{n}}\] là mức năng lượng của nguyên từ hidro ở trạng thái năng lượng ứng với quỹ đạo n (n > 1). Khi electron chuyển về các quỹ đạo bên trong thì có thể phát ra số bức xạ là:
[A]. n!
[B]. (n – 1)!
[C]. n(n – 1)
[D]. 0,5. n(n – 1)
Hướng dẫn giải bài tập tiên đề BO
Gọi \[{{E}_{n}}\] là mức năng lượng của nguyên từ hidro ở trạng thái năng lượng ứng với quỹ đạo n (n > 1). Khi electron chuyển về các quỹ đạo bên trong thì có thể phát ra số bức xạ là: 0,5. n(n – 1)
Câu 16.
Nguyên tử Hiđrô bị kích thích do chiếu xạ và electrôn của nguyên tử đã chuyển từ quỹ đạo K lên N. Sau khi ngừng chiếu xạ, nguyên tử Hiđrô phát xạ thứ cấp, phổ xạ này gồm
[A]. hai vạch.
[B]. ba vạch.
[C]. bốn vạch.
[D]. sáu vạch.
Hướng dẫn giải bài tập tiên đề BO
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là: 0,5. n(n – 1) Khi electrôn chuyển từ quỹ đạo N (có n = 4) vào quỹ đạo bên trong thì số bức xạ thứ cấp là: 0,5. 4(4 – 1) = 6
Câu 17.
Hãy xác định trạng thái kích thích cao nhất của các nguyên tử hiđrô trong trường hợp người ta chỉ thu được 6 vạch quang phổ phát xạ của nguyên tử hiđrô
[A]. Trạng thái L
[B]. Trạng thái M
[C]. Trạng thái N
[D]. Trạng thái O
Hướng dẫn giải bài tập tiên đề BO
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là: \[0,5. n\left( n-1 \right)=6\Leftrightarrow n=4\] Trạng thái kích thích cao nhất ứng với quỹ đạo có n = 4 là quỹ đạo N
Câu 18.
Một đám nguyên tử hiđrô đang ở trạng thái kích thích mà êlectron chuyển động trên quỹ đạo dừng N. Khi êlectron chuyển về các quỹ đạo dừng bên trong thì quang phổ vạch phát xạ của đám nguyên tử đó có bao nhiêu vạch?
[A]. 3.
[B]. 1.
[C]. 6.
[D]. 4.
Hướng dẫn giải bài tập tiên đề BO
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là: 0,5. n(n – 1) Khi electrôn chuyển từ quỹ đạo N (có n = 4) vào quỹ đạo bên trong thì số bức xạ thứ cấp là: 0,5. 4(4 – 1) = 6
Câu 19.
Các nguyên tử hiđrô đang ở trạng thái dừng ứng với êlectron chuyển động trên quỹ đạo có bán kính lớn gấp 9 lần so với bán kính Bo. Khi chuyển về các trạng thái dừng có năng lượng thấp hơn thì các nguyên tử sẽ phát ra các bức xạ có tần số khác nhau. Có thể có nhiều nhất bao nhiêu tần số?
[A]. 4.
[B]. 2.
[C]. 3.
[D]. 1.
Hướng dẫn giải bài tập tiên đề BO
+ Bán kính quỹ đạo dứng là: \[r={{n}^{2}}{{r}_{0}}=9{{r}_{0}}\Rightarrow n=3\] + Khi chuyển về các trạng thái dừng có năng lượng thấp hơn thì các nguyên tử sẽ phát ra các bức xạ có tần số khác nhau. Có thể có nhiều nhất : 0,5. 3(3 – 1) = 3
Câu 20.
Chùm nguyên tử Hiđrô đang ở trạng thái cơ bản, bị kích thích phát sáng thì chúng có thể phát ra tối đa 3 vạch quang phổ. Khi bị kích thích electron trong nguyên tử H đã chuyển sang quỹ đạo?
[A]. M.
[B]. L.
[C]. O.
[D]. N.
Hướng dẫn giải bài tập tiên đề BO
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là: \[0,5. n\left( n-1 \right)=3\Leftrightarrow n=3\] Trạng thái kích thích cao nhất ứng với quỹ đạo có n = 3 là quỹ đạo M
Câu 21.
Một nguyên tử hiđrô đang ở trạng thái cơ bản, hấp thụ một phôtôn có năng lượng \[{{\varepsilon }_{0}}\] và chuyển lên trạng thái dừng ứng với quỹ đạo N của êlectron. Từ trạng thái này, nguyên tử chuyển về các trạng thái dừng có mức năng lượng thấp hơn thì có thể phát ra phôtôn có năng lượng lớn nhất là
[A]. \[3{{\varepsilon }_{0}}. \]
[B]. \[2{{\varepsilon }_{0}}. \]
[C]. \[4{{\varepsilon }_{0}}. \]
[D]. \[{{\varepsilon }_{0}}. \]
Hướng dẫn giải bài tập tiên đề BO
Một nguyên tử hiđrô đang ở trạng thái cơ bản, hấp thụ một phôtôn có năng lượng \[{{\varepsilon }_{0}}\] và chuyển lên trạng thái dừng ứng với quỹ đạo N của êlectron. Từ trạng thái này, nguyên tử chuyển về các trạng thái dừng có mức năng lượng thấp hơn thì có thể phát ra phôtôn có năng lượng lớn nhất là \[{{\varepsilon }_{0}}\] (chính bằng năng lượng từ quỹ đạo N để chuyển về trạng thái cơ bản)
Câu 22.
Năng lượng của nguyên tử hiđrô cho bởi biểu thức ${{E}_{n}}=\dfrac{-13,6}{{{n}^{2}}}$ eV (n = 1, 2, 3… ). Chiếu vào đám khí hiđrô ở trạng thái cơ bản bức xạ điện từ có tần số f, sau đó đám khí phát ra 6 bức xạ có bước sóng khác nhau. Tần số f là:
[A]. \[1,{{92. 10}^{-34}}Hz\]
[B]. \[3,{{08. 10}^{9}}MHz\]
[C]. \[3,{{08. 10}^{-15}}Hz\]
[D]. \[1,{{92. 10}^{28}}MHz\]
Hướng dẫn giải bài tập tiên đề BO
Chiếu vào đám khí hiđrô ở trạng thái cơ bản bức xạ điện từ có tần số f, sau đó đám khí phát ra 6 bức xạ có bước sóng khác nhau \[\Rightarrow 0,5. n\left( n-1 \right)=6\Rightarrow n=4\Rightarrow \] Trạng thái N Vậy năng lượng mà photon đã hấp thụ là : \[{{\varepsilon }_{2}}=-\dfrac{13,6}{{{4}^{2}}}+\dfrac{13,6}{{{1}^{2}}}=12,75\left( eV \right)=hf\] $\Rightarrow f=\dfrac{\varepsilon }{h}=\dfrac{12,75. 1,{{6. 10}^{-19}}}{6,{{625. 10}^{-34}}}=3,{{08. 10}^{15}}\left( H\text{z} \right)=3,{{08. 10}^{9}}\left( MH\text{z} \right)$
Câu 23.
Khi elêctrôn ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được xác định bởi ${{E}_{n}}=\dfrac{-13,6}{{{n}^{2}}}$(eV) với n = 1, 2, 3,… Một đám khí hiđrô hấp thụ năng lượng chuyển lên trạng thái dừng có năng lượng cao nhất là ${{E}_{3}}$ (ứng với quỹ đạo M). Tỉ số giữa bước sóng dài nhất và ngắn nhất mà đám khí trên có thể phát ra là
[A]. $\dfrac{27}{8}$.
[B]. $\dfrac{32}{5}$.
[C]. $\dfrac{32}{27}$.
[D]. $\dfrac{32}{3}$.
Hướng dẫn giải bài tập tiên đề BO
\[\dfrac{hc}{{{\lambda }_{\min }}}={{E}_{M}}-{{E}_{K}}={{E}_{3}}-{{E}_{1}}=13,6\left( 1-\dfrac{1}{9} \right)=\dfrac{544}{45}\] \[\dfrac{hc}{{{\lambda }_{\text{max}}}}={{E}_{M}}-{{E}_{L}}={{E}_{3}}-{{E}_{2}}=13,6\left( \dfrac{1}{4}-\dfrac{1}{9} \right)=\dfrac{17}{9}\] \[\Rightarrow \dfrac{{{\lambda }_{\max }}}{{{\lambda }_{\min }}}=\dfrac{\dfrac{544}{45}}{\dfrac{17}{9}}=\dfrac{32}{5}\]
Câu 24.
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được xác định bởi công thức ${{E}_{n}}=\dfrac{-A}{{{n}^{2}}}$ (eV) (với n = 1, 2, 3,…). , trong đó A là hằng số dương. Khi nguyên tử đang ở trạng thái cơ bản thì bị kích thích bởi điện trường mạnh và làm cho nguyên tử có thể phát ra tối đa 10 bức xạ. Hỏi trong các bức xạ mà nguyên tử hiđrô có thể phát ra trong trường hợp này thì tỉ số về bước sóng giữa bức xạ dài nhất và ngắn nhất là bao nhiêu?
[A]. 79,5
[B]. 128/3
[C]. 32/25
[D]. 6
Hướng dẫn giải bài tập tiên đề BO
Khi nguyên tử đang ở trạng thái cơ bản thì bị kích thích bởi điện trường mạnh và làm cho nguyên tử có thể phát ra tối đa 10 bức xạ \[\Rightarrow 0,5. n\left( n-1 \right)=10\Rightarrow n=5\Rightarrow \] Quỹ đạo O \[\dfrac{hc}{{{\lambda }_{\min }}}={{E}_{O}}-{{E}_{K}}={{E}_{5}}-{{E}_{1}}=A\left( 1-\dfrac{1}{25} \right)=\dfrac{24}{25}A\] \[\dfrac{hc}{{{\lambda }_{\text{max}}}}={{E}_{O}}-{{E}_{N}}={{E}_{5}}-{{E}_{4}}=A\left( \dfrac{1}{16}-\dfrac{1}{25} \right)=\dfrac{9}{400}A\] \[\Rightarrow \dfrac{{{\lambda }_{\max }}}{{{\lambda }_{\min }}}=\dfrac{\dfrac{24}{25}A}{\dfrac{9}{400}A}=\dfrac{128}{3}\]
Câu 25.
Kích thích cho các nguyên tử H chuyển từ trạng thái cơ bản lên trạng thái kích thích sao cho bán kính quỹ đạo tăng 9 lần. Trong các bức xạ nguyên tử hiđrô phát ra sau đó, tỉ số giữa bước sóng dài nhất và bước sóng ngắn nhất là:
[A]. 32/27
[B]. 32/37
[C]. $\dfrac{32}{5}$
[D]. 9/8
Hướng dẫn giải bài tập tiên đề BO
Khi nguyên tử H ở trạng thái cơ bản thì bán kính quỹ đạo là: ${{r}_{0}}$ Sau khi bị kích thích nguyên tử chuyển lên quỹ đạo có bán kính: $9{{r}_{0}}\Rightarrow {{n}^{2}}{{r}_{0}}=9{{r}_{0}}\Rightarrow n=3$ $\Rightarrow $ Quỹ đạo M \[\dfrac{hc}{{{\lambda }_{\min }}}={{E}_{M}}-{{E}_{K}}={{E}_{3}}-{{E}_{1}}=13,6\left( 1-\dfrac{1}{9} \right)=\dfrac{544}{45}\] \[\dfrac{hc}{{{\lambda }_{\text{max}}}}={{E}_{M}}-{{E}_{L}}={{E}_{3}}-{{E}_{2}}=13,6\left( \dfrac{1}{4}-\dfrac{1}{9} \right)=\dfrac{17}{9}\] \[\Rightarrow \dfrac{{{\lambda }_{\max }}}{{{\lambda }_{\min }}}=\dfrac{\dfrac{544}{45}}{\dfrac{17}{9}}=\dfrac{32}{5}\]
Câu 26.
Mức năng lượng của nguyên tử hiđrô có biểu thức: ${{E}_{n}}=-\dfrac{13,6}{{{n}^{2}}}\left( eV \right)$; n = 1, 2, 3…. Kích thích nguyên tử hiđrô ở trạng thái cơ bản bằng cách cho hấp thụ một phôtôn có năng lượng thích hợp thì bán kính quĩ đạo dừng của êlectrôn tăng lên 25 lần. Bước sóng lớn nhất của bức xạ mà nguyên tử hiđrô có thể phát ra sau đó là:
[A]. \[5,2\mu m\]
[B]. \[0,4\mu m\]
[C]. \[3\mu m\]
[D]. \[4\mu m\]
Hướng dẫn giải bài tập tiên đề BO
Khi nguyên tử H ở trạng thái cơ bản thì bán kính quỹ đạo là: ${{r}_{0}}$ Sau khi bị kích thích nguyên tử chuyển lên quỹ đạo có bán kính: $25{{r}_{0}}\Rightarrow {{n}^{2}}{{r}_{0}}=25{{r}_{0}}\Rightarrow n=5$ $\Rightarrow $ Quỹ đạo O \[\dfrac{hc}{{{\lambda }_{\text{max}}}}={{E}_{O}}-{{E}_{N}}={{E}_{5}}-{{E}_{4}}=-13,6\left( \dfrac{1}{25}-\dfrac{1}{16} \right)=\dfrac{153}{500}eV\] $\Rightarrow {{\lambda }_{\max }}=0,4\mu m$
Câu 27.
Năng lượng của nguyên tử Hiđrô được xác định: \[{{E}_{n}}=-\dfrac{13,6}{{{n}^{2}}}(eV)\] ( n = 1, 2, 3… ). Khi cung cấp cho nguyên tử Hiđrô ở trạng thái cơ bản các phôtôn có năng lượng 10,5 eV và 12,75 eV thì nguyên tử hấp thụ được phôtôn có năng lượng:
[A]. 10,5 eV và chuyển đến quỹ đạo L.
[B]. 12,75 eV và chuyển đến quỹ đạo M.
[C]. 10,5 eV và chuyển đến quỹ đạo M.
[D]. 12,75 eV và chuyển đến quỹ đạo N.
Hướng dẫn giải bài tập tiên đề BO
+ Nếu nguyên tử hấp thụ phôtôn có năng lượng 10,5 eV: ${{E}_{n}}-{{E}_{0}}=10,5\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+13,6=10,5\Rightarrow n=2,09$ (loại) + Nếu nguyên tử hấp thụ phôtôn có năng lượng 12,75 eV: ${{E}_{n}}-{{E}_{0}}=10,5\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+13,6=12,75\Rightarrow n=4$ (thỏa mãn) $\Rightarrow $ Quỹ đạo N
Câu 28.
Một đám nguyên tử hiđrô đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số \[{{f}_{1}}\] vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ. Khi chiếu bức xạ có tần số \[{{f}_{2}}\] vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ. Biết năng lượng ứng với các trạng thái dừng của nguyên tử hiđrô được tính theo biểu thức \[{{E}_{n}}=-\dfrac{{{E}_{0}}}{{{n}^{2}}}\] (\[{{E}_{0}}\] là hằng số dương, n = 1, 2, 3,… ). Tỉ số $\dfrac{{{f}_{1}}}{{{f}_{2}}}$ là
[A]. $\dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{3}{10}$
[B]. $\dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{10}{3}$
[C]. $\dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{25}{27}$
[D]. $\dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{128}{135}$
Hướng dẫn giải bài tập tiên đề BO
Khi chiếu bức xạ có tần số \[{{f}_{1}}\] vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ \[\Rightarrow 0,5. n\left( n-1 \right)=3\Rightarrow n=3\Rightarrow \]Quỹ đạo M Khi chiếu bức xạ có tần số \[{{f}_{2}}\] vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ \[\Rightarrow 0,5. n\left( n-1 \right)=10\Rightarrow n=5\Rightarrow \]Quỹ đạo O $\Rightarrow \dfrac{h{{f}_{1}}}{h{{f}_{2}}}=\dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{{{E}_{3}}-{{E}_{0}}}{{{E}_{5}}-{{E}_{0}}}=\dfrac{25}{27}$
Câu 29.
Khi chiếu lần lượt các bức xạ đơn sắc có các phôtôn mang năng lượng tương ứng là 10,200 eV, 12,750 eV, 13,060 eV vào nguyên tử hiđrô ở trạng thái cơ bản. Biết các mức năng lượng của nguyên tử hiđrô ở trạng thái dừng được xác định bằng các công thức: \[{{E}_{n}}=-\dfrac{13,6}{{{n}^{2}}}eV\]với n = 1,2,3… Nguyên tử hiđrô đó có thể hấp thụ bao nhiêu loại phôtôn trong các chùm trên ?
[A]. 2.
[B]. 1.
[C]. 3.
[D]. 0.
Hướng dẫn giải bài tập tiên đề BO
+ Nếu nguyên tử hấp thụ phôtôn có năng lượng 10,2 eV: ${{E}_{n}}-{{E}_{0}}=10,2\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+13,6=10,2\Rightarrow n=2$ (thỏa mãn) + Nếu nguyên tử hấp thụ phôtôn có năng lượng 12,75 eV: ${{E}_{n}}-{{E}_{0}}=10,5\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+13,6=12,75\Rightarrow n=4$ (thỏa mãn) + Nếu nguyên tử hấp thụ phôtôn có năng lượng 13,06 eV: ${{E}_{n}}-{{E}_{0}}=10,5\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+13,6=13,06\Rightarrow n=5,02$ (loại) $\Rightarrow $ Nguyên tử hiđrô đó có thể hấp thụ 2 loại phôtôn trong các chùm trên.
Câu 30.
Các mức năng lượng của các trạng thái dừng của nguyên tử hidro được xác định bằng biểu thức \[{{E}_{n}}=-\dfrac{13,6}{{{n}^{2}}}eV\](n = 1, 2, 3,…). Nếu nguyên tử hidro hấp thụ một photon có năng lượng 2,55eV thì bước sóng nhỏ nhất của bức xạ mà nguyên tử hidro có thể phát ra là:
[A]. \[9,{{74. 10}^{-8}}m\]
[B]. \[1,{{46. 10}^{-8}}m\]
[C]. \[1,{{22. 10}^{-8}}m\]
[D]. \[4,{{87. 10}^{-8}}m. \]
Hướng dẫn giải bài tập tiên đề BO
Khi nguyên tử hidro hấp thụ một photon có năng lượng 2,55eV: $\Rightarrow {{E}_{n}}-{{E}_{m}}=2,55eV\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+\dfrac{13,6}{{{m}^{2}}}=2,55\Rightarrow \dfrac{1}{{{m}^{2}}}-\dfrac{1}{{{n}^{2}}}=\dfrac{3}{16}$ $\Rightarrow \left\{ \begin{align} & m=2 \\ & n=4 \\ \end{align} \right. $ Khi đó nguyên tử chuyển từ quỹ đạo L lên quỹ đạo N. Sau đó bước sóng nhỏ nhất của bức xạ mà nguyên tử hidro có thể phát ra là: \[\dfrac{hc}{{{\lambda }_{\min }}}={{E}_{N}}-{{E}_{K}}={{E}_{4}}-{{E}_{1}}=13,6\left( 1-\dfrac{1}{16} \right)=12,75eV\] $\Rightarrow {{\lambda }_{\min }}=9,{{74. 10}^{-8}}m$
Câu 31.
Các mức năng lượng của các trạng thái dừng của nguyên tử hiđrô được xác định bằng biểu thức ${{E}_{n}}=-\dfrac{13,6}{{{n}^{2}}}$ (eV) (n = 1, 2, 3,…). Nếu nguyên tử hiđrô hấp thụ một phôtôn có năng lượng 2,856 eV thì sau đó tần số lớn nhất của bức xạ mà nguyên tử hiđrô đó có thể phát ra là
[A]. \[3,{{15. 10}^{12}}kHz. \]
[B]. \[6,{{9. 10}^{14}}Hz. \]
[C]. \[2,{{63. 10}^{15}}Hz. \]
[D]. \[1,{{8. 10}^{13}}kHz. \]
Khi nguyên tử hidro hấp thụ một photon có năng lượng 2,856eV: $\Rightarrow {{E}_{n}}-{{E}_{m}}=2,856eV\Rightarrow -\dfrac{13,6}{{{n}^{2}}}+\dfrac{13,6}{{{m}^{2}}}=2,856\Rightarrow \dfrac{1}{{{m}^{2}}}-\dfrac{1}{{{n}^{2}}}=\dfrac{21}{100}$ $\Rightarrow \left\{ \begin{align} & m=2 \\ & n=5 \\ \end{align} \right. $ Khi đó nguyên tử chuyển từ quỹ đạo L lên quỹ đạo O. Sau đó tần số lớn nhất của bức xạ mà nguyên tử hiđrô đó có thể phát ra là: $h{{f}_{\max }}={{E}_{O}}-{{E}_{K}}={{E}_{5}}-{{E}_{1}}=13,6(1-\dfrac{1}{25})=13,056eV$ $\Rightarrow {{f}_{\max }}=3,{{15. 10}^{15}}Hz=3,{{15. 10}^{12}}kHz$