Bài toán phương trình dao động của các điểm trên dây có sóng dừng
Câu 1.
Trên dây có sóng dừng hai đầu cố định, biên độ dao động của phần tử trên dây tại bụng sóng là \[2a\], bước sóng λ. Tại một điểm trên dây có vị trí cân bằng cách một nút một đoạn \[\dfrac{\lambda }{12}\] có biên độ dao động là:
[A]. $\dfrac{a}{2}$
[B]. \[a\sqrt{2}. \]
[C]. \[a\sqrt{3}. \]
[D]. \[a. \]
Điểm có VTCB cách nút một đoạn x = $\dfrac{\lambda }{2}$ nên ${{A}_{M}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|=2a\left| \sin \dfrac{2\pi \dfrac{\lambda }{12}}{\lambda } \right|=a$
Câu 2.
Trên dây có sóng dừng hai đầu cố định, biên độ dao động của phần tử trên dây tại bụng sóng là \[2a\], bước sóng λ. Tại một điểm trên dây có vị trí cân bằng cách vị trí cân bằng một bụng một đoạn \[\dfrac{\lambda }{6}\] có biên độ dao động là:
[A]. $\dfrac{a}{2}$
[B]. \[a\sqrt{2}. \]
[C]. \[a\sqrt{3}. \]
[D]. \[a. \]
Điểm có VTCB cách VTCB của 1 bụng đoạn x = $\dfrac{\lambda }{6}$ $\Rightarrow {{A}_{M}}={{A}_{b}}. \left| \cos \dfrac{2\pi x}{\lambda } \right|=2a\left| \cos \dfrac{2\pi \dfrac{\lambda }{6}}{\lambda } \right|=a$
Câu 3.
Trên dây có sóng dừng hai đầu cố định, biên độ dao động của phần tử trên dây tại bụng sóng là \[2a\]. A là nút, B là vị trí cân bằng của điểm bụng gần A nhất. Điểm C trên dây có vị trí cân bằng là trung điểm của AB dao động với biên độ là
[A]. $\dfrac{a}{2}$
[B]. \[a\sqrt{2}. \]
[C]. \[a\sqrt{3}. \]
[D]. \[a. \]
A là nút, B bụng gần A nhất nên .. (C là trung điểm AB) $\Rightarrow {{A}_{C}}={{A}_{B}}. \left| \sin \dfrac{2\pi AC}{\lambda } \right|=a\sqrt{2}$
Câu 4.
Trên dây có sóng dừng hai đầu cố định, biên độ dao động của phần tử trên dây tại bụng sóng là \[2a\]. A là nút, B là vị trí cân bằng của điểm bụng gần A nhất. Điểm trên dây có vị trí cân bằng C nằm giữa A và B, AC = 2CB dao động với biên độ là
[A]. $\dfrac{a}{2}$
[B]. \[a\sqrt{2}. \]
[C]. \[a\sqrt{3}. \]
[D]. \[a. \]
Ta có AB = $\dfrac{\lambda }{4}$ mà AC = 2CB (C nằm giữa AB) Þ AC = $\dfrac{2}{3}AB=\dfrac{\lambda }{6}\Rightarrow {{A}_{C}}={{A}_{b}}. \left| \sin \dfrac{2\pi AC}{\lambda } \right|=a\sqrt{3}$
Câu 5.
Một sợi dây AB có chiều dài 1 m căng ngang, đầu A cố định, đầu B gắn với một nhánh của âm thoa. Trên dây AB có một sóng dừng ổn định với 4 bụng sóng, biên độ bụng sóng là 2 cm, B được coi là nút sóng. Điểm trên dây có vị trí cân bằng cách A một đoạn \[\dfrac{13}{24}\]m dao động với biên độ là
[A]. 1 cm
[B]. 2 cm
[C]. \[\sqrt{2}. \]
[D]. \[\sqrt{3}. \].
Dây cố định 2 đầu có 4 bụng nên $\ell =4\dfrac{\lambda }{2}=1(m)\Rightarrow \lambda =0,5m$ Điểm trên dây có VTCB cách nút A : x = $\dfrac{13}{24}m$ suy ra biên độ ${{A}_{M}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|=2\left| \sin \dfrac{2\pi \dfrac{13}{24}}{0. 5} \right|=1(cm)$
Câu 6.
Không xét các điểm bụng hoặc nút, quan sát thấy những điểm có cùng biên độ và ở gần nhau nhất thì đều cách đều nhau 15cm. Bước sóng trên dây có giá trị bằng
[A]. 30 cm.
[B]. 60 cm.
[C]. 90 cm.
[D]. 45 cm.
Các điểm có cùng biên độ đều cách đều nhau thì cách nhau một khoảng λ/4 =15cm. Vậy \[\lambda =60\]cm
Câu 7.
Sóng dừng trên sợi dây đàn hồi căng ngang hai đầu cố định dài 1,2 m. Không xét các điểm bụng hoặc nút, trên dây có ba điểm liên tiếp M, N, P dao động cùng biên độ, MN = NP = 10 cm. Số điểm nút trên dây là
[A]. 9.
[B]. 6.
[C]. 8.
[D]. 7.
M, N, P là 3 điểm liên tiếp dao động cùng biên độ (không phải nút, bụng) → MN + NP =$\dfrac{\lambda }{2}$
$\Rightarrow \dfrac{\lambda }{2}=20cm=0. 2m\Rightarrow k=\dfrac{l}{\dfrac{\lambda }{2}}=\dfrac{1. 2}{0. 2}=6$ .
Vậy có 6 bụng và 7 nút.
Câu 8.
Một sợi dây đàn hồi đang có sóng dừng. Trên dây, những điểm dao động với cùng biên độ A1 có vị trí cân bằng liên tiếp cách đều nhau một đoạn d1 và những điểm dao động với cùng biên độ A2 có vị trí cân bằng liên tiếp cách đều nhau một đoạn d2. Biết A1 > A2 > 0. Biểu thức nào sau đây đúng?
[A]. d1 = 0,5d2.
[B]. d1 = 4d2.
[C]. d1 = 0,25d2.
[D]. d1 = 2d2.
Do A1 > A2 > 0 ta bỏ qua vị trí nút vậy chỉ còn lại 2 trường hợp còn lại tương ứng với A1 và A2 là bụng và điểm giữa bụng và nút.
Suy ra A1 = Ab (biên độ tại bụng)
→ d1 = $\dfrac{\lambda }{2}$ .
Còn lại với A2, ta có: vì các điểm dao động cùng biên độ liên tiếp nhau tương tự câu 7:
${{d}_{2}}+{{d}_{2}}=\dfrac{\lambda }{2}\Rightarrow {{d}_{2}}=\dfrac{\lambda }{4}\Rightarrow {{d}_{1}}=2{{d}_{2}}$
Câu 9.
Sóng dừng tạo trên một sợi dây đàn hồi có chiều dài ℓ với hai đầu tự do. Người ta thấy trên dây có những điểm dao động cách nhau ${{\ell }_{1}}=\dfrac{\ell }{16}$ thì dao động với biên độ a1 người ta lại thấy những điểm cứ cách nhau một khoảng \[{{\ell }_{2}}\] thì các điểm đó có cùng biên độ a2 (a2 > a1) Số điểm bụng trên dây là
[A]. 9
[B]. 8
[C]. 5
[D]. 4
Các điểm cách đều nhau ℓ1 và ℓ2 đều dao động nên các điểm này không phải là các điểm nút a1 < a2
→ ℓ1 = \[\dfrac{\lambda }{4}\] và ℓ2 = \[\dfrac{\lambda }{2}\] → ℓ1 = \[\dfrac{\lambda }{4}\] = \[\dfrac{l}{16}\]
→ ℓ = 4λ. Vì hai đầu dây tự do nên → Số điểm bụng trên dây là: là 4. 2 + 1 = 9
Câu 10.
Một sợi dây đàn hồi OM = 180 cm có hai đầu cố định. Khi được kích thích trên dây hình thành 5 bụng sóng, biên độ dao động của phần tử tại bụng sóng là 3 cm. Tại điểm N gần đầu O nhất, các phần tử có biên độ dao động là $1,5\sqrt{2}$ cm. Khoảng cách ON bằng
[A]. 18 cm.
[B]. 36 cm.
[C]. 9,0 cm.
[D]. 24 cm.
$\ell =5\dfrac{\lambda }{2}\Rightarrow \lambda =72(cm);{{A}_{N}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|\Rightarrow x=9(cm)$
Câu 11.
Một sóng dừng trên dây căng ngang với hai đầu cố định, bụng sóng dao động với biên độ 2a. Ta thấy những điểm không phải nút hoặc bụng, có cùng biên độ ở gần nhau, cách đều nhau 12 cm. Bước sóng và biên độ của những điểm đó
[A]. 24 cm và \[a\sqrt{3}\]
[B]. 24 cm và a
[C]. 48 cm và \[a\sqrt{3}\]
[D]. 48 cm và \[a\sqrt{2}\]
Tương tự câu 8 gọi khoảng cách ngắn nhất giữa chúng là d = 12cm . Biên độ ${{A}_{M}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|=2a\left| \sin \dfrac{2\pi \dfrac{d}{2}}{4d} \right|=a\sqrt{2}$
Câu 12.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách hai nút sóng liên tiếp là 12 cm. C và D là hai phần tử trên dây cùng nằm trên một bó sóng, có cùng biên độ dao động 4 cm và nằm cách nhau 4 cm. Biên độ dao động của điểm bụng là
[A]. 8 cm.
[B]. 4,62 cm.
[C]. 5,66 cm.
[D]. 6,93 cm.
Khoảng cách 2 nút liên tiếp là $\dfrac{\lambda }{2}=12$ Xét gốc tọa độ tại nút gần C nhất ${{x}_{C}}=\dfrac{\dfrac{\lambda }{2}-CD}{2}=\dfrac{12-4}{2}=4(cm)$ Ta có ${{A}_{C}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|=4\Rightarrow {{A}_{b}}=\dfrac{4}{\left| \sin \dfrac{2\pi . 4}{24} \right|}=\dfrac{8\sqrt{3}}{3}\approx 4,62(cm)$
Câu 13.
Sóng dừng tạo trên một sợi dây đàn hồi có chiều dài l. Người ta thấy trên dây có những điểm dao động cách nhau l1 thì dao động với biên độ 4 cm, người ta lại thấy những điểm cứ cách nhau một khoảng l2 (l2 > l1) thì các điểm đó có cùng biên độ a. Giá trị của a là:
[A]. $4\sqrt{2}$cm
[B]. 4 cm
[C]. $2\sqrt{2}$cm
[D]. 2 cm
Khi có sóng dừng, các điểm cách đều nhau dao động với cùng biên độ gồm 3 loại:
* Các bụng sóng B: Khoảng cách giữa 2 điểm liền kề \[\dfrac{\lambda }{2}\]
Biên độ dao động là aB = 2a
* Các điểm nút sóng N: Khoảng cách giữa 2 điểm liền kề \[\dfrac{\lambda }{2}\]
Biên độ dao động là aN = 0
* Các điểm M: Khoảng cách giữa 2 điểm liền kề \[\dfrac{\lambda }{4}\]
Biên độ dao động là aM = a\[\sqrt{2}\]
Theo bài ra ta có: ℓ2 > ℓ1 : a1 = 4cm ; ℓ1 = \[\dfrac{\lambda }{4}\] → a\[\sqrt{2}\] = 4 cm → a = 2\[\sqrt{2}\] cm
Các điểm cách nhau ℓ2 là các bụng sóng nên a2 = 2a = 4\[\sqrt{2}\]cm .
Câu 14.
Sóng dừng trên dây có bước sóng λ. Hai điểm M và N đối xứng nhau qua một nút sóng và cách nhau một khoảng bằng 0,25λ. Kết luận sai là
[A]. Hai điểm luôn cùng tốc độ dao động.
[B]. Hai điểm dao động với cùng biên độ.
[C]. Pha dao động của hai điểm lệch nhau 0,5π.
[D]. Hai điểm dao động ngược pha nhau
2 điểm (trừ nút) đối xứng nhau qua 1 nút luôn ngược pha nhau.
Câu 15.
Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết Phương trình dao động tại đầu A là uA = acos100πt. Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b (b ≠ 0) cách đều nhau và cách nhau khoảng 1 m. Giá trị của b và tốc độ truyền sóng trên sợi dây lần lượt là
[A]. $a\sqrt{2}$; 200 m/s.
[B]. $a\sqrt{3}$; 150 m/s.
[C]. a; 300 m/s.
[D]. $a\sqrt{2}$; 100 m/s.
Các điểm dao động với biên độ b ≠ 0 và b ≠ 2a (tức là không phải là điểm nút và điểm bụng) cách đều nhau thì khoảng cách giữa hai điểm bằng λ/4 = 1m
→ λ = 4m. Do đó v = λf = 4. 50 = 200 (m/s)
Vẽ hình, ta thấy b = \[\dfrac{2a\sqrt{2}}{2}\] = a\[\sqrt{2}\] (Biên độ của bụng sóng là 2a)
Câu 16.
Trên một sợi dây có sóng dừng với biên độ điểm bụng là 5 cm. Giữa hai điểm M và N trên dây có cùng biên độ dao động 2,5 cm, cách nhau 20 cm các điểm luôn dao động với biên độ nhỏ hơn 2,5 cm. Bước sóng trên dây là
[A]. 120 cm
[B]. 80 cm
[C]. 60 cm
[D]. 40 cm
M và N cách đều nút 1 đoạn : d = 10cm, ta có : aM = 2asin(2π\[\dfrac{d}{\lambda }\] ) (2a = 5cm) → sin(2π\[\dfrac{d}{\lambda }\]) = 1/2 → 2π\[\dfrac{d}{\lambda }\] = π/6 → d = λ/12 → λ = 120cm
Câu 17.
Một sợi dây có sóng dừng hai đầu cố định với tần số 5 Hz. Biên độ dao động của điểm bụng là 2 cm. Khoảng cách gần nhất giữa hai điểm trên hai bó sóng cạnh nhau có cùng biên độ 1 cm là 2 cm. Tốc độ truyền sóng là
[A]. 1,2 m/s
[B]. 0,8 m/s
[C]. 0,6 m/s
[D]. 0,40 m/s
Ta có ${{A}_{M}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|={{A}_{b}}\left| \sin \dfrac{2\pi fx}{v} \right|$ (0 <$\dfrac{2\pi x}{\lambda }\le \dfrac{\pi }{2}$
vì x là tọa độ dương của điểm gần nhất thì có 0 < x ≤ $\dfrac{\lambda }{4}$ ) hay \[1=2\left| \sin \dfrac{2\pi . 5. 0,01}{v} \right|\Rightarrow \sin \dfrac{0,1\pi }{v}=\pm \dfrac{1}{2}\]
$\Rightarrow v=0. 6m/s$
Câu 18.
Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết phương trình dao động tại đầu A là uA = 4cos50πt (cm). Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ a (với a ≠ 0) cách đều nhau và cách nhau khoảng 60 cm. Giá trị của a và tốc độ truyền sóng trên sợi dây lần lượt là
[A]. \[2\sqrt{2}\]cm; 60 m/s.
[B]. \[4\sqrt{3}\]cm; 50 m/s.
[C]. \[4\sqrt{2}\] cm; 80 m/s.
[D]. \[4\sqrt{2}\]cm; 60 m/s.
Các điểm dao động với biên độ a cách đều nhau nên $\dfrac{\lambda }{2}=60+60=120$
và $\dfrac{a}{{{A}_{b}}}=\left| \sin \dfrac{\pi }{4} \right|=\dfrac{1}{\sqrt{2}}\Rightarrow a=4\sqrt{2}(cm)$
$v=\dfrac{\lambda }{T}=\dfrac{\lambda \omega }{2\pi }=\dfrac{240. 50\pi }{2\pi }=6000(cm/s)$ hay v = 60m/s
Câu 19.
Các điểm không phải bụng hoặc nút M, N, P là 3 điểm liên tiếp nhau trên một sợi dây mang sóng dừng có cùng biên độ dao động $2\sqrt{3}$cm, dao động tại N ngược với dao động tại M và MN = 2NP. Biên độ dao động tại điểm bụng sóng là
[A]. $2\sqrt{2}$cm.
[B]. $3\sqrt{2}$cm.
[C]. 4 cm.
[D]. $4\sqrt{2}$cm.
3 điểm liên tiếp nhau cùng biên độ dao động nên MN + NP =$\dfrac{\lambda }{2}$
mà MN = 2NP $\Rightarrow MN=\dfrac{\lambda }{3}$
M, N dao động ngược pha nên lần lượt nằm trên 2 bó sóng cạnh nhau và nút gần nhất là trung điểm của chúng.
Xét gốc tọa độ tại nút đó ${{A}_{N}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|\Rightarrow {{A}_{b}}=\dfrac{{{A}_{N}}}{\left| \sin \dfrac{2\pi \dfrac{MN}{2}}{\lambda } \right|}=\dfrac{2}{\sqrt{3}}{{A}_{N}}=4(cm)$
Câu 20.
M, N, P là 3 điểm liên tiếp nhau trên một sợi dây mang sóng dừng có cùng biên độ 4 cm, dao động tại N cùng pha với dao động tại M. Biết MN = 2NP và tần số góc của sóng là 10 rad /s. Tốc độ dao động tại điểm bụng khi sợi dây có dạng một đọan thẳng
[A]. 80 cm /s
[B]. 40 cm/s
[C]. 120 cm /s
[D]. 60 cm/s
$MN+NP=\dfrac{\lambda }{2};MN=2NP\Rightarrow MN=\dfrac{\lambda }{3}$
Vì M, N cùng pha dao động vậy bụng gần nhất là trung điểm của chúng.
Xét gốc tọa độ tại bụng đó ${{A}_{N}}={{A}_{b}}. \left| \cos \dfrac{2\pi x}{\lambda } \right|\Rightarrow {{A}_{b}}=\dfrac{{{A}_{N}}}{\left| \cos \dfrac{\pi }{3} \right|}=8(cm)\Rightarrow \left| {{v}_{\max }} \right|={{A}_{b}}\omega =8. 10=80(cm/s)$
Câu 21.
Thí nghiệm sóng dừng trên một sợi dây có hai đầu cố định và chiều dài 36 cm , người ta thấy có 6 điểm trên dây dao động với biên độ cực đại. Khoảng thời gian ngắn nhất giữa hai lần dây duỗi thẳng là 0,25 s. Khoảng cách từ bụng sóng đến điểm gần nó nhất có biên độ bằng nửa biên độ của bụng sóng là
[A]. 4 cm
[B]. 2 cm
[C]. 3 cm
[D]. 1 cm
\[\ell = \dfrac{{6\lambda }}{2} \Rightarrow \lambda = 12cm;\dfrac{T}{2} = 0,25 \Rightarrow T = 0,5s\]
\[{a_M} = {a_b}cos\dfrac{{2\pi d}}{\lambda } = \dfrac{{{a_b}}}{2} \Rightarrow cos\dfrac{{2\pi d}}{\lambda } = \dfrac{1}{2} \Rightarrow \dfrac{{2\pi d}}{\lambda } = \dfrac{\pi }{3} \Rightarrow d = \dfrac{\lambda }{6} = 2cm\]
Câu 22.
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Khoảng thời gian giữa hai lần liên tiếp sợi dây duỗi thẳng là 0,1 s, tốc độ truyền sóng trên dây là 3 m/s. Khoảng cách giữa hai điểm gần nhau nhất trên sợi dây dao động cùng pha và có biên độ dao động bằng một nửa biên độ của bụng sóng là:
[A]. 20 cm
[B]. 30 cm
[C]. 10 cm
[D]. 8 cm
T = 2. 0,1 = 0,2 s
Bước sóng : λ = v. T = 0,6 m = 60 cm
Các điểm trong cùng một bó sóng dao động cùng pha
Phương trình sóng dừng tại M cách nút N một khoảng d: \[u=2a\cos (\dfrac{2\pi d}{\lambda }+\dfrac{\pi }{2})\cos (\omega t-\dfrac{\pi }{2})\]
AM = 2a cos(\[\dfrac{2\pi d}{\lambda }\]+\[\dfrac{\pi }{2}\]) = a → cos(\[\dfrac{2\pi d}{\lambda }\]+\[\dfrac{\pi }{2}\]) = \[\dfrac{1}{2}\]
→ \[\dfrac{2\pi d}{\lambda }\]+\[\dfrac{\pi }{2}\] = ±\[\dfrac{\pi }{3}\] + kπ → d = (±\[\dfrac{1}{6}\] – \[\dfrac{1}{4}\] +\[\dfrac{k}{2}\])λ
→ d1 = (-\[\dfrac{1}{6}\] – \[\dfrac{1}{4}\] +\[\dfrac{k}{2}\])π → d1min = (-\[\dfrac{1}{6}\] – \[\dfrac{1}{4}\] +\[\dfrac{1}{2}\])λ → d1min = \[\dfrac{\lambda }{12}\]
→ d2 = (\[\dfrac{1}{6}\] – \[\dfrac{1}{4}\] +\[\dfrac{k}{2}\])λ → d2min = (\[\dfrac{1}{6}\] – \[\dfrac{1}{4}\] +\[\dfrac{1}{2}\])λ → d2min = \[\dfrac{5\lambda }{12}\]
MM’ = d2min – d1min = \[\dfrac{5\lambda }{12}\]- \[\dfrac{\lambda }{12}\] = \[\dfrac{\lambda }{3}\] = 20 cm .
Câu 23.
Một sóng dừng trên dây có bước sóng λ và N là một nút sóng. Hai điểm M1, M2 nằm về hai phía của N và có vị trí cân bằng cách N những đoạn lần lượt là $\dfrac{\lambda }{8}$ và $\dfrac{\lambda }{12}$. Ở cùng một thời điểm mà hai phần tử tại đó có li độ khác không thì tỉ số giữa li độ của M1 so với M2 là
[A]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\sqrt{2}$
[B]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\dfrac{1}{\sqrt{3}}$
[C]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{2}$
[D]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\dfrac{1}{\sqrt{3}}$
Biểu thức của sóng dừng tại điểm M cách nút N: NM = d . Chọn gốc tọa độ tại N
d1 = NM1 = – \[\dfrac{\lambda }{8}\] ; d2 = NM2 = \[\dfrac{\lambda }{12}\]
→ uM = 2acos\[\left( \dfrac{2\pi d}{\lambda }+\dfrac{\pi }{2} \right)\]cos(ωt – \[\dfrac{\pi }{2}\])
Biên độ của sóng tại M: aM = 2acos\[\left( \dfrac{2\pi d}{\lambda }+\dfrac{\pi }{2} \right)\]
a1 = 2acos( \[\dfrac{2\pi }{\lambda }\]\[\dfrac{-\lambda }{8}\] + \[\dfrac{\pi }{2}\]) = 2acos(\[\dfrac{-\pi }{4}\]+\[\dfrac{\pi }{2}\]) = 2acos\[\dfrac{\pi }{4}\] = a\[\sqrt{2}\] (cm)
a2 = 2acos( \[\dfrac{2\pi }{\lambda }\]\[\dfrac{\lambda }{12}\] + \[\dfrac{\pi }{2}\]) = 2acos(\[\dfrac{\pi }{6}\]+\[\dfrac{\pi }{2}\]) = 2acos\[\dfrac{2\pi }{3}\] = – a (cm)
Ở cùng một thời điểm mà hai phần tử tại đó có li độ khác không thì tỉ số giữa li độ của M1 so với M2 là \[\dfrac{{{u}_{1}}}{{{u}_{2}}}\]= \[\dfrac{{{a}_{1}}}{{{a}_{2}}}\] = – \[\sqrt{2}\].
Câu 24.
Một sóng dừng trên dây có bước sóng λ và N là một nút sóng. Hai điểm M1, M2 nằm cùng phía so với N và có vị trí cân bằng cách N những đoạn lần lượt là $\dfrac{\lambda }{8}$ và $\dfrac{\lambda }{12}$. Ở cùng một thời điểm mà hai phần tử tại đó có li độ khác không thì tỉ số giữa li độ của M1 so với M2 là
[A]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\sqrt{2}$
[B]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\dfrac{1}{\sqrt{3}}$
[C]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{2}$
[D]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\dfrac{1}{\sqrt{3}}$
2 điểm nằm cùng phía, xét gốc tọa độ ở nút N ta có: $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\dfrac{\sin \dfrac{2\pi {{x}_{1}}}{\lambda }}{\sin \dfrac{2\pi {{x}_{2}}}{\lambda }}=\dfrac{\sin \dfrac{\pi }{4}}{\sin \dfrac{\pi }{6}}=\sqrt{2}$
Câu 25.
Một sóng dừng trên dây có bước sóng λ và N là vị trí cân bằng của một nút sóng. Hai điểm M1, M2 nằm về hai phía của N và có vị trí cân bằng cách N những đoạn lần lượt là $\dfrac{5\lambda }{8}$ và $\dfrac{5\lambda }{12}$. Ở cùng một thời điểm mà hai phần tử tại đó có li độ khác không thì tỉ số giữa li độ của M1 so với M2 là
[A]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\sqrt{2}$
[B]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\dfrac{1}{\sqrt{3}}$
[C]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{2}$
[D]. $\dfrac{{{u}_{1}}}{{{u}_{2}}}=-\dfrac{1}{\sqrt{3}}$
Xét gốc tọa độ ở nút N ta có: $\dfrac{{{u}_{1}}}{{{u}_{2}}}=\dfrac{sin\dfrac{2\pi {{x}_{1}}}{\lambda }}{sin\dfrac{2\pi {{x}_{2}}}{\lambda }}=\dfrac{sin\dfrac{5\pi }{4}}{sin\left( \dfrac{-5\pi }{6} \right)}=\sqrt{2}$ (2 điểm nằm về 2 phía của N nên có tọa độ trái dấu)
Câu 26.
Một sóng dừng trên dây có bước sóng λ và I là một nút sóng. Hai điểm M1, M2 nằm cùng một phía với I và có vị trí cân bằng cách I những đoạn lần lượt là $\dfrac{\lambda }{6}$ và $\dfrac{\lambda }{4}$. Khi dây không duỗi thẳng thì tỉ số giữa vận tốc của M1 so với M2 là
[A]. $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sqrt{6}}{3}$
[B]. $\dfrac{{{v}_{1}}}{{{v}_{2}}}=-\dfrac{\sqrt{6}}{3}$
[C]. $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sqrt{6}}{2}$
[D]. $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sqrt{3}}{2}$
Gốc tọa độ ở nút I ta có: $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sin \dfrac{2\pi {{x}_{1}}}{\lambda }}{\sin \dfrac{2\pi {{x}_{2}}}{\lambda }}=\dfrac{\sin \dfrac{\pi }{3}}{\sin \dfrac{\pi }{2}}=\dfrac{\sqrt{3}}{2}$
Câu 27.
Trên dây AB có sóng dừng với bước sóng λ, biết bụng sóng có biên độ 4 cm tại vị trí M trên dây AB có biên độ $2\sqrt{3}$cm; N là vị trí trên dây AB gần M nhất có biên độ $2\sqrt{2}$cm. Khoảng cách MN bằng
[A]. $\dfrac{\lambda }{12}$
[B]. $\dfrac{\lambda }{6}$
[C]. $\dfrac{5\lambda }{24}$
[D]. $\dfrac{\lambda }{24}$
Bụng gần M, N nhất làm gốc tọa độ khi đó (với 0 < x ≤ $\dfrac{\lambda }{4}$ ): ${{A}_{M}}={{A}_{b}}. \left| \cos \dfrac{2\pi {{x}_{M}}}{\lambda } \right|\Rightarrow 2\sqrt{3}=4\left| \cos \dfrac{2\pi {{x}_{M}}}{\lambda } \right|\Rightarrow {{x}_{M}}=\dfrac{\lambda }{12}$ .
Tương tự ${{x}_{N}}=\dfrac{\lambda }{8}$
Vậy MN = $\dfrac{\lambda }{8}-\dfrac{\lambda }{12}=\dfrac{\lambda }{24}$
Câu 28.
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là một điểm bụng gần A nhất, C là trung điểm của AB, với AB = 10 cm. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C là 0,2 s. Tốc độ truyền sóng trên dây là
[A]. 2 m/s.
[B]. 0,5 m/s.
[C]. 1 m/s.
[D]. 0,25 m/s.
Ta có biên độ sóng dừng tại một điểm M trên dây, cách đầu cố định A đoạn d là: AM = 2a|sin\[\dfrac{2\pi d}{\lambda }\]| với a là biên độ nguồn sóng.
Ta có:
* Biên độ sóng tại điểm B (\[{{d}_{B}}=\dfrac{\lambda }{4}=10\Rightarrow \lambda =40cm\]): AB = 2a
* Biên độ sóng tại điểm C (\[{{d}_{C}}=\dfrac{AB}{2}=\dfrac{\lambda }{8}\]) → AC = 2a|sin\[\dfrac{2\pi \dfrac{\lambda }{8}}{\lambda }\]| \[=2a. \dfrac{\sqrt{2}}{2}={{A}_{B}}\dfrac{\sqrt{2}}{2}\]
* Vì có thể coi điểm B như một chất điểm dao động điều hoà với biên độ AB, thì thời gian ngắn nhất giữa hai lần điểm B có li độ \[{{A}_{B}}\dfrac{\sqrt{2}}{2}\] là \[\Delta t=\dfrac{T}{4}=0,2\Rightarrow T=0,8s\Rightarrow v=\dfrac{\lambda }{T}=0,5m/s\]
Câu 29.
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là một điểm bụng gần A nhất, C nằm giữa A và B, với AB = 30 cm, \[AC=\dfrac{20}{3}\]cm, tốc độ truyền sóng trên dây là 50 cm/s. Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C là
[A]. 0,2 s.
[B]. \[\dfrac{14}{15}\]s.
[C]. \[\dfrac{2}{15}\]s.
[D]. 0,4 s.
$\lambda =4AB=120(cm)\Rightarrow \omega =\dfrac{2\pi v}{\lambda }=\dfrac{2\pi . 50}{120}=\dfrac{5\pi }{6}$
Xét gốc tọa độ tại nút A ta có: $u={{A}_{b}}sin\dfrac{2\pi x}{\lambda }. \cos \left( \varphi \right)$ ($\varphi $ là pha dao động của phần tử tại B)
hay $u={{A}_{C}}={{A}_{B}}\cos \left( \varphi \right)$
mà ${{A}_{C}}={{A}_{B}}. \left| \sin \dfrac{2\pi AC}{\lambda } \right|\Rightarrow {{A}_{C}}={{A}_{B}}. \sin \dfrac{\pi }{9}$ \[\]
Li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C \[\Delta \varphi =2\arccos \left( \dfrac{{{A}_{C}}}{{{A}_{B}}} \right)=2\arccos \left( \sin \dfrac{\pi }{9} \right)=\dfrac{7\pi }{9}\Rightarrow \Delta t=\dfrac{\Delta \varphi }{\omega }=\dfrac{\dfrac{7\pi }{9}}{\dfrac{5\pi }{6}}=\dfrac{14}{15}\left( s \right)\]
Câu 30.
Một sợi dây đàn hồi căng ngang, đầu A cố định. Trên dây đang có sóng dừng ổn định với bước sóng 30 cm. Gọi B là điểm bụng gần A nhất, C là điểm nằm giữa A và B. Biết AC = 2BC. Khoảng thời gian ngắn nhất giữa hai lần liên tiếp mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C là 0,05 s. Tốc độ truyền sóng là
[A]. 100 cm/s
[B]. 60 cm/s
[C]. 120 cm/s
[D]. 80 cm/s
$AB=\dfrac{\lambda }{4}=\dfrac{30}{4}=7. 5(cm)\Rightarrow AC=\dfrac{2}{3}AB=5(cm)$
Chọn gốc tọa độ ở A ta có: $u={{A}_{b}}sin\dfrac{2\pi x}{\lambda }. \cos \left( \varphi \right)$($\varphi $ là pha dao động của phần tử B)
hay $u={{A}_{C}}={{A}_{B}}sin\dfrac{2\pi AB}{\lambda }. \cos \left( \varphi \right)$
mà ${{A}_{C}}={{A}_{B}}. \left| \sin \dfrac{2\pi AC}{\lambda } \right|\Rightarrow \cos (\varphi )=\sin \dfrac{\pi }{3}=\cos \dfrac{\pi }{6}$
Ta có $\omega =\dfrac{2\dfrac{\pi }{6}}{{{t}_{\min }}}=\dfrac{20\pi }{3}hay\dfrac{2\pi v}{\lambda }=\dfrac{20\pi }{3}\Rightarrow v=100(m/s)$
Câu 31.
Trên một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất với AB = 18cm, M là một điểm trên dây cách B một khoảng 12cm. Biết rằng trong một chu kỳ sóng, khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn tốc độ cực đại của phần tử M là 0,1 s. Tốc độ truyền sóng trên dây là
[A]. 4,8 m/s.
[B]. 2,4 m/s.
[C]. 3,2 m/s.
[D]. 5,6 m/s.
A là nút B là bụng khoảng cách AB = λ/4 → λ =72 (cm); MA = AB – MB = 6(cm)
Biên độ dao động tại B là a thì biên độ dao động tại điểm M cách A một khoảng d là ${{a}_{M}}=a\sin \dfrac{2\pi d}{\lambda }=a\sin \dfrac{2\pi . 6}{72}=\dfrac{a}{2}$
Vận tốc cực đại tại M là ${{v}_{M}}=\omega . {{a}_{M}}=\dfrac{1}{2}\omega . a$
Ta xét xem ở vị trí nào thì tốc độ của B bằng vM: $v=\omega . \sqrt{{{a}^{2}}-{{x}^{2}}}=\dfrac{1}{2}\omega . a\Rightarrow \text{ }x=\pm \dfrac{a\sqrt{3}}{2}$
Khi đi từ VTCB ra biên tốc độ giảm, do đó tốc độ của B nhỏ hơn vM trong một phần tư chu kỳ khi vật đi từ $\text{ }x=\dfrac{a\sqrt{3}}{2}$ đến biên a; mà thời gian đó là $\dfrac{T}{12}\Rightarrow \dfrac{T}{12}=\dfrac{0,1}{4}\Leftrightarrow T=0,3(s)$ Vậy $v=\dfrac{\lambda }{T}=\dfrac{72}{0,3}=240\text{ }(cm/s)$ =2,4 (m/s)
Câu 32.
Sóng dừng trên dây nằm ngang. Trong cùng bó sóng, A là nút, B là bụng, C là trung điểm AB. Biết CB = 4 cm. Thời gian ngắn nhất giữa hai lần C và B có cùng li độ là 0,13 s. Tốc độ truyền sóng trên dây là
[A]. 1,23 m/s
[B]. 2,46 m/s
[C]. 3,24 m/s
[D]. 0,98 m/s
C, B có cùng li độ chỉ khi chúng ở VTCB do đó khoảng thời gian ngắn nhất là ${{t}_{\min }}=\dfrac{T}{2}=0. 13(s)\Rightarrow T=0. 26(s)$
Ta có $\lambda =4AB=8CB=8.4=32(cm)\Rightarrow v=\dfrac{\lambda }{T}=\dfrac{32}{0. 26}\approx 123(cm/s)$
Câu 33.
Sóng dừng trên dây hai đầu cố định có bươc sóng là λ, chu kì T. Trong cùng bó sóng, A là nút, B là bụng, C là điểm nằm giữa A,B. Trong một chu kì, khoảng thời gian li độ của B có độ lớn lớn hơn biên độ của C là \[\dfrac{T}{3}\]. Khoảng cách AC là
[A]. \[\dfrac{\lambda }{3}\]
[B]. \[\dfrac{\lambda }{4}\]
[C]. \[\dfrac{\lambda }{6}\]
[D]. \[\dfrac{\lambda }{12}\]
Trong một chu kì, khoảng thời gian li độ của B có độ lớn lớn hơn biên độ của C là \[\dfrac{T}{3}\] suy ra \[\cos \left( \omega \dfrac{T}{3}. \dfrac{1}{4} \right)=\dfrac{{{A}_{C}}}{{{A}_{B}}}=\cos \left( \dfrac{\pi }{6} \right)=\dfrac{\sqrt{3}}{2}(vi\omega =\dfrac{2\pi }{T})\]
Ta xét gốc tọa độ tại nút A: ${{A}_{C}}={{A}_{B}}. \left| \sin \dfrac{2\pi {{x}_{C}}}{\lambda } \right|\Rightarrow \sin \dfrac{2\pi {{x}_{C}}}{\lambda }=\dfrac{\sqrt{3}}{2}\Rightarrow {{x}_{C}}=AC=\dfrac{\lambda }{6}$ (vì x ≤ $\dfrac{\lambda }{4}$ )
Câu 34.
Một sóng dừng trên một sợi dây có dạng u = 40sin(2,5πx)cos(ωt) (mm), trong đó u là li độ tại thời điểm t của một điểm M trên sợi dây mà vị trí cân bằng của nó cách gốc tọa độ O đoạn x(x tính bằng mét, t đo bằng s). Khoảng thời gian ngắn nhất giữa hai lần liên tiếp để một chất điểm trên bụng sóng có độ lớn li độ bằng biên độ của điểm N cách nút sóng 10 cm là 0,125 s. Tốc độ truyền sóng trên sợi dây là:
[A]. 320 cm/s
[B]. 160 cm/s
[C]. 80 cm/s
[D]. 100 cm/s
$\lambda =\dfrac{2\pi }{2. 5\pi }=0. 8(m)$
Ta có ${{A}_{N}}={{A}_{b}}. \left| \sin \dfrac{2\pi x}{\lambda } \right|=40\left| \sin 2,5\pi . 0,1 \right|=20\sqrt{2}{{(mm)}_{{}}}$
$\cos (\omega . \dfrac{0. 125}{2})=\dfrac{{{A}_{N}}}{{{A}_{b}}}=\dfrac{\sqrt{2}}{2}\Rightarrow \omega =4\pi $
mà $v=\dfrac{\lambda \omega }{2\pi }=1. 6(m/s)$
Câu 35.
Phương trình mô tả một sóng dừng có dạng y = 10cos(0,2πx). sin(20πt+$\dfrac{\pi }{4}$), x và y đo bằng cm, t đo bằng giây. Khoảng cách từ một nút sóng, qua 4 bụng sóng đến một nút sóng khác là
[A]. 20 cm.
[B]. 40 cm.
[C]. 10 cm.
[D]. 25 cm.
Từ phương trình sóng dừng: $\dfrac{2\pi }{\lambda }=0. 2\pi \Rightarrow \lambda =10(cm)$
Khoảng cách cần tìm là $4\dfrac{\lambda }{2}=20(cm)$
Câu 36.
Một sợi dây AB dài 20cm, hai đầu cố định. Khi xảy ra hiện tượng sóng dừng các điểm trên dây dao động với phương trình\[u=0,6\sin \left( \dfrac{\pi }{2}x \right)\cos \left( 20\pi t-\dfrac{\pi }{4} \right)\], trong đó x tính bằng cm, t tính bằng giây. Số điểm bụng và điểm nút sóng trên đoạn dây (kể cả A, B) là
[A]. 8 bụng, 8 nút.
[B]. 9 bụng, 10 nút.
[C]. 10 bụng, 11 nút.
[D]. 8 bụng, 9 nút.
Từ PT sóng dừng: $\dfrac{2\pi }{\lambda }=\dfrac{\pi }{2}\Rightarrow \lambda =4(cm)$ $\Rightarrow k=\dfrac{2l}{\lambda }=10$
Vậy có 10 bụng, 11 nút
Câu 37.
Sóng dừng trên một sợi dây có dạng: \[u=a\sin \left( bx \right)\cos \left( \omega t \right)\], trong đó u là li độ dao động của phần tử trên dây mà vị trí cân bằng của nó có tọa độ x, x đo bằng m, t đo bằng giây. Bước sóng là 50 cm. Biên độ của một phần tử cách bụng sóng \[\dfrac{1}{24}\]m là \[\sqrt{3}\]mm. Giá trị a, b lần lượt là
[A]. 2 cm, 4π.
[B]. 2 mm, 4π.
[C]. \[\sqrt{3}\] mm, 2π.
[D]. \[2\sqrt{3}\] mm, 4π
Ta có: $b=\dfrac{2\pi }{\lambda }=\dfrac{2\pi }{0. 5}=4\pi $
Chọn gốc O ở điểm bụng: $A=\sqrt{3}=a\cos (4\pi x)=a\cos (4\pi \dfrac{1}{24})=\dfrac{a\sqrt{3}}{2}\Rightarrow a=2(mm)$
Câu 38.
Một sóng dừng trên một sợi dây được mô tả bởi phương trình \[u=4\cos \left( \dfrac{\pi x}{4}+\dfrac{\pi }{2} \right)c\text{os}\left( 20\pi t-\dfrac{\pi }{2} \right)\]cm, trong đó x đo bằng cm và t đo bằng giây. Tốc độ truyền sóng dọc theo dây là
[A]. 80 cm/s.
[B]. 40 cm/s.
[C]. 60 cm/s.
[D]. 20 cm/s.
PT sóng dừng: \[u=4\cos \left( \dfrac{\pi x}{4}+\dfrac{\pi }{2} \right)c\text{os}\left( 20\pi t-\dfrac{\pi }{2} \right)\]$=4\sin \left( \dfrac{\pi x}{4} \right)c\text{os}\left( 20\pi t+\dfrac{\pi }{2} \right)$ .
Ta thấy: $\dfrac{2\pi }{\lambda }=\dfrac{\pi }{4}\Rightarrow \lambda =8(cm);\omega =20\pi \Rightarrow v=\dfrac{\lambda \omega }{2\pi }=80(cm/s)$
Câu 39.
Một sóng dừng trên một sợi dây có dạng \[u=2\sin \left( \dfrac{\pi }{4}x \right)\cos \left( 10\pi t+\dfrac{\pi }{2} \right)\](cm), trong đó u là li độ tại thời điểm t của một phần tử M trên dây mà vị trí cân bằng của nó cách gốc O một khoảng x (x đo bằng cm, t đo bằng giây). Tốc độ truyền sóng trên dây là
[A]. 80 cm/s.
[B]. 60 cm/s.
[C]. 40 cm/s.
[D]. 20 cm/s.
Từ PT sóng dừng: $\dfrac{2\pi }{\lambda }=\dfrac{\pi }{4}\Rightarrow \lambda =8(cm);\omega =10\pi \Rightarrow v=\dfrac{\lambda \omega }{2\pi }=40(cm/s)$
Câu 40.
Một sợi dây AB dài 24 cm, hai đầu cố định, đang có sóng dừng với hai bụng sóng. Khi dây duỗi thẳng, M và N là hai điểm trên dây chia sợi dây thành ba đoạn bằng nhau. Tỉ số khoảng cách lớn nhất và nhỏ nhất giữa hai điểm M và N trong quá trình sợi dây dao động là 1,25. Biên độ dao động bụng sóng là
[A]. 4 cm.
[B]. 5 cm.
[C]. \[2\sqrt{3}\]cm.
[D]. \[3\sqrt{3}\]cm.
Khoảng cách nhỏ nhất khi MN ở VTCB là $\dfrac{AB}{3}=\dfrac{24}{3}=8(cm)$
Gọi trung điểm MN là O (chính là 1 nút) khi đó OM = 4cm.
Khoảng cách lớn nhất khi MN ở biên là: 8. 1,25 = 10(cm) khi đó OM = 10/2 = 5cm
Vì M, N luôn dao động theo phương vuông góc phương truyền sóng, áp dụng định lý Pitago để tim biên độ dao động của M: ${{A}_{M}}=\sqrt{{{5}^{2}}-{{4}^{2}}}=3(cm)\Rightarrow {{A}_{b}}=\dfrac{{{A}_{M}}}{\left| \sin \dfrac{2\pi {{x}_{M}}}{\lambda } \right|}=\dfrac{3}{\left| \sin \dfrac{2\pi . 4}{24} \right|}=2\sqrt{3}(cm)$
Câu 41.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 24 cm. Biên độ bụng sóng là 3 cm. Gọi N là vị trí của một nút sóng; C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 8 cm và 4 cm. Khoảng cách cực đại giữa C và D trong quá trình dao động là
[A]. 15 cm.
[B]. 12 cm.
[C]. 10 cm.
[D]. 18 cm.
Lấy gốc tọa độ ở nút N ta có: ${{A}_{C}}={{A}_{b}}. \left| \sin \dfrac{2\pi {{x}_{C}}}{\lambda } \right|=3\left| \sin \dfrac{2\pi . 8}{24. 2} \right|=\dfrac{3\sqrt{3}}{2}(cm);$
${{A}_{D}}={{A}_{b}}. \left| \sin \dfrac{2\pi {{x}_{D}}}{\lambda } \right|=3\left| \sin \dfrac{2\pi (-4)}{48} \right|=1. 5(cm)$
suy ra khoảng cách lớn nhất khi C, D đều ở biên theo Pitago: $\sqrt{{{(8+4)}^{2}}+{{(\dfrac{3\sqrt{3}}{2}+1. 5)}^{2}}}\approx 12,68(cm)$
Câu 42.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6 cm. Trên dây có những phần tử sóng dao động với tần số 5 Hz và biên độ lớn nhất là 3 cm. Gọi N là vị trí của một nút sóng; C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5 cm và 7 cm. Tại thời điểm t1, phần tử C có li độ 1,5 cm và đang hướng về vị trí cân bằng. Vào thời điểm t2 = t1 + \[\dfrac{79}{40}\] s, phần tử D có li độ là
[A]. –1,50 cm.
[B]. 1,50 cm.
[C]. – 0,75 cm.
[D]. 0,75 cm.
Ta có: $\dfrac{\lambda }{2}=6\Rightarrow \lambda =12(cm);\omega =2\pi f=10\pi (Hz)$
Xét gốc tọa độ ở nút N:
Tại t1: C có li độ 1. 5 cm đang hướng về VTCB nên: $\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{1. 5}{{{u}_{D1}}}$
Mà $\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{\sin \dfrac{2\pi {{x}_{C}}}{\lambda }}{\sin \dfrac{2\pi {{x}_{D}}}{\lambda }}=\dfrac{\sin \dfrac{2\pi (-10. 5)}{12}}{\sin \dfrac{2\pi *7}{12}}=-\sqrt{2}$
$\Rightarrow {{u}_{D1}}=\dfrac{-3\sqrt{2}}{4}$
Khi đó pha của D: $\cos {{\varphi }_{1}}=\dfrac{{{u}_{D1}}}{{{A}_{D}}}=\dfrac{{{u}_{D1}}}{{{A}_{b}}. \left| \sin \dfrac{2\pi ND}{\lambda } \right|}=\dfrac{{{u}_{D1}}}{\dfrac{3}{2}}=\dfrac{-\sqrt{2}}{2}\Rightarrow {{\varphi }_{1}}=\dfrac{5\pi }{4}$ (vì khi đó D cũng phải hướng về VTCB)
Tại t2: $\dfrac{{{u}_{D1}}}{{{u}_{D2}}}=\dfrac{\cos {{\varphi }_{1}}}{\cos {{\varphi }_{2}}}=\dfrac{\cos {{\varphi }_{1}}}{\cos ({{\varphi }_{1}}+\dfrac{79}{40}\omega )}=\dfrac{\sqrt{2}}{2}\Rightarrow {{u}_{D2}}=-1. 5(cm)$
Câu 43.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6 cm. Trên dây có những phần tử sóng dao động với tần số 5 Hz và biên độ lớn nhất là 3 cm. Gọi N là vị trí của một nút sóng; C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 8 cm và 7,5 cm. Tại thời điểm t1, phần tử C có li độ 2,25 cm và đang hướng ra xa vị trí cân bằng. Vào thời điểm t2 = t1 + \[\dfrac{37}{24}\]s, phần tử D có li độ là
[A]. –1,50 cm.
[B]. 1,50 cm.
[C]. – 0,75 cm.
[D]. 0,75 cm.
Tương tự bài 42: $\lambda =12(cm);\omega =2\pi f=10\pi (Hz)$
Xét gốc tọa độ ở nút N: Tại t1: C có li độ 2. 25 cm đang hướng ra xa VTCB nên:
$\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{2. 25}{{{u}_{D1}}}$
mà $\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{\sin \dfrac{2\pi {{x}_{C}}}{\lambda }}{\sin \dfrac{2\pi {{x}_{D}}}{\lambda }}=\dfrac{\sin \dfrac{2\pi (-8)}{12}}{\sin \dfrac{2\pi *7. 5}{12}}=-\dfrac{\sqrt{6}}{2}$
$\Rightarrow {{u}_{D1}}=\dfrac{-3\sqrt{6}}{4}$
Khi đó pha của D: $\cos {{\varphi }_{1}}=\dfrac{{{u}_{D1}}}{{{A}_{D}}}=\dfrac{{{u}_{D1}}}{{{A}_{b}}. \left| \sin \dfrac{2\pi ND}{\lambda } \right|}=\dfrac{{{u}_{D1}}}{\dfrac{3\sqrt{2}}{2}}=\dfrac{-\sqrt{3}}{2}\Rightarrow {{\varphi }_{1}}=\dfrac{5\pi }{6}$ (vì khi đó D cũng phải hướng ra xa VTCB)
Tại t2: $\dfrac{{{u}_{D1}}}{{{u}_{D2}}}=\dfrac{\cos {{\varphi }_{1}}}{\cos {{\varphi }_{2}}}=\dfrac{\cos {{\varphi }_{1}}}{\cos ({{\varphi }_{1}}+\dfrac{37}{24}\omega )}=\dfrac{-\sqrt{6}}{2}\Rightarrow {{u}_{D2}}=1. 5(cm)$
Câu 44.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6 cm. Trên dây có những phần tử sóng dao động với tần số 5 Hz và biên độ lớn nhất là 3 cm. Gọi N là vị trí của một nút sóng; C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 8 cm và 7,5 cm. Tại thời điểm t1, phần tử C có li độ 2,25 cm và đang hướng ra xa vị trí cân bằng. Vào thời điểm t2 = t1 + \[\dfrac{37}{24}\]s, phần tử D có vận tốc là
[A]. –15π cm/s.
[B]. 15π cm/s.
[C]. – 7,5 cm/s.
[D]. 7,5 cm/s.
$\lambda =12(cm);\omega =2\pi f=10\pi (Hz)$ Xét gốc tọa độ ở nút N: Tại t1: C có li độ 2. 25 cm đang hướng ra xa VTCB nên: $\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{2. 25}{{{u}_{D1}}}$ mà $\dfrac{{{u}_{C1}}}{{{u}_{D1}}}=\dfrac{\sin \dfrac{2\pi {{x}_{C}}}{\lambda }}{\sin \dfrac{2\pi {{x}_{D}}}{\lambda }}=\dfrac{\sin \dfrac{2\pi (-8)}{12}}{\sin \dfrac{2\pi *7. 5}{12}}=-\dfrac{\sqrt{6}}{2}$$\Rightarrow {{u}_{D1}}=\dfrac{-3\sqrt{6}}{4}$ Khi đó pha của D: $\cos {{\varphi }_{1}}=\dfrac{{{u}_{D1}}}{{{A}_{D}}}=\dfrac{{{u}_{D1}}}{{{A}_{b}}. \left| \sin \dfrac{2\pi ND}{\lambda } \right|}=\dfrac{{{u}_{D1}}}{\dfrac{3\sqrt{2}}{2}}=\dfrac{-\sqrt{3}}{2}\Rightarrow {{\varphi }_{1}}=\dfrac{5\pi }{6}$ (vì khi đó D cũng phải hướng ra xa VTCB) Tại t2: ${{v}_{D2}}=-{{A}_{D}}\omega \sin ({{\varphi }_{1}}+\dfrac{37}{24}\omega )=-\dfrac{3\sqrt{2}}{2}. 10\pi \sin (\dfrac{5\pi }{6}+10\pi \dfrac{37}{24})=-15\pi (cm/s)$
Câu 45.
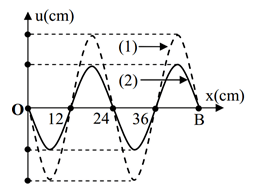
Trên một sợi dây OB căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định. Gọi M, N và P là ba điểm trên dây có vị trí cân bằng cách B lần lượt là 4 cm, 6 cm và 38 cm. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường 1) và t2 = t1 + \[\dfrac{11}{12f}\](đường 2).
Tại thời điểm t1, li độ của phần tử dây ở N bằng biên độ của phần tử dây ở M và tốc độ của phần tử dây ở M là 60 cm/s. Tại thời điểm t2, vận tốc của phần tử dây ở P là
[A]. \[20\sqrt{3}\]cm/s.
[B]. 60 cm/s.
[C]. \[-20\sqrt{3}\]cm/s.
[D]. – 60 cm/s.
Từ đồ thị: $\lambda =\dfrac{\ell }{2}=24(cm);{{x}_{M}}=44;{{x}_{N}}=42;{{x}_{P}}=10$
Suy ra P nằm trên bó sóng đầu tiên và P ngược pha với N,
ta có t1 đến t2 là $\dfrac{T}{2}<\dfrac{11}{12f}=\dfrac{11T}{12}<T$ nên tại t2 thì vP2 < 0
Tại t1: ${{u}_{N1}}={{A}_{M}}={{A}_{N}}\cos (\varphi 1);\left| {{v}_{M1}} \right|=\left| -{{A}_{M}}\omega \sin ({{\varphi }_{1}}) \right|=60$
Ta lại có $\dfrac{{{A}_{M}}}{{{A}_{N}}}=\dfrac{\left| \sin \dfrac{2\pi {{x}_{M}}}{\lambda } \right|}{\left| \sin \dfrac{2\pi {{x}_{N}}}{\lambda } \right|}=\dfrac{\sqrt{3}}{2}\Rightarrow {{\varphi }_{1}}=\dfrac{\pm \pi }{6}\Rightarrow \left| \sin {{\varphi }_{1}} \right|=\dfrac{1}{2}$
$\Rightarrow {{A}_{M}}=\dfrac{120}{\omega }$
$\Rightarrow {{A}_{P}}={{A}_{M}}\dfrac{\left| \sin \dfrac{2\pi {{x}_{P}}}{\lambda } \right|}{\left| \sin \dfrac{2\pi {{x}_{M}}}{\lambda } \right|}=\dfrac{40\sqrt{3}}{\omega }$
Vậy ${{v}_{P2}}=-{{A}_{P}}\omega \sin ((\pi -{{\varphi }_{1}})+\omega \dfrac{11}{12f})=-40\sqrt{3}\sin (\dfrac{8\pi }{3})=-60(cm/s)$ (do ngược pha với N nên ${{\varphi }_{P1}}=\pi -{{\varphi }_{1}}$ )