Bài toán giao thoa sóng cơ xác định vị trí thỏa mãn điều kiện hình học
Câu 1.
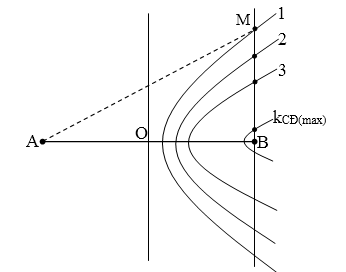
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 25 Hz được đặt tại hai điểm A và B cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Xét các điểm trên mặt nước thuộc đường thẳng vuông góc với AB tại B, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm B một đoạn lớn nhất bằng
[A]. 32,05 cm.
[B]. 30,45 cm.
[C]. 0,41 cm.
[D]. 10,01 cm.
Vẽ hình, thấy rằng điểm M cần tìm thuộc dãy cực đại kCĐ = 1
→ MA – MB = 1.λ mà MA2 – MB2 = AB2
→ 2.MB = $$\dfrac{A{{B}^{2}}}{1.\lambda }-1.\lambda $$ → MB = 30,45 cm
Câu 2.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 25 Hz được đặt tại hai điểm S1 và S2 cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Xét các điểm trên mặt nước thuộc đường thẳng vuông góc với S1S2tại S2, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S2 một đoạn ngắn nhất bằng
[A]. 32,05 cm.
[B]. 30,45 cm.
[C]. 0,41 cm.
[D]. 10,01 cm.
Thấy rằng điểm M cần tìm thuộc dãy cực đại kCĐ(max) = $$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]=6$$
→ MS1 – MS2 = 6.λ mà $$M\text{S}_{1}^{2}-M\text{S}_{2}^{2}={{S}_{1}}S_{2}^{2}$$
→ 2.MS2 = $$\dfrac{{{S}_{1}}S_{2}^{2}}{6.\lambda }-6.\lambda $$ → MS2 = 0,41 cm.
Câu 3.
Tại hai điểm A và B trên mặt chất lỏng có hai nguồn phát sóng cơ cùng pha cách nhau AB = 8 cm, dao động với tần số 20 Hz. Một điểm M trên mặt nước, cách A một khoảng 25 cm và cách B một khoảng 20,5 cm, dao động với biên độ cực đại. Giữa M và đường trung trực của AB có hai vân giao thoa cực đại. Coi biên độ sóng truyền đi không giảm. Điểm Q thuộc đường thẳng vuông góc với AB tại A. Điểm Q dao động với biên độ cực tiểu cách A lớn nhất một đoạn bao nhiêu?.
[A]. 42,3 cm
[B]. 20,6 cm
[C]. 1,4 cm
[D]. 0,5 cm
M dao động với biên độ cực đại, giữa M và trung trực còn 2 dãy cực đại → M thuộc dãy cực đại thứ 3
→ MA – MB = 3λ → λ = 1,5 cm
Vẽ hình và dễ thấy rằng điểm Q cần tìm thuộc dãy cực tiểu kCT = 1
→ QB – QA = 0,5.λ mà QB2 – QA2 = AB2
→ 2.QA = $$\dfrac{A{{B}^{2}}}{0,5.\lambda }-0,5.\lambda $$ → QA = 42,3 cm.
Câu 4.
Biết A và B là 2 nguồn sóng nước giống nhau cách nhau 4 cm. C là một điểm trên mặt nước, sao cho \[CA\bot AB\], C dao động với biên độ cực đại. Khoảng cách CA lớn nhất là 4,2 cm. Bước sóng có giá trị
[A]. 0,8 cm
[B]. 3,2 cm
[C]. 2,4 cm
[D]. 1,6 cm
Vẽ hình và dễ thấy rằng điểm C xa A nhất khi thuộc dãy cực đại số 1 (tính từ đường trung trực)
→ CB – CA = 1.λ mà CB2 – CA2 = AB2
→ 2.CA = $$\dfrac{A{{B}^{2}}}{1.\lambda }-1.\lambda $$ = 8,4 cm → λ = 1,6 cm.
Câu 5.
Biết A và B là 2 nguồn sóng nước giống nhau có tần số 20 Hz, cách nhau 20 cm. Tốc độ truyền sóng trên mặt nước là 60 cm/s. C, D là hai điểm trên mặt nước sao cho chúng dao động với biên độ cực đại và ABCD là hình chữ nhật. Giá trị nhỏ nhất của diện tích hình chữ nhật ABCD là
[A]. 42,22 cm2.
[B]. 2,11 cm2.
[C]. 1303,33 cm2.
[D]. 65,17 cm2.
Vẽ hình và dễ thấy rằng diện tích hình chữ nhật ABCD nhỏ nhất khi C và D cách AB đoạn nhỏ nhất hay chúng thuộc dãy cực đại ngoài cùng kCĐ(max) = $$\left[ \dfrac{AB}{\lambda } \right]=6$$→ CA – CB = 6.λ mà CA2 – CB2 = AB2
→ 2.CB = $$\dfrac{A{{B}^{2}}}{6.\lambda }-6.\lambda $$ = 8,4 cm → CB = $$\dfrac{19}{9}$$cm → SABCD = AB.BC = $$\dfrac{380}{9}$$ cm2.
Câu 6.
Trong hiện tượng giao thoa sóng trên mặt chất lỏng, hai nguồn kết hợp S1, S2 cách nhau 10 cm, daođộng cùng pha theo phương thẳng đứng. Tần số của các nguồn là 50 Hz. Tốc độ truyền sóng trên mặt chất lỏng là 75 cm/s. Gọi C là điểm trên mặt chất lỏng thỏa mãn CS1 = CS2 = 10 cm. Xét các điểm trên đoạn thẳng CS2, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S2 một đoạn nhỏ nhất bằng
[A]. 5,72 mm.
[B]. 7,12 mm.
[C]. 6,79 mm.
[D]. 7,28 mm.
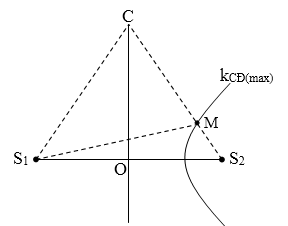
Điểm cần tìm M thuộc dãy cực đại ngoài cùng kCĐ(max)=$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]=6$$
→ MS1 – MS2 = 6.λ = 9 cm (*)
∆CS1S2 đều → $$\widehat{M{{\text{S}}_{2}}{{S}_{1}}}={{60}^{0}}$$
→ \[\cos \widehat{M{{S}_{2}}{{S}_{1}}}=\dfrac{MS_{2}^{2}+{{S}_{1}}S_{2}^{2}-MS_{1}^{2}}{2.M{{S}_{2}}.{{S}_{1}}{{S}_{2}}}\to \dfrac{MS_{2}^{2}+{{10}^{2}}-MS_{1}^{2}}{2.10.M{{S}_{2}}}=\dfrac{1}{2}\] (**)
Từ (*) và (**)→ MS2 ≈ 6,79 cm.
Câu 7.
Biết O và O’ là 2 nguồn sóng nước có cùng biên độ, tần số, nhưng ngược pha nhau và cách nhau 4 cm. Chọn trục tọa độ Ox nằm trên mặt nước và vuông góc với đoạn thẳng OO’, thì điểm không dao động trên trục Ox có tọa độ lớn nhất là 4 cm. Số điểm dao động với biên độ cực đại có trên trục Ox là
[A]. 7
[B]. 6
[C]. 4
[D]. 5
Lưu ý: trong trường hợp 2 nguồn ngược pha thì các dãy cực đại, cực tiểu đảo lộn lại so với cùng pha!
Điểm M không dao động trên Ox có tọa độ lớn nhất (xa O nhất) thuộc dãy cực tiểu số 1
→ MO’ – MO = 1.λ mà MO’2 – MO2 = AB2
→ 2.MO = \[\dfrac{O{{\text{O}}^{/}}^{2}}{1.\lambda }-1.\lambda \] = 8 cm → λ = $$4\sqrt{2}-4$$ (cm)
Số dãy cực đại về một phía đường trung trực là: $$\left[ \dfrac{O{{O}^{/}}}{\lambda }+0,5 \right]$$ = 2, mỗi dãy cực đại này cắt trục Ox tại 2 điểm!
→ có 2 x 2 = 4 điểm dao động với biên độ cực đại trên Ox.
Câu 8.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA = uB = acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 45 cm/s. Gọi MN = 4 cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
[A]. 12,7 cm
[B]. 10,5 cm
[C]. 14,2 cm
[D]. 6,4 cm
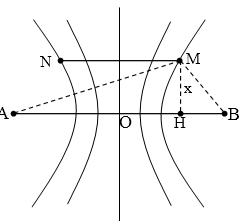
Dễ thấy M và N phải thuộc dãy cực đại số 2 (tính từ đường trung trực)
→ MA – MB = 2.λ (*)→ $$\sqrt{{{x}^{2}}+{{14}^{2}}}-\sqrt{{{x}^{2}}+{{10}^{2}}}=$$ 3 cm
→ x = 10,5 cm.
Hoặc: MA2 – MB2 = AH2 – HB2 = 96
(*)→ MA + MB = 32 cm → MB = 14,5 cm → x = MH = 10,5 cm.
Câu 9.
Tại hai điểm A và B trên mặt nước cách nhau 8 cm có hai nguồn kết hợp dao động với phương trình: \[{{u}_{A}}={{u}_{B}}=a\cos (40\pi t)\], tốc độ truyền sóng trên mặt nước là 30 cm/s. Xét đoạn thẳng CD = 4 cm trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn CD chỉ có 3 điểm dao dộng với biên độ cực đại là
[A]. 3,3 cm.
[B]. 6 cm.
[C]. 8,9 cm.
[D]. 9,7 cm.
Dễ thấy C và D phải thuộc dãy cực đại số 1 (tính từ đường trung trực)
→ DA – DB = 1.λ → \[\sqrt{{{x}^{2}}+{{6}^{2}}}-\sqrt{{{x}^{2}}+{{2}^{2}}}=1,5\] cm.
→ x = 9,7 cm.
Câu 10.
Cho hai nguồn sóng S1 và S2 y hệt nhau cách nhau 8 cm. Về một phía của S1S2 lấy thêm hai điểm S3 và S4 sao cho S3S4 = 4 cm và hợp thành hình thang cân S1S2S3S4. Biết bước sóng bằng 1 cm. Hỏi đường cao của hình thang lớn nhất là bao nhiêu để trên S3S4 có 5 điểm dao động cực đại
[A]. $$2\sqrt{2}$$cm
[B]. $$3\sqrt{5}$$cm
[C]. 4 cm
[D]. $$6\sqrt{2}$$cm
Tương tự câu 8: x = $$3\sqrt{5}$$cm.
Câu 11.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 12 cm, dao động theo phương thẳng đứng với tần số 20 Hz. Tốc độ truyền sóng của mặt chất lỏng là 20 cm/s. Xét đoạn thẳng CD = 4 cm trên mặt nước có chung đường trung trực với AB, C cùng bên với A so với đường trung trực chung đó. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn CD chỉ có 5 điểm dao động với biên độ cực đại là
[A]. $$\sqrt{105}$$ cm.
[B]. $$\sqrt{117}$$ cm.
[C]. $$\sqrt{135}$$ cm.
[D]. $$\sqrt{113}$$ cm.
Tương tự câu 8: x = $$\sqrt{105}$$cm.
Câu 12.
Tại mặt thoáng của một chất lỏng có hai nguồn phát sóng kết hợp A và B cách nhau 8 cm. Cho A, B dao động điều hòa, cùng pha, theo phương vuông góc với mặt chất lỏng. Bước sóng của sóng trên mặt chất lỏng là 1 cm. Gọi M, N là hai điểm thuộc mặt chất lỏng sao cho MN = 4 cm và AMNB là hình thang cân. Để trên đoạn MN có đúng 5 điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang là
[A]. $$\text{18}\sqrt{\text{5}}\text{ c}{{\text{m}}^{\text{2}}}$$.
[B]. $$9\sqrt{3}\text{ c}{{\text{m}}^{\text{2}}}$$.
[C]. $$9\sqrt{\text{5}}\text{ c}{{\text{m}}^{\text{2}}}$$.
[D]. $$\text{18}\sqrt{3}\text{ c}{{\text{m}}^{\text{2}}}$$.
Tương tự câu 8: x = $$3\sqrt{5}$$cm→ \[{{\text{S}}_{AMNB}}=\dfrac{1}{2}(AB+MN).x=18\sqrt{5}\]cm2.
Câu 13.
Xét hiện tượng giao thoa sóng với hai nguồn phát sóng nước cùng pha \[{{S}_{1}},{{S}_{2}}\]với \[{{S}_{1}}{{S}_{2}}=4,2\text{ }cm,\] khoảng cách ngắn nhất giữa hai điểm dao động cực đại trên đoạn \[{{S}_{1}}{{S}_{2}}\]là 0,5 cm. Điểm di động C trên mặt nước sao cho \[C{{S}_{1}}\] luôn vuông góc với \[C{{S}_{2}}. \] Khoảng cách lớn nhất từ \[{{S}_{1}}\] đến C khi C nằm trên một vân giao thoa cực đại là
[A]. 4,225 cm
[B]. 4,135 cm
[C]. 4,195 cm
[D]. 4,435 cm
Bước sóng λ = 1 cm.
→ CS1 – CS2 = 4λ = 4 cm mà $$C\text{S}_{1}^{2}+CS_{2}^{2}={{S}_{1}}S_{2}^{2}$$ = 4,22 → $$C{{S}_{1}}\approx 4,195$$ cm
Câu 14.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 15 Hz được đặt tại hai điểm S1 và S2 cách nhau 10 cm. Xét các điểm trên mặt nước thuộc đường tròn đường kính S1S2, điểm mà phần tử tại đó dao động với biên độ cực tiểu cách đường trung trực của S1S2 một đoạn ngắn nhất là 1,4 cm. Tốc độ truyền sóng trên bề mặt chất lỏng là
[A]. 0,42 m/s.
[B]. 0,6 m/s.
[C]. 0,3 m/s.
[D]. 0,84 m/s.
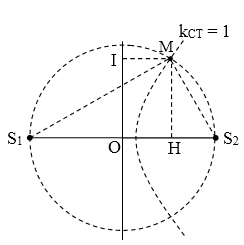
Rõ ràng M thuộc đường cực tiểu số 1 → MS1 – MS2 = 0,5.λ (*)
Bài cho MI = OH = 1,4 cm mà ∆MS1S2 vuông tại M
→ $$M{{\text{S}}_{1}}=\sqrt{{{S}_{1}}H.{{S}_{1}}{{S}_{2}}}=$$ 8cm và $$M{{\text{S}}_{2}}=\sqrt{{{S}_{2}}H.{{S}_{1}}{{S}_{2}}}=$$ 6cm
(*)→ λ = 4 cm → v = 60 cm/s.
Câu 15.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S1 và S2 cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 75 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S1, bán kính S1S2, điểm mà phần tử tại đó dao động với biên độ cực tiểu cách điểm S2 một đoạn ngắn nhất bằng
[A]. 85 mm.
[B]. 2,5 mm.
[C]. 10 mm.
[D]. 89 mm.
Dễ thấy điểm M cần xác định thuộc dãy cực tiểu ngoài cùng kCT(max) =$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda }+0,5 \right]=7$$ về phía S2!
→ MS1 – MS2 = 6,5.λ mà MS1 = S1S2 = 10 cm → MS2 = 0,25 cm = 2,5 mm.
Câu 16.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số được đặt tại hai điểm S1 và S2 cách nhau 10 cm. Xét các điểm trên mặt nước thuộc đường tròn tâm S1, bán kính S1S2, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S2 một đoạn ngắn nhất và xa nhất lần lượt là a và b. Cho biết b – a = 12 cm. Số điểm dao động với biên độ cực tiểu trên đoạn thẳng nối hai nguồn là
[A]. 2.
[B]. 3.
[C]. 4.
[D]. 5.
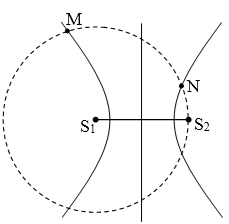
Gọi N và M lần lượt là điểm dao động biên độ cực đại gần và xa S2 nhất, dĩ nhiên 2 điểm này thuộc dãy cực đại ngoài cùng kCĐ(max) =$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$
→ NS1 – NS2 = $$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$.λ hay 10 – a =$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$.λ (*)
và MS2 – NS1 = $$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$.λ hay b – 10 =$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$.λ (**)
Cộng từng vế (*) và (**) → b – a = 2$$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]$$.λ → $$\left[ \dfrac{10}{\lambda } \right]=\dfrac{6}{\lambda }$$ $$\in $$ N*
→ λ = 1 cm hoặc 2 cm hoặc 3 cm hoặc 6 cm!
Thấy chỉ với λ = 6 cm là thoả mãn: $$\left[ \dfrac{10}{6} \right]=\dfrac{6}{6}$$= 1, vậy mỗi bên trung trực chỉ có duy nhất 1 dãy cực đại.
→ Số điểm dao động với biên độ cực tiểu trên đoạn nối hai nguồn là: $$\left[ \dfrac{10}{\lambda }+0,5 \right]x2=4$$.
Câu 17.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S1 và S2 cách nhau 20 cm. Tốc độ truyền sóng trên mặt nước là 1,5 m/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S1, bán kính S1S2, điểm mà phần tử tại đó dao động với biên độ cực đại cách đường trung trực của S1S2 một đoạn ngắn là
[A]. 2,775 cm.
[B]. 1,780 cm.
[C]. 2,572 mm.
[D]. 3,246 cm.
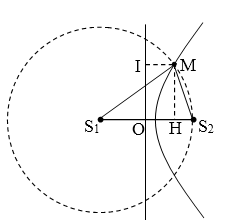
Điểm M cần tìm thuộc dãy cực đại số 1 như hình vẽ
→ MS1 – MS2 =1.λ = 3 cm → MS2 = 17 cm.
Mà: $$\cos \widehat {{S_1}{S_2}M} = {\rm{ }}\dfrac{{{S_1}S_2^2 + MS_2^2 – MS_1^2}}{{2.{S_1}{S_2}.M{S_2}}} = \dfrac{{17}}{{40}} = \dfrac{{H{S_2}}}{{M{S_2}}} \to H{S_2} = 7,225cm$$
→ OH = OS2 – HS2 = 2,775 cm.
Câu 18.
Trên mặt nước có hai nguồn kết hợp A, B dao động cùng pha và cách nhau 8 cm, bước sóng do sóng từ các nguồn phát ra là 3 cm. Điểm M dao động với biên độ cực đại trên đường tròn đường kính AB cách A xa nhất một khoảng là
[A]. 7,9 cm
[B]. 7,8 cm
[C]. 6,7 cm
[D]. 7,6 cm
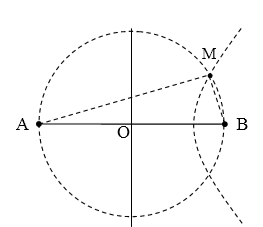
Rõ ràng M thuộc dãy cực tiểu ngoài cùng (phía B) kCĐ(max) = $$\left[ \dfrac{AB}{\lambda } \right]$$= 2
→ MA – MB = 2.λ = 6 cm → MB = MA – 6 (*)
Mà ∆AMB vuông tại M → $$M{{A}^{2}}+M{{B}^{2}}=A{{B}^{2}}={{8}^{2}}$$
Thế (*) → 2MA2 – 12MA – 28 = 0 → MA = 7,8 cm.
Câu 19.
Trong hiện tượng giao thoa sóng hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa cùng pha cùng tần số 40 Hz. Tốc độ truyền sóng trên mặt nước là 1,2 m/s. Xét trên đường tròn tâm A bán kính AB, điểm M nằm trên đường tròn dao động với biên độ cực đại cách đường thẳng AB một đoạn gần nhất và bằng
[A]. 19,675 mm
[B]. 19,975 mm
[C]. 22,973 mm
[D]. 17,964 mm
Tương tự câu 17
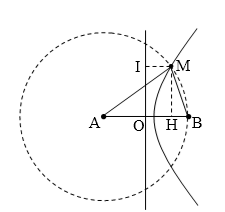
Điểm M cần tìm thuộc dãy cực đại ngoài cùng (phía B) kCĐ(max) = $$\left[ \dfrac{AB}{\lambda } \right]$$= 6
→ MA – MB = 6.λ = 18 cm → MB = 2 cm.
Mà:$$\cos \widehat{ABM}=\dfrac{A{{B}^{2}}+M{{B}^{2}}-M{{A}^{2}}}{2.AB.MB}=\dfrac{1}{20}$$
→ $$\sin \widehat{ABM}=\sqrt{1-\dfrac{1}{{{20}^{2}}}}=\dfrac{MH}{MB}\to MH\approx 19,975$$mm
Câu 20.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S1 và S2 cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 75 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S1, bán kính S1S2, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S2 một đoạn ngắn nhất bằng
[A]. 89 mm.
[B]. 15 mm.
[C]. 85 mm.
[D]. 10 mm.
Điểm M cần tìm thuộc dãy cực đại ngoài cùng (phía S2) kCĐ(max) = $$\left[ \dfrac{{{S}_{1}}{{S}_{2}}}{\lambda } \right]=6$$
→ MS1 – MS2 = 6.λ = 9 cm → MB = 1 cm = 10 mm.
Câu 21.
Trên mặt nước có hai nguồn kết hợp A, B dao động ngược pha và cách nhau 14 cm, bước sóng do sóng từ các nguồn phát ra là 1,8 cm. Điểm M dao động với biên độ cực đại trên đường tròn tâm A bán kính AB và gần trung trực của AB nhất cách trung trực một khoảng bằng
[A]. 0,48 cm
[B]. 0,68 cm
[C]. 0,87 cm
[D]. 0,67 cm
Lưu ý: hai nguồn ngược pha!
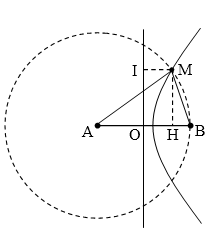
Điểm M cần tìm thuộc dãy cực đại số 1 tính từ đường trung trực đi ra!
→ MA – MB = 0,5.λ = 0,9 cm → MB = 13,1 cm.
Mà:$$\cos \widehat{ABM}=\dfrac{A{{B}^{2}}+M{{B}^{2}}-M{{A}^{2}}}{2.AB.MB}=\dfrac{131}{280}=\dfrac{HB}{MB}\to HB\approx 6,129$$cm
→ OH = OB – HB = 0,871 cm
Câu 22.
Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S1 và S2 cách nhau 16 cm. Tốc độ truyền sóng trên mặt nước là 125 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S1, bán kính 14 cm, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S2 một đoạn ngắn nhất bằng
[A]. 40 mm.
[B]. 80 mm.
[C]. 70 mm.
[D]. 10 mm.
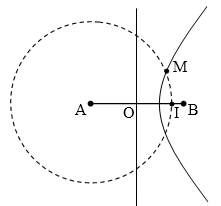
OI = AI – AO = 6 cm.
Điểm M thuộc dãy cực đại gần I nhất tính từ trung trực đi ra kCĐ =$$\left[ \dfrac{OI}{0,5\lambda } \right]=4$$
→ MA – MB = 4.λ = 10 cm → MB = 4 cm.
Câu 23.
Tại mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 10 mm. Điểm C là vị trí cân bằng của phần tử ở mặt nước sao cho AC ⊥ BC. Phần tử nước ở C dao động với biên độ cực đại. Khoảng cách BC lớn nhất bằng
[A]. 37,6 mm.
[B]. 67,6 mm.
[C]. 64,0 mm.
[D]. 68,5 mm.
Câu 24.
Trên mặt nước tại hai điểm S1 và S2 cách nhau 33,8 cm có hai nguồn kết hợp dao động cùng pha, phát ra bước sóng 4 cm. Cho (C) là đường tròn tâm S1bán kính S1S2, Δ là đường thẳng vuông góc với S1S2 đi qua S1. Điểm trên đường tròn (C) dao động với biên độ cực đại cách Δ một đoạn ngắn nhất là
[A]. 1,54 cm.
[B]. 2,13 cm.
[C]. 2,77 cm.
[D]. 2,89 cm.
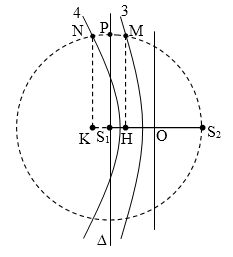
Gọi giao điểm của ∆ và (C) là P có PA = 33,8 cm, PB = $$33,8\sqrt{2}$$cm
→ kP = $$\dfrac{PB-PA}{\lambda }$$ = 3,5
Vậy dãy cực đại thứ 3 và thứ 4 cắt (C) tại những điểm có thể là gần ∆ nhất!
M $$\in $$ dãy cực đại số 3 → MS2 – MS1 = 3λ = 12 cm → MS2 = 45,8 cm.
Xét ∆MS1S2: $$\cos \widehat{M{{S}_{1}}{{S}_{2}}}=\dfrac{MS_{1}^{2}+{{S}_{1}}S_{2}^{2}-MS_{2}^{2}}{2.M{{S}_{1}}.{{S}_{1}}{{S}_{2}}}=0,082=\dfrac{H{{S}_{1}}}{M{{S}_{1}}}\to H{{S}_{1}}=2,77$$cm.
N $$\in $$ dãy cực đại số 4 → NS2 – NS1 = 4λ = 16 cm → MS2 = 49,8 cm.
Xét ∆NS1S2: $$\cos \widehat{N{{S}_{2}}{{S}_{1}}}=\dfrac{NS_{2}^{2}+{{S}_{1}}S_{2}^{2}-NS_{1}^{2}}{2.N{{S}_{2}}.{{S}_{1}}{{S}_{2}}}\approx 0,737=\dfrac{K{{S}_{2}}}{N{{S}_{2}}}\to K{{S}_{2}}=36,687$$cm
→ KS1 = 2,887 cm.
Vậy điểm cần tìm là M cách ∆ đoạn nhỏ nhất 2,77 cm
Câu 25.
Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hoà, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm; NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?
[A]. 1,2 cm.
[B]. 4,2 cm.
[C]. 2,1 cm.
[D]. 3,1 cm.
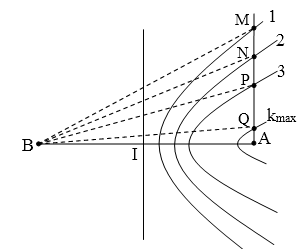
Luôn có: điểm X trên Ax thuộc dãy cực đại thứ k thì $$2.XA=\dfrac{A{{B}^{2}}}{k\lambda }-k\lambda $$ .
Theo bài ra:
\[\left. \begin{array}{l} \bullet M \in k = 1:2MA = \dfrac{{A{B^2}}}{\lambda } – \lambda \\ \bullet N \in k = 2:2NA = \dfrac{{A{B^2}}}{{2\lambda }} – 2\lambda \\ \bullet P \in k = 3:2PA = \dfrac{{A{B^2}}}{{3\lambda }} – 3\lambda \end{array} \right\} \to \left\{ \begin{array}{l}2(MA – NA) = 2MN = 44,5 = \dfrac{{A{B^2}}}{{2\lambda }} + \lambda {\rm{ }}(1)\\2(MA – PA) = 2MP = 62 = \dfrac{{2.A{B^2}}}{{3\lambda }} + 2\lambda {\rm{ }}(2)\end{array} \right.\]
→ Giải (1) và (2), rút ra: AB = 18 cm, λ = 4 cm Q gần A nhất nên thuộc dãy \[{{k}_{\max }}=\left[ \dfrac{AB}{\lambda } \right]=4\to QA=\dfrac{\dfrac{A{{B}^{2}}}{4\lambda }-4\lambda }{2}=2,125\]
Câu 26.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18 cm dao động với uA = uB = acos100πt. Tốc độ truyền sóng của mặt chất lỏng là 125 cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động cùng với hai nguồn. Khoảng cách MO là
[A]. 9 cm.
[B]. $$2\sqrt{10}$$ cm.
[C]. $$\sqrt{19}$$cm.
[D]. 10 cm.
Câu 27.
Trên chất lỏng có hai nguồn sóng A, B cách nhau 13 cm, dao động theo phương thẳng đứng với phương trình là uA = uB = acos50πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 20 cm/s. Khoảng cách ngắn nhất từ nguồn A đến điểm M nằm trên đường trung trực của AB mà phần tử tại M dao động ngược pha với các nguồn là
[A]. 66 mm
[B]. 68 mm.
[C]. 70 mm.
[D]. 72 mm.
Câu 28.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình là uA = uB = acos50πt. Tốc độ truyền sóng của mặt chất lỏng là 50 cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động cùng pha với phần tử chất lỏng tại O. Khoảng cách MO là
[A]. 10 cm.
[B]. $$2\sqrt{10}$$ cm.
[C]. $$2\sqrt{2}$$cm.
[D]. 2 cm.
Câu 29.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 16 cm dao động với uA = uB = acos50πt. Tốc độ truyền sóng ở mặt chất lỏng là 50 cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động ngược pha với phần tử tại O. Khoảng cách MO là
[A]. \[\sqrt{17}\]cm.
[B]. 4 cm.
[C]. \[4\sqrt{2}\] cm.
[D]. \[6\sqrt{2}\]cm
Câu 30.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18 cm dao động với uA = uB = acos50πt. Tốc độ truyền sóng ở mặt chất lỏng là 50 cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động vuông pha với phần tử tại O. Khoảng cách MO là
[A]. \[\sqrt{17}\]cm.
[B]. 3,04 cm.
[C]. \[4\sqrt{2}\] cm.
[D]. \[\sqrt{19}\]cm
Câu 31.
Tại mặt một chất lỏng nằm ngang có hai nguồn sóng O1, O2 cách nhau 24 cm, dao động điều hòa theo phương thẳng đứng với cùng phương trình u = Acoswt. Ở mặt chất lỏng, gọi d là đường vuông góc đi qua trung điểm O của đoạn O1O2, M là điểm thuộc d mà phần tử sóng tại M dao động cùng pha với phần tử sóng tại O, đoạn OM ngắn nhất là 9 cm. Số điểm cực tiểu giao thoa trên đoạn O1O2 là:
[A]. 18
[B]. 16
[C]. 20
[D]. 14
Câu 32.
Tại mặt một chất lỏng nằm ngang có hai nguồn sóng O1, O2 cách nhau 24 cm, dao động điều hòa theo phương thẳng đứng với cùng phương trình u = Acoswt. Ở mặt chất lỏng, gọi d là đường vuông góc đi qua trung điểm O của đoạn O1O2, M là điểm thuộc d mà phần tử sóng tại M dao động ngược với phần tử sóng tại O, đoạn OM ngắn nhất là \[\dfrac{\sqrt{505}}{4}\]cm. Số điểm cực đại giao thoa trên đoạn O1O2 là
[A]. 15
[B]. 17
[C]. 19
[D]. 21
Câu 33.
Trên mặt một chất lỏng có hai nguồn sóng O1, O2 cách nhau 24 cm, dao động cùng pha và d là đường trung trực của O1O2, M là điểm thuộc d mà phần tử sóng tại M dao động cùng pha với phần tử sóng tại O, OM = 15 cm; giữa O và M chỉ có 2 điểm dao động ngược pha với O. Số dãy chứa các điểm dao động cực tiểu trên mặt chất lỏng là?
[A]. 18
[B]. 16
[C]. 20
[D]. 14
Câu 34.
Hai nguồn kết hợp S1 và S2 cách nhau một khoảng là 11 cm đều dao động theo phương trình u = acos(20πt) mm trên mặt nước. Biết tốc độ truyền sóng trên mặt nước là 0,4 m/s. Điểm gần nhất dao động ngược pha với các nguồn nằm trên đường trung trực của S1S2 cách nguồn S1 bao nhiêu?
[A]. 32 cm.
[B]. 18 cm.
[C]. 24 cm.
[D]. 6 cm.
Câu 35.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 40 cm dao động theo phương thẳng đứng với phương trình \[{{u}_{A}}={{u}_{B}}=a\cos \left( 10\pi t \right)cm. \] Tốc độ truyền sóng ở mặt chất lỏng 20 cm/s. Điểm M trên trung trực của AB gần A nhất, dao động ngược pha với A cách AB là
[A]. $$2\sqrt{69}$$ cm.
[B]. 26 cm.
[C]. $$2\sqrt{21}$$ cm.
[D]. 22 cm.
Câu 36.
Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20 cm dao động theo phương trình u = acos(ωt) trên mặt nước, coi biên độ không đổi, bước sóng l = 3 cm. Gọi O là trung điểm của AB. Một điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là
[A]. 12 cm
[B]. 10 cm
[C]. 13,5 cm
[D]. 15 cm
Câu 37.
Trên mặt nước có hai nguồn sóng nước giống nhau A và B dao động cùng pha, cách nhau một khoảng 12 cm. C là một điểm trên mặt nước, cách đều hai nguồn và cách trung điểm O của đoạn AB một khoảng CO = 8 cm. Biết bước sóng là 1,6 cm. Số điểm dao động ngược pha với nguồn có trên đoạn CO là
[A]. 4.
[B]. 5.
[C]. 2.
[D]. 3.
Câu 38.
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với tần số 50 Hz. Tốc độ truyền sóng của mặt chất lỏng là 6 m/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động ngược pha với phần tử chất lỏng tại O. Khoảng cách MO là
[A]. $$5\sqrt{6}$$ cm.
[B]. $$6\sqrt{5}$$ cm.
[C]. $$4\sqrt{5}$$ cm.
[D]. $$4\sqrt{6}$$ cm.
Câu 39.
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn A,B dao động cùng pha với tần số 40 Hz cách nhau 25 cm, tốc độ truyền sóng là 60 cm/s. Một điểm M nằm trên đường trung trực của AB cách trung điểm O của AB 16 cm. Trên đoạn OM số điểm dao động cùng pha với nguồn là
[A]. 4.
[B]. 3.
[C]. 6.
[D]. 5.
Câu 40.
Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12 cm đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng 1,6 cm. C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8 cm. Số điểm dao động cùng pha với nguồn ở trên đoạn CD là
[A]. 3.
[B]. 10.
[C]. 5.
[D]. 6.
Câu 41.
Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau 20 cm, đang dao động vuông góc với mặt nước tạo ra bước sóng 2 cm. Gọi C là điểm trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một đoạn 16 cm. Số điểm trên đoạn CO dao động ngược pha với nguồn là
[A]. 5.
[B]. 6.
[C]. 4.
[D]. 3.
Câu 42.
Tại 2 điểm A và B trên mặt nước cách nhau 16 cm có 2 nguồn kết hợp dao động điều hòa cùng tần số, cùng pha nhau, điểm M nằm trên mặt nước và nằm trên đường trung trực của AB cách trung điểm O của AB một khoảng nhỏ nhất bằng \[4\sqrt{5}\]cm luôn dao động cùng pha với O. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, dao động với biên độ cực tiểu cách A một khoảng nhỏ nhất bằng?
[A]. 9,22 cm
[B]. 2,14 cm
[C]. 8,75 cm
[D]. 8,57 cm
Câu 43.
Trong một thí nghiệm giao thoa sóng nước, hai nguồn S1 và S2 cách nhau 16 cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80 Hz. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Ở mặt nước, gọi d là đường trung trực của đoạn S1S2. Trên d, điểm M ở cách S1 10 cm; điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây?
[A]. 6,8 mm.
[B]. 8,8 mm.
[C]. 9,8 mm.
[D]. 7,8 mm.
Câu 44.
Hai mũi nhọn S1, S2 ban đầu cách nhau 8 cm gắn ở đầu một cần rung có tần số f = 100 Hz, được đặt chạm nhẹ vào mặt nước. Tốc độ truyền sóng trên mặt nước là 0,8 m/s. Điểm M cách đều S1, S2 một đoạn 8 cm. Trên đường trung trực của S1, S2 điểm N dao động cùng pha với M, gần M nhất sẽ cách M một đoạn?
[A]. 9,1 mm.
[B]. 8,9 mm.
[C]. 9,8 mm.
[D]. 9,4 mm.