Bài toán độ lệch pha giữa hai điểm trên phương truyền sóng cơ
Câu 1.
Bước sóng là khoảng cách giữa hai điểm
[A]. trên cùng một phương truyền sóng mà dao động tại hai điểm đó ngược pha.
[B]. gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
[C]. gần nhau nhất mà dao động tại hai điểm đó cùng pha.
[D]. trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
Câu 2.
Phát biểu nào sau đây là đúng khi nói về sóng cơ?
[A]. Bước sóng là khoảng cách giữa hai điểm trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
[B]. Sóng cơ truyền trong chất rắn luôn là sóng dọc.
[C]. Sóng cơ truyền trong chất lỏng luôn là sóng ngang.
[D]. Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
Phát biểu đúng là: “Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha”
Câu 3.
Khi nói về sự truyền sóng cơ trong một môi trường, phát biểu nào sau đây đúng?
[A]. Những phần tử của môi trường cách nhau một số nguyên lần bước sóng thì dao động cùng pha.
[B]. Hai phần tử của môi trường cách nhau một phần tư bước sóng thì dao động lệch pha nhau 900.
[C]. Những phần tử của môi trường trên cùng một hướng truyền sóng và cách nhau một số nguyên lần bước sóng thì dao động cùng pha.
[D]. Hai phần tử của môi trường cách nhau một nửa bước sóng thì dao động ngược pha.
Phát biểu đúng là: “Những phần tử của môi trường trên cùng một hướng truyền sóng và cách nhau một số nguyên lần bước sóng thì dao động cùng pha”
Câu 4.
Một sóng hình sin đang lan truyền trong một môi trường. Các phần tử môi trường ở hai điểm nằm trên cùng một hướng truyền sóng và cách nhau một số nguyên lần bước sóng thì dao động
[A]. Cùng pha
[B]. Lệch pha $\dfrac{\pi }{2}$
[C]. Lệch pha $\dfrac{\pi }{4}$
[D]. Ngược pha
Các phần tử môi trường ở hai điểm nằm trên cùng một hướng truyền sóng và cách nhau một số nguyên lần bước sóng thì dao động cùng pha nhau.
Câu 5.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động cùng pha bằng
[A]. λ/4.
[B]. λ.
[C]. λ/2.
[D]. 2λ.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động cùng pha bằng λ
Câu 6.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động ngược pha bằng
[A]. λ/4.
[B]. λ/2.
[C]. λ.
[D]. 2λ.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động ngược pha bằng λ/2.
Câu 7.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động vuông pha (lệch pha 900) là
[A]. λ/4.
[B]. λ/2.
[C]. λ.
[D]. 2λ.
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động vuông pha (lệch pha 900) là λ/4.
Câu 8.
Một sóng truyền trên mặt nước có bước sóng 2 m. Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền dao động cùng pha nhau là
[A]. 0,5 m
[B]. 1 m
[C]. 2 m
[D]. 1,5 m
Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền dao động cùng pha nhau là λ = 2m.
Câu 9.
Một sóng cơ hình sin truyền trong một môi trường. Xét trên một hướng truyền sóng, khoảng cách giữa hai phần tử môi trường
[A]. dao động ngược pha là một phần tư bước sóng.
[B]. dao động cùng pha là một phần tư bước sóng.
[C]. gần nhau nhất dao động cùng pha là một bước sóng.
[D]. gần nhau nhất dao động ngược pha là một bước sóng.
Khoảng cách giữa hai phần tử môi trường gần nhau nhất dao động cùng pha là một bước sóng.
Câu 10.
Một người quan sát sóng trên mặt hồ thấy khoảng cách giữa hai ngọn sóng liên tiếp bằng 2 m và có 6 ngọn sóng qua trước mặt trọng 8 s. Tốc độ truyền sóng trên mặt nước là:
[A]. 3,2 m/s
[B]. 1,25 m/s
[C]. 2,5 m/s
[D]. 3 m/s
+ Hai ngọn sóng liên tiếp cách nhau λ = 2 m. + 6 ngọn sóng đi qua trước mặt trong 5 chu kì → T = 8: 5 = 1,6 s. → v = λ/T = 1,25 m/s.
Câu 11.
Người quan sát chiếc phao trên mặt biển, thấy nó nhô lên cao 10 lần trong khoảng thời gian 27 s. Tính tần số của sóng biển.
[A]. 2,7 Hz.
[B]. 1/3 Hz.
[C]. 270 Hz.
[D]. 10/27 Hz
+ Phao nhô lên cao 10 lần trong khoảng thời gian 27 s→ T = 27: 9 = 3 s. → f = 1/T = 1/3 Hz
Câu 12.
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ.
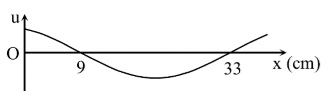
Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng
[A]. 48 cm.
[B]. 18 cm.
[C]. 36 cm.
[D]. 24 cm.
Dễ thấy: $\dfrac{\lambda }{2}=33-9=24cm\to \lambda =48cm.$
Câu 13.
Một người quan sát trên mặt nước biển thấy một cái phao nhô lên 5 lần trong 20 s và khoảng cách giữa hai đỉnh sóng liên tiếp là 2 m. Tốc độ truyền sóng biển là:
[A]. 40 cm/s.
[B]. 50 cm/s.
[C]. 60 cm/s.
[D]. 80 cm/s.
+ Hai ngọn sóng liên tiếp cách nhau λ = 2 m.
+ Khoảng thời gian quan sát phao nhô lên cao 5 lần là 4 chu kì → T = 20: 4 = 5 s.
→ v = λ/T = 40 cm/s.
Câu 14.
Nguồn sóng trên mặt nước tạo dao động với tần số 10 Hz. Biết khoảng cách giữa 7 gợn lồi liên tiếp trên một phương truyền sóng về một phía so với nguồn là 30 cm. Tốc độ truyền sóng trên mặt nước là
[A]. 50 cm/s.
[B]. 150 cm/s.
[C]. 100 cm/s.
[D]. 25 cm/s.
Khoảng cách 7 gợn sóng liên tiếp là 6λ = 30 cm → λ = 5 cm.
→ v = λ. f = 50 cm/s.
Câu 15.
Đặt mũi nhọn S (gắn vào đầu của một thanh thép nằm ngang) chạm mặt nước. Khi lá thép dao động với tần số 120 Hz, tạo trên mặt nước một sóng có biên độ 6 mm, biết rằng khoảng cách giữa 9 gợn lồi liên tiếp trên một phương truyền sóng về một phía so với nguồn (S) là 4 cm. Tốc độ truyền sóng trên mặt nước là
[A]. 120 cm/s
[B]. 40 cm/s
[C]. 100 cm/s
[D]. 60 cm/s
Khoảng cách 9 gợn sóng liên tiếp là 8λ = 4 cm → λ = 0,5 cm.
→ v = λ. f = 60 cm/s.
Câu 16.
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số 120 Hz, tạo ra sóng ổn định trên mặt chất lỏng. Xét 5 gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm 0,5 m. Tốc độ truyền sóng là
[A]. 12 m/s
[B]. 15 m/s
[C]. 30 m/s
[D]. 25 m/s
Gợn thứ nhất cách gợn thứ năm là 4λ = 0,5 m → λ = 0,125 cm. → v = λ. f = 15 m/s.
Câu 17.
Một nguồn âm điểm truyền sóng âm đẳng hướng vào trong không khí với tốc độ truyền âm là v. Khoảng cách giữa 2 điểm gần nhau nhất trên cùng hướng truyền sóng âm dao động ngược pha nhau là d. Tần số của âm là
[A]. $\dfrac{v}{2d}$.
[B]. $\dfrac{2v}{d}$.
[C]. $\dfrac{v}{4d}$.
[D]. $\dfrac{v}{d}$.
$d=\dfrac{\lambda }{2}\text{ hay d = }\dfrac{v}{2f}\to f=\dfrac{v}{2d}$.
Câu 18.
Một sóng cơ có chu kì 2 s truyền với tốc độ 1 m/s. Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền mà tại đó các phần tử môi trường dao động ngược pha nhau là
[A]. 0,5 m.
[B]. 1,0 m.
[C]. 2,0 m.
[D]. 2,5 m.
$d=\dfrac{\lambda }{2}\text{ hay d = }\dfrac{v. T}{2}=\dfrac{1. 2}{2}=1\left( m \right)$.
Câu 19.
Một sóng âm truyền trong thép với tốc độ 5000 m/s. Nếu độ lệch của sóng âm đó ở hai điểm gần nhau nhất cách nhau 1 m trên cùng một phương truyền sóng là 0,5π thì tần số của sóng bằng:
[A]. 1000 Hz
[B]. 1250 Hz
[C]. 5000 Hz
[D]. 2500 Hz.
$d=\dfrac{\lambda }{4}\text{ = 1m}\to \lambda \text{ = 4m }=\text{ }\dfrac{v}{f}\to f=\dfrac{5000}{4}=1250\text{ Hz}$.
Câu 20.
Một cần rung dao động với tần số 20 Hz tạo ra trên mặt nước những gợn lồi và gợn lõm là những đường tròn đồng tâm. Biết tốc độ truyền sóng trên mặt nước là 40 cm/s. Ở cùng một thời điểm, hai gợn lồi liên tiếp (tính từ cần rung) có đường kính chênh lệch nhau
[A]. 4 cm.
[B]. 6 cm.
[C]. 2 cm.
[D]. 8 cm.
Về một phía truyền sóng hai gợn lồi liên tiếp cách nhau $\lambda =\dfrac{v}{f}=2cm$
→ Do đó đường kính chênh lêch nhau 2λ = 4cm.
Câu 21.
Một nguồn phát sóng cơ dao động theo phương trình $u=4\cos \left( 4\pi t-\dfrac{\pi }{4} \right)(cm)$. Biết dao động tại hai điểm gần nhau nhất trên cùng một phương truyền sóng cách nhau 0,5 m có độ lệch pha là $\dfrac{\pi }{3}$. Tốc độ truyền của sóng đó là :
[A]. 1,0 m/s
[B]. 2,0 m/s.
[C]. 1,5 m/s.
[D]. 6,0 m/s.
$\Delta \varphi =\dfrac{2\pi d}{\lambda }=\dfrac{\pi }{3}\to d=\dfrac{\lambda }{6}\text{ = 0}\text{,5 m }\to \lambda =3\text{ }m\to v=\lambda . f=6\text{ m/s}$
Câu 22.
Một sóng âm truyền trong thép với tốc độ 5832 m/s. Nếu độ lệch pha của sóng âm đó ở hai điểm gần nhau nhất cách nhau 1 m trên cùng một phương truyền sóng là $\dfrac{\pi }{4}$thì tần số của sóng bằng
[A]. 729 Hz.
[B]. 970 Hz.
[C]. 5832 Hz.
[D]. 1458 Hz.
$\Delta \varphi =\dfrac{2\pi d}{\lambda }=\dfrac{\pi }{4}\to d=\dfrac{\lambda }{8}\text{ = 1m}\to \lambda =8m=\dfrac{v}{f}\to f=\dfrac{5832}{8}=729\text{ Hz}$
Câu 23.
Sóng cơ có tần số 80 Hz lan truyền trong một môi trường với tốc độ 4 m/s. Dao động của các phần tử vật chất tại hai điểm trên một phương truyền sóng cách nguồn sóng những đoạn lần lượt 31 cm và 33,5 cm, lệch pha nhau góc
[A]. $\dfrac{\pi }{2}$ rad.
[B]. p rad.
[C]. 2p rad.
[D]. $\dfrac{\pi }{3}$ rad.
λ = $\dfrac{v}{f}$ = 5 cm →$\Delta \varphi =\dfrac{2\pi d}{\lambda }=\dfrac{2\pi \left( 33,5-31,5 \right)cm}{5cm}=\pi $.
Câu 24.
Tại điểm S trên mặt nước yên tĩnh có nguồn dao động điều hoà theo phương thẳng đứng với tần số 50 Hz. Khi đó trên mặt nước hình thành hệ sóng tròn đồng tâm S. Tại hai điểm M, N nằm cách nhau 9 cm trên đường thẳng đi qua S luôn dao động cùng pha với nhau. Biết rằng, tốc độ truyền sóng thay đổi trong khoảng từ 70 cm/s đến 80 cm/s. Tốc độ truyền sóng trên mặt nước là
[A]. 75 cm/s.
[B]. 80 cm/s.
[C]. 70 cm/s.
[D]. 72 cm/s.
+ Hai điểm dao động cùng pha: \[d=k\lambda =9cm\text{ hay}\dfrac{\text{kv}}{f}=9\to v=\dfrac{450}{k}\](cm/s)
+ $70\text{cm/s}\le v\le 80\text{cm/s}$ → $70\text{cm/s}\le \dfrac{450}{k}\le 80\text{cm/s}\to 5,6\le \text{k}\le 6,4\Rightarrow k=6\Rightarrow v=75cm\text{/s}$.
Câu 25.
Tại điểm S trên mặt nước yên tĩnh có nguồn dao động điều hoà theo phương thẳng đứng với tần số f. Khi đó trên mặt nước hình thành hệ sóng tròn đồng tâm S. Tại hai điểm M, N nằm cách nhau 5 cm trên đường thẳng đi qua S luôn dao động ngược pha với nhau. Biết tốc độ truyền sóng trên mặt nước là 80 cm/s và tần số của nguồn dao động thay đổi trong khoảng từ 48 Hz đến 64 Hz. Tần số dao động của nguồn là
[A]. 64 Hz.
[B]. 48 Hz.
[C]. 54 Hz.
[D]. 56 Hz.
Hai điểm dao động ngược pha: \[d=\left( k+0,5 \right)\lambda =5cm\text{ hay}\dfrac{\left( \text{k + 0}\text{,5} \right)\text{v}}{f}=5\to f=16\left( k+0,5 \right)\] (Hz)
$48\text{Hz}\le f\le 64\text{Hz}$→ $48\text{Hz}\le 16\left( k+0,5 \right)\le 64\text{Hz}\to 2,5\le \text{k}\le 3,5\Rightarrow k=3\Rightarrow f=56H\text{z}$.
Câu 26.
Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, có tốc độ truyền sóng nằm trong khoảng từ 0,7 m/s đến 1 m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 10 cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau. Tốc độ truyền sóng là
[A]. 100 cm/s
[B]. 80 cm/s
[C]. 85 cm/s
[D]. 90 cm/s
Hai điểm dao động ngược pha: \[d=\left( k+0,5 \right)\lambda =10cm\text{ hay}\dfrac{\left( \text{k + 0}\text{,5} \right)\text{v}}{f}=10\to v=\dfrac{200}{k+0,5}\](cm/s)
$70\text{cm/s}\le v\le 100\text{cm/s}$→ $70\text{cm/s}\le \dfrac{200}{k+0,5}\le 100\text{cm/s}\to 1,5\le \text{k}\le 2,36\Rightarrow k=2\Rightarrow v=80$(cm/s).
Câu 27.
Một sóng ngang truyền trên sợi dây rất dài với tốc độ truyền sóng là 4m/s và tần số sóng có giá trị từ 33 Hz đến 43 Hz. Biết hai phần tử tại hai điểm trên dây cách nhau 25 cm luôn dao động ngược pha nhau. Tần số sóng trên dây là
[A]. 42 Hz.
[B]. 35 Hz.
[C]. 40 Hz.
[D]. 37 Hz.
Hai điểm dao động ngược pha: \[d=\left( k+0,5 \right)\lambda =25cm\text{ hay}\dfrac{\left( \text{k + 0}\text{,5} \right)\text{v}}{f}=25\to f=\dfrac{\left( \text{k + 0}\text{,5} \right)\text{. 400}}{25}=16\left( \text{k + 0}\text{,5} \right)\]
$33H\text{z}\le f\le 43H\text{z}$ → $33H\text{z}\le 16\left( \text{k + 0}\text{,5} \right)\le 43H\text{z}\to 1,56\le \text{k}\le 2,18\Rightarrow k=2\Rightarrow f=40H\text{z}$
Câu 28.
Một dây đàn hồi rất dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là 4 m/s. Xét một điểm M trên dây và cách A một đoạn 40 cm, người ta thấy M luôn luôn dao động lệch pha so với A một góc Dj = (n + 0,5)p với n là số nguyên. Biết tần số f có giá trị trong khoảng từ 8 Hz đến 13 Hz. Tính tần số.
[A]. 10 Hz
[B]. 12,5 Hz
[C]. 8,5 Hz
[D]. 12 Hz
\[\Delta \varphi =\dfrac{2\pi \text{d}}{\pi }=\left( n+0,5 \right)\pi \text{ }(\bot pha)\to d=\left( 2k+1 \right)\dfrac{\lambda }{4}=0,4m\text{ hay}\dfrac{\left( \text{2k + 1} \right)\text{v}}{4f}=0,4\to f=2,5\left( 2k+1 \right)H\text{z}\]
$8\text{Hz}\le f\le 13\text{Hz}$ → $8\text{Hz}\le 2,5\left( 2k+1 \right)\le 13\text{Hz}\to 1,1\le \text{k}\le 2,1\Rightarrow k=2\Rightarrow f=12,5H\text{z}$.
Câu 29.
Một dây đàn hồi rất dài có đầu A dao động với tần số f theo phương vuông góc với sợi dây với tốc độ truyền sóng 20 m/s. Hỏi tần số f phải có giá trị nào để một điểm M trên dây và cách A một đoạn 1 m luôn luôn dao động cùng pha với A. Cho biết tần số 20 Hz ≤ f ≤ 50 Hz
[A]. 10 Hz hoặc 30 Hz
[B]. 20 Hz hoặc 40 Hz
[C]. 25 Hz hoặc 45 Hz
[D]. 30 Hz hoặc 50 Hz
Hai điểm dao động cùng pha: \[d=k\lambda =1m\text{ hay}\dfrac{kv}{f}=1\to f=20k\text{ }\left( H\text{z} \right)\]
$20\text{Hz}\le 20k\le 50\text{Hz}\to 1\le \text{k}\le 2,5\Rightarrow k=1;2\Rightarrow f=20H\text{z or 40Hz}$
Câu 30.
Một sóng cơ lan truyền trong một môi trường với tốc độ 120 cm/s, tần số của sóng thay đổi từ 10 Hz đến 15 Hz. Hai điểm cách nhau 12,5 cm luôn dao động vuông pha. Bước sóng của sóng cơ đó là
[A]. 10,5 cm
[B]. 12 cm
[C]. 10 cm.
[D]. 8 cm
Hai điểm dao động vuông pha: \[d=\left( 2k+1 \right)\dfrac{\lambda }{4}=12,5cm\text{ hay}\dfrac{\left( \text{2k + 1} \right)\text{v}}{4f}=12,5\to f=2,4\left( 2k+1 \right)\text{ }H\text{z}\]
$10\text{Hz}\le f\le 15\text{Hz}$→ $10\text{Hz}\le 2,4\left( 2k+1 \right)\le 15\text{Hz}\to 1,58\le \text{k}\le 2,625\Rightarrow k=2\Rightarrow f=12H\text{z}$ $\Rightarrow \lambda =\dfrac{v}{f}=10\text{ cm}\text{. }$
Câu 31.
Trong hiện tượng truyền sóng cơ với tốc độ truyền sóng là 80 cm/s, tần số dao động có giá trị từ 11 Hz đến 12,5 Hz. Hai điểm trên phương truyền sóng cách nhau 25 cm luôn dao động vuông pha. Bướcsóng là
[A]. 8 cm
[B]. 6,67 cm
[C]. 7,69 cm
[D]. 7,25 cm
Hai điểm dao động vuông pha: \[d=\left( 2k+1 \right)\dfrac{\lambda }{4}=25cm\text{ hay}\dfrac{\left( \text{2k + 1} \right)\text{v}}{4f}=25\to f=\dfrac{\left( \text{2k + 1} \right)\text{. 80}}{4. 25}=0,8. \left( 2k+1 \right)\text{ }H\text{z}\]
$11\text{Hz}\le f\le 12,5\text{Hz}$→ $11\text{Hz}\le 0,8\left( 2k+1 \right)\le 12,5\text{Hz}\to 6,375\le \text{k}\le 7,3125\Rightarrow k=7\Rightarrow f=12H\text{z}$ $\Rightarrow \lambda =\dfrac{v}{f}=6,67\text{cm}\text{. }$
Câu 32.
Trên mặt một chất lỏng, tại O có một nguồn sóng cơ dao động có tần số 30 Hz. Tốc độ truyền sóng v là một giá trị nào đó trong khoảng \[1,6\text{ m/s}<v<2,9\text{ m/s}\]. Biết tại điểm M cách O một khoảng 10 cm sóng tại đó luôn dao động ngược pha với dao động tại O. Giá trị v là
[A]. 2 m/s
[B]. 3 m/s
[C]. 2,4 m/s
[D]. 1,6 m/s
Hai điểm dao động ngược pha: \[d=\left( k+0,5 \right)\lambda =10cm\text{ hay}\dfrac{\left( \text{k + 0}\text{,5} \right)\text{v}}{f}=10\to v=\dfrac{\text{10f}}{\left( \text{k + 0}\text{,5} \right)}=\dfrac{\text{300}}{\left( \text{k + 0}\text{,5} \right)}\left( cm/s \right)\]
\[1,6\text{ m/s}<v<2,9\text{ m/s}\]→ $160\left( cm/s \right)\le \dfrac{\text{300}}{\left( \text{k + 0}\text{,5} \right)}\le 290\left( cm/s \right)\to 0,53\le \text{k}\le 1,375\Rightarrow k=1\Rightarrow v=200\left( cm/s \right)$
Câu 33.
Một nguồn O phát sóng cơ dao động theo phương trình uO = 2cos(20πt + π/3) (trong đó u tính bằng đơn vị mm, t tính bằng đơn vị s). Xét sóng truyền theo một đường thẳng từ O đến điểm M với tốc độ không đổi 1 m/s. Biết M cách O một khoảng 45 cm. Trong khoảng từ O đến M có bao nhiêu điểm dao động cùng pha với dao động tại nguồn O
[A]. 4.
[B]. 3.
[C]. 2.
[D]. 5.
Điểm dao động cùng pha với nguồn thì phải cách nguồn đoạn d = kλ = 10k cm.
Từ O đến M: $0<d\le 45\text{ cm}\to \text{0 10k }\le \text{45 }\to 0<\text{k}\le 4,5\to k=1;\text{ }2;\text{ }3;\text{ }4. $
Câu 34.
Một sóng hình sin truyền theo chiều dương của trục Ox với phương trình dao động của nguồn sóng (đặt tại O) là uO = 4cos100πt (cm). Ở điểm M (theo hướng Ox) cách O một phần tư bước sóng, phần tử môi trường dao động với phương trình là
[A]. uM = 4cos(100πt + π) (cm).
[B]. uM = 4cos100πt (cm).
[C]. uM = 4cos(100πt – 0,5π) (cm).
[D]. uM = 4cos(100πt + 0,5π) (cm).
Sóng từ O đến M nên M chậm pha hơn so với O góc $\dfrac{2\pi \text{d}}{\lambda }=\dfrac{\pi }{2}$ → uM = 4cos(100πt – 0,5π) (cm).
Câu 35.
Một sóng cơ lan truyền trên một đường thẳng từ điểm O đến điểm M cách O một đoạn d. Biết tần số f, bước sóng λ và biên độ a của sóng không đổi trong quá trình sóng truyền. Nếu phương trình dao động của phần tử vật chất tại điểm M có dạng uM(t) = acos2πft thì phương trình dao động của phần tử vật chất tại O là
[A]. \[{{u}_{0}}(t)=a\cos 2\pi (ft-\dfrac{d}{\lambda })\]
[B]. \[{{u}_{0}}(t)=a\cos 2\pi (ft+\dfrac{d}{\lambda })\]
[C]. \[{{u}_{0}}(t)=a\cos \pi (ft-\dfrac{d}{\lambda })\]
[D]. \[{{u}_{0}}(t)=a\cos \pi (ft+\dfrac{d}{\lambda })\]
Sóng từ O đến M nên O nhanh pha hơn so với M góc $\dfrac{2\pi \text{d}}{\lambda }$
→\[{{u}_{0}}(t)=a\cos \left( 2\pi ft+\dfrac{2\pi d}{\lambda } \right)=a\cos 2\pi \left( ft+\dfrac{d}{\lambda } \right)\].
Câu 36.
Sóng cơ truyền từ A đến B trên sợi dây AB rất dài với tốc độ 20 m/s. Tại điểm N trên dây cách A 75 cm, các phần tử ở đó dao động với phương trình uN = 3cos20πt cm, t tính bằng s. Bỏ qua sự giảm biên độ. Phương trình dao động của phần tử tại điểm M trên dây cách A 50 cm là
[A]. uM = 3cos(20πt + π/4) cm.
[B]. uM = 3cos(20πt – π/4) cm.
[C]. uM = 3cos(20πt + π/2) cm.
[D]. uM = 3cos(20πt – π/2) cm.
Rõ ràng M gần nguồn hơn nên nhanh pha hơn N góc
$\dfrac{2\pi \text{d}}{\lambda }=\dfrac{2\pi \left( 75cm-50cm \right)}{200cm}=\dfrac{\pi }{4}$ → uM = 3cos(20πt + $\dfrac{\pi }{4}$).
Câu 37.
Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một nửa bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li độ dao động của phần tử tại M là 3 cm và đang tăng thì li độ dao động của phần tử tại N là
[A]. 6 cm và đang tăng.
[B]. 3 cm và đang giảm.
[C]. – 3 cm và đang giảm.
[D]. 1,5 cm và đang giảm.
M và N cách nhau nửa bước sóng nên dao động ngược pha nhau. Do đó, tại một thời điểm thì trạng thái M và N ngược nhau: $\left\{ \begin{align} & {{u}_{M}}=-{{u}_{N}} \\ & {{v}_{M}}=-{{v}_{N}} \\ \end{align} \right. $
Câu 37.
Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một nửa bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi tốc độ phần tử tại M là 3 cm/s thì tốc độ phần tử tại N là
[A]. 6 cm/s
[B]. – 3 cm/s
[C]. 3 cm/s
[D]. 1,5 cm/s
M và N cách nhau nửa bước sóng nên dao động ngược pha nhau. Do đó, tại một thời điểm thì trạng thái M và N ngược nhau → tốc độ (luôn >0) của M và N tại một thời điểm bằng nhau .
Câu 38.
Một nguồn sóng cơ truyền dọc theo đường thẳng, nguồn dao động với phương trình \[{{u}_{O}}=a\cos (\omega t)\]cm. Một điểm M trên phương truyền sóng cách nguồn một khoảng \[\dfrac{\lambda }{3}\], tại thời điểm 0,5T có li độ uM = 1,5 cm. Coi biên độ sóng không đổi trong quá trình truyền đi, biên độ của sóng là
[A]. 2cm.
[B]. 3 cm.
[C]. 1,5 cm.
[D]. \[2\sqrt{3}\]cm.
Điểm M cách O đoạn \[d=\dfrac{\lambda }{3}\] có phương trình dao động là:
\[{{u}_{M}}=a\cos \left( \omega t-\dfrac{2\pi \text{d}}{\lambda } \right)=a\cos \left( \omega t-\dfrac{2\pi }{3} \right)\]cm
Tại t = 0,5T, pha dao động của M là $\phi =\omega . 0,5T-\dfrac{2\pi }{3}=\dfrac{\pi }{3}$
→ uM = \[\dfrac{a}{2}=\] 1,5 cm → a = 3 cm.
Câu 39.
Cho một sợi dây đàn hồi, thẳng, rất dài. Đầu O của sợi dây dao động với phương trình u = 4cos20πt cm (t tính bằng s). Coi biên độ sóng không đổi khi sóng truyền đi. Tốc độ truyền sóng trên dây là 0,8 m/s. Li độ của điểm M trên dây cách O một đoạn 20 cm theo phương truyền sóng tại thời điểm t = 0,35 s bằng
[A]. $2\sqrt{2}$cm.
[B]. $-2\sqrt{2}$ cm.
[C]. 4 cm.
[D]. – 4 cm.
Bước sóng: \[\lambda =\dfrac{v}{f}=8cm\].
Điểm M cách O đoạn \[d=20cm\] có phương trình dao động là:
\[{{u}_{M}}=4\cos \left( 20\pi t-\dfrac{2\pi \text{d}}{\lambda } \right)=4\cos \left( 20\pi t-5\pi \right)=4\cos \left( 20\pi t-\pi \right)\]cm
Tại t = 0,35s, pha dao động của M là $\phi =20\pi . 0,35-\pi =6\pi \equiv 0\to {{u}_{M}}=4$cm.
Câu 40.
Một sóng cơ lan truyền theo một đường thẳng với biên độ sóng không đổi có phương trình sóng tại nguồn O là uO = acos(ωt – 0,5π) (cm). Một điểm M cách nguồn O bằng $\dfrac{1}{6}$ bước sóng, ở thời điểm $t=\dfrac{0,5\pi }{\omega }$ có li độ $\sqrt{3}$cm. Biên độ sóng a là
[A]. $2\sqrt{3}$cm.
[B]. 2cm.
[C]. $\sqrt{3}$cm.
[D]. 4cm.
Điểm M cách O đoạn \[d=\dfrac{\lambda }{6}\] có phương trình dao động là:
\[{{u}_{M}}=a\cos \left( \omega t-0,5\pi -\dfrac{2\pi \text{d}}{\lambda } \right)=a\cos \left( \omega t-\dfrac{5\pi }{6} \right)\]cm
Tại $t=\dfrac{0,5\pi }{\omega }$, pha dao động của M là \[\phi =\omega . \dfrac{0,5\pi }{\omega }-\dfrac{5\pi }{6}=-\dfrac{\pi }{3}\to {{u}_{M}}=\dfrac{a}{2}(+)=\sqrt{3}\]cm
→ a = $2\sqrt{3}$cm .
Câu 41.
Một sóng cơ học lan truyền theo một đường thẳng có nguồn O dao động \[{{\text{u}}_{\text{o}}}=\text{ acos}\left( \omega t+\dfrac{\pi }{2} \right)\](cm). Ở thời điểm t = \[\dfrac{\pi }{\omega }\], một điểm M cách nguồn bằng một phần ba bước sóng có li độ là uM = -2 cm. Biên độ sóng a là
[A]. 4cm.
[B]. 2 cm.
[C]. \[\dfrac{4}{\sqrt{3}}\]cm.
[D]. \[2\sqrt{3}\] cm
Điểm M cách O đoạn \[d=\dfrac{\lambda }{3}\] có phương trình dao động là:
\[{{\text{u}}_{M}}=\text{ acos}\left( \omega t+\dfrac{\pi }{2}-\dfrac{2\pi \text{d}}{\lambda } \right)=\text{acos}\left( \omega t-\dfrac{\pi }{6} \right)\]cm
Tại $t=\dfrac{\pi }{\omega }$, pha dao động của M là \[\phi =\omega . \dfrac{\pi }{\omega }-\dfrac{\pi }{6}=\dfrac{5\pi }{6}\to {{u}_{M}}=-\dfrac{a\sqrt{3}}{2}(-)=-2\]cm
→ a = $\dfrac{4}{\sqrt{3}}$cm .
Câu 42.
Một sóng cơ học lan truyền trên một phương truyền sóng. Phương trình sóng của một điểm O trên phương truyền sóng đó là : \[{{\text{u}}_{0}}=\text{ acos}(\omega t)\] cm. Ở thời điểm t = \[\dfrac{\pi }{3\omega }\], một điểm M cách O khoảng một phần ba bước sóng có li độ uM = 2 cm. Biên độ sóng a là
[A]. 2 cm.
[B]. 4 cm.
[C]. \[\dfrac{4}{\sqrt{3}}\] cm
[D]. \[2\sqrt{3}\]cm.
Điểm M cách O đoạn \[d=\dfrac{\lambda }{3}\]có phương trình dao động là:
\[{{\text{u}}_{M}}=\text{ acos}\left( \omega t-\dfrac{2\pi \text{d}}{\lambda } \right)=\text{acos}\left( \omega t-\dfrac{2\pi }{3} \right)\]cm
Tại $t=\dfrac{\pi }{3\omega }$, pha dao động của M là \[\phi =\omega . \dfrac{\pi }{3\omega }-\dfrac{2\pi }{3}=-\dfrac{\pi }{3}\to {{u}_{M}}=\dfrac{a}{2}(+)=2\]cm
→ a = 4 cm .
Câu 43.
Tại điểm O trên mặt chất lỏng người ta gây ra dao động với phương trình \[u=2\cos (4\pi t)\,cm\], tốc độ truyền sóng trên mặt chất lỏng là 60 cm/s. Giả sử tại những điểm cách O một đoạn x thì biên độ giảm\[2,5\sqrt{x}\] lần, x tính bằng cm. Dao động tại M cách O một đoạn 25 cm có biểu thức là
[A]. \[u=2\cos \left( 4\pi t-\dfrac{2\pi }{3} \right)cm\].
[B]. \[u=0,16cos\left( 4\pi t+\dfrac{\pi }{3} \right)cm\].
[C]. \[u=0,16\cos \left( 4\pi t-\dfrac{\pi }{3} \right)cm\].
[D]. \[u=2\cos \left( 4\pi t+\dfrac{\pi }{3} \right)cm\]
Bước sóng là: $\lambda =\dfrac{v}{f}=30cm$
Điểm M cách O đoạn x = 25 cm có phương trình dao động là:
\[{{\text{u}}_{M}}=\text{ }\dfrac{\text{a}}{2,5\sqrt{x}}\text{cos}\left( \omega t-\dfrac{2\pi x}{\lambda } \right)=\text{0}\text{,16cos}\left( \omega t-\dfrac{5\pi }{3} \right)\text{=0}\text{,16cos}\left( \omega t+\dfrac{\pi }{3} \right)\]cm.
Câu 44.
Một sóng dọc truyền đi theo phương trục Ox nằm ngang với tốc độ truyền sóng 2 m/s. Phương trình dao động tại O là\[u=\sin \left( 20\pi t-0,5\pi \right)\text{ }mm\]. Thời điểm t = 0,725 s thì một điểm M trên đường Ox, cách O một khoảng 1,3 m có trạng thái chuyển động là
[A]. từ vị trí cực đại đi lên.
[B]. từ vị trí cân bằng đi xuống.
[C]. từ vị trí cân bằng đi lên.
[D]. từ li độ cực đại đi xuống.
Phương trình dao động của O là \[u=\sin \left( 20\pi t-0,5\pi \right)\text{ }mm=\cos \left( 20\pi t-\pi \right)mm\]
Bước sóng là: $\lambda =\dfrac{v}{f}=0,2m$
Điểm M cách O đoạn d = 1,3m có phương trình dao động là:
\[{{\text{u}}_{M}}=\text{ }\cos \left( 20\pi t-\pi -\dfrac{2\pi d}{\lambda } \right)\text{= cos}\left( 20\pi t-14\pi \right)=\cos 20\pi t\]cm.
Tại t = 0,725, pha dao động của M là \[\phi =20\pi . 0,725=14,5\pi \equiv 0,5\pi \to {{u}_{M}}\equiv VTCB(-)\].
Câu 45.
Vào thời điểm t = 0 người ta bắt đầu kích thích để điểm O trên mặt nước dao động theo phương vuông góc với mặt nước, phương trình dao động của sóng tại O là u0 = 2sin(20πt) (mm). Tốc độ truyền sóng trên mặt nước là 4 m/s, coi trong quá trình lan truyền sóng thì biên độ sóng là không đổi. Khi xét sự lan truyền sóng trên mặt nước, nhận xét nào sau đây là đúng
[A]. Hai điểm A, B cách nhau 0,2 m luôn dao động ngược pha.
[B]. Trên đường thẳng từ O, hai điểm M, N cùng phía với O cách nhau 0,05 m dao động vuông pha với nhau.
[C]. Li độ dao động của điểm P cách điểm O một đoạn 0,2 m tại thời điểm t = 0,025 s là uP = -2 mm.
[D]. Sóng trên mặt nước là sóng dọc có bước sóng là 0,4 m.
Bước sóng $\lambda =\dfrac{v}{f}=0,4m$.
+ A và B cách nhau d = 0,2m = $\dfrac{\lambda }{2}$ luôn dao động ngược pha. Đúng!
+ M và N cách nhau d = 0,05m = $\dfrac{\lambda }{8}$ luôn dao động lệch pha nhau
$\Delta \varphi =\dfrac{2\pi \text{d}}{\lambda }=\dfrac{\pi }{4}$ . Sai!
+ Thời gian để sóng truyền từ O đến P là $\Delta t=\dfrac{OP}{v}=0,05\text{s}$
→ tại t = 0,025s thì P chưa nhận nhận sóng truyền tới nên chưa dao động (đứng yên) li độ uP = 0. Sai!
+ Sóng trên mặt nước là sóng ngang chứ không phải sóng dọc. Sai!
Câu 46.
Lúc t = 0 đầu O của dây cao su căng thẳng nằm ngang bắt đầu dao dộng đi lên với biên độ a, chu kì 2 s. Hai điểm gần nhau nhất trên dây dao động cùng pha là 6 cm. Coi biên độ không đổi. Thời điểm đầu tiên để điểm M cách O 6 cm lên đến điểm cao nhất là
[A]. 0,5 s.
[B]. 1 s.
[C]. C.2 s.
[D]. D.2,5 s
Bước sóng λ = 6 cm → tốc độ truyền sóng là: v = $\dfrac{\lambda }{T}=$ 3 cm/s.
Khoảng thời gian để M nhận sóng (bắt đầu đi lên) từ nguồn O là: \[\Delta t=\dfrac{OM}{v}=2s\]
Khoảng thời gian từ lúc điểm M từ lúc nhận sóng (bắt đầu dao động đi lên) đến khi lên vị trí cao nhất (biên dương) là $\dfrac{T}{4}=0,5\text{s}$
→ Thời điểm cần tìm là: $t’=\Delta t+\dfrac{T}{4}=2,5\text{s}$
Câu 47.
Lúc t = 0 đầu O của dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên biên độ a, chu kì 1 s. Hai điểm gần nhau nhất trên dây dao động ngược pha cách nhau 3 cm. Thời điểm đầu tiên để M cách O 12 cm đang đi xuống qua vị trí cân bằng là
[A]. 0,5s.
[B]. 1,5 s.
[C]. 2,5 s.
[D]. 2 s.
Bước sóng λ = 6 cm → tốc độ truyền sóng là: v = $\dfrac{\lambda }{T}=$ 6 cm/s.
Khoảng thời gian để M nhận sóng (bắt đầu đi lên) từ nguồn O là: \[\Delta t=\dfrac{OM}{v}=2s\]
Khoảng thời gian điểm M từ lúc nhận sóng (bắt đầu dao động đi lên) đến khi qua VTCB đi xuống là $\dfrac{T}{2}=0,5\text{s}$
→ Thời điểm cần tìm là: $t’=\Delta t+\dfrac{T}{2}=2,5\text{s}$
Câu 48.
Lúc t = 0 đầu O của dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên biên độ a, chu kì 1 s. Hai điểm gần nhau nhất trên dây dao động cùng pha cách nhau 6 cm. Thời điểm đầu tiên để M cách O 9 cm đến vị trí thấp nhất trong quá trình dao động
[A]. 0,5s.
[B]. 2 s.
[C]. 2,25 s.
[D]. 1,5s.
Bước sóng λ = 6 cm → tốc độ truyền sóng là: v = $\dfrac{\lambda }{T}=$ 6 cm/s.
Khoảng thời gian để M nhận sóng (bắt đầu đi lên) từ nguồn O là: \[\Delta t=\dfrac{OM}{v}=1,5s\]
Khoảng thời gian điểm M từ lúc nhận sóng (bắt đầu dao động đi lên) đến khi tới vị trí thấp nhất là $\dfrac{3T}{4}=0,75\text{s}$
→ Thời điểm cần tìm là: $t’=\Delta t+\dfrac{3T}{4}=2,25\text{s}$
Câu 49.
Sóng truyền từ O đến M phương trình sóng tại O là u = 4sin0,5πt cm. Biết lúc t thì li độ của phần tử M là 2 cm, vậy lúc t + 6 (s) li độ của M là
[A]. -2 cm
[B]. 3 cm
[C]. -3 cm
[D]. 2 cm
M cũng có biên độ và chu kì giống như O: a = 4 cm và T = 4 s
Tại t thì uM = 2 cm, sau đó ∆t = 6s = T + $\dfrac{T}{2}$, trạng thái dao động đảo ngược so với thời điểm t
→ uM = -2 cm.
Câu 50.
Một nguồn O phát sóng cơ dao động theo phương trình\[u=2\cos (20\pi t+\dfrac{\pi }{3})\]( trong đó u tính bằng mm), t tính bằng s) sóng truyền theo đường thẳng Ox với tốc độ không đổi 1 m/s. M là một điểm trên đường truyền cách O một khoảng 42,5 cm. Trong khoảng từ O đến M có bao nhiêu điểm dao động lệch pha π/6 với nguồn
[A]. 9
[B]. 4
[C]. 5
[D]. 8
Bước sóng $\lambda =\dfrac{v}{f}=10cm. $.
Những điểm lệch lệch pha so với O là $\dfrac{\pi }{6}$ hay tổng quát có thể viết
\[\Delta \varphi =\dfrac{2\pi \text{d}}{\lambda }=\left[ \begin{align} & \dfrac{\pi }{6}+2k\pi \text{ }\to d=\dfrac{\lambda }{12}+k\lambda \text{ }\left( 1 \right) \\ & -\dfrac{\pi }{6}+2n\pi \text{ }\to d=-\dfrac{\lambda }{12}+n\lambda \text{ }\left( \text{2} \right) \\ \end{align} \right. \] ;
ở đây d là khoảng cách của điểm lệch pha \[\dfrac{\pi }{6}\] so với O.
Xét các điểm từ O đến M thì: 0 < d ≤ 42,5 cm. (1)
→ \[0<\dfrac{\lambda }{12}+k\lambda \le 42,5\to -\dfrac{1}{12}<k\le 4,167\Rightarrow k=0;\text{ 1; 2; 3; 4}\]→ có 5 điểm! (2)
→ \[0<-\dfrac{\lambda }{12}+k\lambda \le 42,5\to \dfrac{1}{12}<k\le 4,3\Rightarrow k=\text{1; 2; 3; 4}\]→ có 4 điểm!
Vậy có tất cả 9 điểm.
Câu 51.
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng \[\lambda \]. Hai điểm M và N thuộc mặt nước, nằm trên cùng phương truyền sóng cùng phía với O mà các phần tử nước dao động. Biết OM = 4λ; ON = 13λ. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
[A]. 7
[B]. 8
[C]. 10
[D]. 9.

Điểm dao động ngược pha với nguồn O thì phải cách nguồn đoạn d = (k + 0,5)λ
Từ M đến N: $4\lambda \le d\le 13\lambda \to 4\lambda \le \left( k+0,5 \right)\lambda \text{ }\le 13\lambda \text{ }\to 3,5\le \text{k}\le 12,5$
→ có 9 giá trị của k thỏa mãn
Câu 52.
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng \[\lambda \]. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước dao động. Biết OM = 5λ; ON = 13λ và OM vuông góc ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là:
[A]. 7
[B]. 8
[C]. 10
[D]. 9.
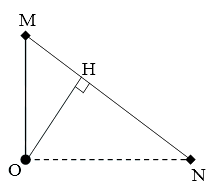
Điểm dao động ngược pha với nguồn O thì phải cách nguồn đoạn d = (k + 0,5)λ = k,5λ
Dễ thấy, H là điểm trên MN cách nguồn O đoạn nhỏ nhất: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{N}^{2}}}\to OH=$ 4,67λ
+ M đến H khoảng cách tới nguồn giảm dần từ 5λ về 4,67λ → không có điểm nào thỏa mãn d = (k + 0,5)λ để ngược pha với nguồn.
+ Từ H đến N khoảng cách tới nguồn tăng dần từ 4,67λ đến 13λ → Có 8 điểm có khoảng cách d = 5,5λ; 6,5λ; 7,5λ; 8,5λ; 9,5λ; 10,5λ; 11,5λ; 12,5λ thỏa mãn ngược pha với nguồn.
→ Vậy có tất cả 8 điểm
Câu 53.
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng \[\lambda \]. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước dao động. Biết OM = 8λ; ON = 12λ và OM vuông góc ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là:
[A]. 5
[B]. 6
[C]. 7
[D]. 4.

Điểm dao động ngược pha với nguồn O thì phải cách nguồn đoạn d = (k + 0,5)λ = k,5λ
Dễ thấy, H là điểm trên MN cách nguồn O đoạn nhỏ nhất: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{N}^{2}}}\to OH=$ 6,66λ
+ Từ M đến H khoảng cách tới nguồn giảm dần từ 8λ về 6,66λ→ Có 1 điểm có khoảng cách d = 7,5λ thỏa mãn ngược pha với nguồn.
+ Từ H đến N khoảng cách tới nguồn tăng dần từ 6,66λ đến 12λ→ Có 5 điểm có khoảng cách d = 7,5λ; 8,5λ; 9,5λ; 10,5λ; 11,5λ thỏa mãn ngược pha với nguồn.
→ Vậy có tất cả 6 điểm.
Câu 54.
Một nguồn sóng O trên mặt chất lỏng dao động với tần số 80 Hz . Cho biết tốc độ truyền sóng trên mặt chất lỏng là 48 cm/s. Trên mặt chất lỏng có hai điểm M,N tạo với O thành một tam giác vuông tại O. Biết OM = 6 cm; ON = 8 cm. Số điểm dao động cùng pha với O trên đoạn MN là
[A]. 9
[B]. 8
[C]. 7
[D]. 6

λ = 0,6 cm → OM = 10λ; ON = $\dfrac{40}{3}\lambda $
Điểm dao động cùng pha với nguồn O thì phải cách nguồn đoạn d = kλ
Dễ thấy, H là điểm trên MN cách nguồn O đoạn nhỏ nhất: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{N}^{2}}}\to OH=$ 8λ
+ Từ M đến H (kể điểm H) khoảng cách tới nguồn giảm dần từ 10λ về 8λ→ Có 3 điểm có khoảng cách d = 10λ; 9λ; 8λ; thỏa mãn ngược pha với nguồn.
+ Từ H(không kể H) đến N khoảng cách tới nguồn tăng dần từ 8λ đến $\dfrac{40}{3}\lambda $→ Có 5 điểm có khoảng cách d = 9λ; 10λ; 11λ; 12λ; 13λ thỏa mãn cùng pha với nguồn.
→ Vậy có tất cả 8 điểm.
Câu 55.
Hai điểm A, B cùng phương truyền sóng cách nhau 21 cm, A và B dao động ngược pha nhau. Trên đoạn AB có 3 điểm dao động cùng pha với A. Tìm bước sóng?
[A]. 6 cm
[B]. 3 cm
[C]. 7 cm
[D]. 9 cm
Gọi M là điểm dao động cùng pha với A trên đoạn AB gần B nhất → AM = 3λ và MB = 0,5λ → AB = 3,5λ → λ = AB: 3,5 = 6 cm.
Câu 56.
Hai điểm A, B cùng phương truyền sóng, cách nhau 24 cm. Trên đoạn AB có 3 điểm A1, A2, A3 dao động cùng pha với A; 3 điểm B1, B2, B3 dao động cùng pha với B. Sóng truyền theo thứ tự A, B1, A1, B2, A2, B3, A3, B, biết AB1 = 3 cm. Bước sóng là
[A]. 6 cm
[B]. 3 cm
[C]. 7 cm
[D]. 9 cm
Có AA3 = BB1 = 3λ → AB = AB1 + B1B → 24 = 3 + 3λ → λ = 7 cm