Một vật dao động điều hòa với chu kì T trên trục Ox. Biết trong một chu kì, khoảng thời gian vật nhỏ có li độ x thoả mãn $\left| x \right|\ge 3$ cm là $\dfrac{T}{2}$. Biên độ dao động của vật là:
[A]. $3\sqrt 2 $ cm
[B]. 4 cm.
[C]. 6 cm.
[D]. 12 cm.
Diễn biến dao động trong một chu kì của vật là
Thời gian thỏa mãn $\left| x \right| \ge 3 \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le – 3\end{array} \right.$ (4 đoạn nhỏ nét liền) là $\dfrac{T}{2}$ → Thời gian dao động trên mỗi đoạn nhỏ là $\dfrac{T}{8}$. Theo trục phân bố thời gian thì $3cm=\dfrac{A\sqrt{2}}{2}\to A=3\sqrt{2}cm$.
Câu 2.
Một vật dao động điều hòa với chu kì T trên trục Ox. Biết trong một chu kì, khoảng thời gian vật nhỏ có li độ x thoả mãn $x\ge 3$ cm là $\dfrac{T}{3}$. Biên độ dao động của vật là:
[A]. $3\sqrt{2}$ cm.
[B]. $3\sqrt{3}$cm.
[C]. 6 cm .
[D]. 12 cm.
Diễn biến dao động trong một chu kì của vật là

Tổng thời gian thỏa mãn $x\ge 3$(2 đoạn nhỏ nét liền) là $\dfrac{T}{3}$ → Thời gian dao động trên mỗi đoạn nhỏ là $\dfrac{T}{6}$.
Theo trục phân bố thời gian thì $3cm=\dfrac{A}{2}\to A=6cm$.
Câu 3.
Một vật dao động điều hòa với chu kì T trên trục Ox. Biết trong một chu kì, khoảng thời gian vật nhỏ có li độ x thoả mãn $x\ge -3$ cm là $\dfrac{5T}{6}$. Biên độ dao động của vật là:
[A]. $3\sqrt{2}$ cm.
[B]. $2\sqrt{3}$cm.
[C]. 6 cm
[D]. 12 cm.
Diễn biến dao động trong một chu kì của vật là

Tổng thời gian thỏa mãn $x\ge -3$ là $\dfrac{5T}{6}$ → Thời gian dao động trên mỗi đoạn nhỏ là $\dfrac{T}{6}$.
Theo trục phân bố thời gian thì $-3cm=-\dfrac{A\sqrt{3}}{2}\to A=2\sqrt{3}cm$.
Câu 4.
Một vật dao động điều hòa với chu kì T. Biết trong một chu kì, khoảng thời gian vật nhỏ con lắc cách vị trí cân bằng không vượt quá 5 cm là $\dfrac{T}{3}$. Biên độ dao động của vật là:
[A]. 5 cm.
[B]. 20 cm.
[C]. 10 cm
[D]. 15 cm.
Câu 5.
Một vật dao động điều hòa với biên độ 6 cm và chu kì 3 s. Trong một chu kì, khoảng thời gian vật nhỏ con lắc dao động cách VTCB một đoạn d thỏa mãn: $3\text{ cm}\le d\le 3\sqrt{3}\text{ cm}$ là
[A]. 2 s.
[B]. 1 s.
[C]. 0,33 s .
[D]. 0,5 s.
Diễn biến dao động trong một chu kì của vật như sau

Thời gian thỏa mãn $3\text{ cm}\le d\le 3\sqrt{3}\text{ cm}$(4 đoạn nét liền) là $\dfrac{T}{3}=1\text{s}$.
Câu 6.
Một vật dao động điều hòa tự do theo phương ngang. Chu kì dao động của con lắc là π (s) Trong một chu kì, thời gian để tốc độ của vật không vượt quá một nửa tốc độ cực đại là
[A]. $\dfrac{\pi }{6}$s
[B]. $\dfrac{2\pi }{3}$s
[C]. $\dfrac{\pi }{3}$s
[D]. $\dfrac{\pi }{4}$s
Diễn biến dao động của vận tốc trong một chu kì của vật như sau:
Thời gian thỏa mãn $\left| v \right|\le \dfrac{{{v}_{\max }}}{2}$ là $\dfrac{T}{3}=\dfrac{\pi }{3}$

Câu 7.
Một vật dao động điều hòa tự do theo phương ngang. Chu kỳ dao động của con lắc là π (s) Trong một chu kì, thời gian vận tốc của vật có giá trị không vượt quá một nửa tốc độ cực đại là
[A]. $\dfrac{\pi }{6}$s
[B]. $\dfrac{2\pi }{3}$s
[C]. $\dfrac{\pi }{3}$s
[D]. $\dfrac{\pi }{4}$s
Diễn biến dao động của vận tốc trong một chu kì của vật như sau:
Thời gian thỏa mãn $v\le \dfrac{{{v}_{\max }}}{2}$ là $\dfrac{2T}{3}=\dfrac{2\pi }{3}$

Câu 8.
Một dao động điều hòa với chu kì T và biên độ 10 cm. Biết trong một chu kì khoảng thời gian vận tốc của vật nhỏ có độ lớn không vượt quá 10π cm/s là $\dfrac{T}{3}$. Tốc độ cực đại có giá trị bằng bao nhiêu?
[A]. $20\sqrt{3}\pi $ cm/s
[B]. $20\sqrt{2}\pi $ cm/s
[C]. $20\pi $cm/s
[D]. $10\sqrt{3}\pi $ cm/s.
Bài toán ngược của Câu 6.
Câu 9.
Con lắc lò xo dao động điều hòa chu kỳ T, chiều dài quỹ đạo 8 cm. Trong một chu kì, thời gian vận tốc của vật có giá trị không nhỏ hơn 8π cm/s là $\dfrac{T}{3}$. Chu kì của vật dao động là?
[A]. 1 s.
[B]. 0,5 s
[C]. 0,25 s.
[D]. 2 s.
Diễn biến dao động của vận tốc trong một chu kì của vật như sau:
Theo trục phân bố thời gian, dễ thấy $8\pi =\dfrac{{{v}_{\max }}}{2}\to {{v}_{\max }}=16\pi \to \omega =4\pi \to T=0,5s$.

Câu 10.
Một vật dao động điều hòa với biên độ 4 cm. Biết rằng trong một chu kỳ dao động, khoảng thời mà tốc độ của vật không lớn hơn $16\pi \sqrt{3}$cm/s là $\dfrac{T}{3}.$ Chu kì dao động của vật là?
[A]. $\dfrac{1}{2\sqrt{3}}s$
[B]. $\dfrac{\sqrt{3}}{2}s$
[C]. $\dfrac{4}{\sqrt{3}}s$
[D]. $\dfrac{1}{4\sqrt{3}}s$
Diễn biến dao động của vận tốc trong một chu kì của vật như sau:

Các đoạn nét liền thời gian dao động mất $\dfrac{T}{3}$ , do đó theo trục phân bố thời gian:
$16\pi \sqrt{3}=\dfrac{{{v}_{\max }}}{2}\to {{v}_{\max }}=32\pi \sqrt{3}$cm/s → ω = $8\pi \sqrt{3}$ → $T=\dfrac{1}{4\sqrt{3}}$ s.
Câu 11.
Một dao động điều hòa với chu kì T và biên độ 10 cm. Biết trong một chu kì khoảng thời gian vận tốc của vật có độ lớn không vượt quá 10π cm/s là $\dfrac{2T}{3}.$ Chu kì dao động của vật là?
[A]. $\sqrt{3}$s
[B]. $\sqrt{2}$s
[C]. 1 s
[D]. 2 s
Diễn biến dao động của vận tốc trong một chu kì của vật như sau:

Các đoạn nét liền thời gian dao động mất $\dfrac{2T}{3}$ , do đó theo trục phân bố thời gian:
$10\pi =\dfrac{{{v}_{\max }}\sqrt{3}}{2}\to {{v}_{\max }}=\dfrac{20\pi \sqrt{3}}{3}$cm/s → ω = $\dfrac{2\pi \sqrt{3}}{3}$ → $T=\sqrt{3}$ s.
Câu 12.
Một chất điểm dao động điều hòa với chu kì T. Gọi vTB là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà $v\ge \dfrac{\pi }{4}{{v}_{TB}}$ là
[A]. $\dfrac{T}{6}$
[B]. $\dfrac{2T}{3}$
[C]. $\dfrac{T}{3}$
[D]. $\dfrac{T}{2}$
Câu 13.
Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s2 là $\dfrac{T}{3}$. Lấy π2=10. Tần số dao động của vật là:
[A]. 4 Hz.
[B]. 3 Hz
[C]. 2 Hz.
[D]. 1 Hz.
Câu 14.
Một vật dao động điều hòa với chu kì T. Biết trong một chu kì, khoảng thời gian để vật có tốc độ không vượt quá 15,7 cm/s là $\dfrac{T}{3}$. Lấy π = 3,14. Tốc độ trung bình vật dao động trong một chu kì là
[A]. 20 cm/s.
[B]. 31,4 cm/s.
[C]. 40 cm/s
[D]. 15,7 cm/s.
Tương tự câu 10, dễ thấy: $15,7=\dfrac{{{v}_{\max }}}{2}\to {{v}_{\max }}=31,4$cm/s → ${{v}_{tb(T)}}=\dfrac{2{{v}_{\max }}}{\pi }=20$cm/s.
Câu 15.
Một chất điểm dao động điều hòa với chu kì T. Gọi vtb là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà $v\le \dfrac{\pi \sqrt{3}}{4}{{v}_{tb}}$ là
[A]. $\dfrac{T}{6}$
[B]. $\dfrac{2T}{3}$
[C]. $\dfrac{T}{3}$
[D]. $\dfrac{T}{2}$
tốc độ $v\le \dfrac{\pi \sqrt{3}}{4}{{v}_{tb}}\Leftrightarrow v\le \dfrac{{{v}_{\max }}\sqrt{3}}{2}$
→ Thời gian thỏa mãn trong một chu kì là $\dfrac{2T}{3}$.
Câu 16.
Một vật dao động điều hòa với chu kì T và biên độ 4 cm. Biết rằng trong một chu kỳ dao động, khoảng thời gian độ lớn gia tốc không vượt quá $50\sqrt{2}$ cm/s2 là $\dfrac{T}{2}.$ Tần số góc dao động của vật bằng
[A]. 2π rad/s
[B]. 5π rad/s
[C]. 5 rad/s
[D]. $5\sqrt{2}$rad/s
Diễn biến dao động của gia tốc trong một chu kì của vật như sau:

Các đoạn nét liền thời gian dao động mất $\dfrac{T}{2}$, do đó theo trục phân bố thời gian:
$50\sqrt{2}=\dfrac{{{a}_{\max }}\sqrt{2}}{2}\to {{a}_{\max }}=100$cm/s2 → ω = 5 rad/s.
Câu 17.
Một chất điểm dao động điều hòa với chu kì T. Gọi vTB là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà v thoả mãn $\dfrac{\pi }{2\sqrt{2}}{{v}_{TB}}\ge v\ge \dfrac{\pi }{4}{{v}_{TB}}$ là
[A]. $\dfrac{T}{6}$
[B]. $\dfrac{2T}{3}$
[C]. $\dfrac{T}{3}$
[D]. $\dfrac{T}{2}$
Diễn biến dao động của vận tốc trong một chu kì của vật như sau

Thời gian thỏa mãn $\dfrac{\pi }{2\sqrt{2}}{{v}_{TB}}\ge v\ge \dfrac{\pi }{4}{{v}_{TB}}\Leftrightarrow \dfrac{{{v}_{\max }}}{2}\le v\le \dfrac{{{v}_{\max }}\sqrt{2}}{2}$ (4 đoạn nét liền) là $4.\dfrac{T}{24}=\dfrac{T}{6}$.
Câu 18.
Một vật khối lượng 100 g dao động điều hòa với chu kì T và biên độ 4 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn lực kéo về không nhỏ hơn 2 N là $\dfrac{2T}{3}$. Lấy π2=10. Chu kì dao động của vật là:
[A]. 0,3 s
[B]. 0,2 s
[C]. 0,4 s.
[D]. 0,1 s.
Diễn biến dao động của lực kéo về trong một chu kì của vật là

Thời gian thỏa mãn (4 đoạn nhỏ nét liền) là $\dfrac{2T}{3}$ → Thời gian dao động trên mỗi đoạn nhỏ là $\dfrac{T}{6}$.
Theo trục phân bố thời gian thì $2N=\dfrac{{{F}_{\max }}}{2}\to {{F}_{\max }}=4N=m{{\omega }^{2}}A\to \omega =10\pi \to T=0,2$s.
Câu 19.
Một con lắc lò xo gồm vật nhỏ khối lượng 200g dao động điều hòa với chu kì T và biên độ 4 cm. Biết rằng trong một chu kì dao động, khoảng thời gian độ lớn gia tốc không nhỏ hơn $500\sqrt{2}$ cm/s2 là $\dfrac{T}{2}.$ Độ cứng con lắc lò xo là
[A]. 20 N/m
[B]. 50 N/m
[C]. 40 N/m
[D]. 30 N/m
Diễn biến dao động của gia tốc trong một chu kì của vật như sau:

Các đoạn nét liền thời gian dao động mất $\dfrac{T}{2}$ , do đó theo trục phân bố thời gian:
$500\sqrt{2}=\dfrac{{{a}_{\max }}\sqrt{2}}{2}\to {{a}_{\max }}=1000$cm/s2 → ω2 = 250 → k = mω2 = 50 N/m
Câu 20.
Con lắc lò xo gồm một vật nhỏ có khối lượng 250g và lò xo nhẹ có độ cứng 100 N/m dao động điều hòa dọc theo trục Ox với biên độ 4 cm. Khoảng thời gian ngắn nhất để vận tốc của vật có giá trị từ – 40 cm/s đến 40$\sqrt{3}$ cm/s là
[A]. $\dfrac{\pi }{40}$s.
[B]. $\dfrac{\pi }{120}$s
[C]. $\dfrac{\pi }{20}$.
[D]. $\dfrac{\pi }{60}$s.
vmax = ωA = 80 cm/s.
Thời gian vận tốc dao động từ giá trị $-40=-\dfrac{{{v}_{\max }}}{2}$ đến $40\sqrt{3}=\dfrac{{{v}_{\max }}\sqrt{3}}{2}$ là $\dfrac{T}{12}+\dfrac{T}{6}=\dfrac{T}{4}=\dfrac{\pi }{40}$s

Câu 21.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 20 N/m dao động điều hoà với tần số 3 Hz. Trong một chu kì, khoảng thời gian để vật có độ lớn gia tốc không vượt quá $360\sqrt{3}$(cm/s2) là $\dfrac{2}{9}$s. Lấy π2 = 10. Năng lượng dao động là (Công thức năng lượng dao động CLLX: $\text{W}=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\dfrac{1}{2}k{{A}^{2}}$)
[A]. 4 mJ
[B]. 2 mJ
[C]. 6 mJ
[D]. 8 mJ
Diễn biến dao động của gia tốc trong một chu kì của vật như sau:
Các đoạn nét liền thời gian dao động mất $\dfrac{2}{9}s=\dfrac{2T}{3}$ , do đó theo trục phân bố thời gian:
$360\sqrt{3}=\dfrac{{{a}_{\max }}\sqrt{3}}{2}\to {{a}_{\max }}=720$cm/s2 → A = 2 cm → $W=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\dfrac{1}{2}k{{\text{A}}^{2}}=$ 4 mJ.

Câu 22.
Một vật dao động điều hòa với chu kì T trên trục Ox. Ở thời điểm t, vật có li độ x = 3 cm và chuyển động theo chiều dương. Thời điểm t + $\dfrac{T}{2}$ vật có li độ
[A]. 3 cm và chuyển động theo chiều dương.
[B]. -3 cm và chuyển động theo chiều âm.
[C]. -3 cm và chuyển động theo chiều dương.
[D]. 3 cm và chuyển động theo chiều âm.
$\Delta t=\dfrac{T}{2}$: hai thời điểm ngược pha, trạng thái dao động ngược nhau.
Câu 23.
Một vật dao động điều hòa với chu kì T trên trục Ox. Ở thời điểm t, vật có li độ x = 3 cm. Thời điểm t + $\dfrac{T}{4}$ vật có li độ x = – 4 cm. Biên độ dao động của vật là
[A]. 5 cm.
[B]. 6 cm.
[C]. 7 cm
[D]. 8 cm.
$\Delta t=\dfrac{T}{4}$: hai thời điểm vuông pha → $x_{1}^{2}+x_{2}^{2}={{A}^{2}}\to A=5\text{ }cm.$
Câu 24.
Một vật nhỏ dao động điều hoà dọc theo trục Ox với chu kì 0,5 s. Biết gốc tọa độ O ở vị trí cân bằng của vật. Tại thời điểm t, vật ở vị trí có li độ 5 cm, sau đó 2,25 s vật ở vị trí có li độ là
[A]. 10 cm.
[B]. – 5 cm.
[C]. 0 cm
[D]. 5 cm.
$\Delta t=2,25\text{s}=4T+\dfrac{T}{2}$: hai thời điểm ngược pha, trạng thái dao động ngược nhau.
Câu 25.
Vật dao động điều hòa với biên độ 10 cm, chu kì 0,5 s. Biết li độ của vật tại thời điểm t là – 6cm theo chiều âm, li độ của vật tại thời điểm t’ = t + 1,125(s) là
[A]. 5cm.
[B]. 8cm.
[C]. -8cm.
[D]. -5cm.
$\Delta t = 1,125\text{s}=2T+\dfrac{T}{4}$(2 thời điểm vuông pha): $x_{1}^{2}+x_{2}^{2}={{A}^{2}}\to {{x}_{2}}=\pm 8\text{ }cm.$
Cách 1: Sau 2T vật quay lại trạng thái tại t1: x = -6 cm (+), khoảng thời gian $\dfrac{T}{4}$tiếp theo vật dao động như sau
Ở t2, vật ở li độ x2 = -8 cm và theo chiều dương trục Ox .
Cách 2: Sử dụng công thức$\left\{ \begin{array}{l}{v_1} = \omega {x_2}\\{v_2} = – \omega {x_1}\end{array} \right.$; do v1 < 0 nên x2 < 0 → x2 = -8 cm và x1< 0 nên v2 > 0: vật đi theo chiều dương tại t2.
Câu 26.
Một chất điểm dao động điều hòa trên trục Ox với chu kì 6 s. Tại thời điểm t, vật có li độ 6 cm theo chiều âm. Trạng thái dao động của vật sau thời điểm đó 9 s là
[A]. Đi qua vị trí có li độ x = 3 cm và đang chuyển động theo chiều âm trục Ox.
[B]. Đi qua vị trí có li độ x = – 6 cm và đang chuyển động theo chiều dương của trục Ox.
[C]. Đi qua vị trí có li độ x = 6 cm và đang chuyển động theo chiều âm trục Ox.
[D]. Đi qua vị trí có li độ $x=-3\sqrt{3}$ cm và đang chuyển động theo chiều âm trục Ox.
$\Delta t=9\text{s}=T+\dfrac{T}{2}$: hai thời điểm ngược pha.
Câu 27.
Một vật dao động điều hòa với chu kì 1 s. Nếu tại thời điểm t1 vật li độ 2 cm thì ở thời điểm ${{t}_{2}}={{t}_{1}}+\dfrac{1}{4}\left( s \right)$vật có vận tốc là:
[A]. $-4\pi $cm/s.
[B]. $4\pi $cm/s.
[C]. $-\pi \sqrt{2}$cm/s.
[D]. $-\pi \sqrt{3}$cm/s.
$\Delta t=\dfrac{T}{4}$: vuông pha trường hợp 1 → ${{v}_{2}}=-\omega {{x}_{1}}=-4\pi $cm/s.
Câu 28.
Một vật dao động điều hòa với chu kì 1 s. Nếu tại thời điểm t1 vật li độ 2 cm thì ở thời điểm ${{t}_{2}}={{t}_{1}}+0,75s$vật có vận tốc là:
[A]. $-4\pi $cm/s.
[B]. $4\pi $cm/s.
[C]. $-\pi \sqrt{2}$cm/s.
[D]. $-\pi \sqrt{3}$cm/s.
$\Delta t=\dfrac{3T}{4}$: vuông pha trường hợp 2 → ${{v}_{2}}=\omega {{x}_{1}}=4\pi $cm/s.
Câu 29.
Một vật dao động điều hòa trên trục Ox với biên độ 25 cm và tần số f. Thời gian ngắn nhất để vận tốc của vật có giá trị từ – 7π cm/s đến 24π cm/s là $\dfrac{1}{4f}$. Lấy π2 = 10. Gia tốc cực đại của vật trong quá trình dao động là
[A]. 1,2 m/s2
[B]. 2,5 m/s2
[C]. 1,4 m/s2
[D]. 1,5 m/s2
$\Delta t=\dfrac{1}{4f}=\dfrac{T}{4}$: vuông pha → $v_{1}^{2}+v_{2}^{2}=v_{\max }^{2}\to {{v}_{\max }}=25\pi $cm/s → ω = π rad/s → amax = 2,5 m/s2.
Câu 30.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 100 N/m và vật nhỏ khối lượng m. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có li độ 5cm, ở thời điểm t +$\dfrac{T}{4}$vật có tốc độ 50cm/s. Giá trị của m bằng
[A]. 0,5 kg
[B]. 1,2 kg
[C]. 0,8 kg
[D]. 1,0 kg
$\Delta t=\dfrac{T}{4}$: vuông pha → $\left| {{v}_{2}} \right|=\omega \left| {{x}_{1}} \right|\to \omega =10$rad/s → $m=\dfrac{k}{{{\omega }^{2}}}$ = 1kg.
Câu 31.
Một con lắc dao động điều hòa theo phương ngang với chu kì T và biên độ 10 cm. Biết ở thời điểm t vật có li độ 6 cm, ở thời điểm t + $\dfrac{T}{2}$vật có tốc độ 80cm/s. Tần số góc của dao động bằng
[A]. 3 rad/s
[B]. 6 rad/s
[C]. 8 rad/s
[D]. 10 rad/s
$\Delta t=\dfrac{T}{2}$: ngược pha → ${{x}_{2}}=-{{x}_{1}}=-6$cm.
Lại có: $\text{x}_{2}^{2}+\dfrac{v_{2}^{2}}{{{\omega }^{2}}}={{A}^{2}}\to \omega =10$rad/s.
Câu 32.
Một con lắc dao động điều hòa theo phương ngang với chu kì T và biên độ 5 cm. Biết ở thời điểm t vật có tốc độ 20 cm/s, ở thời điểm t +$\dfrac{T}{4}$ gia tốc của vật có độ lớn 1 m/s2. Li độ tại thời điểm t có độ lớn bằng
[A]. 3 cm
[B]. 2,5 cm
[C]. $5\sqrt{2}$cm
[D]. $5\sqrt{3}$ cm
$\Delta t=\dfrac{T}{4}$: vuông pha → $\left| {{a}_{2}} \right|=\omega \left| {{x}_{1}} \right|\to \omega =5$rad/s.
Lại có: $\text{x}_{1}^{2}+\dfrac{v_{1}^{2}}{{{\omega }^{2}}}={{A}^{2}}\to \left| {{x}_{1}} \right|=3$cm
Câu 33.
Một con lắc dao động điều hòa theo trục Ox với tần số 10 rad/s. Biết ở thời điểm t vật có động lượng 0,4 kg.m/s, ở thời điểm t + $\dfrac{3T}{4}$ lực kéo về tác dụng lên vật có giá trị
[A]. 4 N
[B]. – 4 N
[C]. 5 N
[D]. -5 N
$\Delta t=\dfrac{3T}{4}$: vuông pha trường hợp 2 → ${{a}_{2}}=\omega {{v}_{1}}\text{ }hay\text{ m}{{a}_{2}}=\omega .m{{v}_{1}}\Leftrightarrow \text{ }{{\text{F}}_{2}}=\omega {{p}_{1}}=4N$.
Câu 34.
Một vật dao động điều hòa tuân theo qui luật x = 2cos(10t – π/6) cm. Nếu tại thời điểm t1 vật có vận tốc dương và gia tốc a1 = 1 m/s2 thì ở thời điểm. ${{t}_{2}}={{t}_{1}}+\dfrac{\pi }{20}$.(s) vật có gia tốc là:
[A]. $-\sqrt{3}$m/s2.
[B]. $-0,5\sqrt{3}$m/s2.
[C]. $0,5\sqrt{3}$m/s2.
[D]. $\sqrt{3}$m/s2.
$\Delta t=\dfrac{\pi }{20}=\dfrac{T}{4}$: vuông pha trường hợp 1
→ $a_{1}^{2}+a_{2}^{2}=a_{\max }^{2}\to {{a}_{2}}=\pm \sqrt{3}$m/s2;
Lại có: ${{v}_{1}}=\omega {{x}_{2}}\to \omega {{v}_{1}}={{\omega }^{2}}{{x}_{2}}\text{ hay }{{\text{a}}_{2}}=-\omega {{v}_{1}}<0\to {{a}_{2}}=-\sqrt{3}$m/s2.
Câu 35.
Một con lắc lò xo dao động điều hoà theo phương ngang. Biết ở thời điểm t vật có tốc độ 40 cm/s, sau đó ba phần tư chu kì gia tốc của vật có độ lớn 1,6π m/s2. Tần số dao động của vật bằng
[A]. 1 Hz
[B]. 2 Hz
[C]. 2,5 Hz
[D]. 4 Hz
$\Delta t=\dfrac{\pi }{20}=\dfrac{3T}{4}$: vuông pha → $\left| {{\text{a}}_{2}} \right|=\omega \left| {{v}_{1}} \right|\to \omega =4\pi $→ f = 2 Hz.
Câu 36.
Một con lắc lò xo nằm ngang gồm lò xo nhẹ có độ cứng k và vật nhỏ khối lượng 500 g. Con lắc dao động điều hòa với chu kì T. Biết ở thời điểm t vật có li độ 5 cm, ở thời điểm $\text{t + }\dfrac{\text{213T}}{\text{4}}$ vật có tốc độ 50 cm/s. Giá trị của k bằng
[A]. 40 N/m.
[B]. 50 N/m.
[C]. 100 N/m.
[D]. 200 N/m.
$\Delta t=\dfrac{213T}{4}=53T+\dfrac{T}{4}$: vuông pha → $\left| {{v}_{2}} \right|=\omega \left| {{x}_{1}} \right|\to \omega =10$→ k = mω2 = 50 N/m.
Câu 37.
Một vật dao động điều hoà với chu kì T biên độ 10 cm. Biết ở thời điểm t1 vật có li độ 5 cm và tốc độ v1, ở thời điểm t2 = t1 +$\dfrac{T}{4}$ vật có tốc độ $5\sqrt{3}$ cm/s. Giá trị v1 là
[A]. 5 cm/s
[B]. 10 cm/s
[C]. 15 cm/s
[D]. 20 cm/s
$\Delta t=\dfrac{T}{4}$: vuông pha → $\left| {{v}_{2}} \right|=\omega \left| {{x}_{1}} \right|\to \omega =\sqrt{3}$rad/s.
Lại có: $\text{x}_{1}^{2}+\dfrac{v_{1}^{2}}{{{\omega }^{2}}}={{A}^{2}}\to \left| {{v}_{1}} \right|=15$cm/s.
Câu 38.
Một vật nhỏ đang dao động điều hòa với chu kì 1 s. Tại thời điểm t1, vân tốc của vật có giá trị là là v1. Tại thời điểm t2 = t1 + 0,25 (s), vật có li độ 2 cm. Giá trị v1 là
[A]. 2π cm/s
[B]. -2π cm/s
[C]. -4π cm/s
[D]. 4π cm/s
$\Delta t=\dfrac{T}{4}$: vuông pha loại 1 → ${{v}_{1}}=\omega {{x}_{2}}=4\pi $cm/s.
Câu 39.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 50 N/m và vật nhỏ khối lượng m. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có li độ 5 cm, ở thời điểm $t+\dfrac{T}{2}$.vật có gia tốc 2 m/s2. Giá trị của m bằng
[A]. 1,25 kg
[B]. 1,20 kg
[C]. 1,5 kg
[D]. 1,0 kg
$\Delta t=\dfrac{T}{2}$: ngược pha → ${{x}_{2}}=-{{x}_{1}}=-5$cm.
Lại có ${{\text{a}}_{2}}=-{{\omega }^{2}}{{x}_{1}}\to {{\omega }^{2}}=40\to m=\dfrac{k}{{{\omega }^{2}}}=1,25$kg.
Câu 40.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng k và vật nhỏ khối lượng 500 g. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có vận tốc 10 cm/s, ở thời điểm t + $\dfrac{3T}{4}$vật có gia tốc 1 m/s2. Giá trị của k bằng
[A]. 50 N/m
[B]. 100 N/m
[C]. 150 N/m
[D]. 200 N/m
$\Delta t=\dfrac{3T}{4}$: vuông pha → $\left| {{a}_{2}} \right|=\omega \left| {{v}_{1}} \right|\to \omega =10\to k=50$N/m.
Câu 41.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 20 N/m và vật nhỏ khối lượng 500 g. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có gia tốc 1,2 m/s2, ở thời điểm t + $\dfrac{3T}{4}$vật có li độ -4 cm. Tốc độ trung bình con lắc trong một chu kì là
[A]. 1,27 m/s
[B]. 20,13 cm/s
[C]. 25,7 m/s
[D]. 1,96 m/s
Tại t1: ${{\text{a}}_{1}}=-{{\omega }^{2}}{{x}_{1}}\to {{x}_{1}}=-3$cm.
$\Delta t=\dfrac{3T}{4}$: vuông pha → $x_{1}^{2}+x_{2}^{2}={{A}^{2}}\to A=5\text{ cm}$ → ${{v}_{tb(T)}}=\dfrac{4\text{A}}{T}\approx 20,13$cm/s.
Câu 42.
Một con lắc lò xo nằm ngang dao động điều hòa xung quanh vị trí cân bằng và có độ lớn gia tốc cực đại là 4 m/s2. Tại thời điểm t vật ở li độ 1,5 cm thì sau đó một khoảng thời gian bằng 1/4 chu kỳ có tốc độ 15 cm/s. Tại t = 0 vật ở vị trí cân bằng và hướng theo chiều âm. Phương trình dao động của vật là
[A]. $x=8\cos (10t+\pi )\,cm$
[B]. $x=4\cos (10t-\dfrac{\pi }{2})\,cm$
[C]. $x=4\cos (10t+\dfrac{\pi }{2})\,cm$
[D]. $x=4\cos (10t+\dfrac{3\pi }{2})\,cm$
$\Delta t=\dfrac{T}{4}$: vuông pha → $\left| {{v}_{2}} \right|=\omega \left| {{x}_{1}} \right|\to \omega =10\to A=4\text{ cm}$
Tại t = 0: x = 0(-) → $\varphi =\dfrac{\pi }{2}$. Vậy phương trình dao động vật là $x=4\cos (10t+\dfrac{\pi }{2})\,cm$.
Câu 43.
Một vật dao động điều hòa xung quanh VTCB, tại thời điểm t vật ở vị trí có li độ 2 cm thì sau đó một khoảng thời gian bằng $\dfrac{3}{4}$ chu kì vật ở vị trí có li độ $-2\sqrt{3}$cm và có tốc độ 60 cm/s. Tại t = 0 vật ở vị trí có li độ $-2\sqrt{2}$cm hướng theo chiều dương. Phương trình dao động của vật là
[A]. $x=8\cos (30t-\dfrac{\pi }{4})\,cm$
[B]. $x=4\cos (30t-\dfrac{3\pi }{4})\,cm$
[C]. $x=8\cos (30t+\dfrac{3\pi }{4})\,cm$
[D]. $x=4\cos (30t+\dfrac{\pi }{4})\,cm$
$\Delta t=\dfrac{T}{4}$: vuông pha → $x_{1}^{2}+x_{2}^{2}={{A}^{2}}\to A=4\text{ }cm.$
$\text{x}_{2}^{2}+\dfrac{v_{2}^{2}}{{{\omega }^{2}}}={{A}^{2}}\to \omega =30$rad/s.
Tại t = 0: $\text{x}=-2\sqrt{2}(+)=-\dfrac{A\sqrt{2}}{2}(+)$ → $\varphi =-\dfrac{3\pi }{4}$.
Vậy phương trình dao động vật là $x=4\cos (30t-\dfrac{3\pi }{4})\,cm$.
Câu 44.
Một vật dao động điều hòa dọc theo trục Ox biên độ A. Δt là khoảng thời gian nhỏ nhất vật đi được quãng đường $A\sqrt{2}$. Tại thời điểm t vật cách vị trí cân bằng 3 cm và có tốc độ là là 8π cm/s2. Sau đó một khoảng thời gian 2015Δt gia tốc của vật có độ lớn 1,6 m/s2. Lấy π2 = 10. Giá trị của A là
[A]. 5 cm.
[B]. $5\sqrt{2}$ cm.
[C]. $4\sqrt{3}$ cm
[D]. 6 cm.
∆t là nghiệm phương trình: $A\sqrt{2}=2A\sin \dfrac{\pi \Delta t}{T}\to \Delta t=\dfrac{T}{4}$
$\text{x}_{1}^{2}+\dfrac{v_{1}^{2}}{{{\omega }^{2}}}={{A}^{2}}\to {{3}^{2}}+\dfrac{{{\left( 8\pi \right)}^{2}}}{{{\omega }^{2}}}={{A}^{2}}$(*)
$2015.\Delta t = 503T + \dfrac{3T}{4}$: vuông pha
→ $\left| {{a}_{2}} \right|=\omega \left| {{v}_{1}} \right|\to 160=\omega .8\pi \to \omega =2\pi $rad/s, thế vào (*) → A = 5 cm.
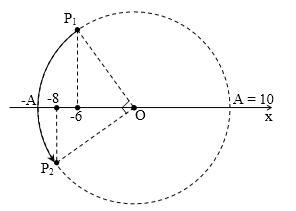
Câu 45.
Một vật dao động điều hòa trên trục Ox chu kì T. Ở thời điểm t và t + $\dfrac{T}{6}$, vật cùng có li độ 3 cm. Biên độ dao động của vật:
[A]. $2\sqrt{3}$ cm.
[B]. $4\sqrt{2}$ cm.
[C]. 6 cm.
[D]. $3\sqrt{3}$ cm.
Cứ mỗi chu kì, vật thực hiện 1 dao động toàn phần, tương ứng điểm pha chạy được 1 vòng (2π rad).
Vậy $\Delta t=\dfrac{T}{6}\to $điểm pha chạy được cung $\overset\frown{{{P}_{1}}{{P}_{2}}}=\dfrac{2\pi }{6}=\dfrac{\pi }{3}$ . Diễn biến dao động của vật ứng với pha chạy như sau:
Rõ ràng: ${{P}_{1}}\equiv -\dfrac{\pi }{6}$ và ${{P}_{2}}\equiv \dfrac{\pi }{6}$→ $3=\dfrac{A\sqrt{3}}{2}\to A=2\sqrt{3}$ cm.
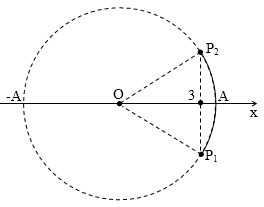
Câu 46.
Một vật dao động điều hòa trên trục Ox chu kì T. Ở thời điểm t, vật có li độ x = $2\sqrt{3}$ cm; sau đó khoảng thời gian $\dfrac{T}{3}$, vật có li độ x = $-2\sqrt{3}$ cm. Biên độ dao động của vật:
[A]. $4\sqrt{3}$ cm.
[B]. 12 cm.
[C]. 6 cm.
[D]. 4 cm.
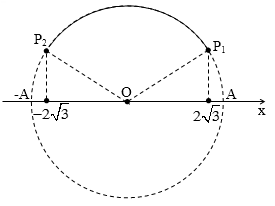
$\Delta t=\dfrac{T}{3}\to $điểm pha chạy được cung $\overset\frown{{{P}_{1}}{{P}_{2}}}=\dfrac{2\pi }{3}$ . Diễn biến dao động của vật ứng với pha chạy như sau:
Rõ ràng: ${{P}_{1}}\equiv \dfrac{\pi }{6}$ và ${{P}_{2}}\equiv \dfrac{5\pi }{6}$→ $2\sqrt{3}=\dfrac{A\sqrt{3}}{2}\to A=4$cm.
Câu 47.
Một dao động điều hòa mà 3 thời điểm liên tiếp t1, t2, t3 với t3 – t1 = 2(t3 – t2) li độ có giá trị là x1 = x2 = – x3 = 4 cm. Biên độ của dao động có giá trị là
[A]. $4\sqrt{2}\text{ cm}$
[B]. $8\sqrt{2}\text{ cm}$
[C]. 8 cm
[D]. $4\sqrt{3}\text{ cm}$
Diễn biến dao động của vật ứng với pha chạy như sau mới thỏa mãn:
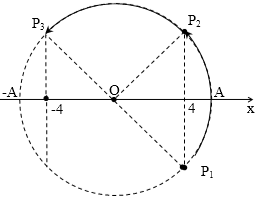
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{31}}=2\Delta {{t}_{21}}$, điểm pha chạy tròn đều nên: $\overset\frown{{{P}_{1}}{{P}_{3}}}=2\overset\frown{{{P}_{1}}{{P}_{2}}}\to \overset\frown{{{P}_{1}}{{P}_{2}}}=\dfrac{\pi }{2}\to {{P}_{1}}\equiv \dfrac{\pi }{4}$
→ $4=\dfrac{A\sqrt{2}}{2}\to A=4\sqrt{2}$ cm.
Câu 48.
Một vật dao động điều hòa với biên độ 8 cm. Ba thời điểm liên tiếp t1, t2, t3 với 3(t2 – t1) = t3 – t1 li độ có cùng độ lớn và giá trị thỏa mãn – x1 = x2 = x3 = a > 0. Giá trị của a là
[A]. $4\sqrt{2}\text{ cm}$
[B]. 4 cm
[C]. $4\sqrt{3}\text{ cm}$
[D]. 5,7 cm.
Diễn biến dao động của vật ứng với pha chạy như sau mới thỏa mãn:
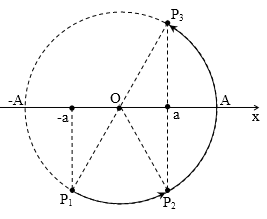
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{31}}=3\Delta {{t}_{21}}$, điểm pha chạy tròn đều nên: $\overset\frown{{{P}_{1}}{{P}_{3}}}=3\overset\frown{{{P}_{1}}{{P}_{2}}}\to \overset\frown{{{P}_{1}}{{P}_{2}}}=\dfrac{\pi }{3}\to {{P}_{3}}\equiv \dfrac{\pi }{3}$
→ $a=\dfrac{A}{2}=4$cm.
Câu 49.
Một dao động điều hòa mà 3 thời điểm liên tiếp t1, t2, t3 với t3 – t1 = 3(t3 – t2) li độ có giá trị là – x1 = x2 = x3 = $3\sqrt{3}$cm. Biên độ của dao động có giá trị là
[A]. $6\sqrt{2}\text{ cm}$
[B]. $\text{9 cm}$
[C]. 6 cm
[D]. $6\sqrt{3}\text{ cm}$
Diễn biến dao động của vật ứng với pha chạy như sau mới thỏa mãn:
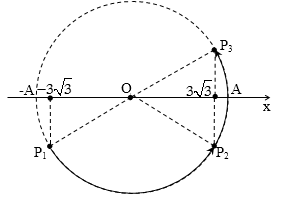
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{31}}=3\Delta {{t}_{32}}$, điểm pha chạy tròn đều nên: $\overset\frown{{{P}_{1}}{{P}_{3}}}=3\overset\frown{{{P}_{2}}{{P}_{3}}}\to \overset\frown{{{P}_{2}}{{P}_{3}}}=\dfrac{\pi }{3}\to {{P}_{3}}\equiv \dfrac{\pi }{6}$
→ $3\sqrt{3}=\dfrac{A\sqrt{3}}{2}\to A=6$cm.
Câu 50.
Một dao động điều hòa mà 3 thời điểm liên tiếp t1, t2, t3 với t3 – t1 = 3(t3 – t2) vận tốc có cùng độ lớn và thỏa mãn v1 = v2 = – v3 = 20 cm/s thì dao động đó có tốc độ cực đại là
[A]. 30 cm/s.
[B]. 20 cm/s.
[C]. 60 cm/s.
[D]. 40 cm/s.
Diễn biến dao động vận tốc v của vật ứng với pha vận tốc chạy như sau mới thỏa mãn:
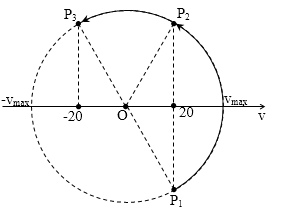
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{31}}=3\Delta {{t}_{32}}$, điểm pha chạy tròn đều nên: $\overset\frown{{{P}_{1}}{{P}_{3}}}=3\overset\frown{{{P}_{1}}{{P}_{2}}}\to \overset\frown{{{P}_{2}}{{P}_{3}}}=\dfrac{\pi }{3}\to {{P}_{2}}\equiv \dfrac{\pi }{3}$
→ $20=\dfrac{{{v}_{\max }}}{2}\to {{v}_{\max }}=40$cm/s.
Câu 51.
Một vật dao động điều hòa mà ba thời điểm liên tiếp t1, t2, t3 với${{t}_{3}}-{{t}_{1}}=2({{t}_{3}}-{{t}_{2}})=0,1\pi \ (s)$ gia tốc của vật có cùng độ lớn và thỏa mãn ${{a}_{1}}=-{{a}_{2}}=-{{a}_{3}}=1\ m/{{s}^{2}}$. Tốc độ dao động cực đại bằng
[A]. 20 cm/s
[B]. 40 cm/s
[C]. $10\sqrt{2}$cm/s.
[D]. $20\sqrt{2}$cm/s
Diễn biến dao động gia tốc của vật ứng với pha gia tốc chạy như sau mới thỏa mãn:
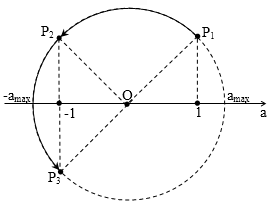
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{31}}=2\Delta {{t}_{32}}$, điểm pha chạy tròn đều nên: $\overset\frown{{{P}_{1}}{{P}_{3}}}=2\overset\frown{{{P}_{2}}{{P}_{3}}}\to \overset\frown{{{P}_{2}}{{P}_{3}}}=\dfrac{\pi }{2}\to {{P}_{1}}\equiv \dfrac{\pi }{4}$
→ $1=\dfrac{{{a}_{\max }}\sqrt{2}}{2}\to {{a}_{\max }}=\sqrt{2}$ m/s2.
Lại có: $\Delta {{t}_{31}}=\dfrac{T}{2}=0,1\pi \to T=0,2\pi \to \omega =10$rad/s → ${{v}_{\max }}=\dfrac{{{a}_{\max }}}{\omega }=10\sqrt{2}$ cm/s.
Câu 52.
Một vật dao động điều hòa với biên độ $6\sqrt{2}$cm, tần số góc ω > 10 rad/s. Trong quá trình dao động có ba thời điểm liên tiếp t1, t2 và t3 vật có cùng tốc độ $30\sqrt{6}$ cm/s. Biết t2 – t1 = 2(t3 – t2). Giá trị ω là
[A]. 20 rad/s.
[B]. $10\sqrt{6}$ rad/s.
[C]. $10\sqrt{3}$ rad/s.
[D]. 10 rad/s.
Diễn biến dao động vận tốc v của vật ứng với pha vận tốc chạy như sau mới thỏa mãn:
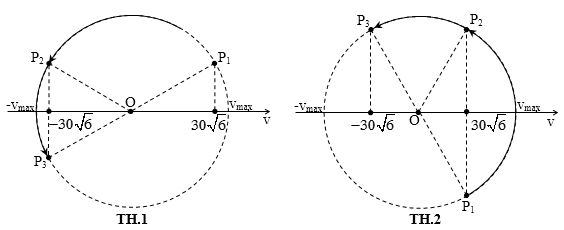
Dễ thấy: $\overset\frown{{{P}_{1}}{{P}_{3}}}=\pi $. Mà$\Delta {{t}_{21}}=2\Delta {{t}_{32}}$, điểm pha chạy tròng đều nên: $\overset\frown{{{P}_{1}}{{P}_{2}}}=2\overset\frown{{{P}_{2}}{{P}_{3}}}\to \overset\frown{{{P}_{1}}{{P}_{2}}}=\dfrac{2\pi }{3}$
TH1:$\to {{P}_{1}}\equiv \dfrac{\pi }{6}$→ $30\sqrt{6}=\dfrac{{{v}_{\max }}\sqrt{3}}{2}\to {{v}_{\max }}=60\sqrt{2}$cm/s → $\omega =10$ rad/s (loại).
TH2:$\to {{P}_{2}}\equiv \dfrac{\pi }{3}$→ $30\sqrt{6}=\dfrac{{{v}_{\max }}}{2}\to {{v}_{\max }}=60\sqrt{6}$cm/s → $\omega =10\sqrt{3}$ rad/s > 10 (nhận).
