Liên hệ giữa x v a p, F phần 4: thời điểm, thời gian, quãng đường
Câu 1.
Một chất điểm dao động điều hòa theo phương trình $x=10\cos \left( \pi t+\dfrac{\pi }{3} \right)$ (x tính bằng cm; t tính bằng s). Kể từ lúc t = 0, lần thứ 20 chất điểm có tốc độ 5π cm/s ở thời điểm
[A]. 9,83 s.
[B]. 18,5 s.
[C]. 19,5 s.
[D]. 19,66 s.
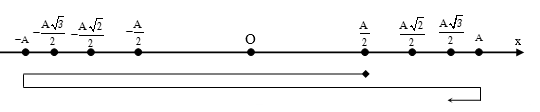
Dịch lại bài trên trục Ox: khi vật có tốc độ |v| = 5π cm/s = $\dfrac{{{v}_{\max }}}{2}$ ↔ x = $\pm \dfrac{A\sqrt{3}}{2}$
Dễ thấy một chu kì dao động, vật qua $x=\pm \dfrac{A\sqrt{3}}{2}$ 4 lần → Tách: 20 = 16 + 4.
Sau 4T, vật qua $x=\pm \dfrac{A\sqrt{3}}{2}$ 16 lần và quay lại trạng thái tại t = 0: $\text{x}=\dfrac{A}{2}(-)$, vật thực hiện 4 lần nữa theo trục phân bố thời gian mất: $\dfrac{11T}{12}$ .
Vậy thời điểm cần tìm là t’ = t + 4T + $\dfrac{11T}{12}$= 9,833 s.
Câu 2.
Một chất điểm dao động điều hòa theo phương trình $x=10\cos \left( \pi t+\dfrac{\pi }{3} \right)$ (x tính bằng cm; t tính bằng s). Kể từ lúc t = 0, lần thứ 20 vận tốc chất điểm có giá trị 5π cm/s ở thời điểm
[A]. 9,83 s.
[B]. 18,5 s.
[C]. 19,5 s.
[D]. 19,66 s.
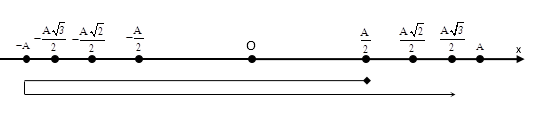
Dịch lại trên trục Ox: khi vật có vận tốc v = 5π cm/s > 0 ↔ $x=\pm \dfrac{A\sqrt{3}}{2}(+)$
Dễ thấy một chu kì dao động, vật qua$x=\pm \dfrac{A\sqrt{3}}{2}(+)$2 lần → Tách: 20 = 18 + 2.
Sau 9T, vật qua$x=\pm \dfrac{A\sqrt{3}}{2}(+)$18 lần và quay lại trạng thái tại t = 0: $\text{x}=\dfrac{A}{2}(-)$, vật thực hiện 2 lần nữa theo trục phân bố thời gian mất: $\dfrac{T}{3}+\dfrac{T}{4}+\dfrac{T}{6}$ .
Vậy thời điểm cần tìm là t’ = t + 9T + $\dfrac{T}{3}+\dfrac{T}{4}+\dfrac{T}{6}$= 19,5 s.
Câu 3.
Một vật nhỏ dao động điều hòa theo phương trình $x=6\cos \left( 5\pi t-\dfrac{\pi }{4} \right)$cm (t tính bằng s). Tính từ t = 0; thời điểm đầu tiên để vận tốc của vật có giá trị $-15\pi $cm/s là:
[A]. $\dfrac{1}{12}$s
[B]. x$\dfrac{1}{60}$ s
[C]. $\dfrac{1}{30}$s
[D]. 0,125 s.

Dịch lại trạng thái: Khi vật có vận tốc v = -15π cm/s = $-\dfrac{{{v}_{\max }}}{2}$ < 0 ↔ $x=\pm \dfrac{A\sqrt{3}}{2}(-)$
Tại t = 0: $\text{x}=\dfrac{A\sqrt{2}}{2}(+)$
Vậy thời điểm cần tìm là t’ = t + $\dfrac{T}{8}+\dfrac{T}{12}$= $\dfrac{1}{12}$s.
Câu 4.
Một vật dao động điều hòa theo phương trình x = 3cos(5πt – 0,5π) cm, t tính bằng giây. Thời điểm đầu tiên kể từ t = 0 gia tốc của vật có độ lớn cực đại là
[A]. 0,10 s.
[B]. 0,30 s.
[C]. 0,40 s
[D]. 0,20 s.

Dịch lại trạng thái: độ lớn gia tốc đạt cực đại tại hai biên.
Tại t = 0: $\text{x}=0(+)$
Vậy thời điểm cần tìm là t’ = t + $\dfrac{T}{4}$= 0,1 s.
Câu 5.
Một vật dao động điều hòa theo phương trình x = 3cos(5πt – 0,5π) cm, t tính bằng giây. Thời điểm đầu tiên kể từ t = 0 gia tốc của vật có giá trị cực đại là
[A]. 0,10 s.
[B]. 0,30 s.
[C]. 0,40 s.
[D]. 0,20 s.
Dịch lại trạng thái: gia tốc vật đạt giá trị cực đại tại biên âm: x = -A
Tại t = 0: $\text{x}=0(+)$
Vậy thời điểm cần tìm là t’ = t + $\dfrac{3T}{4}$= 0,3 s.

Câu 6.
Một vật dao động điều hòa theo phương trình x = 3cos(5πt – 0,5π) cm, t tính bằng giây. Lấy π2 = 10. Kể thời điểm ban đầu t = 0, thời điểm gia tốc của vật có giá trị bằng 3,75 m/s2 lần thứ 98 là
[A]. 19,43 s.
[B]. 19,57 s.
[C]. 19,23 s
[D]. 19,83 s.
Dịch lại trạng thái: vật có gia tốc a = -ω2x = 3,75 m/s2 ↔ $x=-1,5cm=-\dfrac{A}{2}$
Dễ thấy một chu kì dao động, vật qua $x=-\dfrac{A}{2}$2 lần → Tách: 98 = 96 + 2.
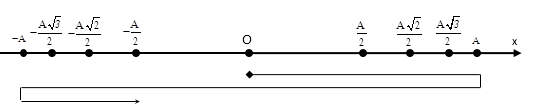
Sau 48T, vật qua $x=-\dfrac{A}{2}$ 96 lần và quay lại trạng thái tại t = 0: $\text{x}=0(+)$, vật thực hiện 2 lần nữa theo trục phân bố thời gian mất: $\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$ .
Vậy thời điểm cần tìm là t’ = t + 48T + $\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$= 19,57 s.
Câu 7.
Một vật nhỏ dao động điều hòa theo phương trình $x=5\cos \left( 2\pi t+\dfrac{\pi }{2} \right)$(cm) (t tính bằng s). Cho π2 = 10. Thời điểm lần thứ 10 vật có gia tốc -1 m/s2 là:
[A]. 4,583 s
[B]. 4,104 s
[C]. 4,917 s
[D]. 4,125 s.
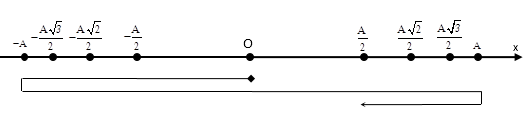
Dịch lại trạng thái: vật có gia tốc a = -ω2x = -1m/s2 ↔ $x=2,5cm=\dfrac{A}{2}$
Dễ thấy một chu kì dao động, vật qua$x=\dfrac{A}{2}$2 lần → Tách: 10 = 8 + 2.
Sau 4T, vật qua $x=\dfrac{A}{2}$8 lần và quay lại trạng thái tại t = 0: $\text{x}=0(-)$, vật thực hiện 2 lần nữa theo trục phân bố thời gian mất: $\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$ .
Vậy thời điểm cần tìm là t’ = 4T + $\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$= 4,917 s.
Câu 8.
Cho vật dao động điều hòa với phương trình $x=2\cos \left( 2\pi t+\dfrac{\pi }{3} \right)$cm. Cho π2 = 10. Vận tốc của vật sau khi vật đi được quãng đường 74,5cm tính từ thời điểm ban đầu là:
[A]. $-2\pi \sqrt{2}$cm/s
[B]. $2\pi \sqrt{7}$cm/s
[C]. $-2\pi \sqrt{7}$cm/s
[D]. $-\pi \sqrt{7}$cm/s
S = 74,5 cm = 9.4A + 1,25A (2,5cm)
Sau 9T vật đi được 9.4A và quay lại trạng thái tại t = 0: $\text{x}=\dfrac{A}{2}(-)$, vật đi tiếp 2,5 cm như sau
Dễ thấy vật qua vị trí $\text{x}=-1,5cm(-)$ → $v=-\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=-\pi \sqrt{7}$cm/s .

Câu 9.
Một chất điểm dao động điều hòa với phương trình $x=A\cos \left( 2\pi t+\dfrac{\pi }{3} \right)$ Kể từ thời điểm ban đầu t = 0 thời điểm vận tốc của chất điểm có giá trị bằng một nửa tốc độ cực đại lần thứ 8 là
[A]. 4,25 s.
[B]. 3,75 s.
[C]. 2 s.
[D]. 0,92 s.

Dịch lại trạng thái: Khi vật có vận tốc $v=\dfrac{{{v}_{\max }}}{2}>0$ ↔ $x=\pm \dfrac{A\sqrt{3}}{2}(+)$
Dễ thấy một chu kì dao động, vật qua$x=\pm \dfrac{A\sqrt{3}}{2}(+)$2 lần → Tách: 8 = 6 + 2.
Sau 3T, vật qua$x=\pm \dfrac{A\sqrt{3}}{2}(+)$6 lần và quay lại trạng thái tại t = 0: $\text{x}=\dfrac{A}{2}(-)$, vật thực hiện 2 lần nữa theo trục phân bố thời gian mất: $\dfrac{T}{3}+\dfrac{T}{4}+\dfrac{T}{6}$ .
Vậy thời điểm cần tìm là t’ = t + 3T + $\dfrac{T}{3}+\dfrac{T}{4}+\dfrac{T}{6}$= 3,75 s.
Câu 10.
Cho vật dao động điều hòa với phương trình $x=5\cos \left( 2\pi t+\dfrac{2\pi }{3} \right)$cm. Cho π2 = 10. Gia tốc của vật sau khi vật đi được quãng đường 64,5cm tính từ thời điểm ban đầu là
[A]. 1,2 m/s2
[B]. 0,8 m/s2
[C]. – 1,2 m/s2
[D]. – 0,8 m/s2
S = 64,5 cm = 3.4A + 4,5cm
Sau 3T vật đi được 3.4A và quay lại trạng thái tại t = 0: $\text{x}=-\dfrac{A}{2}(-)$, vật đi tiếp 4,5 cm như sau
Dễ thấy vật qua vị trí $\text{x}=-3cm(+)$ → $a=-{{\omega }^{2}}x=1,2$m/s2 .

Câu 11.
Một vật nhỏ dao động điều hòa theo phương trình $x=4\cos \left( 2t+\dfrac{\pi }{3} \right)$(cm) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 2 cm đến vị trí có gia tốc $-8\sqrt{3}$ cm/s là:
[A]. π/6 s
[B]. π/24 s
[C]. π/8 s
[D]. π/12 s

$a=-{{\omega }^{2}}x\leftrightarrow x=2\sqrt{3}$ cm
Vậy thời gian ngắn nhất cần tìm là $\dfrac{T}{12}=\dfrac{\pi }{12}s$ .
Câu 12.
Một vật nhỏ dao động điều hòa trên trục Ox. Khoảng thời gian từ khi vận tốc của vật có giá trị cực đại đến khi gia tốc của vật có giá trị cực đại là 2 s. Chu kì dao động là
[A]. 2,67 s.
[B]. 2 s.
[C]. 3 s.
[D]. 4 s.
Vận tốc có giá trị cực đại ↔ x = O (+)
Gia tốc có giá trị cực đại ↔ x = -A
Vậy thời gian ngắn nhất cần tìm là $\dfrac{3T}{4}=2s\to T=\dfrac{8}{3}s$ .

Câu 13.
Cho vật dao động điều hòa với phương trình $x=4\cos 5\pi t$cm. Cho π2 = 10. Vận tốc của vật sau khi vật đi được quãng đường 99 cm tính từ thời điểm ban đầu là
[A]. $5\sqrt{70}$cm/s
[B]. $25\sqrt{6}$cm/s
[C]. – $25\sqrt{6}$cm/s
[D]. -$5\sqrt{70}$cm/s
S = 99 cm = 6.4A + 3 cm
Sau 6T vật đi được 6.4A và quay lại trạng thái tại t = 0: $\text{x}=A$, vật đi tiếp 3 cm như sau

Dễ thấy vật qua vị trí $\text{x}=1cm(-)$ → $v=-\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=-25\sqrt{6}$cm/s .
Câu 14.
Một vật nhỏ dao động điều hòa theo phương trình $x=A\cos 4\pi t$ (t tính bằng s). Tính từ t = 0; khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là:
[A]. 0,083 s
[B]. 0,104 s
[C]. 0,167 s
[D]. 0,125 s.
Gia tốc có độ lớn bằng nửa độ lớn gia tốc cực đại: $\left| a \right|=\dfrac{{{\omega }^{2}}A}{2}\to \left| x \right|=\dfrac{A}{2}$
Thời điểm cần tìm là $\dfrac{T}{6}=\dfrac{1}{12}s$ .

Câu 15.
Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 10 cm với chu kì 2 s. Cho π2 = 10. Từ thời điểm vật qua vị trí có gia tốc -25 cm/s2 theo chiều âm đến khi vận tốc của vật đạt giá trị cực đại lần thứ 5, vật có tốc độ trung bình là
[A]. 12,33 cm/s.
[B]. 12,73 cm/s.
[C]. 10,09 cm/s.
[D]. 11,32 cm/s.

Vật theo chiều âm và có $a=-{{\omega }^{2}}x=-25cm/{{s}^{2}}\leftrightarrow x=\dfrac{A}{2}(-)$
Vận tốc đạt giá trị cực đại ↔ x = O(+)
Một chu kì, vật qua x = O(+) 1 lần. Tách 5 = 4 + 1.
Sau 4T, vật đi được 16A và qua x = O(+) 4 lần và trở lại trạng thái $x=\dfrac{A}{2}(-)$. Vật đi thêm 1 lần nữa mất $\dfrac{T}{3}+\dfrac{T}{4}$ và đi được thêm 2,5A
Vậy tốc độ trung bình vật trong quá trình này là ${{v}_{tb}}=\dfrac{S}{\Delta t}=\dfrac{\text{16A}+2,5\text{A}}{4T+\dfrac{T}{3}+\dfrac{T}{4}}=10,9$cm/s.
Câu 16.
Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là
[A]. 27,0 cm/s.
[B]. 26,7 cm/s.
[C]. 28,0 cm/s.
[D]. 27,3 cm/s.
Câu 17.
Một chất điểm dao động điều hòa. Biết thời gian ngắn nhất để vận tốc của vật giảm từ giá trị cực đại v0 = 10 cm/s để còn lại một nửa là 0,2π (s). Quỹ đạo dao động là
[A]. 6 cm.
[B]. 12 cm.
[C]. 24 cm.
[D]. 8 cm.
Vận tốc giảm từ cực đại còn một nửa là $\dfrac{T}{6}=0,2\pi $ (tương ứng vật đi từ VTCB đến $\dfrac{A\sqrt{3}}{2}$)$\to T=1,2\pi $
↔ ω = $\dfrac{5}{3}ra\text{d}/s$ → A = $\dfrac{{{v}_{\max }}}{\omega }=6cm$ → L = 12 cm.
Câu 18.
Một chất điểm dao động điều hòa. Biết thời gian ngắn nhất để vận tốc của vật giảm từ giá trị cực đại 8π cm/s về giá trị -4π cm/s là 0,2 s. Lấy π2 = 10. Gia tốc của vật có giá trị cực đại trong quá trình dao động là
[A]. 1,6 m/s2.
[B]. 3,2 m/s2.
[C]. 2,67 m/s2.
[D]. 1,67 cm/s2.

Dễ thấy: $0,2\text{s}=\dfrac{T}{3}\to T=0,6\text{s}$ →$\omega =\dfrac{10\pi }{3}$ → A = 2,4 cm → amax = 2,67 m/s2 .
Câu 19.
Một chất điểm dao động điều hòa có vận tốc cực đại 10π cm/s và gia tốc cực đại là 20π2 (cm/s2). Thời điểm ban đầu (t = 0), chất điểm có vận tốc -5π cm/s và gia tốc đang mang giá trị âm. Chất điểm có gia tốc bằng 10π2 (cm/s2) lần thứ 10 ở thời điểm
[A]. 4,583 s.
[B]. 4,676 s.
[C]. 8,533 s.
[D]. 9,567 s.

vmax = 10π cm/s = ωA; amax = 20π2 cm/s = ω2A → ω = 2π rad/s; A = 5 cm.
Tại t = 0: v = -5π cm/s < 0 → $x=\pm \dfrac{A\sqrt{3}}{2}(-)$,
mà a < 0 → $x=\dfrac{A\sqrt{3}}{2}(-)$
Gia tốc a = 10π2 ↔ $x=-\dfrac{A}{2}$ .
Dễ thấy mỗi chu kì vật qua $x=-\dfrac{A}{2}$2 lần, do đó, tách 10 = 8 + 2
Vậy sau 4T vật qua $x=-\dfrac{A}{2}$8 lần và quay lại trạng thái tại t = 0: $x=\dfrac{A\sqrt{3}}{2}(-)$, vật đi qua 2 lần nữa theo diễn biến trục thời gian bên dưới mất $\dfrac{T}{6}+\dfrac{T}{4}+\dfrac{T}{6}$
Vậy thời điểm cần tìm là t’ = t + 4T +$\dfrac{T}{6}+\dfrac{T}{4}+\dfrac{T}{6}$= 4,583 s .
Câu 20.
Một con lắc lò xo dao động điều hòa trên trục Ox với phương trình dao động: $x=A\cos \left( \omega t-\dfrac{\pi }{6} \right)$. Biết rằng cứ sau khoảng thời gian ngắn nhất 0,25 s thì vật lại cách vị trí cân bằng một đoạn d như cũ (d < A). Thời điểm vận tốc v và li độ x của vật nhỏ thỏa mãn v = ω|x| lần thứ 2018 kể từ thời điểm ban đầu là
[A]. 2017,1333 s.
[B]. 1008,5667 s.
[C]. 1007,3421 s.
[D]. 1008,9583 s.

Ta biết: cứ sau $\dfrac{T}{4}$ thì vật lại qua các vị trí $\text{x}=\pm \dfrac{A\sqrt{2}}{2}$ thỏa mãn đề bài, do đó $\dfrac{T}{4}=0,25\text{s}$. Vậy T = 1s!
Khi v = ω|x| > 0 → ${{\text{x}}^{2}}+\dfrac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\to x=\pm \dfrac{A\sqrt{2}}{2}(+)$.
Dễ thấy mỗi chu kì vật qua $x=\pm \dfrac{A\sqrt{2}}{2}(+)$$x=-\dfrac{A}{2}$2 lần, do đó, tách 2018 = 2016 + 2
Vậy sau 1008T vật qua $x=\pm \dfrac{A\sqrt{2}}{2}(+)$2016 lần và quay lại trạng thái tại t = 0: $x=\dfrac{A\sqrt{3}}{2}(+)$, vật đi qua 2 lần nữa theo diễn biến trục thời gian bên dưới mất $\dfrac{T}{12}+\dfrac{T}{2}+\dfrac{T}{4}+\dfrac{T}{8}$
Vậy thời điểm cần tìm là t’ = t + 1008T +$\dfrac{T}{12}+\dfrac{T}{2}+\dfrac{T}{4}+\dfrac{T}{8}$= 1008,9583 s .
Câu 21.
Một con lắc lò xo dao động điều hòa trên trục Ox với chu kì 3 s. Tại thời điểm ban đầu (t = 0), vật ở vị trí có gia tốc đạt giá trị cực đại. Thời điểm vận tốc v và li độ x của vật nhỏ thỏa mãn v = ωx lần thứ 2018 kể từ thời điểm ban đầu là
[A]. 1513,125 s.
[B]. 3026,625s.
[C]. 1008,875 s.
[D]. 2017,2667 s.

Tại t = 0 vật có gia tốc cực đại ↔ x = -A
Khi v = ωx (v và x cùng dấu) → ${{\text{x}}^{2}}+\dfrac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\to x=\dfrac{A\sqrt{2}}{2}(+)\text{ or}-\dfrac{A\sqrt{2}}{2}(-)$
Dễ thấy mỗi chu kì vật qua $x=\dfrac{A\sqrt{2}}{2}(+)\text{ or}-\dfrac{A\sqrt{2}}{2}(-)$2 lần, do đó, tách 2018 = 2016 + 2.
Vậy sau 1008T vật qua $x=\dfrac{A\sqrt{2}}{2}(+)\text{ or}-\dfrac{A\sqrt{2}}{2}(-)$2016 lần và quay lại trạng thái tại t = 0: $x=-A$, vật đi qua 2 lần nữa theo diễn biến trục thời gian bên dưới mất $\dfrac{T}{2}+\dfrac{T}{4}+\dfrac{T}{8}$
Vậy thời điểm cần tìm là t’ = t + 1008T +$\dfrac{T}{2}+\dfrac{T}{4}+\dfrac{T}{8}$= 3026,625 s .
Câu 22.
Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc ω. Vật nhỏ của con lắc có khối lượng 450 g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 1,475 s, vận tốc v và li độ x của vật nhỏ thỏa mãn $v=\omega \left| x \right|\sqrt{3}$ lần thứ 10. Lấy π2 = 10. Độ cứng của lò xo là
[A]. 100 N/m.
[B]. 150 N/m.
[C]. 200 N/m.
[D]. 250 N/m.

Khi $v=\omega \left| x \right|\sqrt{3}$ (v >0) → ${{\text{x}}^{2}}+\dfrac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\to x=\pm \dfrac{A}{2}(+)$
Dễ thấy mỗi chu kì vật qua $x=\pm \dfrac{A}{2}(+)$2 lần, do đó, tách 10 = 8 + 2
Vậy sau 4T vật qua $x=\pm \dfrac{A}{2}(+)$8 lần và quay lại trạng thái tại t = 0: x = O(+), vật đi qua 2 lần nữa theo diễn biến trục thời gian bên dưới mất $\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$
Thời điểm t = 1,475s = 4T +$\dfrac{T}{4}+\dfrac{T}{2}+\dfrac{T}{6}$↔ T = 0,3 s → $\omega =\dfrac{20\pi }{3}$ → k = mω2 = 200N/m .
Câu 23.
Con lắc gồm vật nhỏ có khối lượng m = 250 g và lò xo nhẹ có độ cứng k = 100 N/m đang dao động điều hoà. Chọn gốc thời gian t = 0 khi vật nhỏ qua vị trí cân bằng theo chiều dương. Trong khoảng thời gian $\dfrac{\pi }{20}$ (s) đầu tiên kể từ t = 0, vật đi được quãng đường 4 cm. Vận tốc của vật tại thời điểm $\dfrac{\pi }{15}$ (s) là
[A]. v = $20\sqrt{3}$ cm/s.
[B]. v = $-20\sqrt{3}$ cm/s.
[C]. v = 40 cm/s.
[D]. v = − 20 cm/s.

$T=2\pi \sqrt{\dfrac{m}{k}}=\dfrac{\pi }{10}s$
Kể từ t = 0: x= O(+), sau $\dfrac{\pi }{20}s=\dfrac{T}{2}$ vật đi được 2A = 4 cm → A = 2 cm.
Sau $\dfrac{\pi }{15}s=\dfrac{2T}{3}=\dfrac{T}{4}+\dfrac{T}{4}+\dfrac{T}{6}$, vật thực hiện diễn biến dao động như sau:
Vậy tại thời điểm $\dfrac{\pi }{15}$ s, vật có $\text{x}=-\dfrac{A\sqrt{3}}{2}(-)$ → $v=-\dfrac{{{v}_{\max }}}{2}=-20$ cm/s.
Câu 24.
Một vật dao động điều hoà xung quanh vị trí cân bằng O. Ban đầu vật đi qua O theo chiều dương. Sau thời gian ${{t}_{1}}=\dfrac{\pi }{20}s$ vật chưa đổi chiều chuyển động và vận tốc giảm $\sqrt{2}$ lần. Sau thời gian t2 = 0,5π (s) tính từ thời điểm ban đầu vật đã đi được 20 cm. Vận tốc ban đầu v0 của vật là
[A]. 20 cm/s
[B]. 25 cm/s
[C]. 3 cm/s
[D]. 40 cm/s
Câu 25.
Trong khoảng thời gian từ t = τ đến t = 2τ, vận tốc của một vật dao động điều hòa tăng từ 0,5vM đến vM rồi giảm về $\dfrac{{{v}_{M}}\sqrt{3}}{2}$. Ở thời điểm t = 0, li độ của vật là:
[A]. ${{x}_{o}}=-\dfrac{\tau .{{v}_{M}}}{\pi }.$
[B]. ${{x}_{o}}=+\dfrac{\tau .{{v}_{M}}}{\pi }.$
[C]. ${{x}_{o}}=+\dfrac{\tau .{{v}_{M}}}{2\pi }.$
[D]. ${{x}_{o}}=-\dfrac{\tau .{{v}_{M}}}{2\pi }.$

$v=0,5{{v}_{M}}\to x=\pm \dfrac{A\sqrt{3}}{2}$
$v={{v}_{M}}\dfrac{\sqrt{3}}{2}\to x=\dfrac{A}{2}$
Vậy khi vận tốc tăng từ 0,5vM đến vM rồi giảm về $\dfrac{{{v}_{M}}\sqrt{3}}{2}$ thì diễn biến vật dao động như sau:
Theo đó: t2 – t1 = $\tau $ = $\dfrac{T}{4}$ → $T=4\tau $
Tại t1 =$\tau $: $\text{x}=-\dfrac{A\sqrt{3}}{2}(+)$ →${{\phi }_{\tau }}=\omega \tau +\varphi =-\dfrac{5\pi }{6}\to \varphi =-\dfrac{4\pi }{3}\equiv \dfrac{2\pi }{3}$ →${{\text{x}}_{0}}=-\dfrac{A}{2}(-)$
Mà $\text{A}=\dfrac{{{v}_{M}}}{\omega }=\dfrac{T{{v}_{M}}}{2\pi }=\dfrac{2\tau {{v}_{M}}}{\pi }$→${{\text{x}}_{0}}=-\dfrac{\tau {{v}_{M}}}{\pi }$ .
Câu 26.
Một vật dao động điều hòa tại thời điểm ban đầu vật qua vị trí cân bằng theo chiều dương. Đến thời điểm t1= $\dfrac{1}{3}$ s vật chưa đổi chiều chuyển động và có vận tốc bằng $\dfrac{\sqrt{3}}{2}$ vận tốc ban đầu. Đến thời điểm t2= $\dfrac{5}{3}$s vật đã đi được quãng đường 6 cm . Vận tốc ban đầu của vật là:
[A]. – 2π cm/s.
[B]. π cm/s.
[C]. 2π cm/s.
[D]. 3π cm/s.
Câu 27.
Một vật dao động điều hòa với biên độ 12cm. Trong một chu kì, thời gian vật có tốc độ lớn hơn một giá trị vo nào đó là 2s. Tốc độ trung bình khi đi một chiều giữa hai vị trí có cùng tốc độ vo ở trên là $12\sqrt{3}$ cm/s. Tốc độ vo là:
[A]. $4\pi \sqrt{3}$ cm/s
[B]. 8π cm/s
[C]. 4π cm/s
[D]. $4\pi \sqrt{2}$ cm/s
Câu 28.
Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng 0 tại hai thời điểm t1 = 2,8s và t2 = 3,6s; vận tốc trung bình trong khoảng thời gian đó là 10 cm/s. Biên độ dao động là
[A]. 4 cm
[B]. 5 cm
[C]. 2 cm
[D]. 3 cm
Vận tốc vật bằng 0 tại 2 biên, do đó: ${{v}_{tb}}=\dfrac{S}{\Delta t}=\dfrac{2\text{A}}{{{t}_{2}}-{{t}_{1}}}\to A$ = 4 cm
Câu 29.
Một vật dao động với biên độ 10cm. Trong một chu kì, thời gian vật có tốc độ lớn hơn một giá trị vo nào đó là 1s. Tốc độ trung bình khi đi một chiều giữa hai vị trí có cùng tốc độ vo ở trên là 20 cm/s. Tốc độ vo là:
[A]. 10,47 cm/s
[B]. 14,8 cm/s
[C]. 11,54 cm/s
[D]. 18,14 cm/s
Câu 30.
Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng không tại hai thời điểm liên tiếp t1 = 1,75 s và t2 = 2,5s, tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0, vận tốc dao động là v0 (cm/s) và li độ x0 (cm) của vật thỏa mãn hệ thức
[A]. x0v0 = − 12π$\sqrt{3}$.
[B]. x0.v0 = 12π$\sqrt{3}$.
[C]. x0v0 = − 4π$\sqrt{3}$.
[D]. x0v0 = 4π$\sqrt{3}$.
Câu 31.
Một vật dao động điều hòa với biên độ A trên trục Ox. Xét quá trình vật đi từ vị trí cân bằng ra biên, khi vật rời khỏi vị trí cân bằng đoạn S thì tốc độ của vật là $\text{a}\sqrt{8}$ (m/s), vật đi thêm đoạn S nữa thì tốc độ giảm còn $\text{a}\sqrt{5}$ (m/s), vật đi thêm đoạn S nữa thì tốc độ của vật là (biết 3S < A)
[A]. 2a (m/s).
[B]. 0
[C]. 3a (m/s).
[D]. a (m/s).
Sử dụng công thức độc lập thời gian x và v cho các vị trí ta có:
$\left. {\left\{ \begin{array}{l} \left. \begin{array}{l} {S^2} + \dfrac{{8{{\rm{a}}^2}}}{{{\omega ^2}}} = {A^2}\\ 4{S^2} + \dfrac{{5{{\rm{a}}^2}}}{{{\omega ^2}}} = {A^2} \end{array} \right\} \to {S^2} = \dfrac{{{{\rm{a}}^2}}}{{{\omega ^2}}};{A^2} = \dfrac{{{\rm{9}}{{\rm{a}}^2}}}{{{\omega ^2}}}\\ 9{S^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \end{array} \right.} \right\} \to v = 0$ (vật tới biên sau khi đi 3S) .
Câu 32.
Vật dao động điều hòa với vận tốc cực đại là vM Trong khoảng thời gian từ t = τ đến t = 2τ, vận tốc của một vật dao động điều hòa giảm từ 0,5vM về -0,5vM. Ở thời điểm t = 0, li độ của vật là:
[A]. ${{x}_{o}}=-\dfrac{\tau .{{v}_{M}}}{\pi }.$
[B]. ${{x}_{o}}=+\dfrac{\tau .{{v}_{M}}}{\pi }.$
[C]. ${{x}_{o}}=+\dfrac{\tau .{{v}_{M}}}{2\pi }.$
[D]. 0
Theo trục phân bố thời gian của vận tốc, vận tốc khi giảm từ 0,5vM về -0,5vM mất $\dfrac{T}{6}=\tau \to T=6\tau $.
Tại t1 = $\tau =\dfrac{T}{6}$, vật có v = 0,5vM > 0 (vật đi theo chiều dương) → $\text{x}=\pm \dfrac{A\sqrt{3}}{2}$ (+), do vận tốc của vật ngay sau đó giảm nên $\text{x}=\dfrac{A\sqrt{3}}{2}(+)$→ ${{\phi }_{\tau }}=\omega \tau +\varphi =-\dfrac{\pi }{6}\to \varphi =\dfrac{-\pi }{2}$ → Tại t = 0, vật đi qua VTCB (+).
Câu 33.
Một vật dao động điều hòa với chu kì T, trên một đoạn thẳng, giữa hai điểm biên M và N. Chọn chiều dương từ M đến N, gốc tọa độ tại vị trí cân bằng O, mốc thời gian t = 0 là lúc vật đi qua trung điểm I của đoạn MO theo chiều dương. Gia tốc của vật bằng không lần thứ nhất vào thời điểm
[A]. t = $\dfrac{T}{6}$.
[B]. t = $\dfrac{T}{3}$.
[C]. t = $\dfrac{T}{12}$.
[D]. t = $\dfrac{T}{4}$ .
Câu 34.
Hai chất điểm 1 và 2 dao động điều hoà trên một trục Ox với cùng biên độ. Tại thời điểm t = 0, hai chất điểm đều đi qua vị trí cân bằng theo chiều dương. Chu kì dao động của chất điểm 1 là T và gấp bốn làn chu kì dao động của chất điểm 2. Tỉ số vận tốc của chất điểm 1 và chất điểm 2 ở thời điểm $\dfrac{T}{12}$ là
[A]. $\dfrac{\sqrt{3}}{2}$
[B]. $\sqrt{3}$
[C]. $-\dfrac{\sqrt{3}}{2}$
[D]. $-\dfrac{\sqrt{3}}{4}$
T1 = T; T2 = 0,25T
Sau $\dfrac{T}{12}=\dfrac{{{T}_{1}}}{12}$, theo trục thời gian vật 1 đi từ VTCB tới ${{\text{x}}_{1}}=\dfrac{A}{2}(+)\to {{v}_{1}}=\dfrac{{{\omega }_{1}}A\sqrt{3}}{2}$
Sau $\dfrac{T}{12}=\dfrac{{{T}_{2}}}{3}$, theo trục thời gian vật 2 đi từ VTCB ra biên dương rồi quay lại ${{\text{x}}_{2}}=\dfrac{A\sqrt{3}}{2}(-)\to {{v}_{2}}=-\dfrac{{{\omega }_{2}}A}{2}$
Vậy $\dfrac{{{v}_{1}}}{{{v}_{2}}}=-\dfrac{{{\omega }_{1}}\sqrt{3}}{{{\omega }_{2}}}=-\dfrac{{{T}_{2}}\sqrt{3}}{{{T}_{1}}}=-\dfrac{\sqrt{3}}{4}$.
dạ cho em hỏi câu 9 là bị sai đúng không ạ. t = 3T + T/12 +T/2 + T/6 chứ ạ