Quãng đường lớn nhất nhỏ nhất dao động điều hòa
Câu 1.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ A và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{4}$, quãng đường lớn nhất mà vật có thể đi được là
[A]. A
[B]. $\dfrac{3A}{2}$.
[C]. $A\sqrt{3}$.
[D]. $A\sqrt{2}$
$\Delta t{\rm{ }} = \dfrac{T}{4} \to {S_{\max }} = 2A\sin \dfrac{{\pi \Delta t}}{T} = 2A\sin \dfrac{\pi }{4} = A\sqrt 2 $
Câu 2.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ A và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{3}$, quãng đường nhỏ nhất mà vật có thể đi được là
[A]. A.
[B]. $\dfrac{3A}{2}$.
[C]. $A\sqrt{3}$.
[D]. $A\sqrt{2}$
$\Delta t = \dfrac{T}{3} \Rightarrow {S_{\min }} = 2A\left( {1 – \cos \dfrac{{\pi \Delta t}}{T}} \right) = 2A\left( {1 – \cos \dfrac{\pi }{3}} \right) = A$
Câu 3.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ 4 cm và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{8}$, quãng đường lớn nhất mà vật có thể đi được là
[A]. $4\sqrt 2 {\rm{ }}cm$
[B]. 3,06 cm.
[C]. $4\sqrt 3 {\rm{ cm}}$
[D]. 1,53 cm .
$\Delta t = \dfrac{T}{8} \Rightarrow {S_{\max }} = 2A\sin \dfrac{{\pi \Delta t}}{T} = 2A\sin \dfrac{\pi }{8} = 3,06 (cm)$
Câu 4.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ A và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{6}$, tỉ số quãng đường lớn nhất, nhỏ nhất mà vật có thể đi được là
[A]. 2
[B]. $2+\sqrt{3}$.
[C]. $2+\sqrt{2}$.
[D]. 3
\[\Delta t = \dfrac{T}{6} \Rightarrow \dfrac{{{S_{\max }}}}{{{S_{\min }}}} = \dfrac{{2A\sin \dfrac{{\pi \Delta t}}{T}}}{{2A\left( {1 – \cos \dfrac{{\pi \Delta t}}{T}} \right)}} = \dfrac{{2A\sin \dfrac{\pi }{6}}}{{2A\left( {1 – \cos \dfrac{\pi }{6}} \right)}} = 2 + \sqrt 3 \]
Câu 5.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ 10 cm và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{5}$, quãng đường lớn nhất mà vật có thể đi được gần giá trị nào nhất
[A]. 8 cm
[B]. 12 cm
[C]. 16 cm
[D]. 20 cm
$\Delta t = \dfrac{T}{5} \Rightarrow {S_{\max }} = 2A\sin \dfrac{{\pi \Delta t}}{T} = 2A\sin \dfrac{\pi }{5} = 11,76 (cm)$
Câu 6.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ 8 cm và chu kỳ T. Trong khoảng thời gian $\dfrac{T}{7}$, quãng đường nhỏ nhất mà vật có thể đi được gần giá trị nào nhất
[A]. 2 cm
[B]. 2,5 cm
[C]. 1,5 cm
[D]. 1 cm
$\Delta t = \dfrac{T}{7} \Rightarrow {S_{\min }} = 2A\left( {1 – \cos \dfrac{{\pi \Delta t}}{T}} \right) = 2A\left( {1 – \cos \dfrac{\pi }{7}} \right) = 1,58cm$
Câu 7.
Một vật dao động điều hòa trên một quỹ đạo là một đoạn thẳng dài 12 cm, với chu kì 2 s. Quãng đường dài nhất vật đi được trong thời gian 0,5 s là
[A]. 9,48 cm
[B]. 8,49 cm
[C]. 16,97 cm
[D]. 6 cm.
A = L/2 = 6 cm; $\Delta t=0,5s=\dfrac{T}{4}\Rightarrow {{S}_{\min }}=2A\sin \dfrac{\pi }{4}=8,49\left( cm \right)$ .
Câu 8.
Một vật dao động điều hoà với phương trình x = Acos(4πt +$\dfrac{\pi }{3}$). Quãng đường lớn nhất mà vật đi được trong khoảng thời gian \[\dfrac{1}{6}\] s là $4\sqrt{3}$cm. Biên độ dao động A là
[A]. $4\sqrt{3}$cm
[B]. $3\sqrt{3}$cm
[C]. 4 cm
[D]. $2\sqrt{3}$cm
T = 0,5 s; $\Delta t\text{ }=\dfrac{1}{6}s=\dfrac{T}{3}$ → ${{S}_{\max }}=2A\sin \dfrac{\pi }{3}=A\sqrt{3}=4\sqrt{3}$cm. → A = 4 cm
Câu 9.
Một vật dao động điều hoà với phương trình x = 4cos(4πt +$\dfrac{\pi }{3}$). Tính quãng đường lớn nhất mà vật đi được trong khoảng thời gian \[\dfrac{1}{6}\] s là
[A]. $4\sqrt{3}$cm.
[B]. $3\sqrt{3}$cm
[C]. $\sqrt{3}$cm
[D]. $2\sqrt{3}$cm
T = 0,5 s; ∆t = $\dfrac{1}{6}s$= $\dfrac{T}{3}$ → ${{S}_{\max }}=2A\sin \dfrac{\pi }{3}=A\sqrt{3}=4\sqrt{3}$cm
Câu 10.
Một vật dao động điều hòa với chu kì bằng 2 s và biên độ A. Quãng đường dài nhất vật đi được trong thời gian $\dfrac{1}{3}$ s là
[A]. 2A/3
[B]. A/2.
[C]. A
[D]. 3A/2.
T = 2 s; ∆t = $\dfrac{1}{3}s$= $\dfrac{T}{6}$ → ${{S}_{\max }}=2A\sin \dfrac{\pi }{6}=A$.
Câu 11.
Một chất điểm dao động điều hòa, tỉ số giữa quãng đường lớn nhất và nhỏ nhất mà chất điểm đi được trong $\dfrac{1}{4}$ chu kì là
[A]. \[\sqrt{2}.\]
[B]. \[2\sqrt{2}.\]
[C]. \[\sqrt{2}+1.\]
[D]. \[\sqrt{2}+2.\]
∆t = $\dfrac{T}{4}$ → \[\dfrac{{{S}_{\max }}}{{{S}_{\min }}}=\dfrac{2A\sin \dfrac{\pi \Delta t}{T}}{2A\left( 1-\cos \dfrac{\pi \Delta t}{T} \right)}=\dfrac{2A\sin \dfrac{\pi }{4}}{2A\left( 1-\cos \dfrac{\pi }{4} \right)}=1+\sqrt{2}\].
Câu 12.
Một vật dao động điều hoà dọc theo trục Ox, quanh vị trí cân bằng O với biên độ A và chu kỳ T. Trong khoảng thời gian $\dfrac{5T}{3}$, quãng đường lớn nhất mà vật có thể đi được là
[A]. 7A.
[B]. $\dfrac{15A}{2}$.
[C]. $6A\sqrt{3}$.
[D]. $7A\sqrt{2}$
∆t =$\dfrac{5T}{3}=3.\dfrac{T}{2}+\dfrac{T}{6}$ → ${{S}_{\max }}=6A+{{S}_{\max \left( \dfrac{T}{6} \right)}}=6A+2A\sin \dfrac{\pi }{6}=7A$.
Câu 13.
Một vật dao động điều hoà với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t =$\dfrac{3T}{4}$, quãng đường nhỏ nhất mà vật đi được là
[A]. \[4A-A\sqrt{2}\]
[B]. \[A+A\sqrt{2}\]
[C]. \[2A+A\sqrt{2}\]
[D]. \[2A-A\sqrt{2}\]
∆t =$\dfrac{3T}{4}=\dfrac{T}{2}+\dfrac{T}{4}$ → ${{S}_{\min }}=2A+{{S}_{\min \left( \dfrac{T}{4} \right)}}=2A+2A\left( 1-\cos \dfrac{\pi }{4} \right)=4A-A\sqrt{2}$.
Câu 14.
Một chất điểm dao động điều hòa với chu kỳ T. Trong quá trình dao động, tỉ số giữa tốc độ trung bình nhỏ nhất và tốc độ trung bình lớn nhất của chất điểm trong cùng khoảng thời gian \[\dfrac{2T}{3}\] là
[A]. \[5-3\sqrt{2}.\]
[B]. \[\dfrac{4-\sqrt{3}}{3}.\]
[C]. \[\sqrt{2}-1.\]
[D]. \[\dfrac{\sqrt{3}}{3}.\]
∆t =$\dfrac{2T}{3}=\dfrac{T}{2}+\dfrac{T}{6}$ → \[\dfrac{{{v}_{tb\left( \dfrac{2T}{3} \right)-\min }}}{{{v}_{tb\left( \dfrac{2T}{3} \right)-\max }}}=\dfrac{{{S}_{\min \left( \dfrac{2T}{3} \right)}}}{{{S}_{\max \left( \dfrac{2T}{3} \right)}}}=\dfrac{2A+2A\left( 1-\cos \dfrac{\pi }{6} \right)}{2A+2A\sin \dfrac{\pi }{6}}=\dfrac{4-\sqrt{3}}{3}\].
Câu 15.
Cho vật dao động điều hòa biên độ A, chu kì T. Quãng đường lớn nhất mà vật đi được trong khoảng thời gian 5T/4 là
[A]. 2,5 A
[B]. 5A
[C]. $A\left( 4+\sqrt{3} \right)$.
[D]. $A\left( 4+\sqrt{2} \right)$.
∆t =$1,25T=2.\dfrac{T}{2}+\dfrac{T}{4}$ → \[{{S}_{\max \left( 1,25T \right)}}=4A+A\sqrt{2}\].
Câu 16.
Một vật dao động điều hòa với chu kỳ 2 s, biên độ 4cm. Quãng đường dài nhất vật đi được trong khoảng thời gian $\dfrac{5}{3}$s là
[A]. 4cm
[B]. 24 cm
[C]. 14,9 cm
[D]. 12 cm
∆t =$\dfrac{5}{3}s=\dfrac{5T}{6}=\dfrac{T}{2}+\dfrac{T}{3}$ → \[{{S}_{\max }}=2A+A\sqrt{3}=14,9\]cm.
Câu 17.
Một vật dao động điều hòa với chu kỳ 7 s, biên độ 7 cm. Trong khoảng thời gian 2017 s, quãng đường lớn nhất mà vật có thể đi được là
[A]. 40,35m.
[B]. 80,7 m
[C]. 80,6 m.
[D]. 40,30 cm.
T = 7 s → ∆t =$2017s=576.\dfrac{T}{2}+\dfrac{T}{7}$ → \[{{S}_{\max \left( 2017s \right)}}=576.2A+2A\sin \dfrac{\pi }{7}=80,7\]m
Câu 18.
Một vật dao động điều hòa với chu kỳ 2 s, biên độ 10 cm. Quãng đường vật có thể đi được trong khoảng thời gian $\dfrac{5}{6}s$ là
[A]. 10 cm
[B]. 15 cm
[C]. 20 cm
[D]. 25 cm
T = 2 s → ∆t =$\dfrac{5}{6}s=\dfrac{5T}{12}<\dfrac{T}{2}$
→ \[{{S}_{\max }}=2A\sin \dfrac{5.\pi }{12}=19,3\]cm; \[{{S}_{\min }}=2A\left( 1-\cos \dfrac{5.\pi }{12} \right)=14,8\]cm
Quãng đường vật S có thể đi được phải thỏa mãn Smin < S < Smax .
Câu 19.
Một vật dao động điều hòa với chu kỳ 1s, biên độ 10 cm. Quãng đường vật có thể đi được trong khoảng thời gian 0,25s là
[A]. 4cm.
[B]. 5 cm
[C]. 10 cm
[D]. 15 cm
∆t =$0,25\text{s}=\dfrac{T}{4}$ → \[{{S}_{\max }}=2A\sin \dfrac{\pi }{4}=14,14\]cm; \[{{S}_{\min }}=2A\left( 1-\cos \dfrac{\pi }{4} \right)=5,86\]cm
Quãng đường vật S có thể đi được phải thỏa mãn Smin < S < Smax
Câu 20.
Một vật dao động điều hòa với chu kỳ 2 s, biên độ 8 cm. Quãng đường vật có thể đi được trong khoảng thời gian 1,8 s là
[A]. 27 cm
[B]. 30 cm
[C]. 33 cm
[D]. 24 cm
∆t =$\text{1}\text{,8s}=\dfrac{T}{2}+\dfrac{2T}{5}$ → \[{{S}_{\max }}=2\text{A}+2A\sin \dfrac{2\pi }{5}=31,2\]cm; \[{{S}_{\min }}=2\text{A}+2A\left( 1-\cos \dfrac{2\pi }{5} \right)=27,1\]cm
Quãng đường vật S có thể đi được phải thỏa mãn Smin < S < Smax .
Câu 21.
Một vật dao động điều hòa với phương trình $x=4\cos \left( \dfrac{4\pi t}{3}+\dfrac{\pi }{3} \right)cm$ trên trục Ox. Trong 1,75 s thì quãng đường đi được của vật không thể bằng
[A]. 18 cm
[B]. 17 cm
[C]. 19 cm
[D]. 20 cm
T = 1,5 s → ∆t =$\text{1}\text{,75s}=2.\dfrac{T}{2}+\dfrac{T}{6}$
→ \[{{S}_{\max }}=4\text{A}+2A\sin \dfrac{\pi }{6}=20\]cm; \[{{S}_{\min }}=4\text{A}+2A\left( 1-\cos \dfrac{\pi }{6} \right)=17,07\]cm
Quãng đường vật S có thể đi được phải thỏa mãn Smin < S < Smax .
→ Trong 1,75 s thì quãng đường đi được của vật không thể bằng 17 cm
Câu 22.
Một con lắc dao động điều hòa theo phương ngang với biên độ A, chu kì 3 s. Trong quá trình dao động, tốc độ trung bình lớn nhất của vật trong thời gian 0,5 s bằng 16 cm/s. Giá trị của A bằng
[A]. 2 cm
[B]. 4 cm
[C]. 16 cm
[D]. 8 cm
T = 3 s → ∆t =$\text{0}\text{,5s}=\dfrac{T}{6}$
→ \[{{v}_{tb(0,5\text{s})\max }}=\dfrac{{{S}_{\max \left( 0,5s \right)}}}{0,5s}=\dfrac{A}{0,5s}=16\]cm → A = 8 cm.
Câu 23.
Một con lắc dao động điều hòa theo phương ngang với biên độ 6 cm, chu kì 2 s. Trong quá trình dao động, tốc độ trung bình nhỏ nhất của vật trong thời gian 3,6 s liên tục bằng
[A]. 10,121 cm/s.
[B]. 11,374 cm/s.
[C]. 10,536 cm/s.
[D]. 10,972 cm/s.
∆t =$\text{3}\text{,6s}=3\dfrac{T}{2}+\dfrac{3T}{10}$
→ \[{{v}_{tb(3,6\text{s})min}}=\dfrac{{{S}_{\min \left( 3,6s \right)}}}{3,6s}=\dfrac{6A+2A\left( 1-\cos \dfrac{3\pi }{10} \right)}{3,6s}=11,374\]cm.
Câu 24.
Một con lắc dao động điều hòa theo phương ngang với biên độ A, chu kì 1,2 s. Trong quá trình dao động, tốc độ trung bình lớn nhất của vật trong thời gian 3,2 s liên tục bằng 23,375 cm/s. Giá trị A là
[A]. 6,8 cm/s.
[B]. 4,3 cm
[C]. 3,2 cm.
[D]. 8,6 cm.
∆t =$\text{3}\text{,2s}=5\dfrac{T}{2}+\dfrac{T}{6}$
→ \[{{v}_{tb(3,2\text{s})max}}=\dfrac{{{S}_{\max \left( 3,2s \right)}}}{3,2s}=\dfrac{10A+2A\sin \dfrac{\pi }{6}}{3,2s}=23,375\]cm → A = 6,8 cm.
Câu 25.
Một chất điểm dao động điều hòa với phương trình x = Acos2πt, t đo bằng s. Biết hiệu quãng đường lớn nhất và nhỏ nhất mà chất điểm đi được cùng trong một khoảng thời gian Δt đạt cực đại. Khoảng thời gian Δt có thể bằng
[A]. 1/6 (s).
[B]. 1/2 (s).
[C]. 1/4 (s).
[D]. 1/12 (s).
${{S}_{m\text{ax}}}-{{S}_{\min }}\le \left( 2\sqrt{2}-2 \right)A$, hiệu ${{S}_{m\text{ax}}}-{{S}_{\min }}$đạt giá trị lớn nhất khi $\Delta {t}’=\dfrac{T}{4}\Rightarrow \Delta t=n\dfrac{T}{2}+\dfrac{T}{4}$.
Ta có T = 1 s → $\Delta t$ = $\dfrac{1}{4}s;\text{ }\dfrac{3}{4}s;\text{ }\dfrac{5}{4}s;\text{ }\dfrac{7}{4}s;…$
Câu 26.
Một vật dao động điều hòa trên trục Ox có chu kỳ T = 0,6 s. Sau 0,1 s kể từ thời điểm ban đầu quãng đường vật đi được là 5 cm và đang đi theo chiều dương trục Ox. Trong quá trình vật dao động, quãng đường nhỏ nhất vật đi được trong khoảng thời gian 1,7 s là 55 cm. Phương trình dao động của vật là
[A]. $x=5\cos \left( \dfrac{10\pi }{3}t+\dfrac{2\pi }{3} \right)$cm
[B]. $x=5\cos \left( \dfrac{10\pi }{3}t+\dfrac{\pi }{3} \right)$cm
[C]. $x=5\cos \left( \dfrac{10\pi }{3}t-\dfrac{2\pi }{3} \right)$ cm
[D]. $x=10\cos \left( \dfrac{10\pi }{3}t-\dfrac{\pi }{3} \right)$cm
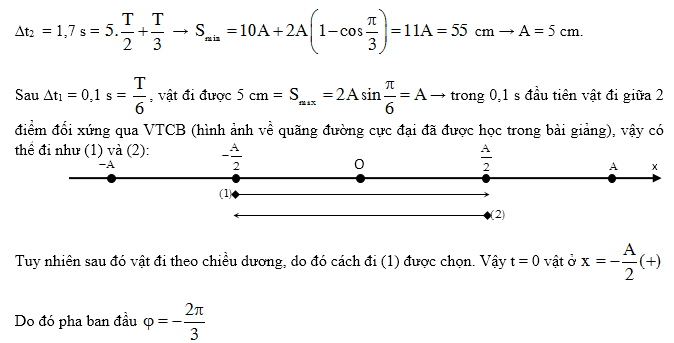
Câu 27.
Một vật dao động điều hòa trên trục Ox có chu kỳ T = 1 s. Sau $\dfrac{1}{3}$s kể từ thời điểm ban đầu quãng đường vật đi được là 4 cm và đang đi theo chiều dương trục Ox. Trong quá trình vật dao động, quãng đường lớn nhất vật đi được trong khoảng thời gian 3,25 s là 53,6568 cm. Lấy $\sqrt{2}=1,4142$. Phương trình dao động của vật là
[A]. $x=8\cos \left( 2\pi t+\dfrac{\pi }{3} \right)$cm
[B]. $x=4\cos \left( 2\pi t+\dfrac{\pi }{3} \right)$cm
[C]. $x=4\cos \left( 2\pi t+\dfrac{2\pi }{3} \right)$ cm
[D]. $x=4\cos \left( 2\pi t-\dfrac{\pi }{3} \right)$cm
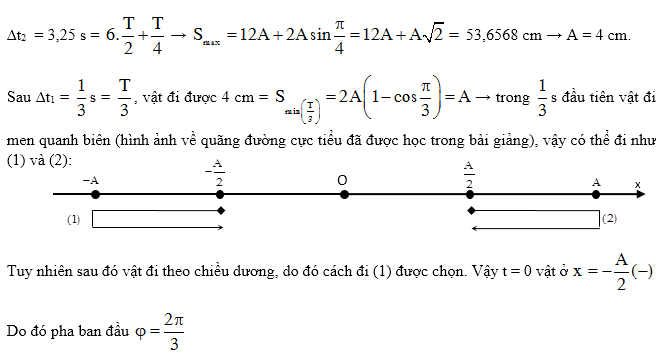
Câu 28.
Một vật dao động điều hoà với biên độ A, tần số f. Thời gian ngắn nhất để vật đi được quãng đường có độ dài A là:
[A]. \[\dfrac{1}{4f}.\]
[B]. \[\dfrac{1}{6f}.\]
[C]. \[\dfrac{1}{12f}.\]
[D]. \[\dfrac{1}{3f}\]
$A = 2A\sin \dfrac{{\pi \Delta {t_{\min }}}}{T} \to \Delta {t_{\min }} = \dfrac{T}{6} = \dfrac{1}{{6f}}$
Câu 29.
Một vật dao động điều hòa với biên độ A và tần số T. Khoảng thời gian lớn nhất để vật đi được quãng đường có độ dài A là
[A]. \[\dfrac{T}{6}.\]
[B]. \[\dfrac{T}{4}.\]
[C]. \[\dfrac{T}{3}.\]
[D]. \[\dfrac{T}{12}.\]
$A = 2A\left( {1 – \cos \dfrac{{\pi \Delta {t_{\max }}}}{T}} \right) \to \Delta {t_{\max }} = \dfrac{T}{3}$
Câu 30.
Một vật dao động điều hoà với biên độ A, chu kì T. Thời gian cần thiết để vật đi hết quãng đường A nằm trong khoảng từ ∆$t_{min}$ đến ∆$t_{max}$. Hiệu số ∆$t_{max}$ – ∆$t_{min}$ bằng
[A]. \[\dfrac{T}{4}.\]
[B]. \[\dfrac{T}{6}.\]
[C]. \[\dfrac{T}{12}.\]
[D]. \[\dfrac{T}{3}\]
$A=2A\sin \dfrac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min }}=\dfrac{T}{6}=\dfrac{1}{6f}$
$A=2A\left( 1-\cos \dfrac{\pi \Delta {{t}_{\max }}}{T} \right)\to \Delta {{t}_{\max }}=\dfrac{T}{3}$
→ ∆tmax – ∆tmin = $\dfrac{T}{6}$.
Câu 31.
Một vật dao động điều hòa với biên độ A và tần số f. Khoảng thời gian ngắn nhất để vật đi được quãng đường có độ dài \[A\sqrt{2}\] là
[A]. \[\dfrac{1}{6f}.\]
[B]. \[\dfrac{1}{4f}.\]
[C]. \[\dfrac{1}{3f}.\]
[D]. \[\dfrac{1}{12f}.\]
$A\sqrt 2 = 2A\sin \dfrac{{\pi \Delta {t_{\min }}}}{T} \to \Delta {t_{\min }} = \dfrac{T}{4}$
Câu 32.
Một vật dao động điều hòa với biên độ bằng 4 cm, chu kì 2 s. Khoảng thời gian nhỏ nhất vật cần để đi được quãng đường \[4\sqrt{3}\] cm là
[A]. \[\dfrac{1}{3}\text{ }s.\]
[B]. \[\dfrac{1}{6}\text{ }s.\]
[C]. \[\dfrac{2}{3}\text{ }s.\]
[D]. \[\dfrac{3}{4}\text{ }s.\]
$S = 4\sqrt 3 < 2{\rm{A}} = 8 \to 4\sqrt 3 = 2A\sin \dfrac{{\pi \Delta {t_{\min }}}}{T} = 2.4.\sin \dfrac{{\pi \Delta {t_{\min }}}}{T} \to \Delta {t_{\min }} = \dfrac{T}{3} = \dfrac{2}{3}\left( s \right)$
Câu 33.
Một vật dao động điều hòa với biên độ bằng 4 cm. Khoảng thời gian lớn nhất vật cần để đi được quãng đường 7 cm là 2 s. Chu kì dao động của vật là
[A]. 4,35 s
[B]. 3,54 s
[C]. 0,92 s
[D]. 2,54 s
$S = 7 < 2{\rm{A}} = 8 \to 7 = 2A\left( {1 – \cos \dfrac{{\pi \Delta {t_{\max }}}}{T}} \right) \to \Delta {t_{\max }} = 0,46T = 2 \to T = 4,35{\rm{ }}s$
Câu 34.
Một vật dao động điều hòa với biên độ bằng 6 cm và chu kì 6 s. Khoảng thời gian nhỏ nhất vật cần để đi được quãng đường 66 cm là
[A]. 12,34 s
[B]. 13,78 s
[C]. 16 s
[D]. 17,64 s
$S=66=5.2A+A$
Để đi 10A luôn cần $5.\dfrac{T}{2}$ , thời gian ngắn nhất để đi A là:
$A=2A\sin \dfrac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min }}=\dfrac{T}{6}$
Vậy thời gian ngắn nhất để đi 66 cm là: $5.\dfrac{T}{2}+\dfrac{T}{6}$ = 16 s .
Câu 35.
Một vật thực hiện dao động điều hòa với biên độ 4 cm. Trong khoảng thời gian ∆t quãng đường dài nhất mà vật đi được là 20 cm. Quãng đường ngắn nhất vật đi được trong khoảng thời gian trên bằng
[A]. 17,07 cm
[B]. 13,07 cm
[C]. 15,87 cm
[D]. 12,46 cm
$S=20=2.2A+A$
Để đi 4A luôn cần $2.\dfrac{T}{2}$ , thời gian ngắn nhất để đi A là:
$A=2A\sin \dfrac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min }}=\dfrac{T}{6}$
Vậy thời gian ngắn nhất ∆t để đi 20 cm là: $\Delta t=2.\dfrac{T}{2}+\dfrac{T}{6}$
Quãng đường ngắn nhất vật đi trong ∆t là:
${{S}_{\min }}=4A+2A\left( 1-\cos \dfrac{\pi }{6} \right)$ = 17,07 cm
Câu 36.
Một vật dao động điều hòa với biên độ bằng 9 cm và chu kì 6 s. Khoảng thời gian lớn nhất vật cần để đi được quãng đường 96 cm là
[A]. 15,34 s
[B]. 16,61 s
[C]. 18.56 s
[D]. 17,64 s
$S=96=5.2A+\dfrac{2A}{3}$
Để đi 10A luôn cần $5.\dfrac{T}{2}$ , thời gian lớn nhất để đi $\dfrac{2\text{A}}{3}$ là: $\dfrac{2\text{A}}{3}=2A\left( 1-\cos \dfrac{\pi \Delta {{t}_{\min }}}{T} \right)\to \Delta {{t}_{\min }}=0,268T$
Vậy thời gian lớn nhất để đi 96 cm là: $\Delta t=5.\dfrac{T}{2}+0,268T=16,608\text{ }s.$
Câu 37.
Một vật dao động điều hòa với biên độ bằng 4 cm. Khoảng thời gian nhỏ nhất vật cần để đi được quãng đường 12 cm là 0,8 s. Số dao động toàn phần mà vật thực hiện trong khoảng thời gian mỗi phút là
[A]. 45
[B]. 43
[C]. 34
[D]. 50
$S=12=2A+A$
Để đi 2A luôn cần $\dfrac{T}{2}$ , thời gian nhỏ nhất để đi A là:
$A=2A\sin \dfrac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min }}=\dfrac{T}{6}$
Vậy thời gian ngắn nhất để đi 12 cm là:
$\Delta t=\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2T}{3}=0,8\text{ s}\to \text{T = 1}\text{,2 s}\text{.}$
Trong một phút số dao động toàn phần vật thực hiện là: $\dfrac{60}{T}=50$.
Câu 38.
Một vật thực hiện dao động điều hòa với biên độ 4 cm. Tốc độ trung bình lớn nhất mà vật chuyển động trên quãng đường $4\sqrt{3}$cm là $0,3\sqrt{3}$m/s. Chu kì dao động của vật là
[A]. 0,1 s
[B]. 0,4 s
[C]. 0,3 s
[D]. 0,2 s
Quãng đường phải đi không đổi, để tốc độ trung bình lớn nhất thì thời gian dao động phải nhỏ nhất, do đó:
∆tmin = $\dfrac{S}{{{v}_{tb-\max }}}=\dfrac{2}{15}s$
Quãng đường $4\sqrt{3}$ < 2A → $4\sqrt{3}=2A\sin \dfrac{\pi \Delta {{t}_{\min }}}{T}\to \Delta {{t}_{\min }}=\dfrac{T}{3}=\dfrac{2}{15}\to T=0,4\text{ s}\text{.}$
Câu 39.
Một vật dao động điều hoà với chu kỳ T và biên độ A, tốc độ trung bình bé nhất của vật khi thực hiện được quãng đường 5A là
[A]. $\dfrac{{6A(2 – \sqrt 3 )}}{T}$
[B]. $\dfrac{{5A}}{{2T}}$
[C]. $\dfrac{{15A}}{{4T}}$
[D]. $\dfrac{{5A}}{T}$
Muốn tốc độ trung bình bé nhất thì 5A phải thực hiện trong khoảng thời gian lớn nhất.
5A = 2.2A + A → 4A luôn mất T, A thực hiện trong khoảng thời gian dài nhất là:
$A=2A\left( 1-\cos \dfrac{\pi \Delta {{t}_{\max }}}{T} \right)\to \Delta {{t}_{\max }}=\dfrac{T}{3}$
Vậy khoảng thời gian lớn nhất để vật đi được quãng đường 5A là:
\[T+\dfrac{T}{3}=\dfrac{4T}{3}\]
Tốc độ trung bình bé nhất cần tìm: ${{v}_{tb-\min }}=\dfrac{5A}{\dfrac{4T}{3}}=\dfrac{15A}{4T}$