Mạch RLC nối tiếp R thay đổi để có cùng công suất hoặc cùng cường độ dòng điện
Câu 1.
Đoạn mạch xoay chiều gồm cuộn dây thuần cảm L nối tiếp với biến trở R. Đặt vào hai đầu mạch điện áp xoay chiều \[u={{U}_{0}}cos\left( 2\pi ft \right). \] Khi biến trở nhận các giá trị \[{{R}_{1}}\] và \[{{R}_{2}}\] thì điện áp hai đầu mạch lệch pha \[{{\varphi }_{1}}\] và \[{{\varphi }_{2}}\] so với cường độ dòng điện qua mạch. Biết \[{{\varphi }_{1}}+{{\varphi }_{2}}=\] $\dfrac{\pi }{2}$. Giá trị độ tự cảm của cuộn dây là:
[A]. L = \[\dfrac{{{R}_{1}}+{{R}_{2}}}{2\pi f}\].
[B]. L = \[\dfrac{{{R}_{1}}{{R}_{2}}}{2\pi f}\].
[C]. L = \[\dfrac{\sqrt{{{R}_{1}}{{R}_{2}}}}{2\pi f}\].
[D]. L = \[\dfrac{\left| {{R}_{1}}-{{R}_{2}} \right|}{2\pi f}\].
Ta có : ${{\varphi }_{1}}+{{\varphi }_{2}}=\dfrac{\pi }{2}\to \tan {{\varphi }_{1}}. \tan {{\varphi }_{2}}=1\to \dfrac{{{Z}_{L}}}{{{R}_{1}}}. \dfrac{{{Z}_{L}}}{{{R}_{2}}}=1\to Z_{L}^{2}={{R}_{1}}. {{R}_{2}}\Rightarrow L=\sqrt{\dfrac{{{R}_{1}}. {{R}_{2}}}{2\pi f}}$
Câu 2.
Cho đoạn mạch điện xoay chiều gồm cuộn tụ điện có điện dung C nối tiếp với biến trở R. Điện áp hai đầu đoạn mạch là U ổn định, có tần số f. Ta thấy có hai giá trị của biến trở R là \[{{R}_{1}}\] và \[{{R}_{2}}\] làm công suất tỏa nhiệt trên biến trở không đổi. Giá trị của điện dung C là
[A]. $C=\dfrac{1}{2\pi f{{R}_{1}}{{R}_{2}}}. $
[B]. $C=\dfrac{2\pi f}{\sqrt{{{R}_{1}}{{R}_{2}}}}. $
[C]. $C=\dfrac{\sqrt{{{R}_{1}}{{R}_{2}}}}{2\pi f}. $
[D]. $C=\dfrac{1}{2\pi f\sqrt{{{R}_{1}}{{R}_{2}}}}. $
Có hai giá trị của biến trở R là \[{{R}_{1}}\] và \[{{R}_{2}}\] làm công suất tỏa nhiệt trên biến trở không đổi: $\to {{R}_{1}}{{R}_{2}}={{Z}_{C}}^{2}\to C=\dfrac{1}{2\pi f\sqrt{{{R}_{1}}{{R}_{2}}}}$
Câu 3.
Cho mạch điện xoay chiều gồm biến trở R và tụ \[C={{10}^{-4}}/\pi \left( F \right)\] mắc nối tiếp. Đặt vào hai đầu mạch điện một hiệu điện thế xoay chiều ổn định tần số 50 Hz. Thay đổi R ta thấy ứng với hai giá trị \[R={{R}_{1}}\] và \[R={{R}_{2}}\] thì công suất của mạch điện đều bằng nhau. Khi đó tích số \[{{R}_{1}}{{R}_{2}}\] là:
[A]. \[{{2. 10}^{4}}\left( {{\Omega }^{2}} \right)\]
[B]. \[{{10}^{2}}\left( {{\Omega }^{2}} \right)\]
[C]. \[{{2. 10}^{2}}\left( {{\Omega }^{2}} \right)\]
[D]. \[{{10}^{4}}\left( {{\Omega }^{2}} \right)\]
Với hai giá trị \[R={{R}_{1}}\] và \[R={{R}_{2}}\] thì công suất của mạch điện đều bằng nhau: $\to {{R}_{1}}{{R}_{2}}={{Z}_{C}}^{2}={{10}^{4}}({{\Omega }^{2}})$
Câu 4.
Cho một đoạn mạch nối tiếp gồm một cuộn dây thuần cảm L, một tụ điện C và một biến trở R. Điện áp giữa hai đầu đoạn mạch bằng U không đổi. Khi điện trở của biến trở bằng \[{{R}_{1}}\] và \[{{R}_{2}}\] ng¬¬ười ta thấy công suất tiêu thụ trong đoạn mạch trong hai trư¬¬ờng hợp bằng nhau. Tìm công suất cực đại khi điện trở của biến trở thay đổi?
[A]. $\dfrac{{{U}^{2}}}{2\sqrt{{{R}_{1}}{{R}_{2}}}}. $
[B]. $\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}. $
[C]. $\dfrac{2{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}. $
[D]. $\dfrac{2{{U}^{2}}\left( {{R}_{1}}+{{R}_{2}} \right)}{4{{R}_{1}}{{R}_{2}}}. $
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì \[\left\{ \begin{align} & P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}} \\ & {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}_{1}}{{R}_{2}} \\ \end{align} \right. \] $\xrightarrow{{}}$ Để công suất mạch cực đại thì \[{{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|\]; \[{{P}_{m\text{ax}}}=\dfrac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\dfrac{{{U}^{2}}}{2{{R}_{0}}}=\dfrac{{{U}^{2}}}{2\sqrt{{{R}_{1}}{{R}_{2}}}}\]
Câu 5.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch RLC nối tiếp có R thay đổi thì thấy khi \[{{R}_{1}}=30\Omega \] và \[{{R}_{2}}=120\Omega \] thì công suất toả nhiệt trên đoạn mạch không đổi. Để công suất đó đạt cực đại thì giá trị R là
[A]. 24 Ω.
[B]. 90 Ω
[C]. 150 Ω.
[D]. 60 Ω.
Để công suất đó đạt cực đại thì giá trị R là: ${{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}=60\Omega $
Câu 6.
Cho đoạn mạch RLC nối tiếp, R thay đổi được, điện áp hai đầu đoạn mạch \[u=60\sqrt{2}\sin \left( 100\pi t \right)V. \] Khi \[R={{R}_{1}}=9\Omega \] hoặc \[R={{R}_{2}}=16\Omega \] thì công suất trong mạch như nhau. Hỏi với giá trị nào của R thì công suất mạch cực đại, giá trị cực đại đó?
[A]. \[12\Omega ;150W\] .
[B]. \[12\Omega ;100W. \]
[C]. \[10\Omega ;150W\] .
[D]. \[10\Omega ;100W\] .
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì \[\left\{ \begin{align} & P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}} \\ & {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}_{1}}{{R}_{2}} \\ \end{align} \right. \] $\xrightarrow{{}}$ Để công suất mạch cực đại thì \[{{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|=\sqrt{9. 16}=12\Omega \]; \[{{P}_{m\text{ax}}}=\dfrac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\dfrac{{{U}^{2}}}{2{{R}_{0}}}=\dfrac{{{U}^{2}}}{2\sqrt{{{R}_{1}}{{R}_{2}}}}=150\text{W}. \]
Câu 7.
Đặt một điện áp xoay chiều có giá trị hiệu dụng U = 100 V vào hai đầu đoạn mạch RLC nối tiếp, cuộn dây thuần cảm kháng, R có giá trị thay đổi được. Điều chỉnh R ở hai giá trị \[{{R}_{1}}\] và \[{{R}_{2}}\] sao cho \[{{R}_{1}}+{{R}_{2}}=100\Omega \] thì thấy công suất tiêu thụ của đoạn mạch ứng với hai trường hợp này như nhau. Công suất này có giá trị là
[A]. 50 W.
[B]. 100 W.
[C]. 400 W.
[D]. 200 W.
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì: \[P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}=100W. \]
Câu 8.
Đoạn mạch gồm biến trở R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp, được mắc vào điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Khi điều chỉnh biến trở đến các giá trị \[16\Omega \] và \[64\Omega \] thì công suất của mạch bằng nhau và bằng 80W. Điện áp hiệu dụng hai đầu đoạn mạch bằng
[A]. U = 64V.
[B]. U = 80V.
[C]. U = 16V.
[D]. U = 32V.
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì: \[P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}\to U=80V. \]
Câu 9. CĐ2010
Đặt điện áp u = $U\sqrt{2}\cos \omega t$ (V) vào hai đầu đoạn mạch gồm cuộn cảm thuần mắc nối tiếp với một biến trở R. Ứng với hai giá trị \[{{R}_{1}}=20\Omega \] và \[{{R}_{2}}=80\Omega \] của biến trở thì công suất tiêu thụ trong đoạn mạch đều bằng 400 W. Giá trị của U là
[A]. 400 V.
[B]. 200 V.
[C]. 100 V.
[D]. $100\sqrt{2}$V.
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì: \[P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}\to U=200V. \]
Câu 10.
Đoạn mạch gồm biến trở R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp, được mắc vào điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Khi điều chỉnh biến trở đến các giá trị 16Ω và 64Ω thì công suất của mạch bằng nhau và bằng 180W. Điện áp hiệu dụng hai đầu đoạn mạch bằng
[A]. U = 64V.
[B]. U = 120V.
[C]. U = 16V.
[D]. U = 32V.
+ Với \[R={{R}_{1}}\] ; \[R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì: \[P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}\to U=120V. \]
Câu 11.
Đặt điện áp $\text{u = U}\sqrt{\text{2}}\text{cos}\omega \text{t (V)}$vào hai đầu một đoạn mạch gồm biến trở R và tụ điện có điện dung C mắc nối tiếp. Khi $\text{R = }{{\text{R}}_{\text{1}}}\text{ ; R = }{{\text{R}}_{\text{2}}}$ thì công suất tiêu thụ trên đoạn mạch là như nhau và ${{\text{R}}_{\text{2}}}\text{= 8}{{\text{R}}_{\text{1}}}$. Hệ số công suất của đoạn mạch ứng với các giá trị ${{\text{R}}_{\text{1}}}$ và ${{\text{R}}_{\text{2}}}$lần lượt là
[A]. $\dfrac{\text{1}}{\text{3}};\dfrac{\text{2}\sqrt{\text{2}}}{\text{3}}$.
[B]. $\text{ }\dfrac{\text{2}\sqrt{\text{2}}}{\text{3}}\text{ ;}\dfrac{\text{1}}{\text{3}}$.
[C]. $\dfrac{\sqrt{\text{3}}}{\text{2}}\text{;}\dfrac{\text{1}}{\text{2}}$.
[D]. $\dfrac{\text{1}}{\text{2}}\text{;}\dfrac{\sqrt{\text{3}}}{\text{2}}$.
Với hai giá trị \[R={{R}_{1}}\] và \[R={{R}_{2}}\] thì công suất của mạch điện đều bằng nhau: $\to {{R}_{1}}{{R}_{2}}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}$ Hệ số công suất của đoạn mạch ứng với các giá trị ${{\text{R}}_{\text{1}}}$ và ${{\text{R}}_{\text{2}}}$lần lượt là $\cos {{\varphi }_{1}}=\dfrac{{{R}_{1}}}{{{Z}_{1}}}=\dfrac{{{R}_{1}}}{\sqrt{R_{1}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{{{R}_{1}}}{\sqrt{R_{1}^{2}+{{R}_{1}}{{R}_{2}}}}=\dfrac{{{R}_{1}}}{\sqrt{R_{1}^{2}+{{R}_{1}}. 8{{R}_{1}}}}=\dfrac{1}{3}$ $\cos {{\varphi }_{2}}=\dfrac{{{R}_{2}}}{{{Z}_{2}}}=\dfrac{{{R}_{2}}}{\sqrt{R_{2}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{{{R}_{2}}}{\sqrt{R_{2}^{2}+{{R}_{1}}{{R}_{2}}}}=\dfrac{{{R}_{2}}}{\sqrt{R_{2}^{2}+\dfrac{1}{8}{{R}_{2}}. {{R}_{2}}}}=\dfrac{2\sqrt{2}}{3}$
Câu 12. ĐH2009
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch gồm biến trở R mắc nối tiếp với tụ điện. Dung kháng của tụ điện là \[100\Omega \]. Khi điều chỉnh R thì tại hai giá trị \[{{R}_{1}}\] và \[{{R}_{2}}\] công suất tiêu thụ của đoạn mạch như nhau. Biết điện áp hiệu dụng giữa hai đầu tụ điện khi \[R={{R}_{1}}\] bằng hai lần điện áp hiệu dụng giữa hai đầu tụ điện khi \[R={{R}_{2}}\]. Các giá trị \[{{R}_{1}}\] và \[{{R}_{2}}\] là
[A]. \[{{R}_{1}}=50\Omega ,{{R}_{2}}=100\Omega . \]
[B]. \[{{R}_{1}}=40\Omega ,{{R}_{2}}=250\Omega . \]
[C]. \[{{R}_{1}}=50\Omega ,{{R}_{2}}=200\Omega . \]
[D]. \[{{R}_{1}}=25\Omega ,{{R}_{2}}=100\Omega . \]
Với hai giá trị \[R={{R}_{1}}\] và \[R={{R}_{2}}\] thì công suất của mạch điện đều bằng nhau: $\to {{R}_{1}}{{R}_{2}}=Z_{C}^{2}={{10}^{4}}({{\Omega }^{2}})$ Theo bài cho ta có: ${{U}_{C1}}=2{{U}_{C2}}\to {{I}_{1}}=2{{I}_{2}}\to {{Z}_{2}}=2{{Z}_{1}}\to R_{2}^{2}+Z_{C}^{2}=4\left( R_{1}^{2}+Z_{C}^{2} \right)$ $R_{2}^{2}+{{10}^{4}}=4\left( R_{1}^{2}+{{10}^{4}} \right)\to \dfrac{{{10}^{8}}}{R_{1}^{2}}+{{10}^{4}}=4\left( R_{1}^{2}+{{10}^{4}} \right)\to {{R}_{1}}=50\Omega \to {{R}_{2}}=200\Omega $
Câu 13.
Đặt điện áp \[u=120\sqrt{2}\cos 100\pi t\,(V)\] vào hai đầu đoạn mạch nối tiếp gồm biến trở R, tụ điện $C=\dfrac{1}{4\pi }\,mF$ và cuộn cảm thuần $L=\dfrac{1}{\pi }\,(H). $ Khi thay đổi giá trị của biến trở thì ứng với hai giá trị của biến trở là ${{R}_{1}}$ và ${{R}_{2}}$ thì mạch tiêu thụ cùng một công suất P và độ lệch pha của điện áp hai đầu đoạn mạch so với dòng điện trong mạch tương ứng là ${{\varphi }_{1}},\,\,\,{{\varphi }_{2}}$ với ${{\varphi }_{1}}=2{{\varphi }_{2}}. $ Giá trị công suất P bằng
[A]. $120\,\,\text{W}\text{. }$
[B]. $240\,\,\text{W}\text{. }$
[C]. $60\sqrt{3}\,\,\text{W}\text{. }$
[D]. $120\sqrt{3}\,\,\text{W}\text{. }$
Khi thay đổi giá trị của biến trở thì ứng với hai giá trị của biến trở là ${{R}_{1}}$ và ${{R}_{2}}$ thì mạch tiêu thụ cùng một công suất : ${{R}_{1}}{{R}_{2}}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{(100-40)}^{2}}=3600({{\Omega }^{2}})$ Và $\left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\dfrac{\pi }{2}\to {{\varphi }_{1}}+{{\varphi }_{2}}=\dfrac{\pi }{2}(1)$ Bài cho: ${{\varphi }_{1}}=2{{\varphi }_{2}}(2)$ Từ (1) và (2) suy ra: ${{\varphi }_{2}}=\dfrac{\pi }{6}rad\Rightarrow \tan {{\varphi }_{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{{{R}_{2}}}$ $\to {{R}_{2}}=\sqrt{3}({{Z}_{L}}-{{Z}_{C}})=60\sqrt{3}\Omega \to {{R}_{1}}=20\sqrt{3}\Omega . $ Giá trị công suất P bằng: \[P=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}=60\sqrt{3}\text{W}. \]
Câu 14.
Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu một đoạn mạch RLC nối tiếp, điện trở R có thể thay đổi được. Khi R thì thấy với hai giá trị của điện trở R là \[45\Omega \] và \[80\Omega \] thì công suất tiêu thụ trên đoạn mạch là như nhau. Hệ số công suất của mạch khi \[R=45\Omega \] là
[A]. 0,6.
[B]. 0,7.
[C]. 0,8.
[D]. 0,75.
$\left\{ \begin{align} & {{R}_{1}}=45\Omega \\ & {{R}_{2}}=80\Omega \\ \end{align} \right. \Rightarrow {{P}_{1}}={{P}_{2}}\Leftrightarrow {{R}_{0}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|=\sqrt{{{R}_{1}}{{R}_{2}}}=60\Omega $ R = 45 Ω $\Rightarrow Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{{{45}^{2}}+{{60}^{2}}}=75\Omega $ \[\text{cos}\varphi \text{=}\dfrac{R}{Z}=\dfrac{45}{75}=\dfrac{3}{5}\]
Câu 15.
Điện áp hai đầu mạch RLC mắc nối tiếp (có R là biến trở) là $u=120\sqrt{2}\cos 120\pi t$ (V). Khi \[R={{R}_{1}}=18\Omega \] và \[R={{R}_{2}}=32\Omega \] thì công suất mạch tiêu thụ là như nhau. Khi R thay đổi, công suất mạch tiêu thụ không thể nhận giá trị
[A]. 288 W.
[B]. 72 W.
[C]. 144 W.
[D]. 576 W.
+ Với \[R={{R}_{1}};R={{R}_{2}}\] công suất tiêu thụ của mạch cùng giá trị P thì để công suất tiêu thụ của mạch cực đại khi: $\xrightarrow{{}}$ \[{{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|\]; \[{{P}_{m\text{ax}}}=\dfrac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\dfrac{{{U}^{2}}}{2{{R}_{0}}}=\dfrac{{{U}^{2}}}{2\sqrt{{{R}_{1}}{{R}_{2}}}}=300W\] Như vậy công suất mạch tiêu thụ không thể nhận giá trị lớn hơn 300W.
Câu 16.
Một mạch RLC nối tiếp, trong đó cuộn dây thuần cảm, điện trở R thay đổi được. Khi cho \[R={{R}_{1}}\] hoặc \[R={{R}_{2}}\] thì công suất của mạch như nhau. Biết \[{{R}_{2}}=3{{R}_{1}}\]. Độ lớn của sự lệch pha giữa u và i khi \[R={{R}_{1}}\] là
[A]. $\dfrac{\pi }{3}$
[B]. $\dfrac{\pi }{6}$
[C]. $\dfrac{\pi }{4}$
[D]. $\dfrac{\pi }{12}$
${{P}_{1}}={{P}_{2}}\Leftrightarrow {{R}_{0}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|=\sqrt{{{R}_{1}}{{R}_{2}}}={{R}_{1}}\sqrt{3}$ \[\text{tan}{{\varphi }_{1}}\text{=}\dfrac{\left| {{Z}_{L}}-{{Z}_{C}} \right|}{{{R}_{1}}}=\sqrt{3}\Rightarrow {{\varphi }_{1}}\text{=}\dfrac{\pi }{3}\]
Câu 17.
Cho mạch điện xoay chiều RLC mắc nối tiếp, R là biến trở. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định $u=U\sqrt{2}\cos \omega t\left( V \right)$. Khi thay đổi giá trị của biến trở ta thấy có hai giá trị \[R={{R}_{1}}=45\Omega \] hoặc \[R={{R}_{2}}=80\Omega \] thì tiêu thụ cùng công suất P. Hệ số công suất của đoạn mạch điện ứng với hai trị của biến trở \[{{R}_{1}},{{R}_{2}}\] là
[A]. 0,5; 1.
[B]. 0,5; 0,8.
[C]. 0,8; 0,6.
[D]. 0,6; 0,8.
Với hai giá trị \[R={{R}_{1}}\] và \[R={{R}_{2}}\] thì công suất của mạch điện đều bằng nhau: $\to {{R}_{1}}{{R}_{2}}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}\to {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=3600$ Hệ số công suất của đoạn mạch ứng với các giá trị ${{\text{R}}_{\text{1}}}$ và ${{\text{R}}_{\text{2}}}$lần lượt là $\cos {{\varphi }_{1}}=\dfrac{{{R}_{1}}}{{{Z}_{1}}}=\dfrac{{{R}_{1}}}{\sqrt{R_{1}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{45}{\sqrt{{{45}^{2}}+3600}}=\dfrac{3}{5}=0,6. $ $\cos {{\varphi }_{2}}=\dfrac{{{R}_{2}}}{{{Z}_{2}}}=\dfrac{{{R}_{2}}}{\sqrt{R_{2}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{80}{\sqrt{{{80}^{2}}+3600}}=0,8. $
Câu 18.
Cho mạch điện có 2 phần tử mắc nối tiếp là tụ C và điện trở R. Độ lệch pha giữa \[{{u}_{AB}}\] và dòng điện i của mạch ứng với các giá trị \[{{R}_{1}}\] và \[{{R}_{2}}\] của R là \[{{\varphi }_{1}}\] và \[{{\varphi }_{2}}\]. Biết \[{{\varphi }_{1}}+{{\varphi }_{2}}=\]$\dfrac{\pi }{2}$. Cho\[{{R}_{1}}=270\Omega ,{{R}_{2}}=480\Omega ,{{U}_{AB}}=150V\]. Gọi \[{{P}_{1}}\] và \[{{P}_{2}}\] là công suất của mạch ứng với \[{{R}_{1}}\]và \[{{R}_{2}}\]. Giá trị \[{{P}_{1}}\] và \[{{P}_{2}}\] lần lượt là
[A]. \[{{P}_{1}}=40W;{{P}_{2}}=40W\] .
[B]. \[{{P}_{1}}=50W;{{P}_{2}}=40W\] .
[C]. \[{{P}_{1}}=40W;{{P}_{2}}=50W\] .
[D]. \[{{P}_{1}}=30W;{{P}_{2}}=30W\] .
Bài cho: ${{\varphi }_{1}}+{{\varphi }_{2}}=\dfrac{\pi }{2}\to \tan {{\varphi }_{1}}. \tan {{\varphi }_{2}}=1\Rightarrow \dfrac{-{{Z}_{C}}}{{{R}_{1}}}. \dfrac{-{{Z}_{C}}}{{{R}_{2}}}=1\to {{Z}_{C}}=\sqrt{{{R}_{1}}{{R}_{2}}}=360\Omega $ Công suất của mạch ứng với \[{{R}_{1}}\]và \[{{R}_{2}}\]lần lượt là : ${{P}_{1}}=I_{1}^{2}. {{R}_{1}}=\dfrac{{{U}^{2}}}{Z_{1}^{2}}. {{R}_{1}}=\dfrac{{{U}^{2}}}{R_{1}^{2}+Z_{C}^{2}}. {{R}_{1}}=30W$ ${{P}_{2}}=I_{2}^{2}. {{R}_{2}}=\dfrac{{{U}^{2}}}{Z_{2}^{2}}. {{R}_{2}}=\dfrac{{{U}^{2}}}{R_{2}^{2}+Z_{C}^{2}}. {{R}_{2}}=30W$
Câu 19.
Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu một đoạn mạch RLC nối tiếp, điện trở R có thể thay đổi được. Khi R thì thấy với hai giá trị của điện trở R là \[20\Omega \] và \[25\Omega \] thì công suất tiêu thụ trên đoạn mạch là như nhau. Hệ số công suất của mạch khi \[R=20\Omega \] là
[A]. 0,6.
[B]. $\dfrac{2}{3}$.
[C]. $\dfrac{\sqrt{3}}{2}$.
[D]. $\dfrac{3}{4}$.
Khi R thay đổi thấy có hai giá trị của điện trở R thì công suất tiêu thụ trên đoạn mạch là như nhau suy ra: ${{R}_{1}}{{R}_{2}}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=500$ Hệ số công suất của mạch khi \[R=20\Omega \] là: \[\cos \varphi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{2}{3}\]
Câu 20.
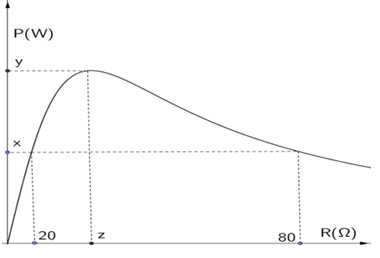
Đặt điện áp $u=200\sqrt{2}\cos (100\pi t+0,132)$ vào 2 đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ điện C người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình dưới. Giá trị x, y, z lần lượt là:
[A]. 400, 500, 40
[B]. 400, 400, 50
[C]. 500, 40, 50
[D]. 50, 400, 400
Khi \[\left\{ \begin{align} & {{R}_{1}}=20\Omega \\ & {{R}_{2}}=80\Omega \\ \end{align} \right. \Rightarrow {{P}_{1}}={{P}_{2}}=x=\dfrac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}=\dfrac{{{200}^{2}}}{20+80}=400W\] $|{{Z}_{L}}-{{Z}_{C}}|=\sqrt{{{R}_{1}}. {{R}_{2}}}=\sqrt{20. 80}=40\Omega $ ${{P}_{m\text{ax}}}=y=\dfrac{{{U}^{2}}}{2|{{Z}_{L}}-{{Z}_{C}}|}=\dfrac{{{200}^{2}}}{2. 40}=500W\Leftrightarrow R=z=|{{Z}_{L}}-{{Z}_{C}}|=40\Omega $
Câu 21.
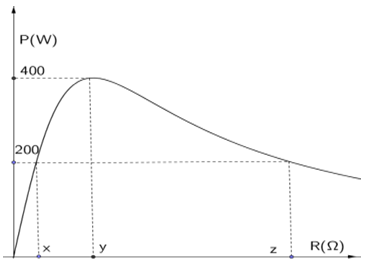
Đặt điện áp $u=200\sqrt{2}\cos (100\pi t-0,142)$vào 2 đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ điện C người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình dưới. Giá trị z gần nhất với:
[A]. 170
[B]. 180
[C]. 190
[D]. 200
${{P}_{m\text{ax}}}=\dfrac{{{U}^{2}}}{2|{{Z}_{L}}-{{Z}_{C}}|}\Leftrightarrow 400=\dfrac{{{200}^{2}}}{2. |{{Z}_{L}}-{{Z}_{C}}|}\Leftrightarrow y=|{{Z}_{L}}-{{Z}_{C}}|=50\Omega $ \[\left\{ \begin{align} & {{R}_{1}}=x \\ & {{R}_{2}}=z \\ \end{align} \right. \Rightarrow {{P}_{1}}={{P}_{2}}=200=\dfrac{{{U}^{2}}}{x+z}\Rightarrow x+z=200\Omega \left( 1 \right)\] $|{{Z}_{L}}-{{Z}_{C}}|=\sqrt{{{R}_{1}}. {{R}_{2}}}=\sqrt{x. z}=50\Omega \Rightarrow x. z=2500\left( 2 \right)$
Từ (1) và (2) ta có: \[\left\{ \begin{align}& x+z=200 \\ & x.z=2500 \\ \end{align} \right.\]
\[\Rightarrow \left\{ \begin{align}& x=13,4 \\ & y=186,6 \\ \end{align} \right.\]
Câu 22.
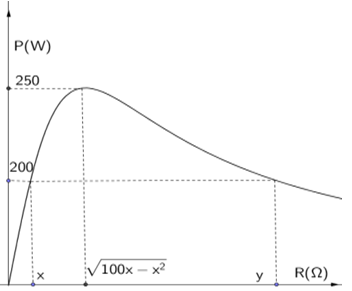
Đặt điện áp $u=U\sqrt{2}\cos (100\pi t)$vào 2 đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình dưới. Xác định y:
[A]. 20
[B]. 50
[C]. 80
[D]. 100
${{P}_{m\text{ax}}}=\dfrac{{{U}^{2}}}{2|{{Z}_{L}}-{{Z}_{C}}|}\Leftrightarrow 250=\dfrac{{{U}^{2}}}{2. |{{Z}_{L}}-{{Z}_{C}}|}\Leftrightarrow \sqrt{100x-{{x}^{2}}}=|{{Z}_{L}}-{{Z}_{C}}|=\dfrac{{{U}^{2}}}{500}(1)$
\[\left\{ \begin{align} & {{R}_{1}}=x \\ & {{R}_{2}}=y \\ \end{align} \right. \Rightarrow {{P}_{1}}={{P}_{2}}=200=\dfrac{{{U}^{2}}}{x+y}\Rightarrow x+y=\dfrac{{{U}^{2}}}{200}\left( 2 \right)\]
$|{{Z}_{L}}-{{Z}_{C}}|=\sqrt{{{R}_{1}}. {{R}_{2}}}=\sqrt{x. y}=\dfrac{{{U}^{2}}}{500}\left( 3 \right)$
Từ (1) và (3) ta có: $\sqrt{100x-{{x}^{2}}}=\sqrt{xy}\to x=100-y$
Từ (2) và (3) suy ra: $x+y=\dfrac{500\sqrt{xy}}{200}\to x+y=\dfrac{5\sqrt{xy}}{2}\Rightarrow {{(x+y)}^{2}}=\dfrac{25}{4}xy$ $\to {{(100-y+y)}^{2}}=\dfrac{25}{4}(100-y)y\Rightarrow y=80$
Câu 23.
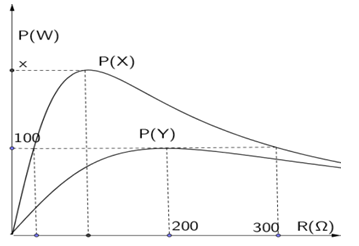
Đặt điện áp $u=U\sqrt{2}\cos (100\pi t+\varphi )$ lần lượt vào 2 đầu đoạn mạch gồm X và Y. Mỗi mạch đều chứa các phần tử: biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình dưới. Giá trị x là:
[A]. $\dfrac{200}{\sqrt{3}}$
[B]. $180\sqrt{3}$
[C]. $200\sqrt{3}$
[D]. $\dfrac{180}{\sqrt{3}}$
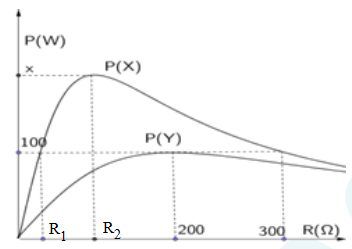
Từ đồ thị ta có: ${{P}_{Y\max }}=100=\dfrac{{{U}^{2}}}{2. 200}\to U=200V$
Khi ${{P}_{X}}=100W$ thì có hai giá trị của R thỏa mãn: $R={{R}_{1}};R=300\Omega $ suy ra: ${{P}_{x}}=100=\dfrac{{{U}^{2}}}{{{R}_{1}}+300}\to 100=\dfrac{{{200}^{2}}}{{{R}_{1}}+300}\to {{R}_{1}}=100\Omega $
Để ${{P}_{X\max }}$ thì ${{R}_{2}}=\sqrt{100. 300}=100\sqrt{3}\Omega $ khi đó ${{P}_{X\max }}=\dfrac{{{U}^{2}}}{2{{R}_{2}}}=\dfrac{200}{\sqrt{3}}\text{W}$
Câu 24.
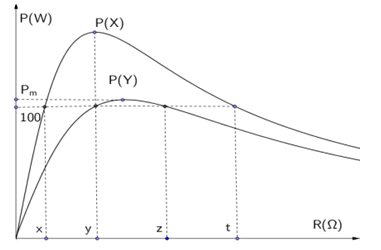
Đặt điện áp $u=U\sqrt{2}\cos (100\pi t+\pi )$lần lượt vào 2 đầu đoạn mạch gồm X và Y. Mỗi mạch đều chứa các phần tử: biến trở R, cuộn cảm thuần L và tụ điện C người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình dưới. Biết rằng: $y+z=400$và $xt=10000$. Xác định gần nhất giá trị \[{{P}_{m}}\]
[A]. $100$
[B]. $110$
[C]. $120$
[D]. $130$
Khi ${{P}_{Y}}=100W\to 100=\dfrac{{{U}^{2}}}{y+z}\to 100=\dfrac{{{U}^{2}}}{400}\to U=200V$
Khi ${{P}_{X}}=100W\to $ có hai giá trị của R thỏa mãn là x và t.
Mà ${{P}_{X\max }}$ khi R=y suy ra: $y=\sqrt{xt}=\sqrt{10000}=100\Omega $ $\to z=300\Omega $ ${{P}_{Y\max }}$ khi ${{R}_{Y\max }}=\sqrt{y. z}=100\sqrt{3}\Omega $ và ${{P}_{Y\max }}=\dfrac{{{U}^{2}}}{2. {{R}_{Y\max }}}=115,5W$
Câu 25.
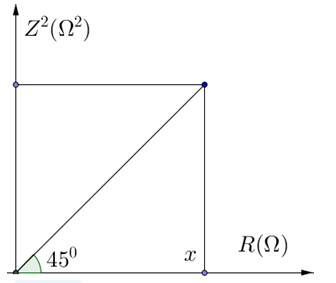
Đặt một điện áp xoay chiều: $u=10\sqrt{2}\cos (100\pi t+\pi )$(V) vào 2 đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ xoay C mắc nối tiếp. Trong quá trình thay đổi R, C, người ta luôn điều chỉnh sao cho công suất tiêu thụ của mạch không đổi và thu được đồ thị như hình dưới. Biết tại $R=x$ thì $Z{}_{C}=50\Omega $. Giá trị công suất đó và cảm kháng lần lượt là:
[A]. 80, 100
[B]. 100, 80
[C]. 50, 100
[D]. 100, 50
Trong quá trình thay đổi R, C, người ta luôn điều chỉnh sao cho công suất tiêu thụ của mạch không đổi Suy ra khi ${{Z}_{L}}={{Z}_{C}}=50\Omega $ công suất đoạn mạch cũng không đổi.
Từ hình vẽ ta có: $\tan \varphi =\tan \dfrac{\pi }{4}=1=\dfrac{{{Z}^{2}}}{R}\to {{Z}^{2}}=R$ $\to {{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}=R\to R=1\Omega $
Công suất khi đó là: $P={{I}^{2}}R=\dfrac{{{U}^{2}}}{{{Z}^{2}}}R=\dfrac{{{10}^{2}}}{1}. 1=100\text{W}$.
Câu 26.
Đặt điện áp $u=220\sqrt{2}\cos (100\pi t)$vào 2 đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Biết rằng biến trở R thay đổi theo giá trị phần chiều dài của nó có dòng điện chạy qua và tuân thủ công thức: $R=2L+10$, (R tính theo $\Omega $ và L tính theo cm). Trong quá trình thay đổi giá trị biến trở, người ta thấy rằng tại L = 13cm hoặc L = 27 cm thì mạch tiêu thụ cùng một giá trị công suất. Giả sử chiều dài L nằm trong đoạn [10; 30] (cm). Giá trị công suất tiêu thụ cực tiểu của mạch điện nói trên gần nhất là:
[A]. 420 W.
[B]. 450 W.
[C]. 470 W.
[D]. 490 W.
Khi L=13cm $\to {{R}_{1}}=2L+10=36\Omega $ và L=27cm $\to {{R}_{1}}=2L+10=64\Omega $ mạch tiêu thụ cùng một giá trị công suất $\to {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}_{1}}{{R}_{2}}=2304({{\Omega }^{2}})$ Khi L=10cm $\to {{R}_{0}}=2L+10=30\Omega $ $\to {{P}_{0}}=\dfrac{{{U}^{2}}}{R_{0}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}. {{R}_{0}}=453,2W$ Khi L=30cm $\to {{R}_{4}}=2L+10=70\Omega $$\to {{P}_{4}}=\dfrac{{{U}^{2}}}{R_{4}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}. {{R}_{4}}=470,2W$ $\Rightarrow {{P}_{\min }}=453,2W$
Câu 27.
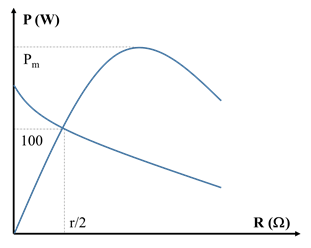
Cho đoạn mạch AB gồm: biến trở R, cuộn cảm thuần L và tụ dung C mắc nối tiếp, với $L=\dfrac{1}{\pi }(H)$, $C=\dfrac{{{10}^{-3}}}{7,2\pi }$(F). Đặt điện áp xoay chiều $u=U\sqrt{2}\cos (120\pi t)$ vào 2 đầu A, B. Hình vẽ bên dưới thể hiện quan hệ giữa công suất tiêu thụ trên AB với điện trở R trong 2 trường hợp: mạch điện AB lúc đầu và mạch điện AB sau khi mắc thêm điện trở r nối tiếp với R. Giá trị \[{{P}_{m}}\] là:
[A]. $\dfrac{200}{\sqrt{3}}$
[B]. $200\sqrt{3}$
[C]. $\dfrac{150}{\sqrt{3}}$
[D]. $100\sqrt{3}$
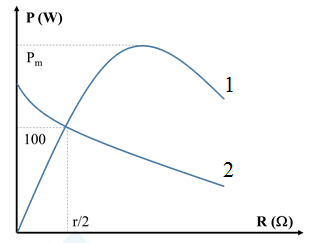
${{Z}_{L}}=120\Omega ;{{Z}_{C}}=60\Omega $
Nhận thấy khi $R=0\Omega $ thì đường 1 có P = 0 nhưng đường 2 có $P\ne 0$ nên đường 1 ứng với công suất khi chưa mắc thêm r.
+ Xét đường 1 tại $R=\dfrac{r}{2}$ ta có: $P={{I}^{2}}. R=\dfrac{{{U}^{2}}}{{{\left( \dfrac{r}{2} \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}. \dfrac{r}{2}\to 100=\dfrac{{{U}^{2}}}{{{\left( \dfrac{r}{2} \right)}^{2}}+{{60}^{2}}}. \dfrac{r}{2}(1)$
+ Xét đường 2 tại $R=\dfrac{r}{2}$ ta có: $P=I{{‘}^{2}}. (R+r)=\dfrac{{{U}^{2}}}{{{\left( \dfrac{r}{2}+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}. \left( \dfrac{r}{2}+r \right)\to 100=\dfrac{{{U}^{2}}}{{{\left( \dfrac{r}{2}+r \right)}^{2}}+{{60}^{2}}}. \left( \dfrac{r}{2}+r \right)(2)$ Từ (1) và (2) suy ra: $r=40\sqrt{3}\Omega $ $\to {{U}^{2}}=\dfrac{24000}{\sqrt{3}}({{V}^{2}})$ + Xét đường 1: ${{P}_{m}}=\dfrac{{{U}^{2}}}{2R}=\dfrac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\dfrac{200}{\sqrt{3}}W. $
Câu 28.
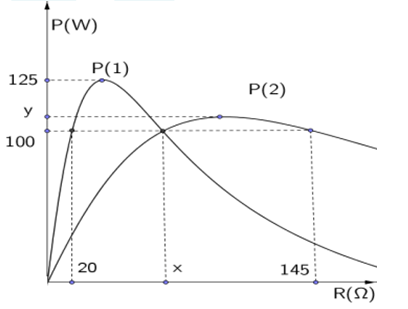
Lần lượt đặt vào 2 đầu đoạn mạch xoay chiều RLC (R là biến trở, L thuần cảm) 2 điện áp xoay chiều: ${{u}_{1}}={{U}_{01}}\cos ({{\omega }_{1}}t+1,32)$ và ${{u}_{2}}={{U}_{02}}\cos ({{\omega }_{2}}t-1,32)$, người ta thu được đồ thị công suất mạch điện xoay chiều toàn mạch theo biến trở R như hình dưới. Giá trị gần nhất của y là:
[A]. 90
[B]. 100
[C]. 110
[D]. 120
+ Xét đường P(1): Ta có: ${{P}_{1\max }}=125\text{W}=\dfrac{U_{1}^{2}}{2. \sqrt{20. x}}(1)$ Khi ${{P}_{1}}=100W=\dfrac{U_{1}^{2}}{20+x}(2)$
Từ (1) và (2) suy ra: $\dfrac{125}{100}=\dfrac{20+x}{2\sqrt{20. x}}\to 125x={{(20+x)}^{2}}\Rightarrow \left[ \begin{align} & x=5\Omega (loai) \\ & x=80\Omega \\ \end{align} \right. \to x=80\Omega $
+ Xét đường P(2): Khi ${{P}_{2}}=100W=\dfrac{U_{2}^{2}}{x+145}\to 100=\dfrac{U_{2}^{2}}{80+145}\Rightarrow {{U}_{2}}=150V$ $\to {{P}_{2\max }}=\dfrac{U_{2}^{2}}{2\sqrt{x. 145}}=\dfrac{{{150}^{2}}}{2\sqrt{80. 145}}=\dfrac{1125}{2\sqrt{29}}=104,45W$
Câu 29.
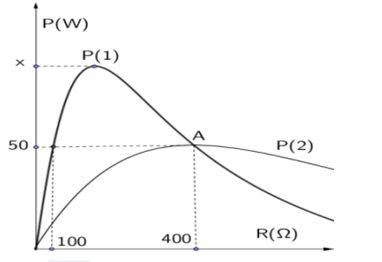
Lần lượt đặt vào 2 đầu đoạn mạch xoay chiều RLC (R là biến trở, L thuần cảm) 2 điện áp xoay chiều: ${{u}_{1}}=U\cos ({{\omega }_{1}}t+\pi )$và ${{u}_{2}}=U\cos ({{\omega }_{2}}t-1,57)$, người ta thu được đồ thị công suất mạch điện xoay chiều toàn mạch theo biến trở R như hình dưới. Biết A là đỉnh của đồ thị P(2). Giá trị của x gần nhất là:
[A]. 60
[B]. 80
[C]. 100
[D]. 90
\[{{P}_{2\max }}=\dfrac{{{U}^{2}}}{2.400}=50\to {{U}^{2}}=400000\]
${{P}_{(1)m\text{ax}}}=\dfrac{{{U}^{2}}}{2\sqrt{{{R}_{1}}. {{R}_{2}}}}=\dfrac{400000}{2\sqrt{100. 400}}=100W$
Câu 30.
Mạch điện xoay chiều mắc nối tiếp gồm biến trở R, cuộn dây thuần cảm L và tụ điện C. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng 100 V và tần số f không đổi. Điều chỉnh để \[R={{R}_{1}}=50\Omega \] thì công suất tiêu thụ của mạch là \[{{P}_{1}}=60W\] và góc lệch pha của điện áp và dòng điện là \[{{\varphi }_{1}}\]. Điều chỉnh để \[R={{R}_{2}}\] thì công suất tiêu thụ của mạch là \[{{P}_{2}}\] và góc lệch pha của điện áp và dòng điện là \[{{\varphi }_{2}}\] với ${{\cos }^{2}}{{\varphi }_{1}}+{{\cos }^{2}}{{\varphi }_{2}}=\dfrac{3}{4}$. Tỉ số $\dfrac{{{P}_{2}}}{{{P}_{1}}}$ bằng
[A]. 1
[B]. 2
[C]. 3
[D]. 4
Ta có: \[{{P}_{1}}=\dfrac{{{U}^{2}}}{{{R}_{1}}}{{\cos }^{2}}{{\varphi }_{1}}\Rightarrow {{\cos }^{2}}{{\varphi }_{1}}=\dfrac{3}{10}\Rightarrow \left\{ \begin{align} & {{\cos }^{2}}{{\varphi }_{2}}=\dfrac{3}{4}-{{\cos }^{2}}{{\varphi }_{1}}=\dfrac{9}{20} \\ & {{Z}_{1}}=\dfrac{R}{\text{cos}{{\varphi }_{1}}}=50\sqrt{\dfrac{10}{3}}\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=\dfrac{17500}{3} \\ \end{align} \right. \] \[{{\cos }^{2}}{{\varphi }_{2}}=\dfrac{9}{20}\Leftrightarrow \dfrac{R_{2}^{2}}{R_{2}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\dfrac{9}{20}\Rightarrow R_{2}^{{}}=\dfrac{50\sqrt{231}}{11}\Omega \] $\Rightarrow {{P}_{2}}=\dfrac{{{U}^{2}}}{{{R}_{2}}}{{\cos }^{2}}{{\varphi }_{2}}\Rightarrow \dfrac{{{P}_{2}}}{{{P}_{1}}}=\dfrac{{{\cos }^{2}}{{\varphi }_{2}}}{{{\cos }^{2}}{{\varphi }_{1}}}. \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{9/20}{3/10}. \dfrac{50}{\dfrac{50\sqrt{231}}{11}}\approx 1$.
Câu 31.
Đoạn mạch R, L, C mắc nối tiếp. Cuộn cảm thuần và R thay đổi được. Đặt giữa hai đầu đoạn mạch AB điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh \[R={{R}_{1}}\] thì công suất trên mạch là \[{{P}_{1}}\] và độ lệch pha giữa cường độ dòng điện và điện áp tức thời hai đầu mạch là $\dfrac{\pi }{4}$. Khi điều chỉnh \[R={{R}_{2}}\] thì công suất trên mạch là \[{{P}_{2}}\] và độ lệch pha giữa cường độ dòng điện và điện áp hai đầu mạch là $\dfrac{\pi }{3}$ . So sánh \[{{P}_{1}}\] và \[{{P}_{2}}\] ta có
[A]. \[{{P}_{1}}>{{P}_{2}}\] .
[B]. ${{P}_{1}}=\dfrac{{{P}_{2}}}{\sqrt{3}}$.
[C]. \[{{P}_{1}}={{P}_{2}}\] .
[D]. \[{{P}_{1}}<{{P}_{2}}\] .
+ Khi \[R={{R}_{1}}\]: $\tan \varphi =\tan \left( \pm \dfrac{\pi }{4} \right)=\pm 1\Rightarrow \left| {{Z}_{L}}-{{Z}_{C}} \right|={{R}_{1}}$ (1) ${{P}_{1}}=\dfrac{{{U}^{2}}}{R_{1}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}. {{R}_{1}}=\dfrac{{{U}^{2}}}{2{{R}_{1}}}$ (*) + Khi \[R={{R}_{2}}\]: $\tan \varphi =\tan \left( \pm \dfrac{\pi }{3} \right)=\pm \sqrt{3}\Rightarrow \left| {{Z}_{L}}-{{Z}_{C}} \right|=\sqrt{3}{{R}_{2}}$ (2) Từ (1) và (2) suy ra: ${{R}_{2}}=\dfrac{{{R}_{1}}}{\sqrt{3}}$ ${{P}_{2}}=\dfrac{{{U}^{2}}}{R_{2}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}. {{R}_{2}}=\dfrac{{{U}^{2}}}{4{{R}_{2}}}=\dfrac{\sqrt{3}{{U}^{2}}}{4{{R}_{1}}}$ (**) So sánh (*) và (**) suy ra: \[{{P}_{1}}>{{P}_{2}}\]