Điện xoay chiều quan hệ tức thời giữa u và i
Dạng 1: quan hệ về thời điểm và thời gian giữa u và i
Câu 1.
Một điện áp xoay chiều có biểu thức $u=220\sqrt{2}\cos \left( 100\pi t+\dfrac{2\pi }{3} \right)$ V (t tính bằng s). Điện áp tức thời tại t = 0 có độ lớn
[A]. $-110\sqrt{2}$ V và đang tăng.
[B]. $-110\sqrt{2}$ V và đang giảm
[C]. $110\sqrt{2}$ V và đang giảm.
[D]. $110\sqrt{2}$ V và đang tăng.
Tại t = 0: $\varphi =\dfrac{2\pi }{3}$
→ $u=-\dfrac{{{U}_{0}}}{2}(-)$ → $\left| u \right|=\dfrac{{{U}_{0}}}{2}(+)=110\sqrt{2}(+)$ .
Câu 2.
Cường độ dòng điện qua một đoạn mạch có biểu thức $i=5\sqrt{2}\cos 100\pi t$ (A) (t tính bằng s). Cường độ dòng điện tức thời tại thời điểm t = 2015 s là
[A]. $-5\sqrt{2}$ A.
[B]. 5A.
[C]. $5\sqrt{2}$ A.
[D]. −5A.
Tại t = 2015s: ${{\phi }_{2015\text{s}}}\equiv 0$ → $i={{I}_{0}}=5\sqrt{2}$A .
Câu 3.
Dòng điện xoay chiều có cường độ $i=4\sqrt{2}\cos \left( 120\pi t+\dfrac{\pi }{3} \right)$(A). Ở thời điểm t = $\dfrac{1}{90}s$, cường độ tức thời của dòng điện này có giá trị
[A]. cực đại.
[B]. $\text{2}\sqrt{\text{2}}\text{ A}$và đang giảm
[C]. $\text{2}\sqrt{\text{2}}\text{ A}$và đang giảm
[D]. $\text{2}\sqrt{\text{2}}\text{ A}$và đang tăng.
Tại t = 0,02s: ${{\phi }_{\dfrac{\text{1}}{90}\text{s}}}=\dfrac{5\pi }{3}\equiv -\dfrac{\pi }{3}$ → $i=\dfrac{{{I}_{0}}}{2}(+)$ .
Câu 4. CĐ2011
Cho dòng điện xoay chiều có tần số 50 Hz chạy qua một đoạn mạch. Khoảng thời gian giữa hai lần liên tiếp cường độ dòng điện này bằng 0 là
[A]. $\dfrac{1}{100}$s.
[B]. $\dfrac{1}{200}$s.
[C]. $\dfrac{1}{50}$s.
[D]. $\dfrac{1}{25}$s.
$\Delta t = \dfrac{T}{2}$
Câu 5.
Một dòng điện xoay chiều cường độ \[i=4\cos \left( 100\pi t-\dfrac{\pi }{4} \right)\](A). Ở thời điểm t = 5 ms cường độ tức thời của dòng điện này có giá trị là
[A]. cực đại
[B]. $\text{2}\sqrt{\text{2}}\text{ A}$ và đang giảm.
[C]. cực tiểu.
[D]. $\text{2}\sqrt{\text{2}}\text{ A}$ và đang tăng.
Tại t = 5ms: ${{\phi }_{\text{5ms}}}=\dfrac{\pi }{4}$ → $i=\dfrac{{{I}_{0}}\sqrt{2}}{2}(-)$
Câu 6.
Cho một dòng điện xoay chiều có cường độ i = 4sin100πt (A), t tính bằng s. Tại thời điểm t0, giá trị của i là $2\sqrt{3}$A và đang tăng. Đến thời điểm sau đó 0,045 s thì giá trị của i là
[A]. − 4 A.
[B]. \[2\sqrt{3}\]A và đang tăng.
[C]. \[2\sqrt{3}\]A và đang tăng.
[D]. 2 A và đang giảm.

Tại t0: $i=\dfrac{{{I}_{0}}\sqrt{3}}{2}(+)$
Sau đó: $\Delta t=0,045\text{ s =}\dfrac{9T}{4}\text{ = 2T + }\dfrac{T}{4}$
→ Sau 2T, dòng điện quay lại trạng thái tại t0, sau đó $\dfrac{T}{4}=\dfrac{T}{12}+\dfrac{T}{6}$ theo trục phân bố thời gian i đến giá trị $\dfrac{{{I}_{0}}}{2}$ và đang giảm.
Câu 7.
Đặt điện áp u = 310cos100πt (V) (t tính bằng s) vào hai đầu một đoạn mạch. Kể từ thời điểm t = 0, điện áp tức thời giữa hai đầu đoạn mạch này đạt giá trị 155 V lần đầu tiên tại thời điểm
[A]. $\dfrac{1}{120}$ s.
[B]. $\dfrac{1}{300}$s.
[C]. $\dfrac{1}{60}$ s .
[D]. $\dfrac{1}{600}$s .
![]()
Tại t = 0: i = I0
Thời điểm đầu tiên $i=155V=\dfrac{{{I}_{0}}}{2}$ là $\dfrac{T}{6}=\dfrac{1}{300}s$ .
Câu 8. CĐ2013
Một dòng điện có cường độ i = I0cos2πft. Tính từ t = 0, khoảng thời gian ngắn nhất để cường độ dòng điện này bằng 0 là 0,004 s. Giá trị của f bằng
[A]. 62,5 Hz.
[B]. 60,0 Hz.
[C]. 52,5 Hz.
[D]. 50,0 Hz.
$\Delta t=0,004\text{s}=\dfrac{T}{4}\to T=0,016\text{s}\to f=62,5\text{ Hz}$.
Câu 9. ĐH2007
Dòng điện chạy qua một đoạn mạch có biểu thức i = I0sin100πt. Trong khoảng thời gian từ 0 đến 0,01s cường độ dòng điện tức thời có giá trị bằng 0,5I0vào những thời điểm
[A]. $\dfrac{1}{300}$s và $\dfrac{2}{300}$. s
[B]. $\dfrac{1}{400}$s và $\dfrac{2}{400}$. s
[C]. $\dfrac{1}{500}$s và $\dfrac{3}{500}$. s
[D]. $\dfrac{1}{600}$s và $\dfrac{5}{600}$. s
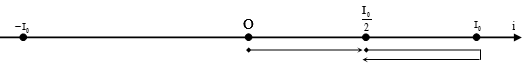
i = I0sin100πt = ${{I}_{0}}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)$ → tại t = 0, i = 0(+).
Theo trục phân bố thời gian trong $0,01\text{s}=\dfrac{T}{2}$s đầu tiên, i có giá trị 0,5I0 tại $\dfrac{T}{12}=\dfrac{1}{600}s$ và $\dfrac{T}{4}+\dfrac{T}{6}=\dfrac{5}{600}s$.
Câu 10.
Biểu thức hiệu điện thế hai đầu một đoạn mạch u = 200cos(ωt) V. Tại thời điểm t, điện áp u = 100 V và đang tăng. Hỏi vào thời điểm \[{t}’=t+\dfrac{T}{4}\] điện áp u có giá trị bằng bao nhiêu ?
[A]. 100 V.
[B]. $100\sqrt{2}\,V.$
[C]. $100\sqrt{3}\,V.$
[D]. –100 V.

Tại t, i = 100(+) = $\dfrac{{{I}_{0}}}{2}(+)$ .
Theo trục phân bố thời gian dễ dàng thấy sau $\dfrac{T}{4}=\dfrac{T}{6}+\dfrac{T}{12}$, dòng điện có $i=\dfrac{{{I}_{0}}\sqrt{3}}{2}$ và đang giảm.
Câu 11. ĐH2011
Tại thời điểm t, điện áp $u=200\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)$ (trong đó u tính bằng V, t tính bằng s) có giá trị $100\sqrt{2}V$ và đang giảm. Sau thời điểm đó$\dfrac{1}{300}s$, điện áp này có giá trị là
[A]. – 100V.
[B]. $100\sqrt{3}V.$
[C]. $-100\sqrt{2}V.$
[D]. 200 V.
Tại t, i = $\dfrac{{{I}_{0}}}{2}(-)$, theo trục phân bố thời gian, sau đó $\dfrac{1}{300}s=\dfrac{T}{6}$ , dòng điện $i=-\dfrac{{{I}_{0}}}{2}(-)$.
Câu 12. CĐ2013
Điện áp ở hai đầu một đoạn mạch là u = 160cos100πt (V) (t tính bằng giây). Tại thời điểm t1, điện áp ở hai đầu đoạn mạch có giá trị là 80 V và đang giảm. Đến thời điểm t2 = t1 + 0,015 s, điện áp ở hai đầu đoạn mạch có giá trị bằng
[A]. $40\sqrt{3}$ V.
[B]. $80\sqrt{3}$ V.
[C]. 40 V.
[D]. 80 V.

Tại t, i = 80(-) = $\dfrac{{{I}_{0}}}{2}(-)$ .
Theo trục phân bố thời gian dễ dàng thấy sau $\Delta t=0,015\text{s}=\dfrac{3T}{4}=\dfrac{T}{3}+\dfrac{T}{4}+\dfrac{T}{6}$, dòng điện có $i=\dfrac{{{I}_{0}}\sqrt{3}}{2}$và đang tăng. .
Câu 13.
Một đèn ống được mắc vào mạng điện xoay chiều có phương trình \[\text{u = 220}\sqrt{\text{2}}\text{cos}\left( 100\pi t-\dfrac{\pi }{2} \right)\](V) (trong đó u tính bằng V, t tính bằng s). Biết rằng đèn sáng mỗi khi điện áp hai đầu đèn có độ lớn không nhỏ hơn $\text{110}\sqrt{\text{2}}\text{ V}$. Khoảng thời gian đèn tắt trong một chu kì là
[A]. $\dfrac{\text{1}}{\text{300}}\text{s}$.
[B]. $\dfrac{\text{1}}{\text{150}}\text{s}$.
[C]. $\dfrac{\text{1}}{\text{75}}\text{s}$.
[D]. $\dfrac{\text{1}}{\text{50}}\text{s}$.

Cứ mỗi chu kì, khoảng thời gian đèn tắt (nét đứt) là $\Delta t=\dfrac{T}{3}=\dfrac{1}{150}s$.
Câu 14.
Mắc vào đèn neon một nguồn điện xoay chiều có biểu thức $u=220\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)$(V). Đèn chỉ sáng khi điện áp đặt vào đèn thoả mãn $\left| u \right|\ge 110\sqrt{2}$ V. Tỉ số khoảng thời gian thời gian đèn sáng so với đèn tắt trong một chu kì của dòng điện bằng
[A]. 2.
[B]. $\dfrac{1}{2}$.
[C]. $\dfrac{2}{3}$.
[D]. $\dfrac{3}{2}$.
Cứ mỗi chu kì, khoảng thời gian đèn tắt (nét đứt) là $\Delta {{t}_{t\grave{e}i}}=\dfrac{T}{3}$, đèn sáng (nét liền) là $\Delta {{t}_{sng}}=\dfrac{2T}{3}$.
Câu 15.
Một chiếc đèn nêôn đặt dưới một điện áp xoay chiều 119 V – 50 Hz. Nó chỉ sáng lên khi điện áp tức thời giữa hai đầu bóng đèn lớn hơn 84 V. Thời gian bóng đèn sáng trong một chu kỳ là bao nhiêu?
[A]. 0,0100 s.
[B]. 0,0133 s.
[C]. 0,0200 s.
[D]. 0,0233 s.
U = 119 V → ${{U}_{0}}\approx 168$V → 84 V = $\dfrac{{{U}_{0}}}{2}$→ Cứ mỗi chu kì đèn sáng (nét liền) là $\Delta {{t}_{sng}}=\dfrac{2T}{3}=\dfrac{1}{75}s$.
Câu 16. CĐ2009
Điện áp giữa hai đầu một đoạn mạch là u = 150cos100πt (V). Cứ mỗi giây có bao nhiêu lần điện áp này bằng không?
[A]. 100 lần.
[B]. 50 lần.
[C]. 200 lần.
[D]. 2 lần.
Cứ mỗi chu kì điện áp này bằng không 2 lần → cứ sau 1s = 50T, điện áp này bằng không 100 lần .
Câu 17.
Một đèn ống mắc trong mạch điện xoay chiều có điện áp \[u={{U}_{0}}\cos 100\pi t\text{(V)}\]. Đèn chỉ sáng khi điện áp ở 2 cực của nó có độ lớn không nhỏ hơn 0,5U0, thì nhận xét nào sau đây là không đúng?
[A]. Mỗi lần đèn tắt kéo dài 1/150(s)
[B]. Mỗi lần đèn tắt kéo dài 1/300(s)
[C]. Trong 1s có 100 lần đèn tắt
[D]. Một chu kỳ có 2 lần đèn tắt
Cứ mỗi chu kì đèn sáng hai lần, tắt cũng hai lần. Do đó C và D đúng. Tính toán A sai!
Câu 18.
Hiệu điện thế giữa hai đầu một đoạn mạch có biểu thức u = Uosin(100πt + $\dfrac{\pi }{2}$) (V). Tại thời điểm t nào sau đây hiệu điện thế tức thời $u = \dfrac{{{U}_{o}}}{\sqrt{2}}$?
[A]. $\dfrac{1}{400}$s.
[B]. $\dfrac{9}{400}$s.
[C]. $\dfrac{7}{400}$s.
[D]. $\dfrac{11}{400}$s.

$u = {U_0}\cos 100\pi t = \dfrac{{{U_0}}}{{\sqrt 2 }} \to \left[ \begin{array}{l} 100\pi t = \dfrac{\pi }{4} + 2k\pi \to t = \dfrac{{1 + 8k}}{{400}}\left( s \right)\\ 100\pi t = – \dfrac{\pi }{4} + 2k\pi \to t = \dfrac{{8k – 1}}{{400}}\left( s \right) \end{array} \right.$
Câu 19.
Dòng điện xoay chiều qua một đoạn mạch có biểu thức $i={{I}_{0}}c\text{os}\left( 120\pi t-\dfrac{\pi }{3} \right)A$. Thời điểm thứ 2018 độ lớn cường độ dòng điện bằng cường độ dòng điện hiệu dụng là:
[A]. 8,15 s
[B]. 8,4 s
[C]. 9,26 s
[D]. 10,3 s
Tại t = 0: $i=\dfrac{{{I}_{0}}}{2}(+)$
$\left| i \right|=I=\dfrac{{{I}_{0}}}{\sqrt{2}}\to i=\pm \dfrac{{{I}_{0}}}{\sqrt{2}}$, mỗi chu kì có 4 lần mà dòng điện $i=\pm \dfrac{{{I}_{0}}}{\sqrt{2}}$→ Tách 2018 = 2016 + 2.
Thời điểm cần tìm là: ${{t}^{/}}=504T+\dfrac{T}{6}+\dfrac{T}{8}\approx 8,4\text{s}$.
Câu 20.
Đặt vào hai đầu đèn ống điện áp xoay chiều $u=250c\text{os}\left( 100\pi t+\pi \right)$V. Biết đèn chỉ sáng khi điện áp tức thời có độ lớn không nhỏ hơn $125\sqrt{2}$V. Kể từ t = 0, thời điểm đèn tắt lần thứ 2016 là
[A]. 20,1525 s
[B]. 10,0675 s
[C]. 20,1475 s
[D]. 10,0725 s

Tại t = 0: u = – U0
Đèn sáng tắt tại $\left| u \right|=125V=\dfrac{{{U}_{0}}\sqrt{2}}{2}$
Cứ mỗi chu kì, đèn tắt 2 lần → tách 2016 = 2014 + 2 → ∆t = 1007T + $\dfrac{T}{2}+\dfrac{T}{8}$ = 20,1525 s.
Câu 21.
Một đèn ống mắc trong mạch điện xoay chiều có điện áp \[u={{U}_{0}}\cos 100\pi t\text{ (V)}\]. Đèn chỉ sáng khi điện áp ở 2 cực của nó có độ lớn không nhỏ hơn 0,5U0. Một máy ghi hình với tốc độ 24 hình/s ghi lại thấy rằng: trong 3 s số tấm hình cho thấy đèn ống không sáng (tối) là
[A]. 24
[B]. 30
[C]. 50
[D]. 100
Một chu kì, khoảng thời gian đèn tối $\dfrac{T}{3}$và sáng là \[\dfrac{2T}{3}\]
→ Trong số số tấm hình chụp được trong 3 s (24.3 = 72) có 72: 3 = 24 bức hình tối.
Câu 22.
Đặt vào hai đầu đèn ống điện áp xoay chiều $u=220\sqrt{2}c\text{os}\left( \dfrac{100\pi t}{3}+\dfrac{\pi }{2} \right)$V. Biết đèn chỉ sáng khi điện áp tức thời có độ lớn không nhỏ hơn $110\sqrt{2}$V. Kể từ t = 0, thời điểm đèn sáng lần thứ 2018 là
[A]. 60,505 s
[B]. 60,515 s
[C]. 30,275 s
[D]. 30,265 s

Tại t = 0: u = 0 (-)
Cứ mỗi chu kì, đèn sáng 2 lần → tách 2018 = 2016 + 2 → ∆t = 1008T + $\dfrac{T}{4}+\dfrac{T}{3}$ = 60,515 s.
Dạng 2: quan hệ giữa các giá trị tức thời u, i trong mạch điện xoay chiều
Câu 23.
Một đoạn mạch AB gồm điện trở thuần, cuộn cảm và tụ điện mắc nối tiếp. M là một điểm trên đoạn mạch AB. Điện áp\[{{u}_{AM}}=100\cos 100\pi t\ \](V) và \[{{u}_{MB}}=100\sqrt{3}\cos (100\pi t-\dfrac{\pi }{2})\](V). Điện áp giữa hai đầu đoạn mạch AB là
[A]. \[{{u}_{AB}}=200\cos (100\pi t+\dfrac{\pi }{6})\ (V).\]
[B]. \[{{u}_{AB}}=200\cos (100\pi t-\dfrac{\pi }{6})\ (V).\]
[C]. \[{{u}_{AB}}=200\cos (100\pi t+\dfrac{\pi }{3})\ (V).\]
[D]. \[{{u}_{AB}}=200\cos (100\pi t-\dfrac{\pi }{3})\ (V).\]
uAB = uAM + uMB = \[200\cos (100\pi t-\dfrac{\pi }{3})\ (V)\].
Câu 24.
Mạch điện xoay chiều không phân nhánh gồm điện trở thuần R, cuộn cảm thuần có cảm kháng ${{Z}_{L}}$và tụ điện có dung kháng ${{Z}_{C}}=2{{Z}_{L}}$. Vào một thời điểm khi hiệu điện thế trên điện trở và trên tụ điện có giá trị tức thời tương ứng là 40V và 30V thì hiệu điện thế giữa hai đầu mạch điện là:
[A]. 50V
[B]. 85V
[C]. 25V
[D]. 55V
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\].
Mà bài cho uC = 30 V → uL = -15 V.
Vậy: u = uR + uL + uC = 55 V .
Câu 25. ĐH2013
Đặt điện áp \[u=220\sqrt{2}c\text{os}100\pi tV\] vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở 20 \[\Omega \], cuộn cảm có độ tự cảm \[\dfrac{0,8}{\pi }H\] và tụ điện có điện dung \[\dfrac{{{10}^{-3}}}{6\pi }F\]. Khi điện áp tức thời giữa hai đầu điện trở bằng \[110\sqrt{3}V\] thì điện áp tức thời giữa hai đầu cuộn cảm có độ lớn bằng:
[A]. 440V
[B]. 330V
[C]. \[440\sqrt{3}V\]
[D]. \[330\sqrt{3}V\]
Câu 26. CĐ2012
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 3 lần dung kháng của tụ điện. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu tụ điện có giá trị tương ứng là 60 V và 20 V. Khi đó điện áp tức thời giữa hai đầu đoạn mạch là
[A]. 20$\sqrt{13}$V.
[B]. 10$\sqrt{13}$V.
[C]. 140 V.
[D]. 20 V.
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-3\].
Mà bài cho uC = 20 V → uL = -60 V.
Vậy: u = uR + uL + uC = 20 V
Câu 27.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 4 lần dung kháng của tụ điện. Tại thời điểm t, điện áp tức thời giữa hai đầu tụ điện có giá trị cực đại là 50 V thì điện áp tức thời giữa hai đầu đoạn mạch là
[A]. 150 V.
[B]. -150 V.
[C]. 200 V.
[D]. -200 V.
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-4\].
Mà bài cho uC = 50 V → uL = -200 V.
uR và uC vuông pha nhau → ${{\left( \dfrac{{{u}_{R}}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{C}}}{{{U}_{0C}}} \right)}^{2}}=1$.
Bài cho uC = UOC = 50 V → uR = 0
Vậy: u = uR + uL + uC = -150 V
Câu 28.
Đặt điện áp tần số 50 Hz vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở 60 \[\Omega \], cuộn cảm có độ tự cảm \[\dfrac{0,2}{\pi }H\] và tụ điện có điện dung \[\dfrac{{{10}^{-3}}}{4\pi }F\]. Khi điện áp tức thời giữa hai đầu cuộn cảm là 20 V thì điện áp tức thời giữa hai đầu đoạn mạch là 40V. Cường độ dòng điện cực đại chạy trong mạch là
[A]. 2 A
[B]. $\sqrt{2}$ A
[C]. \[\sqrt{37}\]A
[D]. \[2\sqrt{37}\]A
R = 60 Ω, ZL = 20 Ω và ZC = 40 Ω
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\].
Mà bài cho uL = 20 V → uC = -40 V.
Lại có u = uR + uL + uC = 40 V → uR = 60 V
uR và uL vuông pha nhau và $\dfrac{{{U}_{0\text{R}}}}{{{U}_{0L}}}=\dfrac{R}{{{Z}_{L}}}=3$ → ${{\left( \dfrac{{{u}_{R}}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{L}}}{{{U}_{0L}}} \right)}^{2}}=1\Rightarrow {{\left( \dfrac{{{u}_{R}}}{3} \right)}^{2}}+u_{L}^{2}=U_{0L}^{2}\to {{U}_{0L}}=20\sqrt{2}$V.
Vậy: ${{I}_{0}}=\dfrac{{{U}_{0L}}}{{{Z}_{L}}}=\sqrt{2}$ A.
Câu 29.
Đặt điện áp xoay chiều $u=100\sqrt{2}\cos \omega t$(V) vào hai đầu đoạn mạch gồm điện trở R mắc nối tiếp với tụ điện có điện dung C (với RCω = 1). Tại thời điểm điện áp tức thời giữa hai đầu điện trở là 50V và đang tăng thì điện áp tức thời giữa hai bản tụ điện là
[A]. $-50\sqrt{3}$V.
[B]. 50 V.
[C]. – 50 V.
[D]. $50\sqrt{3}$V.
RCω = 1 → \[\text{R}={{Z}_{C}}\] → ${{U}_{0\text{R}}}={{U}_{0C}}=\dfrac{{{U}_{0}}}{\sqrt{2}}=100$ V
Khi uR = 50V(+) = $\dfrac{{{U}_{0\text{R}}}}{2}$ → pha uR là ${{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}$
mà uC luôn chậm pha hơn uR góc $\dfrac{\pi }{2}$
→ pha của uC lúc này là ${{\phi }_{{{u}_{C}}}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}$
→ ${{u}_{C}}=-\dfrac{{{U}_{0C}}\sqrt{3}}{2}(-)=-50\sqrt{3}$V.
Câu 30.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết dung kháng của tụ điện bằng 2 lần cảm kháng của cuộn cảm. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu mạch có giá trị tương ứng là 40V và 60V. Khi đó điện áp tức thời giữa hai đầu tụ điện là:
[A]. 20 V.
[B]. – 20 V.
[C]. 40 V.
[D]. – 40 V.
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\to {{u}_{C}}=-2{{u}_{L}}\].
Bài cho uR = 40 V và u = uR + uL + uC = 60 V → uL + uC = 20 V → uL = -20 V và uC = 40V
Câu 31.
Đoạn mạch xoay chiều RLC mắc nối tiếp. Điện áp hiệu dụng ở hai đầu điện trở, hai đầu cuộn cảm thuần và hai đầu tụ điện lần lượt là \[30\sqrt{2}\]V, \[60\sqrt{2}\,V\] và \[90\sqrt{2}\,V\]. Khi điện áp tức thời ở hai đầu điện trở là 30V thì điện áp tức thời ở hai đầu mạch có thể là
[A]. 42,43 V
[B]. 81,96 V
[C]. 60 V
[D]. 90 V
U0R = 60 V; U0L = 120 V; U0R = 180 V
+TH1: ${{u}_{R}}=30(+)=\dfrac{{{U}_{0\text{R}}}}{2}(+)\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}$
uL nhanh pha hơn uR góc $\dfrac{\pi }{2}$ →${{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}+\dfrac{\pi }{2}=\dfrac{\pi }{6}$ → ${{u}_{L}}=\dfrac{{{U}_{0L}}\sqrt{3}}{2}=60\sqrt{3}$ V
uC chậm pha hơn uR góc $\dfrac{\pi }{2}$ →${{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}$ → ${{u}_{C}}=-\dfrac{{{U}_{0C}}\sqrt{3}}{2}=-90\sqrt{3}$ V
→ u = uR + uL + uC = $30-30\sqrt{3}\approx -21,96\text{ V}$.
+TH2: ${{u}_{R}}=30(-)=\dfrac{{{U}_{0\text{R}}}}{2}(-)\to {{\phi }_{{{u}_{R}}}}=\dfrac{\pi }{3}$
uL nhanh pha hơn uR góc $\dfrac{\pi }{2}$ →${{\phi }_{{{u}_{L}}}}=\dfrac{\pi }{3}+\dfrac{\pi }{2}=\dfrac{5\pi }{6}$ → ${{u}_{L}}=\dfrac{{{U}_{0L}}\sqrt{3}}{2}=-60\sqrt{3}$ V
uC chậm pha hơn uR góc $\dfrac{\pi }{2}$ →${{\phi }_{{{u}_{L}}}}=\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{\pi }{6}$ → ${{u}_{C}}=\dfrac{{{U}_{0C}}\sqrt{3}}{2}=90\sqrt{3}$ V
→ u = uR + uL + uC = $30+30\sqrt{3}\approx 81,96\text{ V}$.
Câu 32.
Đặt điện áp xoay chiều có tần số ω vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Biết 2LCω2 = 1. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và hai đầu tụ điện lần lượt là 40V và 60V. Khi đó điện áp tức thời giữa hai đầu đoạn mạch là
[A]. 50 V.
[B]. 55 V.
[C]. 70 V.
[D]. 100 V.
2LCω2 = 1 → 2ZL = ZC
uL và uC luôn dao động ngược pha: \[\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{U}_{0L}}}{{{U}_{0C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\to {{u}_{L}}=-\dfrac{1}{2}{{u}_{C}}=-30\]V.
Vậy u = uR + uL + uC = 70 V.
Câu 33.
Đặt điện áp xoay chiều $u = 100\sqrt{2}\cos \omega t$(V) vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Biết 2ZL = 2R = ZC. Tại thời điểm điện áp tức thời giữa hai đầu cuộn cảm là 50 V và đang tăng thì điện áp tức thời trên điện trở là
[A]. -50 V.
[B]. $-50\sqrt{3}$ V.
[C]. $50\sqrt{3}$V.
[D]. 50 V.
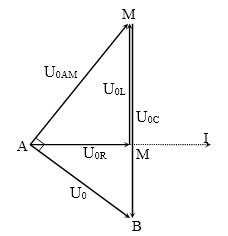
Bài cho U0 = $100\sqrt{2}$V và 2ZL = 2R = ZC → 2U0L = 2U0R = U0C → U0R = 100 V, U0L = 100 V, U0C = 200 V
uL = 50V (+) = $\dfrac{{{U}_{0L}}}{2}(+)\to {{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}\to {{u}_{R}}=-\dfrac{{{U}_{0\text{R}}}\sqrt{3}}{2}(+)=-50\sqrt{3}(+)$
Câu 34.
Một mạch điện gồm cuộn cảm thuần $L=\dfrac{1}{\pi }H$ nối tiếp với điện trở $R=100\Omega .$ Đặt vào hai đầu đoạn mạch điện áp $u=100\sqrt{2}\cos \left( 100\pi t \right)$ Tại thời điểm điện áp tức thời trên điện trở là 50V và đang tăng thì điện áp tức thời trên cuộn cảm thuần là
[A]. $-50\sqrt{3}\,V.$
[B]. $50\sqrt{3}\,V.$
[C]. $50\,V.$
[D]. $-50\,V.$
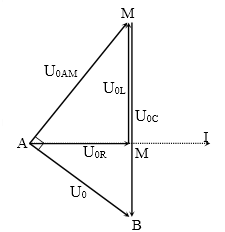
Bài cho U0 = $100\sqrt{2}$V và ZL = R → U0L = U0R = 100 V.
${{u}_{R}}=50(+)=\dfrac{{{U}_{0R}}}{2}(+)\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}\to {{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}+\dfrac{\pi }{2}=\dfrac{\pi }{6}\to {{u}_{L}}=\dfrac{{{U}_{0L}}\sqrt{3}}{2}(-)=50\sqrt{3}(-)$
Câu 35.
Đặt điện áp xoay chiều u = U0cos(πt) (V) luôn ổn định vào hai đầu đọan mạch RLC nối tiếp. Biết điện áp hiệu dụng ở hai đầu điện trở là $40\sqrt{2}$V, hai đầu cuộn cảm thuần là $50\sqrt{2}$V,và hai tụ điện là $90\sqrt{2}$V. Khi điện áp tức thời ở hai đầu điện trở là 40V và đang tăng thì điện áp tức thời ở hai đầu mạch gần bằng nhất là
[A]. 109,28V.
[B]. – 80V .
[C]. – 29,28V.
[D]. 81,96V.
U0R = 80 V; U0L = 100 V; U0R = 180 V
${{u}_{R}}=40(+)=\dfrac{{{U}_{0\text{R}}}}{2}(+)\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}$
uL nhanh pha hơn uR góc $\dfrac{\pi }{2}$ →${{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}+\dfrac{\pi }{2}=\dfrac{\pi }{6}$
→ ${{u}_{L}}=\dfrac{{{U}_{0L}}\sqrt{3}}{2}=50\sqrt{3}$ V
uC chậm pha hơn uR góc $\dfrac{\pi }{2}$
→ ${{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}-\dfrac{\pi }{2}=-\dfrac{5\pi }{6}$ → ${{u}_{C}}=-\dfrac{{{U}_{0C}}\sqrt{3}}{2}=-90\sqrt{3}$ V
→ u = uR + uL + uC = $40-40\sqrt{3}\approx -29,28\text{ V}$.
Câu 36.
Một đoạn mạch điện gồm điện trở R = $50\sqrt{3}$Ω mắc nối tiếp với cuộn thuần cảm có L = 1/2π (H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng 200 V, tần số 50 Hz. Tại thời điểm t, cường độ dòng điện qua mạch có giá trị bằng $\sqrt{2}$A và đang tăng thì điện áp hai đầu mạch sau đó $\dfrac{1}{300}s$ bằng
[A]. $100\sqrt{2}$V
[B]. 0 v
[C]. $100\sqrt{6}$ V
[D]. $-100\sqrt{6}$ V
Bài cho U0 = $200\sqrt{2}$V và ZL = 50 Ω → Z = 100 Ω → ${{I}_{0}}=\dfrac{{{U}_{0}}}{Z}=2\sqrt{2}$A
u nhanh pha hơn i góc: $\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{R}=\dfrac{1}{\sqrt{3}}\to {{\varphi }_{u}}-{{\varphi }_{i}}=\dfrac{\pi }{6}(*)$
Tại thời điểm t: $i=\sqrt{2}(+)=\dfrac{{{I}_{0}}}{2}(+)\to {{\phi }_{i}}=-\dfrac{\pi }{3}$
→ Tại thời điểm t + $\dfrac{1}{300}s$, pha của dòng điện sẽ là $\phi _{i}^{/}=-\dfrac{\pi }{3}+\omega .\Delta t=-\dfrac{\pi }{3}+100\pi .\dfrac{1}{300}=0$
$\xrightarrow{\left( * \right)}\phi _{u}^{/}=\phi _{i}^{/}+\dfrac{\pi }{6}=\dfrac{\pi }{6}\to u=\dfrac{{{U}_{0}}\sqrt{3}}{2}(-)=100\sqrt{6}(-)$.
Câu 37.
Đặt một điện áp xoay chiều u vào hai đầu của một đoạn mạch gồm điện trở R mắc nối tiếp với một tụ điện có điện dung C. Điện áp tức thời hai đầu điện trở R có biểu thức\[{{u}_{R}}=100\cos (2\pi ft+\varphi )(V)\] . Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu đoạn mạch và hai đầu điện trở có giá trị $u=100\sqrt{3}\text{ }V$ và ${{u}_{R}}=50\sqrt{3}\text{ }V$. Điện áp hiệu dụng giữa hai bản tụ điện.
[A]. \[50\sqrt{3}\]V.
[B]. $50\sqrt{6}$V.
[C]. 50 V.
[D]. \[100\sqrt{3}\]V
Bài cho U0R = 100 V
Thời điểm mà uR = $50\sqrt{3}$ V và u = uR + uC = $100\sqrt{3}$ → uC = $50\sqrt{3}$V
uR và uC vuông pha → ${{\left( \dfrac{{{u}_{R}}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{C}}}{{{U}_{0C}}} \right)}^{2}}=1\text{ }\Rightarrow {{\left( \dfrac{50\sqrt{3}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{50\sqrt{3}}{{{U}_{0C}}} \right)}^{2}}=1$
→ U0C = $100\sqrt{3}$ →${{U}_{C}}=50\sqrt{6}$V
Câu 38.
Đặt một điện áp xoay chiều u vào hai đầu của một đoạn mạch gồm điện trở R mắc nối tiếp với một cuộn cảm thuần. Điện áp tức thời hai đầu điện trở R có biểu thức\[{{u}_{R}}=50\sqrt{2}\cos (2\pi ft+\varphi )(V)\] . Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu đoạn mạch và hai đầu điện trở có giá trị \[u=50\sqrt{2}\text{ }V\] và \[{{u}_{R}}=-25\sqrt{2}\text{ }V\]. Điện áp hiệu dụng giữa hai đầu đoạn mạch
[A]. $60\sqrt{3}$V
[B]. 100 V.
[C]. 50 V.
[D]. $50\sqrt{3}$V.
Bài cho U0R = $50\sqrt{2}$V
Thời điểm mà uR = $-25\sqrt{2}$ V và u = uR + uL = $50\sqrt{2}$ → uL = $75\sqrt{2}$V
uR và uL vuông pha → ${{\left( \dfrac{{{u}_{R}}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{C}}}{{{U}_{0L}}} \right)}^{2}}=1\text{ }\Rightarrow {{\left( \dfrac{25\sqrt{2}}{{{U}_{0\text{R}}}} \right)}^{2}}+{{\left( \dfrac{75\sqrt{2}}{{{U}_{0L}}} \right)}^{2}}=1$
→ U0L = $50\sqrt{6}$ V
→${{U}_{0}}=\sqrt{U_{0\text{R}}^{2}+U_{0L}^{2}}=100\sqrt{2}$V → U = 100 V.
Câu 39.
Đặt vào điện áp \[u=120\sqrt{2}\cos 100\pi t\ \ (V)\]vào hai đầu đoạn mạch gồm điện trở R và tụ điện mắc nối tiếp với\[{{Z}_{C}}=\dfrac{R}{\sqrt{3}}\] . Tại thời điểm \[t=\dfrac{1}{150}s\] thì hiệu điện thế trên tụ có giá trị bằng
[A]. \[30\sqrt{6}\ V.\]
[B]. \[30\sqrt{2}\ V.\]
[C]. \[60\sqrt{2}\ V.\]
[D]. \[60\sqrt{6}\ V.\]
\[\text{Z}=\sqrt{{{R}^{2}}+Z_{C}^{2}}=2{{Z}_{C}}\to {{U}_{0}}=2{{U}_{0C}}\to {{U}_{0C}}=60\sqrt{2}\]V.
$\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=-\dfrac{{{Z}_{C}}}{R}=-\dfrac{1}{\sqrt{3}}\to {{\varphi }_{u}}-{{\varphi }_{i}}=-\dfrac{\pi }{6}\to {{\varphi }_{i}}={{\varphi }_{u}}+\dfrac{\pi }{6}=\dfrac{\pi }{6}$
uC chậm pha hơn i góc $\dfrac{\pi }{2}\to {{\varphi }_{{{u}_{C}}}}=\dfrac{\pi }{6}-\dfrac{\pi }{2}=-\dfrac{\pi }{3}$
→ ${{u}_{C}}=60\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{3} \right)$ V
→ tại t = $\dfrac{1}{150}s$: u = $30\sqrt{2}$ V.
Câu 40.
Đặt điện áp xoay chiều \[u={{U}_{0}}\cos (100\pi t)\](V) vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần \[R=100\sqrt{3}\]Ω, cuộn cảm thuần có độ tự cảm $L=\dfrac{2}{\pi }$H và tụ điện có điện dung $C=\dfrac{100}{\pi }$μF. Tại thời điểm khi điện áp tức thời giữa hai đầu đoạn mạch có giá trị bằng một nửa giá trị cực đại thì cường độ dòng điện tức thời trong mạch \[i=0,5\sqrt{3}A.\] Dùng vôn kế nhiệt có điện trở rất lớn để đo hiệu điện thế hai đầu tụ điện thì vôn kế chỉ:
[A]. \[200\,V.\]
[B]. \[100\text{ }V.\]
[C]. \[100\sqrt{2}\text{ }V.\]
[D]. \[50\sqrt{2}\text{ }V.\]
R = $100\sqrt{3}$Ω, ZL = 200 Ω và ZC = 100 Ω → Z = 200 Ω
$\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}=\dfrac{1}{\sqrt{3}}\to {{\varphi }_{u}}-{{\varphi }_{i}}=\dfrac{\pi }{6}$→ u nhanh pha hơn i góc $\dfrac{\pi }{6}$
Khi u = \[\dfrac{{{U}_{0}}}{2}\to {{\phi }_{u}}=\pm \dfrac{\pi }{3}\]
Nếu: \[{{\phi }_{u}}=-\dfrac{\pi }{3}\to {{\phi }_{i}}=-\dfrac{\pi }{3}-\dfrac{\pi }{6}=-\dfrac{\pi }{2}\to i=0\], mà bài cho i = $0,5\sqrt{3}$ A (loại trường hợp này)
Nếu: \[{{\phi }_{u}}=\dfrac{\pi }{3}\to {{\phi }_{i}}=\dfrac{\pi }{3}-\dfrac{\pi }{6}=\dfrac{\pi }{6}\to i=\dfrac{{{I}_{0}}\sqrt{3}}{2}=0,5\sqrt{3}\to {{I}_{0}}=1\]A
→ U0 = I0Z = 200 V → U0C = 100 V
→ Trong trường hợp này vôn kế chỉ UC = $50\sqrt{2}$ V.
Câu 41.
Đặt điện áp xoay chiều \[u=200\sqrt{2}\cos (100\pi t)V\]vào hai đầu đoạn mạch nối tiếp gồm cuộn dây không thuần cảm có độ tự cảm $L=\dfrac{1}{2\pi }H$, điện trở trong $50\sqrt{3}$Ω và tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{\pi }F$ mắc nối tiếp. Tại thời điểm mà điện áp tức thời giữa hai đầu đoạn mạch là $u=100\sqrt{2}$V và đang giảm thì điện áp tức thời giữa hai đầu cuộn dây là
[A]. $100\sqrt{2}$ V.
[B]. $-100\sqrt{2}$ V.
[C]. – 51,8 V.
[D]. $-100\sqrt{6}$ V.
Tổng trở cuộn dây: \[{{\text{Z}}_{d}}=\sqrt{{{r}^{2}}+Z_{L}^{2}}=\] 100 Ω, tổng trở toàn mạch: \[\text{Z}=\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\] 100 Ω
→ Điện áp cực đại trên cuộn dây: U0d = U0 = $200\sqrt{2}$V.
$\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{r}=-\dfrac{1}{\sqrt{3}}\to {{\varphi }_{u}}-{{\varphi }_{i}}=-\dfrac{\pi }{6}$→ u chậm pha hơn i góc $\dfrac{\pi }{6}$
$\tan \left( {{\varphi }_{{{u}_{d}}}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{r}=\dfrac{1}{\sqrt{3}}\to {{\varphi }_{{{u}_{d}}}}-{{\varphi }_{i}}=\dfrac{\pi }{6}$→ ud nhanh pha hơn i góc $\dfrac{\pi }{6}$
ud nhanh pha hơn ud góc $\dfrac{\pi }{3}$ → Khi u = $100\sqrt{2}(-)=\dfrac{{{U}_{0}}}{2}(-)\to {{\phi }_{u}}=\dfrac{\pi }{3}$
$\to {{\phi }_{{{u}_{d}}}}=\dfrac{\pi }{3}+\dfrac{\pi }{3}=\dfrac{2\pi }{3}\to {{u}_{d}}=-\dfrac{{{U}_{0\text{d}}}}{2}(-)=-100\sqrt{2}(-)$.
Câu 42.
Đặt điện áp xoay chiều u = U0cos$\omega $t vào hai đầu đoạn mạch gồm điện trở thuần R và cuộn cảm thuần có cảm kháng ZL mắc nối tiếp. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch; uL , uR tương ứng là điện áp tức thời giữa hai đầu cuộn cảm, giữa hai đầu điện trở, $c\text{os}\varphi $là hệ số công suất của đoạn mạch. Hệ thức nào sau đây sai?
[A]. ${{\left( \dfrac{{{\text{u}}_{\text{L}}}}{{{Z}_{L}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{\text{R}}}}{R} \right)}^{2}}={{I}^{2}}$
[B]. $I=\dfrac{{{U}_{0}}}{\sqrt{2({{R}^{2}}+Z_{L}^{2})}}$.
[C]. $c\text{os}\varphi =\dfrac{R}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}$.
[D]. $u_{L}^{2}+{{i}^{2}}Z_{L}^{2}=I_{0}^{2}Z_{L}^{2}$
${{\left( \dfrac{{{\text{u}}_{\text{L}}}}{{{U}_{0L}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{\text{R}}}}{{{U}_{0R}}} \right)}^{2}}=1\to {{\left( \dfrac{{{\text{u}}_{\text{L}}}}{{{Z}_{L}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{\text{R}}}}{R} \right)}^{2}}=I_{0}^{2}$
Câu 43.
Đặt điện áp \[u=120\cos (100\pi t)\] (V) vào hai đầu một đoạn mạch gồm điện trở thuần R = 60 Ω, cuộn cảm thuần có độ tự cảm \[L=\dfrac{8}{5\pi }H\], tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{\pi }F$mắc nối tiếp. Ở thời điểm t = 30 ms cường độ dòng điện trong mạch có giá trị là
[A]. $-\sqrt{2}$ A.
[B]. -1,0 A.
[C]. 1 A.
[D]. $\sqrt{2}$ A.
Dễ dàng viết được phương trình dòng điện: $i=\sqrt{2}\cos \left( 100\pi t-\dfrac{\pi }{4} \right)$
→ tại $t=30m\text{s}:{{\phi }_{i}}=\dfrac{3\pi }{4}\to i=-\dfrac{{{I}_{0}}\sqrt{2}}{2}=-1\text{A(-)}$.
Câu 44.
Đặt điện áp \[u={{U}_{0}}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)(V)\]vào hai đầu một đoạn mạch gồm điện trở thuần \[R=40\]Ω và cuộn cảm thuần có độ tự cảm\[\dfrac{0,4}{\pi }H\], mắc nối tiếp. Ở thời điểm t = 0,1 s dòng điện trong mạch có cường độ \[i=-2,75\sqrt{2}\] A. Giá trị của \[{{U}_{0}}\] bằng
[A]. 220V.
[B]. \[220\sqrt{2}\] V.
[C]. 110 V.
[D]. 110\[\sqrt{2}\]V.
$\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{R}=1\to {{\varphi }_{u}}-{{\varphi }_{i}}=\dfrac{\pi }{4}\to {{\varphi }_{i}}=-\dfrac{3\pi }{4}$
→ \[i = {I_0}\cos \left( {100\pi t – \dfrac{{3\pi }}{4}} \right)A.\]
→ tại $t=0,1\text{ s}:{{\phi }_{i}}\equiv -\dfrac{3\pi }{4}\to i=-\dfrac{{{I}_{0}}\sqrt{2}}{2}=-2,75\sqrt{2}\to {{\text{I}}_{0}}=5,5A$
→ U0 = I0Z = $220\sqrt{2}$V.
Câu 45.
Điện áp u = U0cos(100πt) (V) được đặt vào hai đầu đoạn mạch gồm cuộn dây có độ tự cảm $L=\dfrac{0,15}{\pi }$ H và điện trở \[r=5\sqrt{3}\]Ω, và tụ điện có điện dung $C=\dfrac{{{10}^{-3}}}{\pi }$ F mắc nối tiếp. Tại thời điểm t1 điện áp tức thời hai đầu cuộn dây có giá trị 15 V, đến thời điểm t2 = t1 + $\dfrac{1}{75}$(s) thì điện áp tức thời hai đầu tụ điện cũng có giá trị là 15 V. Giá trị của U0 bằng
[A]. 15 V.
[B]. 30 V.
[C]. \[15\sqrt{3}\] V.
[D]. \[10\sqrt{3}\] V.
Câu 46.
Một đoạn mạch điện xoay chiều chỉ có điện trở R và tụ điện C với \[\text{R}={{Z}_{C}}\sqrt{3}\]. Điện áp hai đầu mạch có biểu thức \[u=200\cos \left( 100\pi t+\dfrac{\pi }{3} \right)V\]. Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu điện trở có giá trị bằng 150 V và đang giảm thì điện áp giữa hai đầu tụ điện là
[A]. $50\sqrt{2}$V.
[B]. $50\sqrt{3}$V.
[C]. 50 V.
[D]. \[-50\sqrt{6}\]V
\[\text{Z}=\sqrt{{{R}^{2}}+Z_{C}^{2}}=2{{Z}_{C}}\to {{U}_{0}}=2{{U}_{0C}}\to {{U}_{0C}}=100\]V; U0R = $100\sqrt{3}$ V
Khi ${{u}_{R}}=150(-)=\dfrac{{{U}_{0\text{R}}}\sqrt{3}}{2}(-)\to {{\phi }_{{{u}_{R}}}}=\dfrac{\pi }{6}\to {{\phi }_{{{u}_{C}}}}=-\dfrac{\pi }{3}\to {{u}_{C}}=\dfrac{{{U}_{0C}}}{2}(+)=50V(+)$
Câu 47.
Một đoạn mạch điện xoay chiều chỉ có điện trở và tụ điện mắc nối tiếp. Điện áp hai đầu mạch có biểu thức \[u=100\sqrt{2}\cos \left( 100\pi t \right)V\]thì điện áp hiệu dụng giữa hai đầu điện tụ điện là 60 V. Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu điện trở có giá trị bằng $40\sqrt{2}$V thì điện áp giữa hai đầu đoạn mạch có thể là
[A]. 125 V.
[B]. 130 V.
[C]. 115 V.
[D]. 110 V
U0C = $60\sqrt{2}$ V → U0R = $80\sqrt{2}$ V
Khi ${{u}_{R}}=40\sqrt{2}=\dfrac{{{U}_{0\text{R}}}}{2}\to {{\phi }_{{{u}_{R}}}}=\pm \dfrac{\pi }{3}$
Nếu ${{\phi }_{{{u}_{R}}}}=\dfrac{\pi }{3}\to {{\phi }_{{{u}_{C}}}}=-\dfrac{\pi }{6}\to {{u}_{C}}=\dfrac{{{U}_{0C}}\sqrt{3}}{2}=30\sqrt{6}$V
→ u = uR + uC = 130 V.
Nếu ${{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{3}\to {{\phi }_{{{u}_{C}}}}=-\dfrac{5\pi }{6}\to {{u}_{C}}=-\dfrac{{{U}_{0C}}\sqrt{3}}{2}=-30\sqrt{6}$V
→ u = uR + uC = -16,9 V.
Câu 48.
Đặt điện áp $u=240\sqrt{2}\cos \left( 100\pi t \right)$V vào hai đầu đoạn mạch RLC mắc nối tiếp. Biết R = 60 Ω, cuộn cảm thuần có độ tự cảm $\dfrac{1,2}{\pi }$H và tụ điện có điện dung $\dfrac{{{10}^{-3}}}{6\pi }$F. Khi điện áp tức thời giữa hai đầu cuộn cảm bằng 240 V thì độ lớn của điện áp tức thời giữa hai đầu điện trở và giữa hai bản tụ điện lần lượt bằng
[A]. 240 V; 120 V
[B]. $120\sqrt{2}$V; 120 V
[C]. $120\sqrt{3}$ V; 120 V
[D]. $120\sqrt{3}$V ; $120\sqrt{3}$V
U0 = $240\sqrt{2}$V, ZL = 120 Ω, ZC = 60 Ω → Z = $60\sqrt{2}$Ω → U0R = 240 V, U0L = 480 V, U0C = 240 V
Luôn có: $\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-2\to {{u}_{C}}=-120V$
Khi ${{u}_{L}}=240=\dfrac{{{U}_{0L}}}{2}\to {{\phi }_{{{u}_{L}}}}=\pm \dfrac{\pi }{3}$
+ Nếu ${{\phi }_{{{u}_{L}}}}=\dfrac{\pi }{3}\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{6}\to {{u}_{R}}=\dfrac{{{U}_{0\text{R}}}\sqrt{3}}{2}=120\sqrt{3}\text{ }V$
+ Nếu ${{\phi }_{{{u}_{L}}}}=-\dfrac{\pi }{3}\to {{\phi }_{{{u}_{R}}}}=-\dfrac{5\pi }{6}\to {{u}_{R}}=-\dfrac{{{U}_{0\text{R}}}\sqrt{3}}{2}=-120\sqrt{3}\text{ }V$
Vậy uR trong hai trường hợp luôn có độ lớn là $\left| {{u}_{R}} \right|=120\sqrt{3}$ V.
Câu 49.
Đặt điện áp $u=100\cos \left( 100\pi t-\dfrac{\pi }{4} \right)$ V vào hai đầu đoạn mạch RLC mắc nối tiếp. Biết R = 50 Ω cuộn cảm thuần có độ tự cảm $L=\dfrac{1}{\pi }$H và tụ điện có điện dung $C=\dfrac{{{10}^{-3}}}{5\pi }$F. Khi điện áp tức thời giữa hai đầu cuộn cảm bằng 100 V và đang giảm thì độ lớn của điện áp tức thời giữa hai đầu điện trở và giữa hai bản tụ điện lần lượt bằng
[A]. – 50 V ; $50\sqrt{3}$V
[B]. 50 V ; – 50 V
[C]. $-50\sqrt{3}$ V ; – 50 V
[D]. 50 V ; – 100 V
U0 = 100 V, ZL = 100 Ω, ZC = 50 Ω → Z = $50\sqrt{2}$Ω → U0R = $50\sqrt{2}$V, U0L = $100\sqrt{2}$V, U0C = $50\sqrt{2}$V
Luôn có: $\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-2\to {{u}_{C}}=-50V$
Lại có ${{u}_{L}}=100(-)=\dfrac{{{U}_{0L}}\sqrt{2}}{2}(-)\to {{\phi }_{{{u}_{L}}}}=\dfrac{\pi }{4}\to {{\phi }_{{{u}_{R}}}}=-\dfrac{\pi }{4}\to {{u}_{R}}=\dfrac{{{U}_{0\text{R}}}\sqrt{2}}{2}=50$V
Câu 50.
Cho một đoạn mạch điện xoay chiều có tần số 50 Hz, chỉ có cuộn cảm thuần với cảm kháng là 50 Ω. Tại thời điểm t1 cường độ dòng điện qua mạch là – 1 A, hỏi sau đó 0,015 s thì điện áp hai đầu cuộn cảm bằng
[A]. – 50 V
[B]. $50$ V
[C]. – 100 V
[D]. 100 V
Tại t1, gọi pha dòng điện là ${{\phi }_{i1}}$ → ${{i}_{1}}=-1\text{A}={{I}_{0}}\cos {{\phi }_{i1}}$ (*)
Tại t2, pha dòng điện là: ${{\phi }_{i2}}={{\phi }_{i1}}+\omega \Delta t={{\phi }_{i1}}+\dfrac{3\pi }{2}$ → pha điện áp trên cuộn cảm: ${{\phi }_{u2}}={{\phi }_{i2}}+\dfrac{\pi }{2}={{\phi }_{i1}}+2\pi \equiv {{\phi }_{i1}}$
→ ${{u}_{2}}={{U}_{0}}\cos {{\phi }_{u2}}={{U}_{0}}\cos {{\phi }_{i1}}$ (**)
Từ (*) và (**) → $\dfrac{{{u}_{2}}}{{{i}_{1}}}=\dfrac{{{U}_{0}}}{{{I}_{0}}}={{Z}_{L}}\Rightarrow {{u}_{2}}=-50V$.
Câu 51.
Đặt một điện áp xoay chiều có giá trị hiệu dụng là U vào hai đầu đoạn mạch RL mắc nối tiếp, cuộn cảm thuần. Biết điện trở có giá trị gấp 3 lần cảm kháng. Gọi uR và uL lần lượt là điện áp tức thời ở hai đầu điện trở R và ở hai đầu cuộn cảm thuần ở cùng một thời điểm. Hệ thức đúng là
[A]. $90u_{R}^{2}+10u_{L}^{2}=9{{U}^{2}}$
[B]. $45u_{R}^{2}+5u_{L}^{2}=9{{U}^{2}}$
[C]. $5u_{R}^{2}+45u_{L}^{2}=9{{U}^{2}}$
[D]. $10u_{R}^{2}+10u_{L}^{2}=9{{U}^{2}}$
R = 3ZL → U0R = 3U0L → ${{U}_{0}}=\sqrt{U_{0\text{R}}^{2}+U_{0L}^{2}}={{U}_{0L}}\sqrt{10}$
→ ${{U}_{0L}}=\dfrac{{{U}_{0}}}{\sqrt{10}};{{U}_{0\text{R}}}=\dfrac{3{{U}_{0}}}{\sqrt{10}}$
uR và uL vuông pha → ${{\left( \dfrac{{{\text{u}}_{\text{L}}}}{{{U}_{0L}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{\text{R}}}}{{{U}_{0R}}} \right)}^{2}}=1\to {{\left( \dfrac{{{\text{u}}_{\text{L}}}}{\dfrac{{{U}_{0}}}{\sqrt{10}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{\text{R}}}}{\dfrac{3{{U}_{0}}}{\sqrt{10}}} \right)}^{2}}=1\to 45u_{L}^{2}+5u_{R}^{2}=9{{U}^{2}}$.
Câu 52.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch RLC (L thuần cảm) nối tiếp. Biết điện áp hai đầu đoạn mạch lệch pha so với cường độ dòng điện trong mạch là φ. Ở thời điểm t bất kì, điện áp tức thời trên đoạn mạch chứa LC và trên R lần lượt là uLC và uR. Điện áp cực đại trên điện trở R là
[A]. ${{U}_{0R}}={{u}_{LC}}\cos \varphi +{{u}_{R}}\sin \varphi $
[B]. ${{U}_{0R}}={{u}_{LC}}\sin \varphi +{{u}_{R}}\cos \varphi $
[C]. $U_{0R}^{2}=u_{LC}^{2}+{{\left( \dfrac{{{u}_{R}}}{\tan \varphi } \right)}^{2}}$
[D]. $U_{0R}^{2}=u_{R}^{2}+{{\left( \dfrac{{{u}_{LC}}}{\tan \varphi } \right)}^{2}}$
$\tan \varphi =\dfrac{{{U}_{0L}}-{{U}_{0C}}}{{{U}_{0\text{R}}}}=\dfrac{{{U}_{0LC}}}{{{U}_{0\text{R}}}}$
uLC và uR luôn vuông pha → ${{\left( \dfrac{{{\text{u}}_{R}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{LC}}}{{{U}_{0LC}}} \right)}^{2}}=1\to {{\left( \dfrac{{{\text{u}}_{R}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{LC}}}{{{U}_{0R}}\tan \varphi } \right)}^{2}}=1\to u_{R}^{2}+{{\left( \dfrac{{{\text{u}}_{LC}}}{\tan \varphi } \right)}^{2}}=U_{0\text{R}}^{2}$
Câu 53.
Đặt một điện áp xoay chiều ổn định vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần R ; cuộn cảm thuần và tụ điện. Tại thời điểm t1 các giá trị tức thời của điện áp hai đầu cuộn dây và hai đầu điện trở R lần lượt là uL =$-20\sqrt{3}$V; uR = 30 V. Tại thời điểm t2 các giá trị tức thời là $u_{L}^{/} = 40$V; $u_{C}^{/} = -120$V,$u_{R}^{/}=0$. Điện áp cực đại giữa hai đầu đoạn mạch là
[A]. 100 V.
[B]. 120 V.
[C]. $80\sqrt{3}$V.
[D]. 60 V.
Do uR vuông pha với cả uL và uC
Xét tại t2: $u_{R}^{/}=0$→ \[\left| u_{L}^{/} \right|={{U}_{0L}}\]= 40 V; \[\left| u_{C}^{/} \right|={{U}_{0C}}=120\text{ V}\]
Lại có: $\dfrac{u_{L}^{/}}{u_{C}^{/}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{3}\to {{Z}_{C}}=3{{\text{Z}}_{L}}\to {{U}_{0C}}=3{{U}_{0L}}$
Xét tại t1: ${{\left( \dfrac{{{\text{u}}_{\text{R}}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{L}}}{{{U}_{0L}}} \right)}^{2}}=1\to {{U}_{0\text{R}}}=60V$
Vậy: ${{U}_{0}}=\sqrt{U_{0\text{R}}^{2}+{{\left( {{U}_{0L}}-{{U}_{0C}} \right)}^{2}}}=100V$.
Câu 54.
Đặt điện áp $u={{U}_{0}}\cos 100\pi t$(V) vào hai đầu đoạn mạch AB theo thứ tự gồm RLC nối tiếp (cuộn dây thuần cảm), M là điểm nối giữa R và L. Điện áp tức thời của đoạn mạch AM(chứa R) và MB(chứa L và C) tại thời điểm t1 là ${{u}_{AM1}}=60\,\text{ }V;\,\,{{u}_{MB1}}=15\sqrt{7}\text{ }V$ và tại thời điểm t2 là ${{u}_{AM2}}=40\sqrt{3}\,\text{ }V;\,\,{{u}_{MB2}}=30\text{ }V.$ Giá trị của${{U}_{0}}$bằng
[A]. \[100\,V.\]
[B]. $50\sqrt{2}\,V.$
[C]. \[25\sqrt{2}\,\,V.\]
[D]. \[100\sqrt{2}\,V.\]
Do uAM vuông pha với uMB → ${{\left( \dfrac{{{\text{u}}_{\text{AM}}}}{{{U}_{0AM}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{MB}}}{{{U}_{0MB}}} \right)}^{2}}=1$
Xét tại t1: ${{\left( \dfrac{\text{60}}{{{U}_{0AM}}} \right)}^{2}}+{{\left( \dfrac{15\sqrt{7}}{{{U}_{0MB}}} \right)}^{2}}=1$
Xét tại t2: \[{{\left( \dfrac{40\sqrt{3}}{{{U}_{0AM}}} \right)}^{2}}+{{\left( \dfrac{30}{{{U}_{0MB}}} \right)}^{2}}=1\]
Giải hệ hai phương trình, rút ra: U0AM = 80 V, U0MB = 60 V
→ ${{U}_{0}}=\sqrt{U_{0\text{A}M}^{2}+U_{0MB}^{2}}=100\text{ V}$.
Câu 55.
Mạch điện xoay chiều AB mắc nối tiếp theo thức tự gồm điện trở thuần, cuộn thuần cảm và tụ điện. M là điểm nối giữa cuộn cảm thuần và tụ điện. Điện áp giữa hai đầu AM luôn vuông pha với điện áp giữa hai đầu đoạn mạch. Điện áp hiệu dụng trên điện trở là 100 V. Thời điểm mà điện áp tức thời hai đầu đoạn mạch là $100\sqrt{6}$V thì điện áp tức thời trên tụ là $\dfrac{200\sqrt{6}}{3}$V. Điện áp hiệu dụng hai đầu đoạn mạch là
[A]. 240 V.
[B]. 400 V.
[C]. 200 V.
[D]. $\dfrac{200\sqrt{3}}{3}$V.
u = uAM + uC → uAM = $100\sqrt{\dfrac{2}{3}}$ V
u vuông pha với uAM: \[{{\left( \dfrac{u}{{{U}_{0}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{AM}}}{{{U}_{0AM}}} \right)}^{2}}=1\](*)
Lại có \[\dfrac{1}{U_{0R}^{2}}=\dfrac{1}{U_{0}^{2}}+\dfrac{1}{U_{0AM}^{2}}\] (**)
Giải ra: U0 = $200\sqrt{2}$ V → U = 200 V.
Câu 56.
Mạch điện xoay chiều AB mắc nối tiếp theo thức tự gồm điện trở thuần, cuộn thuần cảm và tụ điện. M là điểm nối giữa cuộn cảm thuần và tụ điện. Điện áp giữa hai đầu AM luôn vuông pha với điện áp giữa hai đầu đoạn mạch. Điện áp cực đại trên điện trở là 12a. Khi điện áp tức thời hai đầu đoạn mạch là 16a thì điện áp tức thời trên tụ là 7a. Chọn hệ thức đúng
[A]. 4R = 3ωL.
[B]. 3R = 4ωL.
[C]. R = 2ωL.
[D]. 2R = ωL.
u = uAM + uC → uAM = 9a
u vuông pha với uAM: \[{{\left( \dfrac{16a}{{{U}_{0}}} \right)}^{2}}+{{\left( \dfrac{9\text{a}}{{{U}_{0AM}}} \right)}^{2}}=1\](*)
Lại có \[\dfrac{1}{U_{0R}^{2}}=\dfrac{1}{U_{0}^{2}}+\dfrac{1}{U_{0AM}^{2}}\] với U0R = 12a (**)
Giải ra: U0 = 20a và U0AM = 15a.
Mà theo giản đồ: $\dfrac{{{U}_{0\text{R}}}}{{{U}_{0L}}}=\dfrac{{{U}_{0}}}{{{U}_{0\text{A}M}}}=\dfrac{4}{3}$
→ 3U0R = 4U0L → 3R = 4ZL.
Câu 57.
Mạch điện xoay chiều mắc nối tiếp gồm điện trở thuần R và tụ điện có điện dung C mắc nối tiếp. Dung kháng tụ điện trong mạch là 50 Ω. Biết tại thời điểm t bất kì, điện áp tức thời giữa hai đầu điện trở là uR (V) thì điện áp tức thời giữa hai đầu tụ điện là uC (V) luôn thỏa mãn $9u_{C}^{2}+4u_{R}^{2}=c$, c là một hằng số. Điện trở R có giá trị
[A]. 60 Ω.
[B]. 75 Ω.
[C]. 40 Ω.
[D]. 50 Ω.
uR và uC vuông pha → \[{{\left( \dfrac{{{u}_{C}}}{{{U}_{0C}}} \right)}^{2}}+{{\left( \dfrac{{{u}_{R}}}{{{U}_{0R}}} \right)}^{2}}=1\]
mà bài cho: $9u_{C}^{2}+4u_{R}^{2}=c\Leftrightarrow \dfrac{u_{C}^{2}}{\dfrac{c}{9}}+\dfrac{u_{R}^{2}}{\dfrac{c}{4}}=1$
→ $\dfrac{{{U}_{0C}}}{{{U}_{0R}}}=\dfrac{2}{3}=\dfrac{{{Z}_{C}}}{R}\to R=75$Ω.
Câu 58.
Đặt một điện áp xoay chiều có giá trị hiệu dụng là U vào hai đầu đoạn mạch RLC (L thuần cảm) mắc nối tiếp. Khi điện áp tức thời giữa hai đầu điện trở là 0 thì điện áp tức thời giữa hai đầu cuộn cảm bằng -90 V và điện áp tức thời giữa hai đầu tụ điện là 180 V. Khi điện áp tức thời giữa hai đầu điện trở là $60\sqrt{3}$V thì điện áp tức thời giữa hai đầu cuộn cảm bằng 45 V. Giá trị U là
[A]. \[60\sqrt{2}\]V
[B]. 120 V
[C]. $75\sqrt{2}$ V
[D]. $90\sqrt{2}$ V
Do uR vuông pha với cả uL và uC
Khi: ${{u}_{R}}=0$→ \[\left| {{u}_{L}} \right|={{U}_{0L}}\]= 90 V; \[\left| {{u}_{C}} \right|={{U}_{0C}}=180\text{ V}\]
Lại có: $\dfrac{u_{L}^{/}}{u_{C}^{/}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\to {{Z}_{C}}=2{{\text{Z}}_{L}}\to {{U}_{0C}}=2{{U}_{0L}}$
Lại có:${{\left( \dfrac{\text{60}\sqrt{3}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{45}{{{U}_{0L}}} \right)}^{2}}=1\to {{U}_{0\text{R}}}=120V$
Vậy: ${{U}_{0}}=\sqrt{U_{0\text{R}}^{2}+{{\left( {{U}_{0L}}-{{U}_{0C}} \right)}^{2}}}=150$V → U = $75\sqrt{2}$ V.
Câu 59.
Đặt vào hai đầu đoạn mạch gồm điện trở mắc nối tiếp với tụ điện một điện áp xoay chiều có tần số 50 Hz. Khi điện áp tức thời giữa hai đầu điện trở là $20\sqrt{7}$V thì cường độ dòng điện tức thời là $\sqrt{7}$A và điện áp tức thời giữa hai đầu tụ điện là 45 V. Khi điện áp tức thời giữa hai đầu điện trở là $40\sqrt{3}$V thì điện áp giữa hai đầu tụ điện là 30 V. Điện dung của tụ điện là
[A]. $\dfrac{{{3.10}^{-3}}}{8\pi }F$
[B]. $\dfrac{{{2.10}^{-3}}}{3\pi }F$
[C]. $\dfrac{{{10}^{-4}}}{\pi }F$
[D]. $\dfrac{{{10}^{-3}}}{8\pi }F$
Do uR vuông pha với uC → ${{\left( \dfrac{{{\text{u}}_{R}}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{C}}}{{{U}_{0C}}} \right)}^{2}}=1$
Xét tại t: ${{\left( \dfrac{20\sqrt{7}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{45}{{{U}_{0C}}} \right)}^{2}}=1$(*);
uR và i luôn cùng pha nên tại thời điểm này: $\dfrac{{{u}_{R1}}}{{{i}_{1}}}=R=$ 20 Ω
Xét tại t’: ${{\left( \dfrac{40\sqrt{3}}{{{U}_{0R}}} \right)}^{2}}+{{\left( \dfrac{30}{{{U}_{0C}}} \right)}^{2}}=1$(**)
Giải hệ (*) và (**) ta có: U0R = 80 V và U0C = 60 V → $\dfrac{{{U}_{0C}}}{{{U}_{0\text{R}}}}=\dfrac{{{Z}_{C}}}{R}=\dfrac{3}{4}$
→ ZC = 15 Ω → C = $\dfrac{1}{\omega C}=\dfrac{1}{1500\pi }$ F
Câu 60.
Đặt điện áp xoay chiều $u=100\sqrt{2}\cos 100\pi t$(V) vào hai đầu đoạn mạch RL mắc nối tiếp. Biết điệp áp hiệu dụng giữa hai đầu cuộn cảm thuần là 60 V. Tại thời điểm t1, điện áp hai đầu cuộn cảm là $30\sqrt{2}$V và đang giảm. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\dfrac{1}{600}s$, điện áp giữa hai đầu điện trở có giá trị là
[A]. 80 V
[B]. $-40\sqrt{2}$V
[C]. $40\sqrt{3}$V
[D]. $80\sqrt{2}$V
U0L = $60\sqrt{2}$ V → U0R = $80\sqrt{2}$ V
Xét tại t1: ${{u}_{L1}}=30\sqrt{2}(-)=\dfrac{{{U}_{0L}}}{2}(-)\to {{\phi }_{{{u}_{L1}}}}=\dfrac{\pi }{3}$
→ tại ${{t}_{2}}={{t}_{1}}+\dfrac{1}{600}s$, pha uL là: \[{{\phi }_{{{u}_{L2}}}}={{\phi }_{{{u}_{L1}}}}+\omega \Delta t=\dfrac{\pi }{3}+\dfrac{\pi }{6}=\dfrac{\pi }{2}\to {{\phi }_{{{u}_{R2}}}}={{\phi }_{{{u}_{L2}}}}-\dfrac{\pi }{2}=0\to {{u}_{R2}}={{U}_{0R}}=80\sqrt{2}\]V
Câu 61.
Đoạn mạch xoay chiều AB chứa 3 linh kiện R, L, C. Đoạn AM chứa L, MN chứa R, NB chứa C, R = 50Ω; \[{{Z}_{L}}=50\sqrt{3}\]Ω, ${{Z}_{C}}=\dfrac{50}{\sqrt{3}}$ Ω. Khi \[{{u}_{AN}}=80\sqrt{3}\]V thì uMB = 60 V. Giá trị cực đại điện áp giữa hai đầu đoạn mạch là
[A]. 150 V.
[B]. 100 V.
[C]. \[50\sqrt{7}\]V.
[D]. \[100\sqrt{3}\]V.
$\tan \left( {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{R}=\sqrt{3}\to {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}}=\dfrac{\pi }{3}$: uAN nhanh pha hơn i góc $\dfrac{\pi }{3}$
$\tan \left( {{\varphi }_{{{u}_{MB}}}}-{{\varphi }_{i}} \right)=-\dfrac{{{Z}_{L}}}{R}=-\dfrac{1}{\sqrt{3}}\to {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}}=-\dfrac{\pi }{6}$: uMBchậm pha hơn i góc $-\dfrac{\pi }{6}$
uAN nhanh pha uMB một góc $\dfrac{\pi }{2}$ (vuông pha)
→ ${{\left( \dfrac{{{\text{u}}_{AM}}}{{{U}_{0AM}}} \right)}^{2}}+{{\left( \dfrac{{{\text{u}}_{MB}}}{{{U}_{0MB}}} \right)}^{2}}=1\Rightarrow {{\left( \dfrac{80\sqrt{3}}{{{U}_{0AM}}} \right)}^{2}}+{{\left( \dfrac{60}{{{U}_{0MB}}} \right)}^{2}}=1$(*)
Mà \[{{\text{Z}}_{AN}}=\sqrt{{{R}^{2}}+Z_{L}^{2}}=100\]Ω, \[{{\text{Z}}_{MB}}=\sqrt{{{R}^{2}}+Z_{C}^{2}}=\dfrac{100}{\sqrt{3}}\]
→ $\dfrac{{{U}_{0\text{A}M}}}{{{U}_{0MB}}}=\dfrac{{{Z}_{AM}}}{{{Z}_{MB}}}=\sqrt{3}$,
thế vào (*), ta có: ${{U}_{0MB}}=100$ V
→ ${{U}_{0\text{AN}}}=100\sqrt{3}$V → $\dfrac{{{U}_{0\text{R}}}}{{{U}_{0\text{A}N}}}=\dfrac{R}{{{Z}_{AN}}}=\dfrac{50}{100}\to {{U}_{0\text{R}}}=50\sqrt{3}$V
→ U0L = 150 V → U0C = 50 V.
→ U0 = $50\sqrt{7}$V
Câu 62.
Đặt điện áp$u=U\sqrt{2}\cos 100\pi t$(V) vào hai đầu một mạch điện xoay chiều gồm cuộn cảm thuần độ tự cảm L = 0,5/π (H) mắc nối tiếp với tụ điện có điện dung$\dfrac{{{10}^{-4}}}{\pi }$F. Tại thời điểm t điện áp tức thời giữa hai đầu đoạn mạch là u = 200V. Giá trị điện áp tức thời hai đầu tụ điện ở thời điểm t?
[A]. 400 V.
[B]. 100 V.
[C]. 200 V.
[D]. -100 V.
Luôn có: $\dfrac{{{u}_{L}}}{{{u}_{C}}}=-\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=-\dfrac{1}{2}\to {{u}_{C}}=-2{{u}_{L}}$
Mà tại thời điểm t: u = uL + uC = 200 V → uL = -200 V và uC = 400 V.