Chuyên đề cực trị RLC điện xoay chiều có tần số thay đổi, vật lí lớp 12
Câu 1.
Đặt điện áp xoay chiều u = U0cos2\[\pi \]ft, có U0 không đổi và f thay đổi được vào hai đầu một tụ điện. Khi f = 50 Hz thì cường độ dòng điện hiệu dụng qua tụ điện là 1 A. Để cường độ dòng điện hiệu dụng qua tụ là 4 A thì tần số dòng điện là
[A]. 400 Hz.
[B]. 200 Hz.
[C]. 100 Hz.
[D]. 50 Hz.
Ta có. $\left\{ \begin{matrix} {{I}_{1}}=\dfrac{{{U}_{C}}}{{{Z}_{1C}}}={{U}_{C}}. {{\omega }_{1}}C \\ {{I}_{2}}=\dfrac{{{U}_{C}}}{{{Z}_{2C}}}={{U}_{C}}. {{\omega }_{2}}C \\ \end{matrix} \right. \Rightarrow \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{\omega }_{1}}}{{{\omega }_{2}}}=\dfrac{{{f}_{1}}}{{{f}_{2}}}\Rightarrow \dfrac{1}{4}=\dfrac{50}{{{f}_{2}}}\Rightarrow {{f}_{2}}=200\left( Hz \right)$
Câu 2.
Đặt điện áp xoay chiều$u=200\sqrt{2}\cos 2\pi ft$ (V), f thay đổi được vào hai đầu đoạn mạch có R = 50 Ω, cuộn cảm thuần \[L=\dfrac{2}{\pi }H\]và tụ điện \[C=\dfrac{{{2. 10}^{-4}}}{\pi }F\]mắc nối tiếp. Khi điều chỉnh tần số f để cường độ dòng điện hiệu dụng qua đoạn mạch bằng 4 A thì giá trị của f là
[A]. 100 Hz.
[B]. 25 Hz.
[C]. 50 Hz.
[D]. 40 Hz.
Ta có. $Z=\dfrac{U}{I}=\dfrac{200}{4}=50\left( \Omega \right)$ Mặt khác, ta có. ${{Z}^{2}}={{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{50}^{2}}\Leftrightarrow |{{Z}_{L}}-{{Z}_{C}}|=0\Rightarrow \left[ \begin{array}{l} {{Z}_{L}}={{Z}_{C}} \\ {{Z}_{L}}=-{{Z}_{C}} \end{array} \right. \Leftrightarrow \omega =\dfrac{1}{\sqrt{LC}}=50\pi \left( rad/s \right)$ $\Rightarrow \omega =2\pi f=50\left( rad/s \right)\Rightarrow f=25\left( Hz \right)$
Câu 3. CĐ-2009
CĐ-2009). Đặt điện áp xoay chiều u = U0cos2\[\pi \]ft, có U0 không đổi và f thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi f = f0 thì trong đoạn mạch có cộng hưởng điện. Giá trị của f0 là
[A]. $\dfrac{2}{\sqrt{LC}}$.
[B]. $\dfrac{2\pi }{\sqrt{LC}}$.
[C]. $\dfrac{1}{\sqrt{LC}}$.
[D]. $\dfrac{1}{2\pi \sqrt{LC}}$.
Khi f = f0 thì trong đoạn mạch có cộng hưởng điện $\Leftrightarrow {{Z}_{L}}={{Z}_{C}}\Leftrightarrow L{{\omega }_{0}}=\dfrac{1}{C{{\omega }_{0}}}\Rightarrow {{\omega }_{0}}=\dfrac{1}{\sqrt{LC}}=2\pi {{f}_{0}}0\Rightarrow {{f}_{0}}=\dfrac{1}{2\pi \sqrt{LC}}$
Câu 4.
Đặt điện áp xoay chiều$u=U\sqrt{2}\cos 2\pi ft$, có U không đổi và f thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi f = f0 thì điện áp hiệu dụng giữa hai đầu điện trở UR = U. Tần số f0 nhận giá trị là
[A]. \[\dfrac{1}{\sqrt{LC}}. \]
[B]. \[\dfrac{1}{2\pi \sqrt{LC}}. \]
[C]. \[2\pi \sqrt{LC}. \]
[D]. \[\dfrac{1}{2\pi LC}. \]
Khi f = f0 thì điện áp hiệu dụng giữa hai đầu điện trở UR = U $\Rightarrow R=Z\Rightarrow {{Z}_{L}}={{Z}_{C}}$$\Rightarrow $ Mạch xảy ra cộng hưởng điện $\Leftrightarrow {{Z}_{L}}={{Z}_{C}}\Leftrightarrow L{{\omega }_{0}}=\dfrac{1}{C{{\omega }_{0}}}\Rightarrow {{\omega }_{0}}=\dfrac{1}{\sqrt{LC}}=2\pi {{f}_{0}}0\Rightarrow {{f}_{0}}=\dfrac{1}{2\pi \sqrt{LC}}$
Câu 5.
Đặt điện áp xoay chiều$u=U\sqrt{2}\cos \omega t$, có U không đổi và ω thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi ω = ω0 thì công suất đạt cực đại Pmax. Khi đó Pmax được xác định bởi biểu thức
[A]. \[{{P}_{\max }}=\dfrac{{{U}^{2}}}{R}. \]
[B]. \[{{P}_{\max }}=I_{o}^{2}. R. \]
[C]. \[{{P}_{\max }}=\dfrac{{{U}^{2}}}{{{R}^{2}}}. \]
[D]. \[{{P}_{\max }}=\dfrac{{{U}^{2}}}{2R}. \]
Khi ω = ω0 thì công suất đạt cực đại ${{P}_{max}}$ $\Rightarrow $ Mạch xảy ra cộng hưởng điện$\Rightarrow {{P}_{max}}=\dfrac{{{U}^{2}}}{R}$
Câu 6. CĐ-2012
Đặt điện áp u = U0cos(\[\omega \]t + \[\pi \]) (U0 không đổi, w thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Điều chỉnh \[\omega \] = \[\omega_1\] thì cảm kháng của cuộn cảm thuần bằng 4 lần dung kháng của tụ điện. Khi \[\omega \] = \[\omega_2\] thì trong mạch xảy ra hiện tượng cộng hưởng điện. Hệ thức đúng là
[A].ω1 = 2ω2.
[B].ω2 = 2ω1.
[C].ω1 = 4ω2.
[D].ω2 = 4ω1.
Điều chỉnh w = w1 thì cảm kháng của cuộn cảm thuần bằng 4 lần dung kháng của tụ điện $\Rightarrow {{Z}_{L}}=4{{Z}_{C}}\Rightarrow L{{\omega }_{1}}=\dfrac{4}{C{{\omega }_{1}}}\Rightarrow \omega _{1}^{2}=\dfrac{4}{LC}\Rightarrow {{\omega }_{1}}=\dfrac{2}{\sqrt{LC}}$(1) Khi w = w2 thì trong mạch xảy ra hiện tượng cộng hưởng điện $\Rightarrow {{Z}_{L}}={{Z}_{C}}\Leftrightarrow L{{\omega }_{2}}=\dfrac{1}{C{{\omega }_{2}}}\Rightarrow {{\omega }_{2}}=\dfrac{1}{\sqrt{LC}}$ (2) Lấy $\dfrac{\left( 1 \right)}{\left( 2 \right)}=\dfrac{{{\omega }_{1}}}{{{\omega }_{2}}}=\dfrac{\dfrac{2}{\sqrt{LC}}}{\dfrac{1}{\sqrt{LC}}}=2\Rightarrow {{\omega }_{1}}=2{{\omega }_{2}}$
Câu 7. ĐH-2011
Đặt điện áp u = $U\sqrt{2}\cos 2\pi ft$ (U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi tần số là f1 thì cảm kháng và dung kháng của đoạn mạch có giá trị lần lượt là 6 \[\Omega \] và 8 \[\Omega \]. Khi tần số là f2 thì hệ số công suất của đoạn mạch bằng 1. Hệ thức liên hệ giữa f1 và f2 là\[\]
[A]. f2 = $\dfrac{2}{\sqrt{3}}{{f}_{1}}. $
[B]. f2 = $\dfrac{\sqrt{3}}{2}{{f}_{1}}. $
[C]. f2 = $\dfrac{3}{4}{{f}_{1}}. $
[D]. f2 = $\dfrac{4}{3}{{f}_{1}}. $
Khi tần số ${{f}_{1}}$ ta có. \[\dfrac{{{Z}_{{{L}_{1}}}}}{{{Z}_{{{C}_{1}}}}}=\omega _{1}^{2}LC=\dfrac{6}{8}\Rightarrow \sqrt{LC}=\dfrac{\sqrt{3}}{2}\dfrac{1}{2\pi {{f}_{1}}}\] Khi tần số ${{f}_{2}}: $\[{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{2}}}}\Leftrightarrow {{\omega }_{2}}=\dfrac{1}{\sqrt{LC}}\Rightarrow {{f}_{2}}=\dfrac{1}{2\pi \sqrt{LC}}=\dfrac{2}{\sqrt{3}}{{f}_{1}}\]
Câu 8. ĐH–2009
Đặt điện áp xoay chiều u = Uocosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Thay đổi ω thì cường độ dòng điện hiệu dụng trong mạch khi ω = ω1 bằng cường độ dòng điện hiệu dụng trong mạch khi ω = ω2. Chọn hệ thức đúng trong các hệ thức cho dưới đây?
[A]. ${{\omega }_{1}}+{{\omega }_{2}}=\dfrac{2}{\sqrt{LC}}. $
[B]. ${{\omega }_{1}}. {{\omega }_{2}}=\dfrac{1}{LC}. $
[C]. ${{\omega }_{1}}+{{\omega }_{2}}=\dfrac{2}{LC}. $
[D]. \[{{\omega }_{1}}. {{\omega }_{2}}=\dfrac{1}{\sqrt{LC}}. \]
Thay đổi ω thì cường độ dòng điện hiệu dụng trong mạch khi ω = ω1 bằng cường độ dòng điện hiệu dụng trong mạch khi ω = ω2 ${{I}_{1}}={{I}_{2}}\Rightarrow \dfrac{U}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{U}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$ $\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$
Câu 9.
Đặt điện áp xoay chiều u = Uocosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi\[\omega ={{\omega }_{1}}=100\sqrt{2}\pi \] (rad/s) thì công suất tiêu thụ của đoạn mạch cực đại. Khi\[\omega ={{\omega }_{2}}\]thì cảm kháng của cuộn cảm bằng 15 \[\Omega \] và dung kháng của tụ bằng 30 \[\Omega \]. Độ tự cảm L có giá trị
[A]. \[\dfrac{0,45}{\pi }H\]
[B]. \[\dfrac{0,60}{\pi }H\]
[C]. \[\dfrac{0,15}{\pi }H\]
[D]. \[\dfrac{0,30}{\pi }H\]
Khi \[\omega ={{\omega }_{2}}\]thì cảm kháng của cuộn cảm bằng 15 W và dung kháng của tụ bằng 30 W Ta có. \[\dfrac{{{Z}_{{{L}_{2}}}}}{{{Z}_{{{C}_{2}}}}}=\omega _{2}^{2}LC=\dfrac{1}{2}\Rightarrow \sqrt{LC}=\dfrac{1}{\sqrt{2}{{\omega }_{2}}}\] Khi\[\omega ={{\omega }_{1}}=100\sqrt{2}\pi \] (rad/s) thì công suất tiêu thụ của đoạn mạch cực đại thì ${{Z}_{{{L}_{1}}}}={{Z}_{{{C}_{1}}}}\Leftrightarrow L{{\omega }_{1}}=\dfrac{1}{C{{\omega }_{1}}}\Rightarrow {{\omega }_{1}}=\dfrac{1}{\sqrt{LC}}=\sqrt{2}{{\omega }_{2}}\Rightarrow {{\omega }_{2}}=100\left( rad/s \right)$ $\Rightarrow {{Z}_{L}}=L\omega =15\left( \Omega \right)\Rightarrow L=\dfrac{{{Z}_{L}}}{\omega }=\dfrac{15}{100\pi }=\dfrac{0,15}{\pi }\left( H \right)$
Câu 10.
Đặt điện áp xoay chiều u = Uocos2πft (U0 không đổi và f thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi f = f1 thì mạch có cảm kháng là 36 Ω và dung kháng là 144 Ω. Khi f = f2 = 120 Hz thì cường độ dòng điện cùng pha với điện áp ở hai đầu đoạn mạch. Giá trị của tần số f1 là
[A]. 50 Hz.
[B]. 60 Hz.
[C]. 85 Hz.
[D]. 100 Hz.
Khi tần số ${{f}_{1}}$ ta có. \[\dfrac{{{Z}_{{{L}_{1}}}}}{{{Z}_{{{C}_{1}}}}}=\omega _{1}^{2}LC=\dfrac{1}{4}\Rightarrow {{\omega }_{1}}=\dfrac{1}{2}\dfrac{1}{\sqrt{LC}}\](1) Khi tần số ${{f}_{2}}: $\[{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{2}}}}\Leftrightarrow L{{\omega }_{2}}=\dfrac{1}{C{{\omega }_{2}}}\Rightarrow {{\omega }_{2}}=\dfrac{1}{\sqrt{LC}}\] (2) Lấy $\dfrac{\left( 1 \right)}{\left( 2 \right)}\Rightarrow \dfrac{{{\omega }_{1}}}{{{\omega }_{2}}}=\dfrac{1}{2}\Rightarrow {{\omega }_{2}}=2{{\omega }_{1}}\Rightarrow {{f}_{2}}=2{{f}_{1}}\Rightarrow {{f}_{1}}=60\left( Hz \right)$
Câu 11.
Một đoạn mạch RLC không phân nhánh mắc vào nguồn điện xoay chiều có điện áp hiệu dụng không đổi, tần số thay đổi được. Khi điều chỉnh tần số, người ta thấy rằng với tần số bằng 16 Hz và 36 Hz thì công suất tiêu thụ trên mạch như nhau. Để mạch xảy ra cộng hưởng điện thì phải điều chỉnh tần số bằng
[A]. 24 Hz.
[B]. 26 Hz.
[C]. 52 Hz.
[D]. 20 Hz.
Khi điều chỉnh tần số, người ta thấy rằng với tần số bằng 16 Hz và 36 Hz thì công suất tiêu thụ trên mạch như nhau. ${{P}_{1}}={{P}_{2}}\Leftrightarrow cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$ $\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$ Để mạch sảy ra cộng hưởng $\Leftrightarrow {{Z}_{{{L}_{0}}}}={{Z}_{{{C}_{0}}}}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}\Rightarrow f_{0}^{2}={{f}_{1}}. {{f}_{2}}$ Thay số vào ra được. ${{f}_{0}}=\sqrt{{{f}_{1}}. {{f}_{2}}}=\sqrt{16. 36}=24\left( Hz \right)$
Câu 12.
Đặt điện áp xoay chiều$u=100\sqrt{2}\cos \omega t$ (V), ω thay đổi được vào hai đầu đoạn mạch có R = 50 Ω, cuộn cảm thuần \[L=\dfrac{1}{\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-4}}}{\pi }F\]mắc nối tiếp. Khi ω = ω1 = 200π rad/s thì công suất mạch tiêu thụ là 32 W. Thấy rằng công suất mạch tiêu thụ vẫn là 32 W với tần số góc là ω = ω2 và bằng
[A]. 100π rad/s.
[B]. 50π rad/s.
[C]. 300π rad/s.
[D]. 150π rad/s.
Theo bài ra, ta có. ${{P}_{1}}={{P}_{2}}\Leftrightarrow cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$ $\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$ Thay số vào, ta được. $\dfrac{1}{\dfrac{1}{\pi }. \dfrac{{{10}^{-4}}}{\pi }}=200\pi . {{\omega }_{2}}\Rightarrow {{\omega }_{2}}=50\pi \left( rad/s \right)$
Câu 13.
Một mạch điện RLC nối tiếp, cuộn dây thuần cảm được mắc vào một điện áp xoay chiều u = U0cos2πft (U0 không đổi và f thay đổi được). Khi \[f={{f}_{1}}=36\text{ }Hz\]và \[f={{f}_{2}}=64\text{ }Hz\]thì công suất tiêu thụ của mạch bằng nhau P1 = P2. Khi \[f={{f}_{3}}=48\text{ }Hz\]công suất tiêu thụ của mạch bằng P3 khi \[f={{f}_{4}}=50\text{ }Hz\]công suất tiêu thụ của mạch bằng P4. So sánh các công suất ta có.
[A]. \[{{P}_{4}}<{{P}_{2}}. \]
[B]. \[{{P}_{4}}<{{P}_{3}}. \]
[C]. \[{{P}_{4}}>{{P}_{3}}. \]
[D]. \[{{P}_{3}}<{{P}_{1}}. \]
Khi \[f={{f}_{1}}=36\text{ }Hz\]và \[f={{f}_{2}}=64\text{ }Hz\]thì công suất tiêu thụ của mạch bằng nhau P1 = P2 Theo bài ra, ta có${{P}_{1}}={{P}_{2}}\Leftrightarrow cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$ $\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}\Rightarrow {{\omega }_{0}}={{\omega }_{1}}. {{\omega }_{2}}$ Hay ${{f}_{0}}={{f}_{1}}. {{f}_{2}}$ Xét ${{f}_{3}}=48\left( Hz \right)\Rightarrow {{f}_{0}}={{f}_{3}}=\sqrt{{{f}_{1}}. {{f}_{2}}}=48\left( Hz \right)\Rightarrow $ Mạch xảy ra cộng hưởng $\Rightarrow $ Công suất tiêu thụ của đoạn mạch lớn nhất nên ${{P}_{3}}={{P}_{max}}\Rightarrow {{P}_{3}}>{{P}_{4}}$
Câu 14.
Đặt điện áp xoay chiều $u=200\sqrt{2}\cos \omega t$ (f thay đổi được) vào hai đầu đoạn mạch có R = 80 Ω, cuộn dây có L = 0,318 H và điện trở trong r = 20 Ω, tụ điện có C = 15,9 µF mắc nối tiếp. Điều chỉnh f để công suất trên toàn mạch đạt giá trị cực đại, khi đó giá trị của f và P lần lượt là
[A]. f = 70,78 Hz và P = 400 W.
[B]. f = 70,78 Hz và P = 500 W.
[C]. f = 444,7 Hz và P = 2000 W.
[D]. f = 31,48 Hz và P = 400 W.
Điều chỉnh f để công suất trên toàn mạch đạt giá trị cực đại $\Rightarrow $ Mạch xảy ra cộng hưởng Hay ${{Z}_{L}}={{Z}_{C}}\Leftrightarrow \omega =\dfrac{1}{\sqrt{LC}}=444,72\left( rad/s \right)\Rightarrow f=\dfrac{\omega }{2\pi }=70,78\left( Hz \right)$ Và ${{P}_{max}}=\dfrac{{{U}^{2}}}{R+r}=\dfrac{{{200}^{2}}}{100}=400\left( \text{W} \right)$
Câu 15.
Đặt điện áp xoay chiều u = Uocos2πft (U0 không đổi và f thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi tần số dòng điện là fo = 50 Hz thì công suất tiêu thụ trên mạch là lớn nhất. Khi tần số dòng điện là f1 hoặc f2 thì mạch tiêu thụ cùng công suất là P. Biết rằng f1 + f2 = 145 Hz (với f1 < f2), tần số f1, f2 có giá trị lần lượt là
[A]. f1 = 45 Hz; f2 = 100 Hz.
[B]. f1 = 25 Hz; f2 = 120 Hz.
[C]. f1 = 50 Hz; f2 = 95 Hz.
[D]. f1 = 20 Hz; f2 = 125 Hz.
Khi điều chỉnh tần số, người ta thấy rằng với tần số bằng 16 Hz và 36 Hz thì công suất tiêu thụ trên mạch như nhau. ${{P}_{1}}={{P}_{2}}\Leftrightarrow cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$ $\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$ Để mạch sảy ra cộng hưởng $\Leftrightarrow {{Z}_{{{L}_{0}}}}={{Z}_{{{C}_{0}}}}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}\Rightarrow f_{0}^{2}={{f}_{1}}. {{f}_{2}}={{50}^{2}}$(1) Và ${{f}_{1}}+{{f}_{2}}=145\left( Hz \right)\Rightarrow {{f}_{1}}=145-{{f}_{2}}$ (2) thế vào (1), ta được. ${{f}_{1}}\left( 145-{{f}_{1}} \right)={{50}^{2}}\Leftrightarrow f_{1}^{2}-145{{f}_{1}}+2500=0\Rightarrow \left[ \begin{array}{l} {{f}_{1}}=125\left( Hz \right) \\ {{f}_{1}}=20\left( Hz \right) \end{array} \right. \Rightarrow \left[ \begin{array}{l} {{f}_{2}}=20\left( Hz \right)(l)\left( {{f}_{2}}>{{f}_{1}} \right) \\ {{f}_{2}}=125\left( Hz \right) \end{array} \right. $
Câu 16.
Đoạn mạch xoay chiều RLC, cuộn dây thuần cảm, biết L = CR2. Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định, với tần số góc \[\omega \] thay đổi, trong mạch có cùng hệ số công suất với hai tần số là \[\omega \]1 = 50\[\pi \] rad/s và \[\omega \]2 = 200\[\pi \] rad/s. Hệ số công suất của mạch là
[A]. $\dfrac{8}{17}$
[B]. $\dfrac{2}{\sqrt{13}}$
[C]. $\dfrac{3}{\sqrt{11}}$
[D]. $\dfrac{5}{\sqrt{57}}$
Áp dụng công thức. \[c\text{os}\varphi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{{{R}^{2}}+{{(\omega L-\dfrac{1}{\omega C})}^{2}}}}\] Do \[cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\] ta có. ${{\left( {{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C} \right)}^{2}}={{\left( {{\omega }_{2}}L-\dfrac{1}{{{\omega }_{2}}C} \right)}^{2}}$ mà \[{{\omega }_{1}}\ne {{\omega }_{2}}\] nên ${{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C}=-\left( {{\omega }_{2}}L-\dfrac{1}{{{\omega }_{2}}C} \right)\Rightarrow \left( {{\omega }_{1}}+{{\omega }_{2}} \right)L=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{2}}}+\dfrac{1}{{{\omega }_{2}}} \right)$ \[\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}\] (1) Theo bài ra L = CR2 (2) Từ (1) và (2) ta có. $\left\{ \begin{array}{l} L=\dfrac{R}{\sqrt{{{\omega }_{1}}{{\omega }_{2}}}}=\dfrac{R}{100\pi } \\ C=\dfrac{1}{R\sqrt{{{\omega }_{1}}{{\omega }_{2}}}}=\dfrac{1}{100\pi R} \end{array} \right. $ \[\Rightarrow c\text{os}\varphi =\dfrac{R}{{{Z}_{1}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{({{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C})}^{2}}}}=\dfrac{2}{\sqrt{13}}\]
Câu 17.
Mạch điện xoay chiều R, L, C mắc nối tiếp. Điện áp ở hai đầu đoạn mạch là $u={{U}_{0}}\cos \omega t$. Chỉ có ω thay đổi được. Điều chỉnh ω thấy khi giá trị của nó là ω1 hoặc ω2 (ω2 < ω1) thì dòng điện hiệu dụng đều nhỏ hơn cường độ hiệu dụng cực đại có thể đạt được n lần (n > 1). Biểu thức tính R là
[A]. \[R=\dfrac{(\omega {}_{1}-{{\omega }_{2}})}{L\sqrt{{{n}^{2}}-1}}\]
[B]. \[R=\dfrac{L({{\omega }_{1}}-{{\omega }_{2}})}{\sqrt{{{n}^{2}}-1}}\]
[C]. \[R=\dfrac{L({{\omega }_{1}}-{{\omega }_{2}})}{{{n}^{2}}-1}\].
[D]. \[R=\dfrac{L{{\omega }_{1}}{{\omega }_{2}}}{\sqrt{{{n}^{2}}-1}}\]
Ta có. \[{{I}_{1}}=\dfrac{U}{\sqrt{{{R}^{2}}+{{\left( {{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C} \right)}^{2}}}};{{I}_{2}}=\dfrac{U}{\sqrt{{{R}^{2}}+{{\left( {{\omega }_{2}}L-\dfrac{1}{{{\omega }_{2}}C} \right)}^{2}}}}\] \[{{I}_{1}}={{I}_{2}}\Rightarrow {{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C}=-\left( {{\omega }_{2}}L-\dfrac{1}{{{\omega }_{2}}C} \right)\] hay \[\left( {{\omega }_{1}}+{{\omega }_{2}} \right)L=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow LC=\dfrac{1}{{{\omega }_{1}}{{\omega }_{2}}}\Rightarrow C{{\omega }_{1}}=\dfrac{1}{L{{\omega }_{2}}}\](*) Khi \[I={{I}_{cd}}=\dfrac{U}{R}\Rightarrow {{I}_{1}}={{I}_{2}}=\dfrac{{{I}_{cd}}}{n}=\dfrac{U}{nR}\Rightarrow {{R}^{2}}+{{\left( {{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C} \right)}^{2}}={{n}^{2}}{{R}^{2}}\] \[\Rightarrow {{\left( {{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C} \right)}^{2}}=\left( {{n}^{2}}-1 \right){{R}^{2}}\] (**) Từ (*) và (**) ta có. \[\left( {{n}^{2}}-1 \right){{R}^{2}}={{\left( {{\omega }_{1}}L-{{\omega }_{2}}L \right)}^{2}}={{L}^{2}}{{\left( {{\omega }_{1}}-{{\omega }_{2}} \right)}^{2}}\] Do đó. \[R=\dfrac{L\left( {{\omega }_{1}}-{{\omega }_{2}} \right)}{\sqrt{{{n}^{2}}-1}}\]
Câu 18. ĐH-2012
Đặt điện áp u = U0cosωt (V) (U0 không đổi, ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm $\dfrac{4}{5\pi }H$ và tụ điện mắc nối tiếp. Khi ω = ω0 thì cường độ dòng điện hiệu dụng qua đoạn mạch đạt giá trị cực đại Im. Khi ω = ω1 hoặc ω = ω2 thì cường độ dòng điện cực đại qua đoạn mạch bằng nhau và bằng IM. Biết ω1 – ω2 = 200π (rad/s). Giá trị của R bằng
[A]. 160 Ω.
[B]. 200 Ω.
[C]. 50 Ω.
[D]. 150 Ω.
+ Từ \[{{I}_{1}}={{I}_{2}}\Rightarrow \left( {{Z}_{1L}}-{{Z}_{1C}} \right)=-\left( {{Z}_{2L}}-{{Z}_{2C}} \right)\] + Từ \[{{I}_{01}}=\text{ }{{I}_{m}}\Rightarrow {{I}_{1}}=\dfrac{{{I}_{m}}}{\sqrt{2}}\Leftrightarrow {{Z}_{1}}=\sqrt{2}{{Z}_{m}}\Leftrightarrow \sqrt{{{R}^{2}}+\left( {{Z}_{1L}}-{{Z}_{1C}} \right)}=\sqrt{2}R\] $\Rightarrow {{Z}_{1L}}-{{Z}_{1C}}=R\Rightarrow {{Z}_{2L}}-{{Z}_{2C}}=-R\Rightarrow tan{{\varphi }_{1}}=-tan{{\varphi }_{2}}=1\Rightarrow {{\varphi }_{1}}=-{{\varphi }_{2}}=\dfrac{\pi }{4}$ $\Rightarrow \left\{ \begin{matrix} \dfrac{{{\omega }_{1}}L-\dfrac{1}{{{\omega }_{1}}C}}{R}=1 \\ \dfrac{{{\omega }_{2}}L-\dfrac{1}{{{\omega }_{2}}C}}{R}=-1 \\ \end{matrix} \right. $ (1) Mặt khác ta đã quen thuộc ${{\omega }_{1}}{{\omega }_{2}}=\omega _{0}^{2}=\dfrac{1}{LC}(2)$ Từ (1) và (2) $\Rightarrow L=\dfrac{R}{{{\omega }_{1}}-{{\omega }_{2}}}\to R=({{\omega }_{1}}-{{\omega }_{2}})L=200\pi . \dfrac{4}{5\pi }=160\Omega $
Câu 19.
Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có tần số f thay đổi được. Khi f = f1 thì hệ số công suất cosφ1 = 1; khi f = 2f1 thì hệ số công suất là cosφ2 = 0,707. Khi f = 1,5f1 thì hệ số công suất cosφ3 là
[A]. 0,625.
[B]. 0,874.
[C]. 0,486.
[D]. 0,546.
Khi \[f={{f}_{1}}\], hệ số công suất \[cos\varphi =1\Rightarrow \] Mạch xảy ra cộng hưởng điện \[\Rightarrow {{Z}_{{{L}_{1}}}}={{Z}_{{{C}_{1}}}}\] Khi \[f=2{{f}_{1}}\Rightarrow \left\{ \begin{array}{l} {{Z}_{{{L}_{2}}}}=2{{Z}_{{{L}_{1}}}} \\ {{Z}_{{{C}_{2}}}}=\dfrac{{{Z}_{{{C}_{1}}}}}{2}=\dfrac{{{Z}_{{{L}_{1}}}}}{2} \end{array} \right. \] \[\Rightarrow cos{{\varphi }_{2}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}^{2}}}}=\dfrac{1}{\sqrt{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+{{\left( 2{{Z}_{{{L}_{1}}}}-\dfrac{{{Z}_{{{L}_{1}}}}}{2} \right)}^{2}}}}=\dfrac{1}{\sqrt{2}}\Rightarrow R=\dfrac{3}{2}{{Z}_{{{L}_{1}}}}\] Khi \[f=1,5{{f}_{1}}\Rightarrow \left\{ \begin{array}{l} {{Z}_{{{L}_{3}}}}=1,5{{Z}_{{{L}_{1}}}} \\ {{Z}_{{{C}_{3}}}}=\dfrac{2. {{Z}_{{{C}_{1}}}}}{3}=\dfrac{2. {{Z}_{{{L}_{1}}}}}{2} \end{array} \right. \] \[\Rightarrow cos{{\varphi }_{3}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{{{L}_{3}}}}-{{Z}_{{{C}_{3}}}} \right)}^{2}}}}=\dfrac{\dfrac{3}{2}{{Z}_{{{L}_{1}}}}}{\sqrt{\dfrac{9}{4}Z_{{{C}_{1}}}^{2}+{{\left( 1,5{{Z}_{{{L}_{1}}}}-\dfrac{2}{3}{{Z}_{{{L}_{1}}}} \right)}^{2}}}}\approx 0,874\]
Câu 20.
Đặt vào hai đầu đoạn mạch RC nối tiếp một điện áp xoay chiều có tần số f thay đổi được. Khi tần số là \[{{f}_{1}}\] hoặc \[{{f}_{2}}=3{{f}_{1}}\] thì hệ số công suất tương ứng của đoạn mạch là cosφ1 và cosφ2 với \[\cos {{\varphi }_{2}}=\sqrt{2}\cos {{\varphi }_{1}}. \] Khi tần số là \[{{f}_{3}}=\dfrac{{{f}_{1}}}{\sqrt{2}}\] hệ số công suất của đoạn mạch cosφ3 bằng
[A]. \[\dfrac{\sqrt{7}}{4}\]
[B]. \[\dfrac{\sqrt{7}}{5}\]
[C]. \[\dfrac{\sqrt{5}}{4}\]
[D]. \[\dfrac{\sqrt{5}}{5}\]
Ta có. ${{f}_{2}}=3{{f}_{1}}\Rightarrow {{\omega }_{2}}=3{{\omega }_{1}}\Rightarrow {{Z}_{{{C}_{1}}}}=3{{Z}_{{{C}_{2}}}}$ Mặt khác. \[\cos {{\varphi }_{2}}=\sqrt{2}\cos {{\varphi }_{1}}\Leftrightarrow co{{s}^{2}}{{\varphi }_{2}}=2co{{s}^{2}}{{\varphi }_{1}}\Leftrightarrow \dfrac{1}{co{{s}^{2}}{{\varphi }_{2}}}=\dfrac{1}{2}. \dfrac{1}{co{{s}^{2}}{{\varphi }_{1}}}\] \[\Rightarrow 1+ta{{n}^{2}}{{\varphi }_{2}}=\dfrac{1}{2}\left( 1+ta{{n}^{2}}{{\varphi }_{1}} \right)\Leftrightarrow 1+\dfrac{Z_{{{C}_{2}}}^{2}}{{{R}^{2}}}=\dfrac{1}{2}\left( 1+\dfrac{Z_{{{C}_{1}}}^{2}}{{{R}^{2}}} \right)=\dfrac{1}{2}\left( 1+\dfrac{9Z_{{{C}_{2}}}^{2}}{{{R}^{2}}} \right)\] \[\Rightarrow 0,5=3,5. \dfrac{Z_{{{C}_{2}}}^{2}}{{{R}^{2}}}\Rightarrow \dfrac{Z_{{{C}_{2}}}^{2}}{{{R}^{2}}}=\dfrac{1}{7}\] \[\Rightarrow \left\{ \begin{matrix} |ta. n{{\varphi }_{2}}|=\dfrac{\sqrt{7}}{7} \\ |tan{{\varphi }_{1}}|=\dfrac{3\sqrt{7}}{7} \\ \end{matrix} \right. \Rightarrow \left\{ \begin{matrix} cos{{\varphi }_{2}}=\dfrac{\sqrt{14}}{4} \\ cos{{\varphi }_{1}}=\dfrac{\sqrt{7}}{4} \\ \end{matrix} \right. \] Lại có. \[{{f}_{3}}=\dfrac{{{f}_{1}}}{\sqrt{2}}\Rightarrow {{\omega }_{3}}=\dfrac{{{\omega }_{1}}}{\sqrt{2}}\Rightarrow {{Z}_{{{C}_{1}}}}=\dfrac{{{Z}_{{{C}_{3}}}}}{\sqrt{2}}\] \[\dfrac{tan{{\varphi }_{3}}}{tan{{\varphi }_{1}}}=\dfrac{\dfrac{{{Z}_{{{C}_{3}}}}}{R}}{\dfrac{{{Z}_{{{C}_{1}}}}}{R}}=\dfrac{{{Z}_{{{C}_{3}}}}}{{{Z}_{{{C}_{1}}}}}=\sqrt{2}\Rightarrow tan{{\varphi }_{3}}=\sqrt{2}tan{{\varphi }_{1}}=\dfrac{3\sqrt{14}}{7}\]\[\Rightarrow cos{{\varphi }_{3}}=\dfrac{\sqrt{7}}{5}\]
Câu 21.
Đặt điện áp xoay chiều$u=100\sqrt{2}\cos \omega t$ (V), ω thay đổi được vào hai đầu đoạn mạch có R = \[50\sqrt{2}\]Ω, cuộn cảm thuần \[L=\dfrac{1}{\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-4}}}{\pi }F\]mắc nối tiếp. Thay đổi ω thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại ULmax. Giá trị của ULmaxlà
[A]. $\dfrac{100}{\sqrt{7}}$V
[B]. $\dfrac{600}{\sqrt{7}}$V
[C]. $\dfrac{200}{\sqrt{7}}$V
[D]. $\dfrac{400}{\sqrt{7}}$V
Thay đổi ω thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại \[{{U}_{Lmax}}\] thì \[{{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}\] Thay số vào ta được. \[{{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}=\dfrac{2. 100. \dfrac{1}{\pi }}{50\sqrt{2}\sqrt{4. \dfrac{1}{\pi }. \dfrac{{{10}^{-4}}}{\pi }-{{\left( 50\sqrt{2} \right)}^{2}}. {{\left( \dfrac{{{10}^{-4}}}{\pi } \right)}^{2}}}}=\dfrac{400}{\sqrt{7}}\left( V \right)\]
Câu 22.
Đặt điện áp xoay chiều u = U0cos\[\omega \]t (U0 không đổi và \[\omega \] thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Thay đổi ω đến giá trị mà điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại là ULmax; khi đó, cảm kháng và dung kháng của mạch là ZL và ZC. Giá trị ULmax có biểu thức
[A]. ${{U}_{Lmax}}=\dfrac{U}{\sqrt{1-\dfrac{Z_{C}^{2}}{Z_{L}^{2}}}}$
[B]. ${{U}_{Lmax}}=\dfrac{2UL}{\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}$
[C]. ${{U}_{Lmax}}=\dfrac{U}{\sqrt{1-\dfrac{Z_{L}^{2}}{Z_{C}^{2}}}}$
[D]. ${{U}_{Lmax}}=\dfrac{2U}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}$
Thay đổi ω thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại \[{{U}_{Lmax}}\] thì \[{{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}\]
Câu 23.
Một đoạn mạch RLC nối tiếp, cuộn dây thuần cảm với CR2 < 2L. Đặt điện áp $u=U\sqrt{2}\cos \omega t$, U không đổi và ω có thể thay đổi. Điều chỉnh ω để điện áp hiệu dụng giữa hai cuộn cảm đạt cực đại là ULmax và ${{U}_{L\max }}=\dfrac{41U}{10}$. Hệ số công suất tiêu thụ của cả đoạn mạch là
[A]. 0,6
[B]. $\dfrac{1}{\sqrt{15}}$
[C]. $\dfrac{1}{\sqrt{26}}$
[D]. 0,8
Điều chỉnh ω để điện áp hiệu dụng giữa hai cuộn cảm đạt cực đại là ULmax Với $\left\{ \begin{matrix} {{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}} \\ Z_{L}^{2}={{Z}^{2}}+Z_{C}^{2} \\ \end{matrix} \right. $ Ta có. ${{U}_{L\max }}=\dfrac{41U}{10}\Rightarrow {{Z}_{L}}=\dfrac{41Z}{10}$ Giả sử. ${{Z}_{L}}=41\left( \Omega \right)\Rightarrow Z=40\left( \Omega \right)\Rightarrow {{Z}_{C}}=\sqrt{Z_{L}^{2}-{{Z}^{2}}}=\sqrt{{{41}^{2}}-{{40}^{2}}}=9\left( \Omega \right)$ $\Rightarrow R=\sqrt{2{{Z}_{C}}. \left( {{Z}_{L}}-{{Z}_{C}} \right)}=\sqrt{2. 9\left( 41-9 \right)}=24\left( \Omega \right)$ Hệ số công suất tiêu thụ của cả đoạn mạch là $cos\varphi =\dfrac{R}{Z}=\dfrac{24}{40}=0,6$
Câu 24. ĐH-2011
Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Khi ω = ω1 hoặc ω = ω2 thì điện áp hiệu dụng giữa hai bản tụ điện có cùng một giá trị. Khi ω = ω0 thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại. Hệ thức liên hệ giữa ω1, ω2 và ω0 là
[A]. \[{{\omega }_{0}}=\dfrac{1}{2}({{\omega }_{1}}+{{\omega }_{2}})\]
[B]. \[\omega _{0}^{2}=\dfrac{1}{2}(\omega _{1}^{2}+\omega _{2}^{2})\]
[C]. \[{{\omega }_{0}}=\sqrt{{{\omega }_{1}}{{\omega }_{2}}}\]
[D]. \[\dfrac{1}{\omega _{0}^{2}}=\dfrac{1}{2}(\dfrac{1}{\omega _{1}^{2}}+\dfrac{1}{\omega _{2}^{2}})\]
Ta có. ${{U}_{C}}=I. {{Z}_{C}}=\dfrac{U}{Z}. {{Z}_{C}}\Leftrightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{{{Z}^{2}}}. Z_{C}^{2}=\dfrac{{{U}^{2}}}{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}+\left( {{R}^{2}}{{C}^{2}}-2LC \right){{\omega }^{2}}+1}$ Đặt $x={{\omega }^{2}}>0;a={{L}^{2}}{{C}^{2}};b={{R}^{2}}{{C}^{2}}-2LC;y=a{{x}^{2}}+bx+1\Rightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{y}$ Ta có. $y’=2ax+b;y’=0\Leftrightarrow x={{x}_{0}}=-\dfrac{b}{2a};{{U}_{C}}$ cực đại Theo định lý Vi- ét đối với phương trình bậc hai ẩn là ${{\omega }^{2}}$, ta có. ${{x}_{1}}+{{x}_{2}}=-\dfrac{b}{a}=2{{x}_{0}}\Leftrightarrow 2\omega _{0}^{2}=\omega _{1}^{2}+\omega _{2}^{2}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)$
Câu 25.
Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Khi điều chỉnh cho ω = ω1 = 45 rad/s hoặc ω = ω2 = 60 rad/s thì điện áp hiệu dụng giữa hai bản tụ điện có cùng một giá trị. Để điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại thì tần số giá trị bằng
[A]. 8,44 Hz
[B]. 8,1 Hz
[C]. $36\sqrt{2}$Hz
[D]. 75 Hz
Ta có. ${{U}_{C}}=I. {{Z}_{C}}=\dfrac{U}{Z}. {{Z}_{C}}\Leftrightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{{{Z}^{2}}}. Z_{C}^{2}=\dfrac{{{U}^{2}}}{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}+\left( {{R}^{2}}{{C}^{2}}-2LC \right){{\omega }^{2}}+1}$
Đặt $x={{\omega }^{2}}>0;a={{L}^{2}}{{C}^{2}};b={{R}^{2}}{{C}^{2}}-2LC;y=a{{x}^{2}}+bx+1\Rightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{y}$
Ta có. $y’=2ax+b;y’=0\Leftrightarrow x={{x}_{0}}=-\dfrac{b}{2a};{{U}_{C}}$
cực đại Theo định lý Vi- ét đối với phương trình bậc hai ẩn là ${{\omega }^{2}}$, ta có. ${{x}_{1}}+{{x}_{2}}=-\dfrac{b}{a}=2{{x}_{0}}\Leftrightarrow 2\omega _{0}^{2}=\omega _{1}^{2}+\omega _{2}^{2}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)$
Thay số vào ta được. ${{\omega }_{0}}=\sqrt{\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)}=\sqrt{\dfrac{1}{2}\left( {{45}^{2}}+{{60}^{2}} \right)}=\dfrac{75}{\sqrt{2}}\left( rad/s \right)$
Và ${{\omega }_{0}}=2\pi . {{f}_{0}}=\dfrac{75}{\sqrt{2}}\left( \Omega \right)\Rightarrow {{f}_{0}}\approx 8,44\left( Hz \right)$
Câu 26.
Đặt điện áp xoay chiều$u=200\sqrt{2}\cos \omega t$ (V), ω thay đổi được vào hai đầu đoạn mạch có R = \[50\sqrt{3}\]Ω, cuộn cảm thuần \[L=\dfrac{1}{2\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-4}}}{2\pi }F\]mắc nối tiếp. Khi ω = ωC thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại. Giá trị ωC là
[A]. 50π rad/s
[B]. 80π rad/s
[C]. 158π rad/s
[D]. 100π rad/s
Khi ω = ωC thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại Áp dụng công thức. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}$
Thay số vào, ta được. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}=2\pi \sqrt{\dfrac{2. \dfrac{1}{2\pi }. \dfrac{2\pi }{{{10}^{-4}}}-{{\left( 50\sqrt{3} \right)}^{2}}}{2}}=496,73\left( \Omega \right)\approx 158\pi \left( rad/s \right)$
Câu 27.
Đặt điện áp xoay chiều $u=200\cos \omega t\text{ }\left( V \right)$ (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R =$30\sqrt{2}$Ω, cuộn cảm thuần \[L=\dfrac{2}{\pi }H\]và tụ điện \[C=\dfrac{{{4. 10}^{-4}}}{\pi }F\] mắc nối tiếp. Thay đổi ω để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại. Giá trị của điện áp hiệu dụng giữa hai đầu bản tụ điện khi đó là
[A]. 15,185 V.
[B]. 16,085 V.
[C]. 151,85 V.
[D]. 18,515 V.
Điều chỉnh ω để điện áp hiệu dụng giữa hai cuộn cảm đạt cực đại là ULmax Với $\left\{ \begin{matrix} {{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}} \\ Z_{L}^{2}={{Z}^{2}}+Z_{C}^{2} \\ \end{matrix} \right. $
Thay số vào ta được. ${{U}_{Lmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}=\dfrac{2. 100\sqrt{2}. \dfrac{2}{\pi }}{30\sqrt{2}\sqrt{4. \dfrac{2}{\pi }. \dfrac{{{4. 10}^{-4}}}{\pi }-{{\left( 30\sqrt{2} \right)}^{2}}{{\left( \dfrac{{{4. 10}^{-4}}}{\pi } \right)}^{2}}}}\approx 247,08\left( \Omega \right)$
Mặt khác, ta có. $Z_{L}^{2}={{Z}^{2}}+Z_{C}^{2}\Leftrightarrow U_{L}^{2}={{U}^{2}}+U_{C}^{2}\Rightarrow {{U}_{C}}=\sqrt{U_{L}^{2}-{{U}^{2}}}=202,60\left( V \right)$
Câu 28.
Đặt điện áp xoay chiều $u=200\cos \omega t\text{ }\left( V \right)$ (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R =$30\sqrt{2}$Ω, cuộn cảm thuần \[L=\dfrac{2}{\pi }H\]và tụ điện \[C=\dfrac{{{4. 10}^{-4}}}{\pi }F\] mắc nối tiếp. Thay đổi tần số để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại. Khi đó, công suất tiêu thụ trên mạch gần giá trị nào sau đây nhất?
[A]. 430 W
[B]. 330 W
[C]. 280 W
[D]. 410 W
Khi ω = ωC thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại Áp dụng công thức. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}$ Thay số vào, ta được. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}=\dfrac{\pi }{2}\sqrt{\dfrac{2. \dfrac{2}{\pi }. \dfrac{\pi }{{{4. 10}^{-4}}}-{{\left( 30\sqrt{2} \right)}^{2}}}{2}}\approx 100,58\left( rad/s \right)$ \[\Rightarrow {{Z}_{L}}=L\omega =64,03\left( \Omega \right);{{Z}_{C}}=\dfrac{1}{C\omega }=78,09\left( \Omega \right)\] Tổng trở. \[Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=44,70\left( \Omega \right)\] Công suất tiêu thụ trên mạch. \[P=UI. cos\varphi =100\sqrt{2}. \dfrac{100\sqrt{2}}{44,70}. \dfrac{30\sqrt{2}}{44,70}\approx 424,67\left( \text{W} \right)\] gần 430 W nhất
Câu 29.
Đặt điện áp xoay chiều $u=200\cos \omega t\text{ }\left( V \right)$ (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R =$50\sqrt{3}$Ω, cuộn cảm thuần \[L=\dfrac{1}{2\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-4}}}{2\pi }F\] mắc nối tiếp. Thay đổi tần số để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại. Khi đó, hệ số công suất của đoạn mạch là
[A]. 0,6
[B]. 0,8
[C]. 0,88
[D]. 0,7
Khi ω = ωC thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại Áp dụng công thức. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}$ Thay số vào, ta được. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}=2\pi \sqrt{\dfrac{2. \dfrac{1}{2\pi }. \dfrac{2\pi }{{{10}^{-4}}}-{{\left( 50\sqrt{3} \right)}^{2}}}{2}}\approx 496,73\left( rad/s \right)$ \[\Rightarrow {{Z}_{L}}=L\omega =79,06\left( \Omega \right);{{Z}_{C}}=\dfrac{1}{C\omega }=126,49\left( \Omega \right)\] Hệ số công suất của đoạn mạch. \[cos\varphi =\dfrac{R}{Z}=\dfrac{50\sqrt{3}}{126,49}\approx 0,88\]
Câu 30.
Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Khi$\omega ={{\omega }_{1}}=45\sqrt{2}$ rad/s hoặc $\omega ={{\omega }_{2}}=60\sqrt{2}$ rad/s thì điện áp hiệu dụng giữa hai đầu tụ điện có cùng một giá trị. Để điện áp hiệu dụng giữa hai đầu tụ điện lớn nhất thì tần số góc ω có giá trị bằng
[A]. 8,44 rad/s
[B]. 8,1 rad/s
[C]. $36\sqrt{2}$rad/s
[D]. 75 rad/s
Ta có. ${{U}_{C}}=I. {{Z}_{C}}=\dfrac{U}{Z}. {{Z}_{C}}\Leftrightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{{{Z}^{2}}}. Z_{C}^{2}=\dfrac{{{U}^{2}}}{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}+\left( {{R}^{2}}{{C}^{2}}-2LC \right){{\omega }^{2}}+1}$
Đặt $x={{\omega }^{2}}>0;a={{L}^{2}}{{C}^{2}};b={{R}^{2}}{{C}^{2}}-2LC;y=a{{x}^{2}}+bx+1\Rightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{y}$ Ta có. $y’=2ax+b;y’=0\Leftrightarrow x={{x}_{0}}=-\dfrac{b}{2a};{{U}_{C}}$
cực đại Theo định lý Vi- ét đối với phương trình bậc hai ẩn là
${{\omega }^{2}}$, ta có. ${{x}_{1}}+{{x}_{2}}=-\dfrac{b}{a}=2{{x}_{0}}\Leftrightarrow 2\omega _{0}^{2}=\omega _{1}^{2}+\omega _{2}^{2}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)$
Thay số vào ta được. ${{\omega }_{0}}=\sqrt{\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)}=\sqrt{\dfrac{1}{2}\left( {{45}^{2}}. 2+{{60}^{2}}. 2 \right)}=75\left( rad/s \right)$
Câu 31.
Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Khi ω1 = 50π (rad/s) hoặc ω2 = 200π (rad/s) thì công suất của mạch có cùng giá trị. Giá trị của ω để công suất trên mạch đạt cực đại là
[A]. 100π (rad/s).
[B]. 150π (rad/s).
[C]. 125π (rad/s).
[D]. 175π (rad/s).
Khi ω1 = 50π (rad/s) hoặc ω2 = 200π (rad/s) thì công suất của mạch có cùng giá trị ${{P}_{1}}={{P}_{2}}\Leftrightarrow cos{{\varphi }_{1}}=cos{{\varphi }_{2}}\Rightarrow \dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}}=\dfrac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}}$
$\Leftrightarrow {{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}={{Z}_{{{C}_{1}}}}+{{Z}_{{{C}_{2}}}}\Leftrightarrow L\left( {{\omega }_{1}}+{{\omega }_{2}} \right)=\dfrac{1}{C}\left( \dfrac{1}{{{\omega }_{1}}}+\dfrac{1}{{{\omega }_{2}}} \right)\Rightarrow \dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$
Để mạch sảy ra cộng hưởng $\Leftrightarrow {{Z}_{{{L}_{0}}}}={{Z}_{{{C}_{0}}}}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{LC}={{\omega }_{1}}. {{\omega }_{2}}$
Thay số vào ra được. ${{\omega }_{0}}=\sqrt{{{\omega }_{1}}. {{\omega }_{2}}}=\sqrt{50\pi . 200\pi }=100\pi \left( rad/s \right)$
Câu 32.
Cho mạch điện gồm R, L, C mắc nối tiếp. Cho R = 40 Ω, L = 1 (H) và C = 625 (μF). Đặt vào hai đầu mạch điện một điện áp xoay chiều u = 220cos(ωt) V, trong đó ω thay đổi được. Khi ω = ω0 điện áp hiệu dụng giữa hai bản tụ C đạt giá trị cực đại. Giá trị ω0 là
[A]. 35,5 rad/s.
[B]. 33,3 rad/s.
[C]. 28,3 rad/s.
[D]. 40 rad/s.
Khi ω = ωC thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại Áp dụng công thức. ${{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}$
Thay số vào, ta được. ${{\omega }_{0}}={{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}=\dfrac{1}{1}\sqrt{\dfrac{\dfrac{2. 1}{{{625. 10}^{-6}}}-{{\left( 40 \right)}^{2}}}{2}}=20\sqrt{2}\left( rad/s \right)\approx 28,3\left( rad/s \right)$
Câu 33.
Cho mạch xoay chiều không phân nhánh RLC có tần số dòng điện thay đổi được. Gọi f0, f1, f2 lần lượt là các giá trị của tần số dòng điện làm cho URmax, ULmax, UCmax. Khi đó ta có
[A]. \[\dfrac{{{f}_{1}}}{{{f}_{o}}}=\dfrac{{{f}_{o}}}{{{f}_{2}}}. \]
[B]. \[{{f}_{o}}={{f}_{1}}+{{f}_{2}}. \]
[C]. \[{{f}_{o}}=\dfrac{{{f}_{1}}}{{{f}_{2}}}. \]
[D]. \[f_{o}^{2}=\dfrac{{{f}_{1}}}{{{f}_{2}}}. \]
\[{{U}_{R}}={{U}_{Rmax}}\] khi trong mạch có cộng hưởng điện \[{{Z}_{L}}={{Z}_{C}}\Rightarrow f_{0}^{2}=\dfrac{1}{4{{\pi }^{2}}LC}\](1) \[{{U}_{C}}={{U}_{Cmax}}\] khi \[{{Z}_{{{C}_{2}}}}=\dfrac{{{R}^{2}}+Z_{L2}^{2}}{{{Z}_{L2}}}\Rightarrow {{R}^{2}}={{Z}_{{{L}_{2}}}}{{Z}_{{{C}_{2}}}}-Z_{{{L}_{2}}}^{2}\](*) \[{{U}_{L}}={{U}_{Lmax}}\] khi \[{{Z}_{{{L}_{1}}}}=\dfrac{{{R}^{2}}+Z_{{{C}_{1}}}^{2}}{{{Z}_{{{C}_{1}}}}}\Rightarrow {{R}^{2}}={{Z}_{{{L}_{1}}}}. {{Z}_{{{C}_{1}}}}-Z_{{{C}_{1}}}^{2}\](**) Từ (*) và (**) suy ra \[{{Z}_{L1}}{{Z}_{C1}}\text{ }{{Z}_{C1}}^{2}=~{{Z}_{L2}}{{Z}_{C2}}\text{ }{{Z}_{L2}}^{2}~~\] \[{{Z}_{L}}. {{Z}_{C}}=\dfrac{L}{C}\] suy ra \[{{Z}_{{{C}_{1}}}}=\text{ }{{Z}_{{{L}_{2}}}}~~\Rightarrow \dfrac{1}{2\pi {{f}_{1}}C}=2\pi {{f}_{2}}L\Rightarrow {{f}_{1}}. {{f}_{2}}=\dfrac{1}{4{{\pi }^{2}}LC}\](2) Từ (1) và (2) ta có \[f_{0}^{2}={{f}_{1}}. {{f}_{2}}\]
Câu 34.
Đặt điện áp xoay chiều $u=200\cos \omega t\text{ }\left( V \right)$ (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R =$50\sqrt{3}$Ω, cuộn cảm thuần \[L=\dfrac{1}{2\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-4}}}{2\pi }F\] mắc nối tiếp. Khi ω = ωL để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại ULmax. Giá trị của ωL là
[A]. 30π rad/s
[B]. 20π rad/s
[C]. 40π rad/s
[D]. 10π rad/s
Khi ω = ωL để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại ULmax Áp dụng công thức. \[{{\omega }_{L}}=\dfrac{1}{C}. \dfrac{1}{\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}\] Thay số vào, ta đươc. \[{{\omega }_{L}}=\dfrac{1}{C}. \dfrac{1}{\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}=\dfrac{2\pi }{{{10}^{-4}}}. \dfrac{1}{\sqrt{\dfrac{1}{2\pi }. \dfrac{2\pi }{{{10}^{-4}}}-\dfrac{{{\left( 50\sqrt{3} \right)}^{2}}}{2}}}=\dfrac{2\pi }{{{10}^{-4}}}. \dfrac{1}{25\sqrt{10}}\approx 800\left( rad/s \right)\] Không có đáp án
Câu 35.
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \omega t\text{ }\left( V \right)$ (U0 không đổi và w thay đổi được) vào hai đầu đoạn mạch gồm điện trở R =$20\sqrt{2}$Ω, cuộn cảm thuần \[L=\dfrac{4}{5\pi }H\]và tụ điện \[C=\dfrac{{{10}^{-3}}}{2\pi }F\] mắc nối tiếp. Khi ω = ω1 thì ULmax; ω = ω2 thì UCmax. Khi ω = ω1 + ω2 thì hệ số công suất của mạch bằng
[A]. 0,8
[B]. 0,58
[C]. 0,08
[D]. 0,42
Khi \[\omega ={{\omega }_{1}}\] để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại ULmax
Áp dụng công thức. \[{{\omega }_{1}}={{\omega }_{L}}=\dfrac{1}{C}. \dfrac{1}{\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}=\dfrac{2\pi }{{{10}^{-3}}}\dfrac{1}{\sqrt{\dfrac{4}{5\pi }. \dfrac{2\pi }{{{10}^{-3}}}-\dfrac{{{\left( 20\sqrt{2} \right)}^{2}}}{2}}}=181,38\left( \Omega \right)\]
Khi \[\omega ={{\omega }_{2}}\] thì điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại Áp dụng công thức. ${{\omega }_{2}}={{\omega }_{C}}=\dfrac{1}{L}\sqrt{\dfrac{\dfrac{2L}{C}-{{R}^{2}}}{2}}=\dfrac{5\pi }{4}\sqrt{\dfrac{2. \dfrac{4}{5\pi }. \dfrac{2\pi }{{{10}^{-3}}}-{{\left( 20\sqrt{2} \right)}^{2}}}{2}}\approx 136,03\left( \Omega \right)$
\[\Rightarrow \omega ={{\omega }_{1}}+{{\omega }_{2}}=317,41\left( \Omega \right)\Rightarrow {{Z}_{L}}=80,83\left( \Omega \right);{{Z}_{C}}=19,80\left( \Omega \right)\]
Tổng trở. \[Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\approx 67,27\left( \Omega \right)\]
Hệ số công suất của mạch bằng \[cos\varphi =\dfrac{R}{Z}=\dfrac{20\sqrt{2}}{67,27}\approx 0,42\]
Câu 36.
Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Khi $\omega ={{\omega }_{1}}=45$ rad/s hoặc$\omega ={{\omega }_{2}}=60$ rad/s thì điện áp hiệu dụng giữa hai đầu cuộn cảm có cùng một giá trị. Để điện áp hiệu dụng giữa hai đầu cuộn cảm lớn nhất thì tần số f bằng
[A]. 8,44 Hz
[B]. 8,1 Hz
[C]. $36\sqrt{2}$Hz
[D]. 75 Hz
Ta có. ${{U}_{C}}=I. {{Z}_{C}}=\dfrac{U}{Z}. {{Z}_{C}}\Leftrightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{{{Z}^{2}}}. Z_{C}^{2}=\dfrac{{{U}^{2}}}{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}+\left( {{R}^{2}}{{C}^{2}}-2LC \right){{\omega }^{2}}+1}$
Đặt $x={{\omega }^{2}}>0;a={{L}^{2}}{{C}^{2}};b={{R}^{2}}{{C}^{2}}-2LC;y=a{{x}^{2}}+bx+1\Rightarrow U_{C}^{2}=\dfrac{{{U}^{2}}}{y}$
Ta có. $y’=2ax+b;y’=0\Leftrightarrow x={{x}_{0}}=-\dfrac{b}{2a};{{U}_{C}}$
cực đại Theo định lý Vi- ét đối với phương trình bậc hai ẩn là ${{\omega }^{2}}$, ta có. ${{x}_{1}}+{{x}_{2}}=-\dfrac{b}{a}=2{{x}_{0}}\Leftrightarrow 2\omega _{0}^{2}=\omega _{1}^{2}+\omega _{2}^{2}\Leftrightarrow \omega _{0}^{2}=\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)$
Thay số vào ta được. ${{\omega }_{0}}=\sqrt{\dfrac{1}{2}\left( \omega _{1}^{2}+\omega _{2}^{2} \right)}=\sqrt{\dfrac{1}{2}\left( {{45}^{2}}+{{60}^{2}} \right)}=\dfrac{75}{\sqrt{2}}\left( rad/s \right)$
Và ${{\omega }_{0}}=2\pi . {{f}_{0}}=\dfrac{75}{\sqrt{2}}\left( \Omega \right)\Rightarrow {{f}_{0}}\approx 8,44\left( Hz \right)$
Câu 37.
Cho đoạn mạch không phân nhánh gồm R = 80 Ω cuộn dây có điện trở r = 20 Ω, độ tự cảm L = 0,318 H, tụ điện có điện dung C = 15,9 μF. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số f thay đổi được và điện áp hiệu dụng là 200 V. Để điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại thì tần số f phải điều chỉnh ở giá trị
[A]. 70,45 Hz.
[B]. 192,6 Hz.
[C]. 61,3 Hz.
[D]. 385,1 Hz.
Điều chỉnh f để công suất trên toàn mạch đạt giá trị cực đại $\Rightarrow $
Mạch xảy ra cộng hưởng Hay ${{Z}_{L}}={{Z}_{C}}\Leftrightarrow \omega =\dfrac{1}{\sqrt{LC}}=444,72\left( rad/s \right)\Rightarrow f=\dfrac{\omega }{2\pi }=70,78\left( Hz \right)$
Và ${{P}_{max}}=\dfrac{{{U}^{2}}}{R+r}=\dfrac{{{200}^{2}}}{100}=400\left( \text{W} \right)$
Câu 38.
Đoạn mạch xoay chiều RLC nối tiếp, cuộn dây thuần cảm với CR2 < 2L; điện áp hai đầu đoạn mạch là u = $u=U\sqrt{2}\cos \omega t$, có U không đổi và ω thay đổi được. Khi ω = ωC thì điện áp hai đầu tụ điện đạt cực đại và điện áp hiệu dụng hai đầu cuộn dây ${{U}_{L}}=\dfrac{{{U}_{R}}}{10}$. Hệ số công suất tiêu thụ của cả đoạn mạch là
[A]. 0,6
[B]. $\dfrac{1}{\sqrt{15}}$
[C]. $\dfrac{1}{\sqrt{26}}$
[D]. 0,8
Khi \[\omega ={{\omega }_{C}}\] điện áp hai đầu tụ điện đạt cực đại thì
\[\left\{ \begin{array}{l} Z_{C}^{2}={{Z}^{2}}+Z_{L}^{2} \\ {{U}_{L}}=\dfrac{{{U}_{R}}}{10}\Rightarrow {{Z}_{L}}=\dfrac{R}{10} \end{array} \right. \]
Mặt khác, lại có. $R=\sqrt{2{{Z}_{L}}. \left( {{Z}_{C}}-{{Z}_{L}} \right)}\Rightarrow 10{{Z}_{L}}=\sqrt{2{{Z}_{L}}. \left( {{Z}_{C}}-{{Z}_{L}} \right)}\Rightarrow 102Z_{L}^{2}=2{{Z}_{L}}{{Z}_{C}}\Rightarrow {{Z}_{C}}=51{{Z}_{L}}$
Tổng trở của đoạn mạch là. $Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{100Z_{L}^{2}+2500Z_{L}^{2}}=10\sqrt{26}{{Z}_{L}}$
Hệ số công suất tiêu thụ của cả đoạn mạch là $cos\varphi =\dfrac{R}{Z}=\dfrac{10{{Z}_{L}}}{10\sqrt{26}{{Z}_{L}}}=\dfrac{1}{\sqrt{26}}$
Câu 39.
Một mạch điện xoay chiều AB gồm điện trở thuần R , cuộn dây thuần cảm L, tụ điện C theo thứ tự mắc nối tiếp, với 2L > CR2. Gọi M là điểm nối giữa cuộn dây L và tụ điện C. Đặt vào 2 đầu đoạn mạch 1 điện áp xoay chiều có biểu thức $u=U\sqrt{2}\cos \omega t$ có U không đổi và ω thay đổi được. Thay đổi ω để điện áp hiệu dụng giữa hai bản tụ đạt giá trị cực đại UCmax = \[\dfrac{5}{4}U\]. Hệ số công suất của đoạn mạch AM là
[A]. $\dfrac{1}{\sqrt{3}}$.
[B]. \[\dfrac{2}{\sqrt{5}}\].
[C]. $\dfrac{1}{\sqrt{7}}$.
[D]. $\dfrac{2}{\sqrt{7}}$.
\[{{U}_{C}}=I. {{Z}_{C}}=\dfrac{U}{\omega C\sqrt{{{R}^{2}}+{{(\omega L-\dfrac{1}{\omega C})}^{2}}}}=\dfrac{U}{C\sqrt{{{\omega }^{2}}({{R}^{2}}+{{\omega }^{2}}{{L}^{2}}+\dfrac{1}{{{\omega }^{2}}{{C}^{2}}}-2\dfrac{L}{C}})}=\dfrac{U}{C\sqrt{Y}}\] \[{{U}_{C}}={{U}_{Cmax}}\]
khi \[Y\text{ }=\text{ }{{L}^{2}}{{\omega }^{4}}+\left( {{R}^{2}}-2\dfrac{L}{C} \right){{\omega }^{2}}+\dfrac{1}{{{C}^{2}}}\] có giá trị cực tiểu Ymin
Đặt \[x={{\omega }^{2}},Y={{L}^{2}}{{x}^{4}}+\left( {{R}^{2}}-2\dfrac{L}{C} \right){{x}^{2}}+\dfrac{1}{{{C}^{2}}}\]
Lấy đạo hàm của Y theo x, cho Y’ = 0
\[\Rightarrow x={{\omega }^{2}}=\dfrac{2\dfrac{L}{C}-{{R}^{2}}}{2{{L}^{2}}}=\dfrac{1}{LC}-\dfrac{{{R}^{2}}}{2{{L}^{2}}}\] Hay \[{{\omega }^{2}}=\dfrac{1}{LC}-\dfrac{{{R}^{2}}}{2{{L}^{2}}}\Rightarrow \omega =\dfrac{1}{L}\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}\]
Lai có. \[{{U}_{Cmax}}=\dfrac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}=\dfrac{5}{4}U\]
\[\Rightarrow {{R}^{2}}=\dfrac{20L}{25C}=0,8\dfrac{L}{C}\Rightarrow \dfrac{L}{C}=1,25{{R}^{2}}\](**)
Hệ số công suất của đoạn mạch AM.
\[cos{{\varphi }_{AM}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\omega }^{2}}{{L}^{2}}}}\]
\[{{Z}_{AM}}=\sqrt{{{R}^{2}}+{{\omega }^{2}}{{L}^{2}}}=\sqrt{{{R}^{2}}+\left( \dfrac{1}{LC}-\dfrac{{{R}^{2}}}{2{{L}^{2}}} \right){{L}^{2}}}=\sqrt{{{R}^{2}}+\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}=\dfrac{\sqrt{7}}{2}R\]
\[\Rightarrow cos{{\varphi }_{AM}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\omega }^{2}}{{L}^{2}}}}=\dfrac{2}{\sqrt{7}}\]
Câu 40.
Cho đoạn mạch R = 100 Ω, cuộn cảm thuần $L=\dfrac{1}{\pi }H$và tụ điện C. Điện áp giữa hai đầu đoạn mạch $u=220\sqrt{2}\cos 2\pi ft$ (V) với tần số f có thể thay đổi được. Khi f = fX thì điện áp hiệu dụng giữa hai bản tụ C đạt cực đại; giá trị lớn nhất này gấp $\dfrac{5}{3}$lần điện áp hiệu dụng giữa hai đầu đoạn mạch. Giá trị C và tần số fX lần lượt là
[A]. $\dfrac{{{4. 10}^{-5}}}{\pi }F;50\sqrt{2}\text{ Hz}\text{. }$
[B]. $\dfrac{{{10}^{-5}}}{\pi }F;\text{ }50\text{ Hz}\text{. }$
[C]. $\dfrac{{{10}^{-5}}}{2\pi }\text{F};\text{ }50\sqrt{2}\text{ Hz}\text{. }$
[D]. $\dfrac{{{4. 10}^{-5}}}{\pi }\text{F};\text{ }50\text{ Hz}\text{. }$
\[{{U}_{C}}=\dfrac{U{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\dfrac{1}{\omega C}\dfrac{U}{\sqrt{{{R}^{2}}+{{(\omega L-\dfrac{1}{\omega C})}^{2}}}}=\dfrac{1}{C}\dfrac{U}{\sqrt{{{L}^{2}}{{\omega }^{4}}+({{R}^{2}}-2\dfrac{L}{C}){{\omega }^{2}}+\dfrac{1}{{{C}^{2}}}}}\]
\[{{U}_{C}}=\text{ }{{U}_{Cmax}}\] khi \[{{\omega }^{2}}=\dfrac{2\dfrac{L}{C}-{{R}^{2}}}{2{{L}^{2}}}\]và \[{{U}_{Cmax}}\]= $\dfrac{1}{C}$$\dfrac{U}{\sqrt{\dfrac{4{{R}^{2}}\dfrac{L}{C}-{{R}^{4}}}{4{{L}^{2}}}}}$= $\dfrac{2LU}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}$ = $\dfrac{5U}{3}$
\[\Rightarrow \]6L = 5R $\sqrt{4LC-{{R}^{2}}{{C}^{2}}}$
\[\Rightarrow \]R2C2 – 4LC + $\dfrac{36{{L}^{2}}}{25{{R}^{2}}}$
\[\Rightarrow \] \[C=\dfrac{2L\pm 1,6L}{{{R}^{2}}}=\left( 2\pm 1,6 \right). \dfrac{{{10}^{-4}}}{\pi }\left( F \right)\]
\[\Rightarrow \] có 2 giá trị của \[{{C}_{1}}=\dfrac{3,{{6.. 10}^{-4}}}{\pi }\] và C2 = $\dfrac{{{4. 10}^{-5}}}{\pi }$F w2 = $\dfrac{2\dfrac{L}{C}-{{R}^{2}}}{2{{L}^{2}}}$ = $\dfrac{1}{LC}$ – $\dfrac{{{R}^{2}}}{2{{L}^{2}}}$ > 0 \[\Rightarrow \]C < $\dfrac{2L}{{{R}^{2}}}$ = $\dfrac{{{2. 10}^{-4}}}{\pi }$F
\[\Rightarrow \] loại nghiệm C1 \[{{C}_{X}}={{C}_{2}}=\dfrac{{{4. 10}^{-5}}}{\pi }\left( F \right)\]
\[\Rightarrow \] w2 = $\dfrac{1}{L{{C}_{2}}}$ – $\dfrac{{{R}^{2}}}{2{{L}^{2}}}$ = $\dfrac{{{10}^{5}}{{\pi }^{2}}}{4}$ – $\dfrac{{{100}^{2}}{{\pi }^{2}}}{2}$= 2. 104p2
\[\Rightarrow \]w= 100p$\sqrt{2}$ rad/s Do đó \[{{f}_{X}}=50\sqrt{2}Hz\]
Câu 41.
Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có độ tự cảm $L=\dfrac{25}{4\pi }$H, tụ điện có điện dung \[C=\dfrac{{{10}^{-3}}}{4,8\pi }\]F. Đặt vào hai đầu mạch điện áp xoay chiều $u=200\sqrt{2}\cos \left( \omega t+\varphi \right)$ có tần số góc $\omega $ hay đổi được. Thay đổi $\omega $, thấy hai giá trị \[~{{\omega }_{1}}=30\pi \sqrt{2}\]rad/s hoặc\[~{{\omega }_{2}}=40\pi \sqrt{2}\]rad/s thì điện áp hiệu dụng trên cuộn dây có giá trị bằng nhau. Điện áp hiệu dụng hai đầu cuộn dây đạt giá trị cực đại khi thay đổi ω là
[A]. $120\sqrt{5}$V.
[B]. $150\sqrt{2}$V.
[C]. $120\sqrt{3}$V.
[D]. $100\sqrt{2}$V.
Có 2 giá trị của $\omega $ làm điện áp hiệu dụng giữa hai đầu cuộn thuần cảm L có cùng 1 giá trị, tìm ${{\omega }_{L}}$ để ${{U}_{Lmax}}$ thì $\dfrac{1}{\omega _{L}^{2}}=\dfrac{1}{2}\left( \dfrac{1}{\omega _{1}^{2}}+\dfrac{1}{\omega _{2}^{2}} \right)\Rightarrow \omega _{L}^{2}=\dfrac{2\omega _{1}^{2}\omega _{2}^{2}}{\omega _{1}^{2}+\omega _{2}^{2}}$
Thay số vào, ta được. $\Rightarrow {{\omega }_{L}}=\sqrt{\dfrac{2\omega _{1}^{2}\omega _{2}^{2}}{\omega _{1}^{2}+\omega _{2}^{2}}}=\sqrt{\dfrac{2. {{\left( 30\pi \sqrt{2} \right)}^{2}}. {{\left( 40\pi \sqrt{2} \right)}^{2}}}{{{\left( 30\pi \sqrt{2} \right)}^{2}}+{{\left( 40\pi \sqrt{2} \right)}^{2}}}}=48\pi \left( rad/s \right)$
Ta có. ${{Z}_{L}}=L\omega =300\left( \Omega \right);{{Z}_{C}}=\dfrac{1}{C\omega }=100\left( \Omega \right)$
Lại có. $Z_{L}^{2}={{Z}^{2}}+Z_{C}^{2}\Rightarrow Z=\sqrt{Z_{L}^{2}-Z_{C}^{2}}=\sqrt{{{300}^{2}}-{{100}^{2}}}=200\sqrt{2}\left( \Omega \right)$
Điện áp hiệu dụng của đoạn mạch. $I=\dfrac{U}{Z}=\dfrac{200}{200\sqrt{2}}=\dfrac{1}{\sqrt{2}}\left( A \right)$
$\Rightarrow {{U}_{Cmax}}=I. {{Z}_{L}}=\dfrac{1}{\sqrt{2}}. 300=150\sqrt{2}\left( V \right)$
Câu 42.
Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm với CR2 < 2L. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức u = U cos2πft (V), trong đó U không đổi và tần số f thay đổi được. Điều chỉnh giá trị của f khi f = f1 thì khi đó UCmax và công suất của mạch là P = 0,75Pmax, khi f = f2 = f1+100Hz thì UL đạt ULmax. Giá trị f1; f2 lần lượt là
[A]. 150Hz, 250Hz.
[B]. 50Hz, 150Hz.
[C]. 250Hz, 350Hz.
[D]. 50Hz, 250Hz.
Ta có. \[P=UIcos\varphi =U. \dfrac{U}{Z}. \dfrac{R}{Z}=\dfrac{{{U}^{2}}}{R}. \dfrac{{{R}^{2}}}{{{Z}^{2}}}={{P}_{max}}. co{{s}^{2}}\varphi =0,75{{P}_{max}}\] \[\Rightarrow cos\varphi =\dfrac{\sqrt{3}}{2}=\sqrt{\dfrac{2{{f}_{C}}}{{{f}_{C}}+{{f}_{L}}}}=\sqrt{\dfrac{2{{f}_{1}}}{{{f}_{1}}+{{f}_{1}}+100}}\] \[\Rightarrow {{f}_{C}}={{f}_{1}}=150\left( Hz \right)\] Hay \[f={{f}_{2}}={{f}_{L}}={{f}_{1}}+100=250\left( Hz \right)\]
Câu 43.
Cho mạch điện xoay chiều AB theo thứ tự gồm điện trở thuần R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp. N là điểm nằm giữa cuộn dây và tụ điện. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức u = Uocosωt(V), trong đó Uo có giá trị không đổi, ω thay đổi được. Điều chỉnh ω để điện áp hiệu dụng trên tụ có giá trị cực đại, khi đó uAN lệch pha $\dfrac{2\pi }{5}$ (rad) so với uAB, công suất tiêu thụ của mạch khi đó là 100 W và hệ số công suất của đoạn mạch AN lớn hơn hệ số công suất của đoạn mạch AB. Khi điều chỉnh ω để công suất tiêu thụ của mạch đạt cực đại và giá trị cực đại đó bằng
[A]. $100\sqrt{2}$W.
[B]. 100 W.
[C]. 215 W.
[D]. $200\sqrt{3}$W.
Gọi \[{{\varphi }_{1}},{{\varphi }_{2}}\] lần lượt là góc hợp bởi \[\overrightarrow{{{u}_{AN}}};\overrightarrow{{{u}_{AB}}}\]
với \[\overrightarrow{{{u}_{R}}}\] ta có. \[\left\{ \begin{array}{l} tan{{\varphi }_{1}}. tan{{\varphi }_{2}}=\dfrac{1}{2} \\ tan\left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)=3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} tan{{\varphi }_{2}}=1,07 \\ tan{{\varphi }_{2}}=0,47 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} tan{{\varphi }_{1}}=0,47 \\ tan{{\varphi }_{1}}=1,07 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left[ \begin{array}{l} cos{{\varphi }_{1}}=0,68 \\ cos{{\varphi }_{1}}=0,91 \end{array} \right. \\ \left[ \begin{array}{l} cos{{\varphi }_{2}}=0,68 \\ cos{{\varphi }_{2}}=0,91 \end{array} \right. \end{array} \right. \Rightarrow \left\{ \begin{array}{l} cos{{\varphi }_{1}}=0,68 \\ cos{{\varphi }_{2}}=0,91 \end{array} \right. \left( cos{{\varphi }_{1}}<cos{{\varphi }_{2}} \right)\]
\[\Rightarrow {{P}_{max}}=\dfrac{P}{co{{s}^{2}}{{\varphi }_{1}}}=\dfrac{100}{{{\left( 0,68 \right)}^{2}}}\approx 216\left( W \right)\]gần 215 W
Câu 44.
Cho đoạn mạch AB gồm LRC mắc nối tiếp theo thứ tự. Cuộn cảm thuần, điện trở R = 50 Ω. Đặt vào hai đầu đoạn mạch điện áp xoay chiều$u=U\sqrt{2}\cos 2\pi ft$, có U không đổi, tần số f của dòng điện thay đổi được. Điều chỉnh f để điện áp hai đầu cuộn cảm đạt giá trị cực đại ${{U}_{L\max }}=U\sqrt{3}$. Khi đó điện áp hiệu dụng đoạn mạch chứa RC có giá trị 150 V. Công suất của mạch khi đó có giá trị gần đúng bằng
[A]. 148,6 W.
[B]. 150 W.
[C]. 192,5 W.
[D]. 139,2 W.
Khi \[\omega \] thay đổi để \[{{U}_{C}}\] lớn nhất thì \[{{\omega }_{C}}=\dfrac{\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}{L}. \] Hay \[{{Z}_{L}}=\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}\Leftrightarrow Z_{L}^{2}={{Z}_{L}}{{Z}_{C}}-\dfrac{{{R}^{2}}}{2}\Leftrightarrow \dfrac{{{R}^{2}}}{2}={{Z}_{L}}\left( {{Z}_{C}}-{{Z}_{L}} \right)\]
Mà. \[tan{{\alpha }_{1}}=\dfrac{{{Z}_{L}}}{R};tan{{\alpha }_{22}}=\dfrac{{{Z}_{C}}-{{Z}_{L}}}{R}\]
Nên ta có. \[tan{{\alpha }_{1}}. tan{{\alpha }_{2}}=\dfrac{1}{2}\]
Điều chỉnh f để điện áp hai đầu cuộn cảm đạt giá trị cực đại ${{U}_{L\max }}=U\sqrt{3}$.
Ta có. \[{{R}^{2}}=\sqrt{2{{Z}_{C}}\left( {{Z}_{L}}-{{Z}_{C}} \right)}\Rightarrow Z_{C}^{2}={{Z}_{L}}{{Z}_{C}}-\dfrac{{{R}^{2}}}{2}\]
\[\Leftrightarrow {{\left( {{Z}_{C}}-{{Z}_{L}} \right)}^{2}}-Z_{L}^{2}+Z_{C}^{2}+{{R}^{2}}=0\]
$\Leftrightarrow {{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}=3{{U}^{2}}-{{150}^{2}}\Leftrightarrow {{U}^{2}}=3{{U}^{2}}-{{150}^{2}}\Leftrightarrow 2{{U}^{2}}+U_{R}^{2}=150$ (1)
Mặt khác. ${{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}+U_{R}^{2}=U_{L}^{2}-U_{C}^{2}$ ${{U}_{C}}=U\sqrt{2}$ $U_{R}^{2}={{U}^{2}}\left( -4+2\sqrt{6} \right)$
Thay vào (1) $\Rightarrow {{U}_{R}}=83,53\left( V \right)\Rightarrow P=\dfrac{U_{R}^{2}}{R}=139,5\left( \text{W} \right)$
Câu 45.
Một đoạn mạch AB mắc nối tiếp theo thứ tự gồm R,C, cuộn dây không thuần cảm có độ tự cảm L, điện trở trong r = R (L = CR2). Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = U0cosωt (V), với ω thay đổi được. Khi ω = ω1 thì điện áp trên RC trễ pha hơn điện áp trên AB một góc α1 và có giá trị hiệu dụng U1. Khi ω = ω2 thì điện áp trên RC trễ pha hơn điện áp trên AB một góc α2 và có giá trị hiệu dụng U2. Biêt α1 + α2 =$\dfrac{\pi }{2}$ và U1 = kU2. Hệ số công suất khi ω = ω1 là.
[A]. \[\dfrac{1}{\sqrt{k+\dfrac{1}{k}}}\]
[B]. \[\dfrac{2}{\sqrt{k+\dfrac{1}{k}}}\]
[C]. \[\dfrac{1}{k+\dfrac{1}{k}}\]
[D]. \[\dfrac{2}{k+\dfrac{1}{k}}\]
Ta có. $tan{{\varphi }_{AM}}=-\dfrac{{{Z}_{C}}}{R};tan{{\varphi }_{MB}}=\dfrac{{{Z}_{L}}}{r}$ ${{u}_{AM}}$ vuông pha với ${{u}_{MB}}$ v
ới mọi tần số w. nên $tan{{\varphi }_{AM}}. tan{{\varphi }_{MB}}=-1\Leftrightarrow -\dfrac{{{Z}_{C}}}{R}. \dfrac{{{Z}_{L}}}{r}=-1\Leftrightarrow {{R}^{2}}={{Z}_{L}}{{Z}_{C}}\left( R=r \right)$
Vẽ giãn đồ vec tơ như hình vẽ.
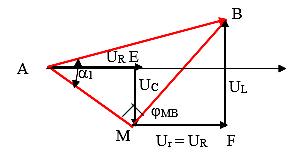
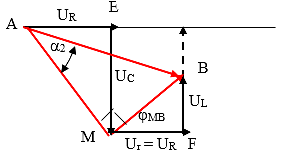
Ta luôn có UR = Ur \[\dfrac{{{U}_{C}}}{{{U}_{r}}}=\dfrac{{{U}_{R}}}{{{U}_{L}}}\Rightarrow \]
Hai tam giác vuông EAM và FBM đồng dạng $\dfrac{{{U}_{R}}}{{{U}_{L}}}$ = $\dfrac{{{U}_{C}}}{{{U}_{R}}}$ = $\dfrac{{{U}_{AM}}}{{{U}_{MB}}}$
\[{{U}_{AM}}={{U}_{AB}}cos\alpha =Ucos\alpha \] (*)
(α là góc trễ pha của uAM so với uAB) \[{{U}_{MB}}={{U}_{AB}}sin\alpha =Usin\alpha \](**)
Từ (*) và (**) \[\Rightarrow tan\alpha =\dfrac{{{U}_{MB}}}{{{U}_{AM}}}\]
Khi \[\omega ={{\omega }_{1}}~\] thì \[{{U}_{AM}}={{U}_{1}}=Ucos{{\alpha }_{1}}\]
Khi \[\omega ={{\omega }_{2}}~\] thì \[U{{}_{AM}}={{U}_{2}}=Ucos{{\alpha }_{2}}~=\text{ }Usin{{\alpha }_{1}}\]
(do α1 + α2 =$\dfrac{\pi }{2}$( Mà \[{{U}_{1}}=k{{U}_{2~~~}}\]
Suy ra. \[tan{{\alpha }_{1}}=\dfrac{{{U}_{2}}}{{{U}_{1}}}=\dfrac{1}{k}\]\[\Rightarrow {{U}_{MB}}={{U}_{AM}}tan{{\alpha }_{1}}=~\dfrac{1}{k}{{U}_{1}}\]
Từ đó suy ra. \[\dfrac{{{U}_{R}}}{{{U}_{L}}}=\dfrac{{{U}_{C}}}{{{U}_{R}}}=\dfrac{{{U}_{AM}}}{{{U}_{MB}}}=\dfrac{{{U}_{1}}}{\dfrac{1}{k}{{U}_{1}}}=k\]
\[\Rightarrow {{U}_{L}}=\dfrac{1}{k}{{U}_{R}}~~\left( 1 \right);~~{{U}_{C}}=k~{{U}_{R}}~(2)\]
\[U_{AB}^{2}={{U}^{2}}=U_{AM}^{2}+U_{MB}^{2}~=2U_{R}^{2}+U_{L}^{2}+U_{C}^{2}=\left( 2+\dfrac{1}{{{k}^{2}}}+{{k}^{2}} \right)U_{R}^{2}\Rightarrow U=\dfrac{\sqrt{{{k}^{4}}+2{{k}^{2}}+1}}{k}{{U}_{R}}\]
\[\Rightarrow cos{{\varphi }_{1}}=\dfrac{2{{U}_{R}}}{U}~=~\dfrac{2k}{{{k}^{2}}+1}=\dfrac{2}{k+\dfrac{1}{k}}\]
Câu 46.
Một đoạn mạch AB mắc nối tiếp theo thứ tự gồm R,C, cuộn dây không thuần cảm có độ tự cảm L, điện trở trong r = R (L = CR2). Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = U0cosωt(V), với ω thay đổi được. Khi ω = ω1 thì điện áp trên cuộn dây là${{u}_{d1}}={{U}_{1}}\sqrt{2}\cos \left( {{\omega }_{1}}t+{{\varphi }_{1}} \right)$. Khi ω = ω2 thì điện áp trên cuộn cảm ${{u}_{d2}}={{U}_{2}}\sqrt{2}\cos \left( {{\omega }_{2}}t+{{\varphi }_{2}} \right)$Biết φ1 + φ2 = $\dfrac{\pi }{2}$ và U1 = kU2. Hệ số công suất khi ω = ω1 là 0,28. Giá trị k là
[A]. 7
[B]. 0,7
[C]. 0,8
[D]. 8
Sử dụng kết quả bài 45, ta có \[cos{{\varphi }_{1}}=\dfrac{2{{U}_{R}}}{U}~=~\dfrac{2k}{{{k}^{2}}+1}=\dfrac{2}{k+\dfrac{1}{k}}\] Hay \[0,28=\dfrac{2}{k+\dfrac{1}{k}}\Leftrightarrow 0,28k+\dfrac{0,28}{k}=2\Leftrightarrow 0,28{{k}^{2}}-2k+0,28=0\Rightarrow \left[ \begin{array}{l} k=7 \\ k=\dfrac{1}{7} \end{array} \right. \]
Câu 47.
Đặt một điện áp \[u=U\sqrt{2}\cos \omega t\] vào hai đầu đọan mạch RLC mắc nối tiếp. Khi tần số f = f1, f = f1 + 150 Hz, f = f1 + 50 Hz thì hệ số công suất của mạch tương ứng là 1; 0,6 và$\dfrac{15}{17}$. Tần số để mạch cộng hưởng gần giá trị nào sau đây nhất?
[A]. 180Hz
[B]. 150 Hz
[C]. 120 Hz
[D]. 100 Hz
Ta có
\[cos\varphi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{{{R}^{2}}+{{(\omega L-\dfrac{1}{\omega C})}^{2}}}}\]
Khi \[{{f}_{1}}={{f}_{0}}\Rightarrow cos{{\varphi }_{1}}=1\Rightarrow \omega _{0}^{2}=\dfrac{1}{LC}\](1)
Khi \[f={{f}_{2}}\Rightarrow cos{{\varphi }_{2}}=0,6=\dfrac{R}{{{Z}_{2}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{\omega }_{2}}L-\dfrac{1}{C{{\omega }_{2}}} \right)}^{2}}}}\]
\[\Rightarrow 64{{R}^{2}}=36{{\left( {{\omega }_{2}}L\text{ }-\dfrac{1}{{{\omega }_{2}}C} \right)}^{2}}\](2)
Khi \[f={{f}_{3}}\Rightarrow cos{{\varphi }_{3}}=\dfrac{15}{17}=\dfrac{R}{{{Z}_{3}}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{\omega }_{3}}L-\dfrac{1}{C{{\omega }_{3}}} \right)}^{2}}}}\Rightarrow 64{{R}^{2}}=15{{\left( {{\omega }_{3}}L-\dfrac{1}{C{{\omega }_{3}}} \right)}^{2}}\](3)
Từ (2) và (3) \[\Rightarrow 2\left( {{\omega }_{2}}L\text{ }-\dfrac{1}{{{\omega }_{2}}C} \right)=5\left( {{\omega }_{3}}L\text{ }-\dfrac{1}{C{{\omega }_{3}}} \right)\Leftrightarrow L\left( 2{{\omega }_{2}}-5{{\omega }_{3}} \right)=\dfrac{1}{C}\left( \dfrac{2}{{{\omega }_{2}}}-\dfrac{5}{{{\omega }_{3}}} \right)=\dfrac{1}{C}\dfrac{2{{\omega }_{3}}-5{{\omega }_{2}}}{{{\omega }_{2}}. {{\omega }_{3}}}\]
\[\Rightarrow \left( 2{{\omega }_{2}}-\text{ }5{{\omega }_{3}} \right)=\dfrac{1}{LC}\dfrac{2{{\omega }_{3}}-5{{\omega }_{2}}}{{{\omega }_{2}}. {{\omega }_{3}}}={{\omega }_{0}}^{2}. \dfrac{2{{\omega }_{3}}-5{{\omega }_{2}}}{{{\omega }_{2}}. {{\omega }_{3}}}\]
Do \[\omega =2\pi f\] nên \[2{{f}_{2}}-5{{f}_{3}}=f_{0}^{2}. \dfrac{2{{f}_{3}}-5{{f}_{2}}}{{{f}_{2}}. {{f}_{3}}}\] (4)
Thay vào (4):
\[{{f}_{2}}={{f}_{0}}+150\left( Hz \right);{{f}_{3}}={{f}_{0}}+50\left( Hz \right)\]
Ta được phương trình
\[{{f}_{0}}^{2}-125{{f}_{0}}+3750=0\Rightarrow \left[ \begin{array}{l}
{{f}_{0}}=75\left( Hz \right) \\
{{f}_{0}}=50\left( Hz \right)
\end{array} \right. \] gần 100 Hz nhât
Câu 48.
Đặt vào hai đầu AB điện áp xoay chiều \[u=U\sqrt{2}\cos \omega t\]vào hai đầu đoạn mạch RLC mắc nối tiếp với CR2 < 2L. Khi f = f1 thì UL = U. Khi f = f2 = 2f1 thì UC = U. Khi f = fL thì ULmax và dòng điện trễ pha hơn u góc φ. Giá trị φ là
[A]. 0,785 rad
[B]. 0,686 rad
[C]. 0,686 rad
[D]. 0,886 rad
f = f1 thì UL = U = \[{{f}_{1}}=\dfrac{{{f}_{L}}}{\sqrt{2}}\]
f = f2 thì UC = U = \[{{f}_{2}}=\sqrt{2}{{f}_{C}}\]
Khi ULmax ta có: \[\cos \varphi =\sqrt{\dfrac{2{{f}_{C}}}{{{f}_{L}}+{{f}_{C}}}}=\sqrt{\dfrac{\sqrt{2}{{f}_{2}}}{\sqrt{2}{{f}_{1}}+\dfrac{{{f}_{2}}}{\sqrt{2}}}}=\sqrt{\dfrac{\sqrt{2}{{f}_{2}}}{\sqrt{2}\dfrac{3}{2}{{f}_{2}}+\dfrac{{{f}_{2}}}{\sqrt{2}}}}=\dfrac{\sqrt{2}}{2}\]= \[\varphi =\dfrac{\pi }{4}=0,785rad\]
Câu 49.
Đặt vào hai đầu AB điện áp xoay chiều \[u=U\sqrt{2}\cos \omega t\]vào hai đầu đoạn mạch AB theo thứ tự điện trở thuẩn, cuộn dây thuần cảm,tụ C mắc nối tiếp. N là điểm giữa cuộn dây và tụ điện. Điều chỉnh ω để điện áp hiệu dụng trên tụ có giá trị cực đại, khi đó uAN lệch pha 1,2373 rad so với uAB, công suất tiêu thụ khi đó là 300 W. Khi điều chỉnh ω để công suất tiêu thụ của mạch đạt giá trị cực đại thì giá trị đó bằng.
[A]. 300 W.
[B]. 4500 W.
[C]. 250 W.
[D]. 525 W.
Gọi \[{{\varphi }_{1}},{{\varphi }_{2}}\] lần lượt là góc hợp bởi \[\overrightarrow{{{u}_{AN}}};\overrightarrow{{{u}_{AB}}}\] với \[\overrightarrow{{{u}_{R}}}\]
ta có. \[\left\{ \begin{array}{l} tan{{\varphi }_{1}}. tan{{\varphi }_{2}}=\dfrac{1}{2} \\ tan\left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)=2,89 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} tan{{\varphi }_{2}}=0,89 \\ tan{{\varphi }_{2}}=0,56 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} tan{{\varphi }_{1}}=0,56 \\ tan{{\varphi }_{1}}=0,89 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left[ \begin{array}{l} cos{{\varphi }_{1}}=0,87 \\ cos{{\varphi }_{1}}=0,75 \end{array} \right. \\ \left[ \begin{array}{l} cos{{\varphi }_{2}}=0,75 \\ cos{{\varphi }_{2}}=0,87 \end{array} \right. \end{array} \right. \Rightarrow \left\{ \begin{array}{l} cos{{\varphi }_{1}}=0,75 \\ cos{{\varphi }_{2}}=0,87 \end{array} \right. \left( cos{{\varphi }_{1}}<cos{{\varphi }_{2}} \right)\]
\[\Rightarrow {{P}_{max}}=\dfrac{P}{co{{s}^{2}}{{\varphi }_{1}}}=\dfrac{100}{{{\left( 0,75 \right)}^{2}}}\approx 533\left( W \right)\]gần 525 W (Do sai số)
Câu 50.
Đoạn mạch xoay chiều AB có RLC nối tiếp, cuộn dây thuần cảm với CR2 < 2L; điện áp hai đầu đoạn mạch là uAB = U\[\sqrt{2}\]cos ωt , U ổn định và ω thay đổi. Khi ω = ωC thì điện áp hai đầu tụ C cực đại, khi đó điện áp tức hai đầu đoạn mạch AN (gồm RL) và AB lệch pha nhau là \[\varphi \]. Giá trị nhỏ nhất của tan\[\varphi \] là
[A]. $2\sqrt{2}$
[B]. $\dfrac{\sqrt{2}}{2}$
[C]. 2,5
[D]. $\sqrt{3}$
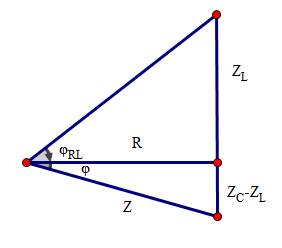
Khi \[\omega \] thay đổi để \[{{U}_{C}}\] lớn nhất thì \[{{\omega }_{C}}=\dfrac{\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}{L}. \] Hay \[{{Z}_{L}}=\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}\Leftrightarrow Z_{L}^{2}={{Z}_{L}}{{Z}_{C}}-\dfrac{{{R}^{2}}}{2}\Leftrightarrow \dfrac{{{R}^{2}}}{2}={{Z}_{L}}\left( {{Z}_{C}}-{{Z}_{L}} \right)\]
Mà. \[tan{{\alpha }_{1}}=\dfrac{{{Z}_{L}}}{R};tan{{\alpha }_{22}}=\dfrac{{{Z}_{C}}-{{Z}_{L}}}{R}\]
Nên ta có. \[tan{{\alpha }_{1}}. tan{{\alpha }_{2}}=\dfrac{1}{2}\]
Khi w = wC thì điện áp hai đầu tụ C cực đại thì \[{{R}^{2}}=2{{Z}_{L}}\left( {{Z}_{C}}-{{Z}_{L}} \right)\Rightarrow \dfrac{1}{2}=\dfrac{{{Z}_{L}}}{R}. \dfrac{{{Z}_{C}}-{{Z}_{L}}}{R}\]
Đặt \[{{\varphi }_{AB}}=b,{{\varphi }_{RL}}=a\]
\[tana. tanb=\dfrac{1}{2}\] và \[tan\varphi =tan\left( a+b \right)=\dfrac{tana+tanb}{1-tana. tanb}=2\left( tana+tanb \right)\]
Để có giá trị nhỏ nhất của \[\alpha \] thì. \[tana+tanb\ge 2\sqrt{tana. tanb}=\sqrt{2}\]
\[\Rightarrow tan\varphi \ge 2\sqrt{2}\Leftrightarrow \varphi \ge 70,{{5}^{o}}\]
Câu 51.
Cho mạch điện xoay chiều mắc nối tiếp gồm các phần tử điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Mạch chỉ có tần số góc thay đổi được. Khi ω = ω1 = 100\[\pi \] rad/s thì điện áp hiệu dụng hai đầu cuộn cảm cực đại. Khi ω = ω2 = 2ω1 thì điện áp hai đầu tụ điện cực đại. Biết rằng khi giá trị ω = ω1 thì ZL + 3ZC = 400 Ω. Giá trị L bằng
[A]. $\dfrac{4}{7\pi }$H.
[B]. $\dfrac{4}{3\pi }$H.
[C]. $\dfrac{3}{4\pi }$H.
[D]. $\dfrac{7}{4\pi }$H.
\[{{U}_{L}}={{U}_{Lmax}}\] khi khi \[\omega ={{\omega }_{1}}=\dfrac{1}{C\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}}\](1) và \[{{U}_{C}}={{U}_{Cmax}}\] khi khi \[\omega ={{\omega }_{2}}=\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}\](2)
Lấy \[\left( 1 \right)x\left( 2 \right)\Rightarrow 2\omega _{1}^{2}=\dfrac{1}{LC}\Rightarrow 2{{Z}_{L}}={{Z}_{C}}\]
Ta có. \[~~{{Z}_{L}}+3{{Z}_{C}}=400\left( \Omega \right)\Rightarrow 7{{Z}_{L}}=400\left( \Omega \right)\Rightarrow {{Z}_{L}}=\dfrac{400}{7}\left( \Omega \right)\Rightarrow L=\dfrac{4}{7\pi }\left( H \right)\]
Câu 52.
Mạch điệnAB gồm R, L, C nối tiếp, uAB = U cosωt. Chỉ có ω thay đổi được. Giá trị hiệu dụng của điện áp ở hai đầu các phần tử R, L, C lần lượt là UR; UL; UC. Cho ω tăng dần từ 0 đến thì thứ tự đạt cực đại của các điện áp trên là
[A]. UC; UR; UL.
[B]. UC; UL; UR.
[C]. UL; UR; UC.
[D]. UR; UL; UC.
Điều kiện để \[{{U}_{L}},\text{ }{{U}_{C}}\] có cực trị là biểu thức trong căn của $X=\sqrt{\dfrac{L}{C}-\dfrac{{{R}^{2}}}{2}}$ phải dương, nghĩa là phải có. $2L>C. {{R}^{2}}$. Và khi đó ta có thể chứng minh được. \[{{\omega }_{C}}<{{\omega }_{R}}<{{\omega }_{L}}\]. Nghĩa là, khi tăng dần tốc độ góc ω từ 0 đến ∞ thì điện áp trên các linh kiện sẽ lần lượt đạt cực đại theo thứ tự. C, R, L.
Câu 53.
ĐH-2013). Đặt điện áp \[u=120\sqrt{2}c\text{os}2\pi ft\text{ }\left( V \right)\](\[f\]thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với CR2 < 2L. Khi f = f1 thì điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại. Khi f = f2 = f1\[\sqrt{2}\]thì điện áp hiệu dụng giữa hai đầu điện trở đạt cực đại. Khi f = f3 thì điện áp giữa hai đầu cuộn cảm đạt cực đại ULmax. Giá trị của ULmax gần giá trị nào nhất sau đây.
[A]. 85 V.
[B]. 145 V.
[C]. 57 V.
[D]. 173 V.
(ĐH-2013). Khi f biến đổi đến f1 để UCmax thì ω biến đổi.
\[\omega _{0C}^{2}=\dfrac{1}{LC}-\dfrac{{{R}^{2}}}{2{{L}^{2}}}\]
Khi f biến đổi đến f3 để ULmax thì ω biến đổi.
\[\omega _{0L}^{2}=LC-\dfrac{{{R}^{2}}{{C}^{2}}}{2}\]
Khi f biến đổi đến f2 = \[\sqrt{2}\]f1 để URmax thì ω biến đổi.
\[\omega _{2}^{2}=\dfrac{1}{LC}={{\omega }_{0C}}. {{\omega }_{0L}}\]
\[\Leftrightarrow f_{2}^{2}={{f}_{1}}. {{f}_{3}}\Rightarrow {{f}_{3}}=2{{f}_{1}}=\sqrt{2}{{f}_{2}}\Rightarrow {{Z}_{{{L}_{3}}}}=2{{Z}_{{{C}_{3}}}}\]
Với\[C{{R}^{2}}<2L\Rightarrow {{R}^{2}}<2. {{Z}_{L3}}. {{Z}_{C3}}\].
Ta có. \[{{U}_{L\max }}=\dfrac{U. {{Z}_{L3}}}{\sqrt{{{R}^{2}}+{{\left( Z_{L3}^{{}}-{{Z}_{C3}} \right)}^{2}}}}\ge \dfrac{U. {{Z}_{L3}}}{\sqrt{Z_{L3}^{2}+Z_{_{C3}}^{2}}}=\dfrac{2U}{\sqrt{5}}\]
\[\Rightarrow {{U}_{Lmax}}~>107,33\text{ }V\] Giá trị của ULmax gần giá trị 145V nhất