Chuyên đề điện xoay chiều mạch RLC nối tiếp, vật lí lớp 12
Phần 2: Mạch RLC nối tiếp phương pháp giản đồ véc tơ
Câu 1.
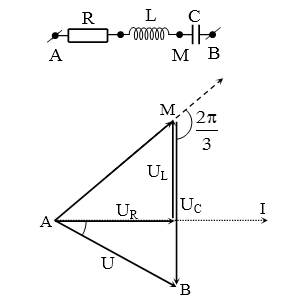
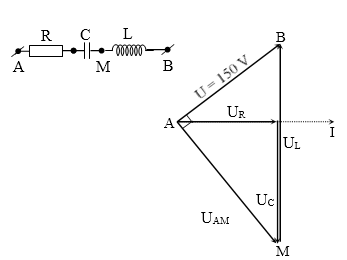
Đặt điện áp $u=220\sqrt{2}\cos 100\pi t$ (V) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần L, đoạn MB chỉ có tụ điện C. Biết điện áp giữa hai đầu đoạn mạch AM và điện áp giữa hai đầu đoạn mạch MB có giá trị hiệu dụng bằng nhau nhưng lệch pha nhau $\dfrac{2\pi }{3}$. Điện áp hiệu dụng giữa hai đầu đoạn mạch AM bằng
[A]. $220\sqrt{2}$V.
[B]. $\dfrac{220}{\sqrt{3}}$V.
[C]. 220 V.
[D]. 110 V.
Nhìn vào giản đồ vectơ dễ thấy ∆AMB đều.
→ UAM = UMB = U = 220 V.
Câu 2.
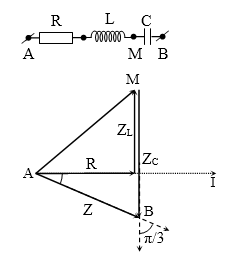
Đặt điện áp xoay chiều tần số 50 Hz vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R = $100\sqrt{3}$ Ω mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn MB chỉ có tụ điện có điện dung $C=\dfrac{0,05}{\pi }$mF. Biết điện áp giữa hai đầu đoạn mạch MB và điện áp giữa hai đầu đoạn mạch AB lệch pha nhau$\dfrac{\pi }{3}$. Giá trị L bằng
[A]. $\dfrac{2}{\pi }H$
[B]. $\dfrac{1}{\pi }H$.
[C]. $\dfrac{\sqrt{3}}{\pi }H$.
[D]. $\dfrac{3}{\pi }H$
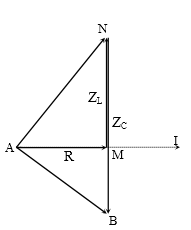
Nhìn giản đồ dễ thấy u chậm pha hơn i góc $\dfrac{\pi }{6}$.
→$\tan \varphi =tan\left( -\dfrac{\pi }{6} \right)=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}=-\dfrac{1}{\sqrt{3}}\to {{Z}_{L}}=100\text{ }\Omega .$
→ $L=\dfrac{1}{\pi }H$.
Câu 3.
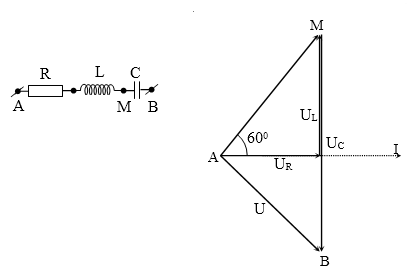
Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần L, đoạn MB chỉ có tụ điện C. Biết điện áp hiệu dụng giữa hai đầu đoạn đoạn mạch MB và AM thỏa mãn: ${{U}_{MB}}={{U}_{AM}}\sqrt{3}$, điện áp giữa hai đầu AM lệch pha $\dfrac{\pi }{3}$ so với cường độ dòng điện trong mạch. Độ lệch pha của điện áp giữa hai đầu AM so với điện áp giữa hai đầu đoạn mạch trên là
[A]. 0
[B]. $\dfrac{\pi }{2}$.
[C]. $-\dfrac{\pi }{3}$.
[D]. $\dfrac{2\pi }{3}$.
Bài cho ${{U}_{MB}}={{U}_{AM}}\sqrt{3}$.
Theo giản đồ: góc AMB = 300
→$U_{AB}^{2}=U_{AM}^{2}+U_{MB}^{2}-2{{U}_{AM}}.{{U}_{MB}}.\cos {{30}^{0}}$
→${{U}_{AB}}={{U}_{AM}}$ → ∆AMB cân tại A → góc MAB = 1200.
Câu 4. ĐH2012
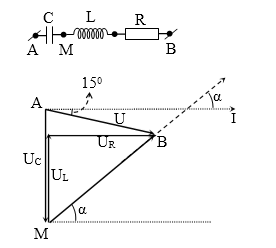
Đặt điện áp u = U0cosωt (U0 và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha $\dfrac{\pi }{12}$ so với điện áp giữa hai đầu đoạn mạch. Điện áp đoạn mạch MB lệch pha so với dòng điện góc
[A]. \[\dfrac{\pi }{12}\]
[B]. \[\dfrac{\pi }{6}\]
[C]. \[\dfrac{\pi }{3}\]
[D]. \[\dfrac{\pi }{4}\]
Bài cho ${{U}_{AM}}={{U}_{MB}}$, do đó ∆AMB cân tại M.
→ Mà u vài i lệch pha $\dfrac{\pi }{12}={{15}^{0}}$ hay góc I0AB =150.
→ Dễ dàng tính được độ lệch pha uMB với i là α = 600.
Câu 5.
Đặt điện áp $u=150\sqrt{2}\cos 100\pi t$ (V) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R = 60 Ω mắc nối tiếp với tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{0,8\pi }F$, đoạn MB chỉ có cuộn cảm L. Biết điện áp giữa hai đầu đoạn mạch AM và điện áp giữa hai đầu đoạn mạch AB vuông pha nhau. Điện áp hiệu dụng giữa hai đầu đoạn mạch MB bằng
[A]. 200 V.
[B]. 35 V.
[C]. 250 V.
[D]. 237 V.
ZC = 80 Ω → UR:UC = 3:4
Nhìn vào giản đồ vectơ:
\[\tan \widehat{\text{A}MB}=\dfrac{{{U}_{R}}}{{{U}_{C}}}=\dfrac{3}{4}\to \sin \widehat{\text{A}MB}=\dfrac{3}{5}=\dfrac{150}{{{U}_{MB}}}\]
→ UMB = 250 V.
Câu 6.
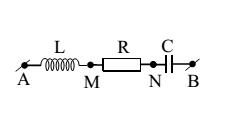
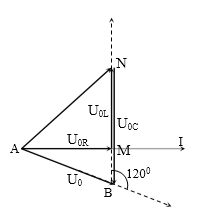
Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB (chứa cuộn cảm thuần) như hình vẽ thì thấy điện áp hai đầu đoạn mạch AN và MB lần lượt là ${{u}_{AN}}=100\cos \left( 100\pi t \right)V$ và ${{u}_{MB}}=100\sqrt{3}\cos \left( 100\pi t-\dfrac{\pi }{2} \right)V$. Điện áp hiệu dụng đặt vào hai đầu đoạn mạch AB là
[A]. 250 V
[B]. $25\sqrt{14}$ V
[C]. $25\sqrt{7}$ V
[D]. $50\sqrt{7}$ V
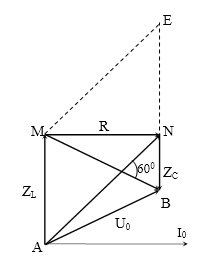
Bài cho uAN vuông pha với uMB!
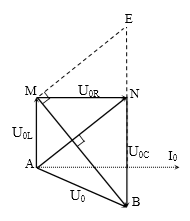
Kẻ giản đồ vectơ: AN = $100\text{ }V$ và MB = $100\sqrt{3}$ V
Kẻ thêm đường thẳng qua M // AN cắt BN tại E.
Dễ thấy: ME = AN = 100 V.
Xét ∆MEB vuông tại M có MN là đường cao.
→$\dfrac{1}{M{{N}^{2}}}=\dfrac{1}{M{{E}^{2}}}+\dfrac{1}{M{{B}^{2}}}\to {{U}_{0\text{R}}}=MN=50\sqrt{3}\text{ V}$
→${{U}_{0L}}=AM=\sqrt{A{{N}^{2}}-M{{N}^{2}}}=50\text{ V}$
→${{U}_{0C}}=NB=\sqrt{B{{M}^{2}}-M{{N}^{2}}}=150\text{ V}$
Vậy: ${{U}_{0}}=\sqrt{U_{0\text{R}}^{2}+{{\left( {{U}_{0L}}-{{U}_{0C}} \right)}^{2}}}=50\sqrt{7}\text{ V}\to \text{U = 25}\sqrt{14}\text{ V}$.
Câu 7.
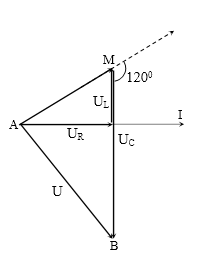
Đặt điện áp $u=120\sqrt{2}\cos 100\pi t$ (V) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần L, đoạn MB chỉ có tụ điện C. Biết điện áp giữa hai đầu đoạn mạch AM bằng một nửa điện áp giữa hai đầu đoạn mạch MB và lệch pha nhau một góc 1200 . Điện áp hiệu dụng giữa hai đầu đoạn mạch AM gần với giá trị nào sau đây nhất ?
[A]. 34,34 V.
[B]. 65,28 V.
[C]. 127,02 V.
[D]. 112,37 V.
Bài cho: MB = 2AM, AB = 120 V.
Áp dụng định lý hàm cos cho ∆AMB
\[\text{A}{{B}^{2}}=A{{M}^{2}}+M{{B}^{2}}-2.AM.MB.\cos {{60}^{0}}=3.\text{A}{{M}^{2}}\to AM=\dfrac{AB}{\sqrt{3}}=40\sqrt{3}\text{ }V.\]
Câu 8.
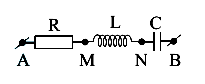
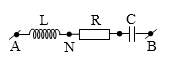
Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB như hình vẽ thì thấy điện áp hai đầu đoạn mạch MB là ${{u}_{MB}}=80\sin \left( 100\pi t-\dfrac{\pi }{3} \right)V$. Biết R = 40 Ω, $C=\dfrac{{{10}^{-4}}}{\pi }F$, cuộn cảm thuần $L=\dfrac{3}{5\pi }H$. Biểu thức điện áp đặt vào hai đầu đoạn mạch AB là
[A]. $u=160\cos \left( 100\pi t-\dfrac{\pi }{3} \right)V$
[B]. $u = 160\sqrt 2 \cos \left( {100\pi t – \dfrac{{11\pi }}{{12}}} \right)V$
[C]. $u=80\sqrt{2}\cos \left( 100\pi t-\dfrac{7\pi }{12} \right)V$
[D]. $u=80\cos \left( 100\pi t-\dfrac{3\pi }{4} \right)V$
\[{{u}_{MB}}=80\sin \left( 100\pi t-\dfrac{\pi }{3} \right)V=80\cos \left( 100\pi t-\dfrac{5\pi }{6} \right)V\]
R = 40 Ω, ZL = 60 Ω, ZC = 100 Ω → \[\text{Z}=40\sqrt{2}\text{ }\Omega \]
Lại có: U0: U0MB = Z:ZMB → U0 = $80\sqrt{2}$ V.
u nhanh pha hơn uMB góc $\dfrac{\pi }{4}$, do đó: ${{\varphi }_{u}}-{{\varphi }_{{{u}_{MB}}}}=\dfrac{\pi }{4}\to {{\varphi }_{u}}=-\dfrac{7\pi }{12}$
→$u=80\sqrt{2}\cos \left( 100\pi t-\dfrac{7\pi }{12} \right)V$.
Câu 9.
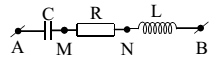
Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB (chứa cuộn cảm thuần) như hình vẽ thì thấy điện áp hai đầu đoạn mạch AN và MB lần lượt là là${{u}_{AN}}=200\cos \left( 100\pi t-\dfrac{\pi }{6} \right)V$ và ${{u}_{MB}}=200\cos \left( 100\pi t+\dfrac{\pi }{3} \right)V$. Biểu thức điện áp đặt vào hai đầu đoạn mạch AB là
[A]. $u=40\sqrt{5}\cos \left( 100\pi t+\dfrac{\pi }{12} \right)V$
[B]. $u=40\sqrt{5}\cos \left( 100\pi t \right)V$
[C]. $u=100\sqrt{2}\cos \left( 100\pi t \right)V$
[D]. $u=100\sqrt{2}\cos \left( 100\pi t+\dfrac{\pi }{12} \right)V$
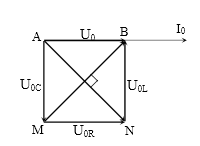
Kẻ giản đồ vectơ với AN = MB = 200 V, AN $\bot $ MB
→ AMNB là hình vuông → U0 = AB = $100\sqrt{2}$ V
u nhanh pha hơn uAN góc $\dfrac{\pi }{4}$→ ${{\varphi }_{u}}={{\varphi }_{{{u}_{AN}}}}+\dfrac{\pi }{4}=\dfrac{\pi }{12}$
Vậy: $u=100\sqrt{2}\cos \left( 100\pi t+\dfrac{\pi }{12} \right)V$.
Câu 10.
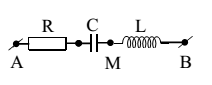
Đặt điện áp xoay chiều $u=200\sqrt{2}\cos \left( 100\pi t+\dfrac{\pi }{6} \right)V$vào hai đầu đoạn mạch AB (chứa cuộn cảm thuần) như hình vẽ thì thấy cường độ dòng điện i trong mạch chậm pha hơn so với u góc $\dfrac{\pi }{3}$, nhanh pha hơn uAM góc $\dfrac{\pi }{3}$và có giá trị hiệu dụng là 1 A. Giá trị L và C là?
[A]. L = 1,103 H và C = 18,378 μF.
[B]. L = 0,637 H và C = 31,8 μF.
[C]. L = 0,882 H và C = 22,919 μF.
[D]. L = 0,318 H và C = 63,6 μF.
\[\text{Z}=\dfrac{U}{I}=200\text{ }\Omega \].
Nhìn giản đồ thấy ∆AMB cân tại A.
→ Z = ZAM = 200 Ω
→ \[{{\text{Z}}_{C}}=100\sqrt{3}\text{ }\Omega \to {{Z}_{L}}=2{{\text{Z}}_{C}}=200\sqrt{3}\text{ }\Omega \]
→ L = 1,103 H và C = 18,378 μF
Câu 11.
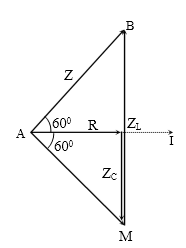
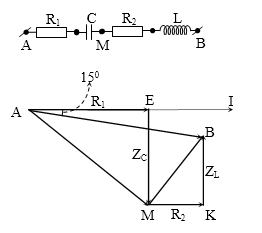
Một đoạn mạch AB gồm hai đoạn mạch nhỏ AM và MB mắc nối tiếp với nhau. Đoạn mạch AM gồm điện trở R1 mắc nối tiếp với cuộn thuần cảm có độ tự cảm L. Đoạn mạch MB gồm điện trở R2 mắc nối tiếp với tụ điện có điện dung C. Khi đặt vào hai đầu AB một điện áp xoay chiều có giá trị hiệu dụng U thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM và MB lần lượt là U1 và U2. Biết ${{U}^{2}}=U_{1}^{2}+U_{2}^{2}$. Hệ thức liên nào sau đây là đúng?
[A]. L = CR1R2.
[B]. C = LR1R2.
[C]. LC = R1R2
[D]. LR1 = CR2
${{U}^{2}}=U_{1}^{2}+U_{2}^{2}$→ ∆AMB vuông tại M.
Do đó: ∆AEM ~ ∆BKM
→ $\dfrac{{{R}_{1}}}{{{Z}_{C}}}=\dfrac{{{Z}_{L}}}{{{R}_{2}}}\to {{R}_{1}}{{R}_{2}}={{Z}_{L}}{{Z}_{C}}=\dfrac{L}{C}$ .
Câu 12.
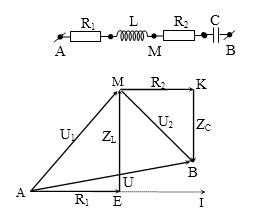
Đoạn mạch AB gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp theo đúng thứ tự trên. Gọi M là điểm nối giữa cuộn cảm thuần và tụ điện. Vôn kế có điện trở vô cùng lớn mắc giữa A và M. Điện áp ở hai đầu mạch AB là $u=100\sqrt{2}\cos \omega t$(V) . Biết 2LCω2 = 1. Số chỉ của vôn kế bằng
[A]. 80 V.
[B]. 200 V.
[C]. 100 V.
[D]. 120 V.
2LCω2 = 1 → 2ZL = ZC
→ ∆AMB cân tại A → UAM = U = 100 V.
Câu 13.
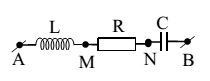
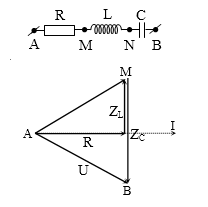
Đặt vào hai đầu mạch AB điện áp xoay chiều như hình vẽ thì thấy rằng: ${{u}_{AN}}=150c\text{os}(100\pi t+\dfrac{\pi }{3})\,(V)$;${{u}_{MB}}=50\sqrt{6}c\text{os}(100\pi t-\dfrac{\pi }{12})\,(V)$. Biết R = 25 Ω. Cường độ dòng điện hiệu dụng qua mạch là
[A]. $\sqrt{2}$ A.
[B]. 3,3 A.
[C]. 3 A.
[D]. 6 A.
Kẻ giản đồ vectơ:
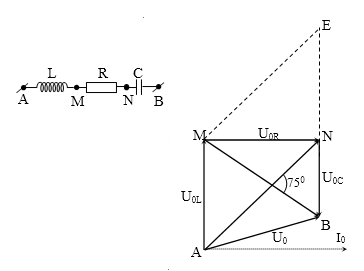
AN và MB hợp nhau góc 750.
AN = 150 V và MB = $50\sqrt{6}$ V
Kẻ thêm đường thẳng qua M // AN cắt BN tại E → ME = AN = 150 V
Xét ∆MBE với góc EMB = 750 có diện tích:
${{S}_{\Delta MBE}}=\dfrac{1}{2}MN.BE=\dfrac{1}{2}MB.ME\sin {{75}^{0}}$ $\to MN=\dfrac{MB.ME\sin {{75}^{0}}}{BE}=\dfrac{MB.ME\sin {{75}^{0}}}{\sqrt{M{{B}^{2}}+M{{E}^{2}}-2MB.ME.\cos {{75}^{0}}}}=75\sqrt{2}$V
→${{U}_{0R}}=MN=75\sqrt{2}\text{ V}\to {{\text{U}}_{R}}=75\text{V}\to \text{I = }\dfrac{{{U}_{R}}}{R}=3\text{ }A$.
Câu 14.
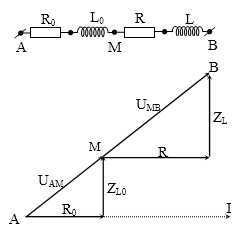
Đoạn mạch AM gồm cuộn cảm thuần có độ tự cảm L mắc nối tiếp với một điện trở R0 = 60Ω ; đoạn mạch MB gồm một điện trở thuần có giá trị R mắc nối tiếp một hộp kín chứa một trong hai phần tử : cuộn dây thuần cảm hoặc tụ điện . Khi đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có giá trị hiệu dụng 200V thì điện áp hiệu dụng trên đoạn AM và MB lần lượt là 80V và 120V. Giá trị của R và phần tử trong hộp kín là:
[A]. R = 90 Ω ; tụ điện.
[B]. R = 60 Ω ; cuộn cảm
[C]. R = 90 Ω ; cuộn cảm.
[D]. R = 60 Ω ; tụ điện.
${{U}_{AB}}={{U}_{AM}}+{{U}_{MB}}$→ AMB thẳng hàng
→ Hộp kín chứa cuộn cảm thuần L.
→ $\dfrac{{{R}_{0}}}{R}=\dfrac{AM}{MB}\to R=90\text{ }\Omega $.
Câu 15.
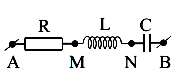
Đoạn mạch AB gồm một cuộn cảm thuần có độ tự cảm $L=\dfrac{1,2}{\pi }$ H, một tụ điện có điện dung $C=\dfrac{{{10}^{-4}}}{\pi }$F và một điện trở thuần R = 50 Ω mắc như hình vẽ. Điện áp giữa hai đầu đoạn mạch AB có tần số 50 Hz. Độ lệch pha của điện áp giữa hai điểm A, N đối với điện áp giữa hai điểm M, B là
[A]. 220.
[B]. 910.
[C]. 40.
[D]. 780
$\tan \left( {{\varphi }_{{{u}_{AN}}}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}}{R}=2,4$→ uAN nhanh pha hơn i góc 67,380
Đoạn mạch MB chỉ có L và C mà ZL>ZC → uMB nhanh pha hơn i góc 900
=> uAN lệch pha uMB góc xấp xỉ 220.
Câu 16.
Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM có điện trở R1 = 20 Ω mắc nối tiếp với tụ điện C, đoạn mạch MB có điện trở R2 mắc với cuộn dây thuần cảm có độ tự cảm L. Đặt vào hai đầu đoạn mạch AB điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi thì cường độ dòng điện trong mạch sớm pha $\dfrac{\pi }{12}$so với điện áp của hai đầu đoạn mạch. điện áp hai đầu AM và MB có giá trị hiệu dụng thỏa mãn ${{U}_{AM}}=\sqrt{3}{{U}_{MB}}$và lệch pha nhau $\dfrac{\pi }{2}$rad. Giá trị của R2 là
[A]. $30\,\Omega $
[B]. $20\,\Omega $
[C]. $20\sqrt{3}\,\Omega $
[D]. $\dfrac{20}{\sqrt{3}}\,\Omega $
Ta có AM $\bot $ MB
→ $\tan \widehat{BAM}=\dfrac{MB}{AM}=\dfrac{1}{\sqrt{3}}\to \widehat{BAM}={{30}^{0}}$
→ $\widehat{IAB}={{45}^{0}}$→ ∆AEM vuông cân tại E
→ $AM={{R}_{1}}\sqrt{2}=20\sqrt{2}\text{ }\Omega \to MB=20\sqrt{\dfrac{2}{3}}\to {{R}_{2}}=\dfrac{MB}{\sqrt{2}}=\dfrac{20}{\sqrt{3}}\text{ }\Omega .$
Câu 17.
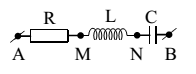
Cho một mạch điện RLC nối tiếp như hình vẽ. Biết L = 0,8/π (H), C = 10-4/π (F). Đặt vào hai đầu đoạn mạch một điện áp có biểu thức u = Uocos100πt V thì thấy điện áp uAN lệch pha π/2 so với u. Giá trị R là
[A]. R = 20 Ω.
[B]. R = 40 Ω.
[C]. R = 48 Ω.
[D]. R = 140 Ω.
∆ABN vuông tại có A có: AM2 = NM.MB
→ R2 = ZL.(ZC – ZL) → R = 40 Ω
Câu 18.
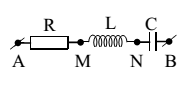
Cho một mạch điện RLC nối tiếp như hình vẽ. Biết\[R=100\sqrt{3}\,\Omega \], cuộn cảm thuần. Đặt vào hai đầu đoạn mạch điện áp có biểu thức\[{{u}_{AB}}=200\sqrt{2}c\text{os}(100\pi t)\,V\]thì điện áp hai đầu đoạn mạch MN nhanh pha hơn hiệu thế hai đầu đoạn mạch AB một góc $\dfrac{2\pi }{3}$. Cường độ dòng điện i qua mạch có biểu thức nào sau đây?
[A]. $i=\sqrt{2}c\text{os}\left( 100\pi t+\dfrac{\pi }{6} \right)A.$
[B]. $i=\sqrt{2}c\text{os}\left( 100\pi t+\dfrac{\pi }{3} \right)A.$
[C]. $i=\sqrt{2}c\text{os}\left( 100\pi t-\dfrac{\pi }{3} \right)A.$
[D]. $i=\sqrt{2}c\text{os}\left( 100\pi t-\dfrac{\pi }{6} \right)A.$
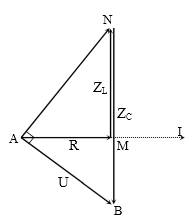
Qua giản đồ thấy i nhanh pha hơn u góc 300
Do đó ${{\varphi }_{i}}={{\varphi }_{u}}+\dfrac{\pi }{6}=0+\dfrac{\pi }{6}=\dfrac{\pi }{6}$
\[\cos \widehat{IAB}=\dfrac{{{U}_{0R}}}{{{U}_{0}}}\to {{U}_{0R}}=100\sqrt{6}\]V → ${{I}_{0}}=\dfrac{{{U}_{0R}}}{R}=\sqrt{2}$A.
Vậy: $i=\sqrt{2}c\text{os}\left( 100\pi t+\dfrac{\pi }{6} \right)A.$
Câu 19.
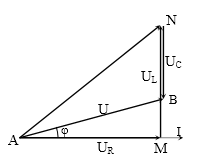
Cho mạch điện như hình vẽ có điện áp hiệu dụng UAB = 300 V, UNB = 140 V, dòng điện i trễ pha so với uAB một góc φ (với cosφ = 0,8), cuộn cảm thuần. Điện áp hiệu dụng giữa hai điểm A và N là ?
[A]. 100 V.
[B]. 200 V.
[C]. 300 V.
[D]. 400 V.
AB = 300 V, NB = 140 V, cosφ = 0,8. Tính AN = ?
$\cos \varphi =\dfrac{AM}{AB}=0,8\to AM=240\text{ V}$
→$MB=\sqrt{A{{B}^{2}}-A{{M}^{2}}}=180\text{ V}$
→ MN = MB + NB = 320 V
Vậy: $AN=\sqrt{A{{M}^{2}}+M{{N}^{2}}}=400\text{ V}$.
Câu 20.
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \left( 100\pi t-\dfrac{\pi }{3} \right)$ vào hai đầu đoạn mạch AB như hình vẽ thì thấy điện áp hai đầu đoạn mạch AN và MB lệch pha nhau $\dfrac{\pi }{3}$. Biết LC = 2.10-5 (L tính theo Henry, C tính theo Fara). Lấy π2 = 10. Pha ban đầu dòng điện chạy trong mạch là?
[A]. -1,42 rad
[B]. -0,68 rad
[C]. 0,68 rad
[D]. -0,38 rad
Đầu tiên ta có: \[\dfrac{{{Z}_{L}}}{{{Z}_{C}}}=LC{{\omega }^{2}}=2\]. Đặt ZC = 1 → ZL = 2.
Kẻ giản đồ vectơ: AN và MB hợp nhau góc 600.
Kẻ thêm đường thẳng qua M // AN cắt BN tại E.
Ta có: NE = AM = 2.
Xét ∆MBE với góc EMB = 600 có diện tích:
${{S}_{\Delta MBE}}=\dfrac{1}{2}MN.BE=\dfrac{1}{2}MB.ME\sin {{60}^{0}}\to 3R=\sqrt{\left( {{R}^{2}}+1 \right)\left( {{R}^{2}}+4 \right)}.\dfrac{\sqrt{3}}{2}$
$ \to 12{R^2} = \left( {{R^2} + 1} \right)\left( {{R^2} + 4} \right) \to \left[ \begin{array}{l}R = \sqrt {\dfrac{{7 + \sqrt {33} }}{2}} \left( {\widehat {BME} = {{60}^0}} \right)\\R = \sqrt {\dfrac{{7 – \sqrt {33} }}{2}} (\widehat {BME} = {120^0}) \to loi\end{array} \right.$
Vậy: $\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}\to {{\varphi }_{u}}-{{\varphi }_{i}}\approx 0,377\text{ rad}\to {{\varphi }_{i}}\approx -1,424\text{ rad}$.
Cách khác (phương pháp đại số):
${{\varphi }_{RL}}-{{\varphi }_{RC}}=\dfrac{\pi }{3}\Rightarrow \tan \left( {{\varphi }_{RL}}-{{\varphi }_{RC}} \right)=\sqrt{3}\Leftrightarrow \dfrac{\tan {{\varphi }_{RL}}-\tan {{\varphi }_{RC}}}{1+\tan {{\varphi }_{RL}}.\tan {{\varphi }_{RC}}}=\sqrt{3}$
$\Rightarrow \dfrac{\dfrac{2}{R}+\dfrac{1}{R}}{1-\dfrac{2}{{{R}^{2}}}}=\sqrt{3}$$\Leftrightarrow \dfrac{2}{{{R}^{2}}}+\dfrac{\sqrt{3}}{R}-1=0$→ $R=\sqrt{\dfrac{7+\sqrt{33}}{2}}$
Câu 21.
Đặt điện áp xoay chiều hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R1 = 100 Ω mắc nối tiếp với cuộn cảm thuần có độ tự cảm${{L}_{1}}=\dfrac{1}{\pi }$ H. Đoạn MB gồm điện trở thuần R2 mắc nối tiếp với cuộn cảm thuần có độ tự cảm ${{L}_{2}}=\dfrac{0,2}{\pi }H$. Biết ${{U}_{AB}}={{U}_{AM}}+{{U}_{MB}}$. Giá trị R2 bằng
[A]. 20 Ω.
[B]. 50 Ω.
[C]. 100 Ω.
[D]. 200 Ω.
Tương tự câu 14: \[\dfrac{{{R}_{2}}}{{{R}_{1}}}=\dfrac{{{Z}_{L2}}}{{{Z}_{L1}}}\to {{R}_{2}}=20\text{ }\Omega \].
Câu 22. ĐH2009
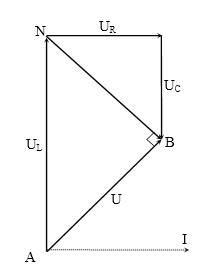
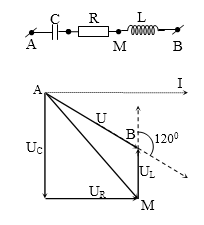
Đặt một điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch AB gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C mắc nối tiếp theo thứ tự trên. Gọi UL, UR và UC lần lượt là các điện áp hiệu dụng giữa hai đầu mỗi phần tử. Biết điện áp giữa hai đầu đoạn mạch AB lệch pha $\dfrac{\pi }{2}$ so với hai đầu điện áp giữa giữa hai đầu đoạn mạch NB (đoạn mạch NB gồm R và C). Hệ thức nào dưới đây đúng
[A]. \[U_{L}^{2}=U_{R}^{2}+U_{C}^{2}+{{U}^{2}}\]
[B]. \[{{U}^{2}}=U_{R}^{2}+U_{L}^{2}+U_{C}^{2}\]
[C]. \[U_{R}^{2}=U_{L}^{2}+U_{C}^{2}+U\]
[D]. \[U_{C}^{2}=U_{R}^{2}+U_{L}^{2}+U\]
Rõ ràng: \[U_{L}^{2}=U_{R}^{2}+U_{C}^{2}+{{U}^{2}}\]
Câu 23. ĐH2010
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM có điện trở thuần 50 Ω mắc nối tiếp với cuộn cảm thuần có độ tự cảm $\dfrac{1}{\pi }$ H, đoạn mạch MB chỉ có tụ điện. Đặt điện áp u = U0cos100πt (V) vào hai đầu đoạn mạch AB thì thấy điện áp hai đầu đoạn mạch AB lệch pha $\dfrac{\pi }{2}$ so với điện áp hai đầu đoạn mạch AM. Giá trị của điện dung của tụ điện bằng
[A]. $\dfrac{{{4.10}^{-5}}}{\pi }F$
[B]. $\dfrac{{{8.10}^{-5}}}{\pi }F$
[C]. $\dfrac{{{2.10}^{-5}}}{\pi }F$
[D]. $\dfrac{{{10}^{-5}}}{\pi }F$
∆ABN vuông tại có A có: AM2 = NM.MB
→ R2 = ZL.(ZC – ZL) → ZC = 125 Ω →$C=\dfrac{{{8.10}^{-5}}}{\pi }F$
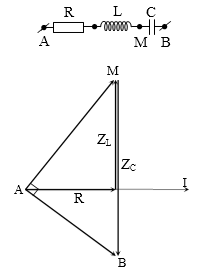
Câu 24.
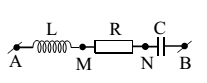
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \left( 100\pi t \right)V$vào hai đầu đoạn mạch AB như hình vẽ thì thấy điện áp hai đầu đoạn mạch AN và MB lệch pha nhau $\dfrac{\pi }{2}$. Biết $L=\dfrac{4}{\pi }H$, $C=\dfrac{{{10}^{-4}}}{\pi }F$. Giá trị điện trở R là
[A]. 100 Ω
[B]. $100\sqrt{2}\text{ }\Omega $
[C]. 200 Ω
[D]. 300 Ω
Tương tự ví dụ trong video bài giảng: \[{{\text{R}}^{2}}={{Z}_{L}}.{{Z}_{C}}\to \] R = 200 Ω.
Câu 25.
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \left( 100\pi t \right)V$vào hai đầu đoạn mạch AB như hình vẽ thì thấy điện áp hai đầu đoạn mạch AN và MB lệch pha nhau $\dfrac{\pi }{4}$. Biết $L=\dfrac{1}{\pi }H$, $C=\dfrac{{{10}^{-4}}}{2\pi }F$. Giá trị điện trở R xấp xỉ là là
[A]. 356 Ω.
[B]. 242 Ω.
[C]. 173 Ω.
[D]. 186 Ω.
Tương tự, có thể làm theo hai cách như câu 20.
Câu 26.
Đặt điện áp xoay chiều $u = {{U}_{0}}\cos \left( 100\pi t \right)V$ vào hai đầu đoạn mạch RLC thì thấy u nhanh pha$\dfrac{3\pi }{4}$ so với uC. Biết $L=\dfrac{1,8}{\pi }H$, $C=\dfrac{{{10}^{-4}}}{\pi }F$. Giá trị điện trở R là
[A]. 80 Ω
[B]. $80\sqrt{3}\text{ }\Omega $
[C]. $100\sqrt{2}\text{ }\Omega $
[D]. $100\sqrt{3}\text{ }\Omega $
Bài cho ${{\varphi }_{u}}={{\varphi }_{{{u}_{C}}}}+\dfrac{3\pi }{4}$
mà ta luôn có ${{\varphi }_{i}}={{\varphi }_{{{u}_{C}}}}+\dfrac{\pi }{2}$
$\to {{\varphi }_{u}}-{{\varphi }_{i}}=\dfrac{\pi }{4}\to \tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}=1\to Z=80\text{ }\Omega .$
Câu 27.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch xoay chiều AB gồm hai đoạn mạch AM (chứa tụ C nối tiếp với điện trở R) nối tiếp với đoạn mạch MB (chứa cuộn cảm thuần) thì điện áp hiệu dụng hai đầu AM gấp $\sqrt{7}$ lần điện áp hiệu dụng giữa hai đầu MB và điện áp giữa hai đầu MB lệch pha $\dfrac{2\pi }{3}$ so với hai đầu đoạn mạch. Tỉ số điện áp hiệu dụng giữa hai đầu đoạn mạch và hai đầu cuộn cảm là
[A]. 0,5.
[B]. 2.
[C]. $\dfrac{1}{3}$.
[D]. 3.
Bài cho \[\text{A}M=MB\sqrt{7}\]
Áp dụng định lý hàm cos cho ∆AMB:
\[\text{A}{{M}^{2}}=A{{B}^{2}}+M{{B}^{2}}-2AB.MB.\cos {{120}^{0}}\]
→\[7M{{B}^{2}}=A{{B}^{2}}+M{{B}^{2}}+AB.MB.\]
→ \[A{{B}^{2}}+AB.MB-6M{{B}^{2}}=0\to AB=2MB\].
Câu 28.
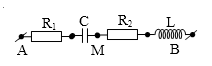
Đặt điện áp $\text{u = U}\sqrt{\text{2}}\text{cos100}\pi \text{t (V)}$ vào hai đầu đoạn mạch AB gồm hai đoạn AM và MB mắc nối tiếp. Trong đoạn AM có điện trở thuần ${{\text{R}}_{\text{1}}}\text{= 50}\Omega $ mắc nối tiếp với tụ điện có điện dung $\text{C = }\dfrac{\text{1}{{\text{0}}^{\text{-3}}}}{\text{5}\pi }\text{F}$. Trong đoạn MB có điện trở thuần ${{\text{R}}_{\text{2}}}$mắc nối tiếp với cuộn cảm thuần có tự cảm L . Điện áp giữa hai điểm A,M lệch pha một góc $\dfrac{\text{7}\pi }{\text{12}}$ so với điện áp giữa hai điểm M,B. Độ lệch pha của điện áp giữa hai điểm M,B so với cường độ dòng điện trong mạch là
[A]. $\dfrac{\pi }{\text{6}}$.
[B]. $\dfrac{\pi }{\text{3}}$.
[C]. $\text{- }\dfrac{\pi }{\text{3}}$.
[D]. $\text{- }\dfrac{\pi }{\text{6}}$.
$\tan \left( {{\varphi }_{{{u}_{AM}}}}-{{\varphi }_{i}} \right)=-\dfrac{{{Z}_{C}}}{{{R}_{1}}}=-1$ → i nhanh pha hơn uAM góc 450
Bài lại cho uMB nhanh pha hơn so với uAM góc $\dfrac{7\pi }{12}$ tức 1050.
→ uMB nhanh pha hơn i góc 105 – 45 = 600.