Chuyên đề tổng hợp dao động điều hòa, vật lí lớp 12
Câu 1.
Dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tấn số, biên độ $A_{1}$ và $A_{2}$ có biên độ A thỏa mãn điều kiện nào ?
[A]. A ≤ $A_{1}$ + $A_{2}$
[B]. |$A_{1}$ – $A_{2}$ | ≤ A ≤ $A_{1}$ + $A_{2}$
[C]. A = |$A_{1}$ – $A_{2}$ |
[D]. A ≥ |$A_{1}$ – $A_{2}$ |
Khi ${{\overrightarrow{A}}_{1}}\uparrow \uparrow {{\overrightarrow{A}}_{2}}$ Amax = A1 + A2
Khi ${{\overrightarrow{A}}_{1}}\uparrow \downarrow {{\overrightarrow{A}}_{2}}$ Amin = |A1 – A2|
→ |A1 – A2| ≤ A ≤ A1 + A2
Câu 2.
Dao động của một vật là tổng hợp của hai dao động điều hoà cùng phương, cùng tấn số, biên độ $A_{1}$ và $A_{2}$. Biên độ của dao động tổng hợp đạt giá trị cực đại là
[A]. $A_{1}$ + $A_{2}$ khi hai dao động thành phần cùng pha
[B]. \[2\sqrt{A_{1}^{2}+A_{2}^{2}}\] khi hai dao động thành phần cùng pha
[C]. |$A_{1}$ – $A_{2}$ | khi hai dao động thành phần ngược pha
[D]. \[\sqrt{A_{1}^{2}+A_{2}^{2}}\]khi hai dao động vuông pha
Khi ${{\overrightarrow{A}}_{1}}\uparrow \uparrow {{\overrightarrow{A}}_{2}}$ (hai dao động cùng pha) → Amax = A1 + A2
Câu 3.
Dao động của một vật là tổng hợp của hai dao động điều hoà cùng phương, cùng tấn số, biên độ $A_{1}$ và $A_{2}$ Biên độ của dao động tổng hợp đạt giá trị cực tiểu là
[A]. $A_{1}$ + $A_{2}$ khi hai dao động thành phần cùng pha
[B]. \[2\sqrt{A_{1}^{2}+A_{2}^{2}}\] khi hai dao động thành phần cùng pha
[C]. |$A_{1}$ – $A_{2}$ | khi hai dao động thành phần ngược pha
[D]. \[\sqrt{A_{1}^{2}+A_{2}^{2}}\]khi hai dao động vuông pha
Khi ${{\overrightarrow{A}}_{1}}\uparrow \downarrow {{\overrightarrow{A}}_{2}}$ (Hai dao động ngược pha) → Amin = |A1 – A2|
Câu 4.
Biên độ của dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số không phụ thuộc vào
[A]. biên độ của dao động thành phần thứ nhất.
[B]. biên độ của dao động thành phần thứ hai
[C]. độ lệch pha của hai dao động thành phần
[D]. tần số chung của hai dao động thành phần
Biên độ của dao động tổng hợp được xác định: ${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2A_{1}^{{}}A_{2}^{{}}\text{cos}\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)$
→ A không phụ thuộc tần số chung của hai dao động thành phần.
Câu 5.
Khi tổng hợp hai dao động cùng phương, cùng tần số và khác nhau pha ban đầu thì thấy pha của dao động tổng hợp cùng pha với dao động thứ hai. Kết luận nào sau đây đúng?
[A]. Hai dao động có cùng biên độ
[B]. Hai dao động vuông pha
[C]. Biên độ của dao động thứ hai lớn hơn biên độ của dao động thứ nhất và hai dao động ngược pha
[D]. Hai dao động kệch pha nhau 1200
Ta có: x = x1 + x2. Do x và x2 cùng pha nên có hai trường hợp
TH1: x1 và x2 cùng pha → Loại do đề bài cho khác pha
TH2: x1 và x2 ngược pha và biên độ A1 < A2
Câu 6.
Cho 2 dao động cùng phương, cùng tần số có phương trình $x_{1}$ = 7cos(πt + \[{\varphi _1}\]); $x_{2}$ = 2cos(πt + \[{\varphi _2}\]) cm. Khi thay đổi pha ban đầu của hai dao động thành phần thì biên độ của dao động tổng hợp có giá trị cực đại và cực tiểu lần lượt là
[A]. 9 cm; 4 cm
[B]. 9 cm; 5 cm
[C]. 9 cm; 7 cm
[D]. 7 cm; 5 cm
Amax = A1 + A2 = 7 + 2 = 9 cm
Amin = |A1 – A2| = 7 – 2 = 5 cm
Câu 7.
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số, có phương trình dao động lần lượt là $x_{1}$ = 7cos(5t + \[{\varphi _1}\])cm; $x_{2}$ = 3cos(5t + \[{\varphi _2}\]) cm. Khi thay đổi pha ban đầu của hai dao động thành phần thì gia tốc cực đại của vật lớn nhất mà có thể đạt là
[A]. 250 $cm/s^2$
[B]. 25 $m/s^2$
[C]. 2,5 $cm/s^2$
[D]. 0,25 $m/s^2$
Amax = A1 + A2 = 7 + 3 = 10 cm
amax = ω2Amax = 52.10 = 250 cm/s2
Câu 8.
Hai dao động điều hòa thành phần cùng phương, cùng tần số, có biên độ lần lượt là 8 cm và 12 cm, biên độ dao động tổng hợp có thể nhận giá trị
[A]. A = 5 cm
[B]. A = 2 cm
[C]. A = 21 cm.
[D]. A = 3 cm.
Amax = A1 + A2 = 12 + 8 = 20 cm
Amin = |A1 – A2| = 12 – 8 = 4 cm
→ 4 ≤ A ≤ 20 → A = 5cm thỏa mãn
Câu 9.
Hai dao động điều hòa thành phần cùng phương, cùng tần số, có biên độ lần lượt là 6 cm và 8 cm, biên độ dao động tổng hợp không thể nhận giá trị
[A]. A = 4 cm.
[B]. A = 8 cm
[C]. A = 6 cm
[D]. A = 15 cm.
Amax = A1 + A2 = 8 + 6 = 14 cm
Amin = |A1 – A2| = 8 – 6 = 2 cm
→ 2 ≤ A ≤ 14 → A = 15cm không thỏa mãn
Câu 10.
Hai dao động điều hòa thành phần cùng phương, cùng tần số, cùng pha có biên độ là $A_{1}$ và $A_{2}$ với $A_{2}$ = 3$A_{1}$ thì dao động tổng hợp có biên độ là
[A]. $A_{1}$
[B]. 2$A_{1}$
[C]. 3$A_{1}$
[D]. 4$A_{1}$
Hai dao động cùng pha: Amax = A1 + A2 = A1 + 3A1 = 4A1
Câu 11.
Hai dao động thành phần có biên độ 4 cm và 12 cm. Biên độ dao động tổng hợp có thể nhận giá trị:
[A]. 48cm.
[B]. 3 cm
[C]. 4cm
[D]. 9 cm
Amax = A1 + A2 = 12 + 4 = 16 cm
Amin = |A1 – A2| = 12 – 4 = 8 cm
→ 8 ≤ A ≤ 16 → A = 9 cm thỏa mãn
Câu 12.
Cho hai dao động cùng phương: \[{{x}_{1}}=3\cos (\omega t+{{\varphi }_{1}})\text{ }cm\] và \[{{x}_{2}}=4\cos (\omega t+{{\varphi }_{2}})\text{ }cm\]. Biết dao động tổng hợp của hai dao động trên có biên độ bằng 5 cm. Chọn hệ thức liên hệ đúng giữa φ1 và φ2
[A]. \[{{\varphi }_{2}}-{{\varphi }_{1}}=\left( 2k+1 \right)\dfrac{\pi }{4}\]
[B]. \[{{\varphi }_{2}}-{{\varphi }_{1}}=2k\pi \]
[C]. \[{{\varphi }_{2}}-{{\varphi }_{1}}=\left( 2k+1 \right)\dfrac{\pi }{2}\]
[D]. \[{{\varphi }_{2}}-{{\varphi }_{1}}=\left( 2k+1 \right)\pi \]
Nhận thấy 52 = 32 + 42 → x1 và x2 vuông pha nhau
Ta có: \[{{\varphi }_{2}}-{{\varphi }_{1}}=\left( 2k+1 \right)\dfrac{\pi }{2}\]
Câu 13.
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình $x_{1}$ = 3sin(10t + \[\dfrac{\pi }{3}\]) cm và $x_{2}$ = 4cos(10t – \[\dfrac{\pi }{6}\]) cm. Biên độ dao động tổng hợp của vật là
[A]. 1 cm
[B]. 5 cm
[C]. 5 mm
[D]. 7 cm
x1 = 3sin(10t + \[\dfrac{\pi }{3}\]) = 3cos(10t + \[\dfrac{\pi }{3}-\dfrac{\pi }{2}\]) = 3cos(10t + \[-\dfrac{\pi }{6}\])
Do x1 và x2 cùng pha nên A = A1 + A2 = 7 cm
→ A = 5 cm
Câu 14.
Hai dao động điều hòa cùng phương, cùng tần số, có biên độ lần lượt là 4,5cm và 6,0 cm; lệch pha nhau \[\pi \]. Dao động tổng hợp của hai dao động này có biên độ bằng
[A]. 1,5cm
[B]. 7,5cm
[C]. 5,0cm
[D]. 10,5cm.
Do x1 và x2 ngược pha (lệch pha nhau π) nên A = |A1 – A2| = 6 – 4,5 = 1,5 cm
Câu 15.
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình là $x_{1}$ = 3cos(20t + \[\dfrac{\pi }{3}\]) cm và $x_{2}$ = 4cos(20t – \[\dfrac{\pi }{6}\]) cm. Biên độ dao động tổng hợp của vật là
[A]. 1 cm
[B]. 5 cm
[C]. 5 mm
[D]. 7 cm
Biên độ của dao động tổng hợp được xác định:
${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2A_{1}^{{}}A_{2}^{{}}\text{cos}\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)={{3}^{2}}+{{4}^{2}}+2.3.4.c\text{os}\left( \dfrac{\pi }{3}-\dfrac{-\pi }{6} \right)=25$
→ A = 5 cm
Câu 16.
Khi tổng hợp hai dao động điều hoà cùng phương cùng tần số có biên độ thành phần 4 cm và 4$\sqrt{3}$cm được biên độ tổng hợp là 8 cm. Hai dao động thành phần đó
[A]. cùng pha với nhau.
[B]. lệch pha $\dfrac{\pi }{3}$.
[C]. vuông pha với nhau.
[D]. lệch pha $\dfrac{\pi }{6}$.
Biên độ của dao động tổng hợp được xác định:
${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2A_{1}^{{}}A_{2}^{{}}\text{cos}\Delta \varphi \Rightarrow \text{cos}\Delta \varphi =\dfrac{{{A}^{2}}-\left( A_{1}^{2}+A_{2}^{2} \right)}{2A_{1}^{{}}A_{2}^{{}}}=\dfrac{{{8}^{2}}-\left[ {{4}^{2}}+{{\left( 4\sqrt{3} \right)}^{2}} \right]}{2.4.4\sqrt{3}}=0\Rightarrow \Delta \varphi =\dfrac{\pi }{2}$
Câu 17.
Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình lần lượt là $x_{1}$=Acos\[\omega \]t và $x_{2}$ = Asin\[\omega \]t. Biên độ dao động của vật là
[A]. $\sqrt{3}$A
[B]. A
[C]. $\sqrt{2}$A.
[D]. 2A
${{x}_{2}}=Asin\omega t=Acos\left( \omega t-\dfrac{\pi }{2} \right)$
\[{{x}_{1}}=Acos\omega t\]
Hai dao động vuông pha nhau → ${{A}_{th}}=\sqrt{{{A}^{2}}+{{A}^{2}}}=A\sqrt{2}$
Câu 18.
Hai dao động điều hòa thành phần cùng phương, cùng tần số, dao động vuông pha có biên độ là $A_{1}$ và $A_{2}$ thỏa mãn 3$A_{2}$ = 4$A_{1}$ thì dao động tổng hợp có biên độ là
[A]. A = (5/4)$A_{1}$
[B]. A = (5/3)$A_{1}$
[C]. A = 3$A_{1}$
[D]. A = 3$A_{1}$
\[3{{A}_{2}}=\text{ }4{{A}_{1}}\Rightarrow {{A}_{2}}=\dfrac{4}{3}{{A}_{1}}\]
Hai dao động vuông pha nhau
→ Ath = $\sqrt{A_{1}^{2}+A_{2}^{2}}=\sqrt{A_{1}^{2}+{{\left( \dfrac{4}{3}{{A}_{1}} \right)}^{2}}}=\dfrac{5}{3}{{A}_{1}}$
Câu 19.
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số 50 Hz, có biên độ lần lượt là 8 cm và 6 cm và cùng pha nhau thì dao động tổng hợp có biên độ và tần số lần lượt là
[A]. A = 10 cm và f = 100 Hz
[B]. A = 10 cm và f = 50 Hz.
[C]. A = 14 cm và f = 100 Hz.
[D]. A = 14 cm và f = 50 Hz
+ Tần số của dao động tổng hợp bằng tần số dao động thành phần: f = 50 Hz
+ Hai dao động cùng pha: A = A1 + A2 = 8 + 6 = 14 cm
Câu 20.
Biên độ dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tấn số, cùng biên độ A và lệch pha nhau \[\dfrac{2\pi }{3}\] là
[A]. \[A\sqrt{2}\]
[B]. \[\dfrac{A\sqrt{3}}{3}\]
[C]. \[\dfrac{A\sqrt{3}}{2}\]
[D]. A.
Cách 1. Biên độ của dao động tổng hợp được xác định:
$A_{th}^{2}=A_{1}^{2}+A_{2}^{2}+2A_{1}^{{}}A_{2}^{{}}\text{cos}\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)={{A}^{2}}+{{A}^{2}}+2.A.A.c\text{os}\left( \dfrac{2\pi }{3} \right)={{A}^{2}}$ → Ath = A
Cách 2. Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: \[1\angle \dfrac{2\text{ }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }1\text{ }\!\!~\!\!\text{ }\angle 0\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}1\text{ }\!\!~\!\!\text{ }\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}\to {{A}_{th}}=\text{ }A\]
Câu 21.
Biên độ dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tấn số, cùng biên độ A và lệch pha nhau \[\dfrac{\pi }{3}\] là:
[A]. \[A\sqrt{2}\]
[B]. \[A\sqrt{3}\]
[C]. \[\dfrac{A\sqrt{3}}{2}\]
[D]. \[\dfrac{A\sqrt{3}}{3}\]
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $1\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }1\text{ }\!\!~\!\!\text{ }\angle 0\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}\sqrt{3}\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\Rightarrow {{A}_{th}}=A\sqrt{3}$
Câu 22.
Hai dao động điều hoà cùng phương có phương trình dao động lần lượt là ${{x}_{1}}=4\text{cos}\left( 10\pi t-\dfrac{\pi }{3} \right)\ cm$và ${{x}_{2}}=4\text{cos}\left( 10\pi t+\dfrac{\pi }{6} \right)\ cm$. Phương trình của dao động tổng hợp là
[A]. $x=4\sqrt{2}\text{cos}\left( 10\pi t-\dfrac{\pi }{12} \right)\ cm$
[B]. $x=8\text{cos}\left( 10\pi t-\dfrac{\pi }{12} \right)\ cm$
[C]. $x=8\text{cos}\left( 10\pi t-\dfrac{\pi }{6} \right)\ cm$
[D]. $x=4\sqrt{2}\text{cos}\left( 10\pi t-\dfrac{\pi }{6} \right)\ cm$
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $4\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }4\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}4\sqrt{2}\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{12}$
Câu 23.
Dao động tổng hợp của hai dao động điều hoà cùng phương có phương trình dao động lần lượt là \[{{x}_{1}}=4\sqrt{2}c\text{os}\left( 10\pi t+\dfrac{\pi }{3} \right)\ cm,\ {{x}_{2}}=4\sqrt{2}c\text{os}\left( 10\pi t-\dfrac{\pi }{6} \right)\ cm\] có phương trình
[A]. $x=8\text{cos}\left( 10\pi t-\dfrac{\pi }{6} \right)\ cm$
[B]. \[x=4\sqrt{2}\text{cos}\left( 10\pi t-\dfrac{\pi }{6} \right)\ cm\]
[C]. $x=4\sqrt{2}\text{cos}\left( 10\pi t+\dfrac{\pi }{12} \right)\ cm$
[D]. $x=8\text{cos}\left( 10\pi t+\dfrac{\pi }{12} \right)\ cm$
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $4\sqrt{2}\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }4\sqrt{2}\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}8\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{12}$
Câu 24.
Một vật tham gia đồng thời hai dao động cùng phương cùng tần số. Dao động thành phần thứ nhất có biên độ là 5 cm pha ban đầu là \[\dfrac{\pi }{6}\], dao động tổng hợp có biên độ là 10cm pha ban đầu là \[\dfrac{\pi }{2}\]. Dao động thành phần còn lại có biên độ và pha ban đầu là:
[A]. Biên độ là 10 cm, pha ban đầu là \[\dfrac{\pi }{2}\].
[B]. Biên độ là $5\sqrt{3}$ cm, pha ban đầu là $\dfrac{\pi }{3}$
[C]. Biên độ là $5$ cm, pha ban đầu là $\dfrac{2\pi }{3}$.
[D]. Biên độ là $5\sqrt{3}$ cm, pha ban đầu là $\dfrac{2\pi }{3}$
Ta có: \[{{x}_{1}}=x-{{x}_{2}}\]
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $10\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{2}-\text{ }\!\!~\!\!\text{ }5\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}5\sqrt{3}\angle \dfrac{\text{2 }\!\!\pi\!\!\text{ }}{3}$
Câu 25.
Cho hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ A và có pha ban đầu là \[-\dfrac{\pi }{4}rad\]và \[\dfrac{\pi }{4}rad\]. Biên độ và pha ban đầu của dao động tổng hợp hai dao động trên lần lượt là
[A]. \[A\sqrt{2}\] và 0 rad.
[B]. 0 và \[\pi \] rad.
[C]. 2A và \[\dfrac{\pi }{2}rad\].
[D]. \[\dfrac{A\sqrt{2}}{2}\]và 0 rad.
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $1\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{4}+\text{ }\!\!~\!\!\text{ }1\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{4}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}\sqrt{2}\angle 0$
Câu 26.
Cho hai dao động điều hoà cùng phương, cùng tần số, cùng biên độ \[\sqrt{2}\ cm\] và có các pha ban đầu lần lượt là \[\dfrac{2\pi }{3}\] và \[\dfrac{\pi }{6}\]. Pha ban đầu và biên độ của dao động tổng hợp của hai dao động trên là
[A]. \[\varphi =\dfrac{5\pi }{12}\ rad,\ A=2\ cm.\]
[B]. \[\varphi =\dfrac{5\pi }{12}\ rad,\ A=2\ cm.\]
[C]. \[\varphi =\dfrac{\pi }{4}\ rad,\ A=2\sqrt{2}\ cm.\]
[D]. \[\varphi =\dfrac{\pi }{2}\ rad,\ A=2\ cm.\]
+ Đặt máy ở chế độ số phức CMPLX (mode 2)
+ Đưa máy về chế độ Rad (shift mode 4)
+ Nhập: $\sqrt{2}\angle \dfrac{\text{2 }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }\sqrt{2}\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}2\angle \dfrac{5\pi }{12}$
Câu 27.
Có 2 dao động điều hoà cùng phương, cùng tần số có phương trình $x_{1}$ = 3sin(ωt – 0,5π) cm; $x_{2}$ = 4cos(ωt) cm. Dao động tổng hợp của 2 dao động trên
[A]. có biên độ 7 cm
[B]. có biên độ 1 cm
[C]. ngược pha với $x_{2}$.
[D]. cùng pha với $x_{1}$
\[{{x}_{1}}=3sin\left( \omega t-0,5\pi \right)cm=3cos\left( \omega t-0,5\pi -0,5\pi \right)=3cos\left( \omega t-\pi \right)\]
\[{{x}_{2}}=4cos\left( \omega t \right)\]
Hai dao động ngược pha nhau nên: \[A=\left| {{A}_{1}}-{{A}_{2}} \right|=4-3=1cm\]
Câu 28.
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình lần lượt là $x_{1}$ = 6sin(πt + \[{\varphi _1}\]) cm và $x_{2}$ = 8cos(πt +$\dfrac{\pi }{3}$) cm. Biên độ dao động tổng hợp có giá trị A = 14 cm thì pha ban đầu của dao động thứ nhất là
[A]. π/6 rad
[B]. 2π/3 rad
[C]. 5π/6 rad
[D]. π/3 rad
Nhận thấy 6 + 8 = 14 → \[A={{A}_{1}}+{{A}_{2}}\] → Hai dao động cùng pha
x2 = 8cos(πt +$\dfrac{\pi }{3}$) = 8sin(πt +$\dfrac{\pi }{3}$+$\dfrac{\pi }{2}$) = 8sin(πt +$\dfrac{5\pi }{6}$)
Câu 29.
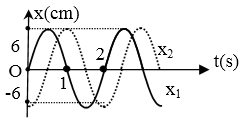
Cho 2 dao động điều hoà $x_{1}$ và $x_{2}$ cùng phương, cùng tần số có đồ thị như hình vẽ. Dao động tổng hợp của $x_{1}$ và $x_{2}$ có phương trình :
[A]. x = 0
[B]. \[x=6\sqrt{2}c\text{os}(\pi t-\dfrac{\pi }{4})(cm)\]
[C]. \[x=6\sqrt{2}c\text{os}(\pi t+\dfrac{\pi }{4})(cm)\]
[D]. \[x=6\sqrt{2}c\text{os}(\pi t-\dfrac{3\pi }{4})(cm)\]
Từ đồ thị ta được: $\left\{ \begin{array}{l}{x_1} = 6\cos (\pi t – \dfrac{\pi }{2})\\{x_2} = 6\cos (\pi t – \pi )\end{array} \right.$
+ Nhập: $6\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!~\!\!\text{ }6\angle -\pi \text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}6\sqrt{2}\angle -\dfrac{3\pi }{4}$
Câu 30.
Hai dao động điều hòa (1) và (2) cùng phương, cùng tần số và cùng biên độ A = 4cm. Tại một thời điểm nào đó, dao động (1) có li độ x = 2$\sqrt{3}$ cm, đang chuyển động ngược chiều dương, còn dao động (2) đi qua vị trí cân bằng theo chiều dương. Lúc đó, dao động tổng hợp của hai dao động trên có li độ bao nhiêu và đang chuyển động theo hướng nào?
[A]. x = 8cm và chuyển động ngược chiều dương
[B]. x = 0 và chuyển động ngược chiều dương
[C]. x = 4$\sqrt{3}$cm và chuyển động theo chiều dương
[D]. x = 2$\sqrt{3}$cm và chuyển động theo chiều dương.
+ $\left\{ \begin{array}{l}{x_1} = 2\sqrt 3 \\{v_1} < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c{\rm{os}}{\varphi _1} = \dfrac{{\sqrt 3 }}{2}\\{\varphi _1} > 0\end{array} \right. \Rightarrow {\varphi _1} = \dfrac{\pi }{6}$
+ $\left\{ \begin{array}{l}{x_2} = 0\\{v_2} > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c{\rm{os}}{\varphi _2} = 0\\{\varphi _2} < 0\end{array} \right. \Rightarrow {\varphi _1} = – \dfrac{\pi }{2}$
+ Nhập: $4\angle \dfrac{{\rm{\pi }}}{6} + {\rm{\;}}4\angle – \dfrac{\pi }{2}{\rm{\;}}4\angle – \dfrac{\pi }{6} \to \left\{ \begin{array}{l}x = 4\cos \left( { – \dfrac{\pi }{6}} \right) = 2\sqrt 3 \\v > 0\end{array} \right.$.
Câu 31.
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình là $x_{1}$ = 3sin(10t – \[\dfrac{\pi }{3}\]) cm và $x_{2}$ = 4cos(10t + \[\dfrac{\pi }{6}\]) cm. Tốc độ cực đại của vật là
[A]. v = 70 cm/s
[B]. v = 50 cm/s
[C]. v = 5 m/s
[D]. v = 10 cm/s
x1 = 3sin(10t – \[\dfrac{\pi }{3}\]) cm = 3cos(10t – \[\dfrac{5\pi }{6}\]) cm
+ Nhập: $3\angle -\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!~\!\!\text{ }4\angle \dfrac{\pi }{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}1\angle \dfrac{\pi }{6}$
+ Vmax = A.ω = 1.10 = 10 cm/s
Câu 32.
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình dao động lần lượt là ${{x}_{1}}={{A}_{1}}c\text{os}\left( 10t-\dfrac{\pi }{6} \right)cm;\ {{x}_{2}}=3c\text{os}\left( 10t-\dfrac{5\pi }{6} \right)cm$. Vật dao động có tốc độ cực đại là 70 cm/s. Biên độ dao động $A_{1}$ có giá trị là
[A]. 4 cm
[B]. 3 cm.
[C]. 5 cm.
[D]. 8 cm.
+ Vmax = A.ω = A.10 = 70 cm/s → A = 7 cm
Biên độ của dao động tổng hợp được xác định:
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {7^2} = A_1^2 + {3^2} + 2A_1^{}.3.{\rm{cos}}\left( { – \dfrac{\pi }{6} + \dfrac{{5\pi }}{6}} \right)\\ \Leftrightarrow A_1^2 – 3A_1^{} – 40 = 0 \Rightarrow A_1^{} = 8cm \end{array}\]
Câu 33.
Một vật có khối lượng m = 0,5 kg thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số góc 4π rad/s, ${{x}_{1}}={{A}_{1}}c\text{os}\left( \omega t+\dfrac{\pi }{6} \right)cm$, ${{x}_{2}}=4\sin \left( \omega t-\dfrac{\pi }{3} \right)cm$. Lấy \[{\pi ^2}\] =10. Biết độ lớn cực đại của lực hồi phục tác dụng lên vật trong quá trình vật dao động là 2,4 N. Biên độ $A_{1}$ của dao động $x_{1}$ là
[A]. 7 cm.
[B]. 6 cm.
[C]. 5 cm.
[D]. 3 cm.
${{x}_{2}}=4\sin \left( \omega t-\dfrac{\pi }{3} \right)=4c\text{os}\left( \omega t-\dfrac{5\pi }{6} \right)cm$
+ Lực phục hồi cực đại: \[{{F}_{max}}=m.{{\omega }^{2}}.A=2,4\Rightarrow 0,5.{{(4\pi )}^{2}}.A=2,4\Rightarrow A=0,03m=3cm.\]
+ Độ lệch pha giữa hai dao động là: \[\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\dfrac{\pi }{6}+\dfrac{5\pi }{6}=\pi \]
→ Hai dao động ngược pha
+ \[A=\left| {{A}_{1}}-{{A}_{2}} \right|=3cm\Rightarrow {{A}_{1}}=7cm\]
Câu 34.
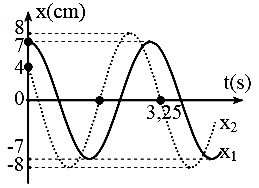
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có đồ thị như hình vẽ.
Độ lớn gia tốc cực đại của vật là
[A]. 7,51 $cm/s^2$.
[B]. 27,23 $cm/s^2$
[C]. 57,02 $cm/s^2$
[D]. 75,1 $cm/s^2$
+ Từ đồ thị của x1 ta có: $\dfrac{T}{12}+T=3,25\Rightarrow \omega =\dfrac{2\pi }{3}$
+ Ta có: ${{x}_{1}}=7\angle 0,\text{ }{{x}_{2}}=8\angle \dfrac{\pi }{3}$$\to x\text{ }=\text{ }13\angle 0,56$
Gia tốc cực đại: \[{{a}_{max}}={{\omega }^{2}}.A\text{ }={{\left( \dfrac{2\pi }{3} \right)}^{2}}.13\approx 57\left( cm/{{s}^{2}} \right)\]
Câu 35.
Vật khối lượng 2 kg, thực hiện đồng thời hai dao động điều hoà cùng phương, các dao động thành phần có biểu thức $x_{1}$= 3cos(2πt +$\dfrac{\pi }{3}$) cm, $x_{2}$ = 4cos(2πt -$\dfrac{\pi }{6}$) cm. Cơ năng dao động của vật là
[A]. 4,0J
[B]. 0,01J
[C]. 0,1J
[D]. 0,4J
+ Nhập: $3\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}+\text{ }\!\!~\!\!\text{ }4\angle -\dfrac{\pi }{6}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}5\angle 0,12$ → A = 5 cm = 0,05 m.
Cơ năng dao động: \[\text{W}=\dfrac{1}{2}m{{\omega }^{2}}.{{A}^{2}}=\dfrac{1}{2}.2{{\left( 2\pi \right)}^{2}}{{.0,05}^{2}}=0,1J\]
Câu 36.
Dao động của một chất điểm là tổng hợp của hai dao động điều hoà cùng phương, có phương trình lần lượt là $x_{1}$ = 6cos(10t + \[\dfrac{5\pi }{6}\]) cm và $x_{2}$ = 6cos(–10t + 0,5π) cm (t tính bằng s). Gia tốc cực đại của vật bằng
[A]. 4\[\sqrt{3}\] $m/s^2$.
[B]. 6\[\sqrt{3}\] $m/s^2$.
[C]. 6,0 $m/s^2$..
[D]. 12 $m/s^2$.
\[{{x}_{2}}=6cos\left( 10t+0,5\pi \right)cm=6cos\left( 10t0,5\pi \right)cm\]
+ Nhập: $6\angle \dfrac{\text{5 }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!~\!\!\text{ }6\angle -\dfrac{\pi }{2}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}6\angle -\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{6}$ → A = 6 cm = 0,06 m
Gia tốc cực đại: \[{{a}_{max}}={{\omega }^{2}}.A=\] ${{\left( 10 \right)}^{2}}.0,06=6\left( m/{{s}^{2}} \right)$
Câu 37.
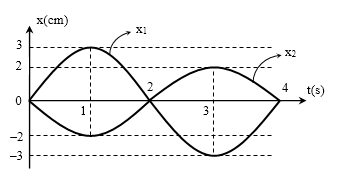
Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau: Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:
[A]. \[x=5cos\dfrac{\pi }{2}t\](cm)
[B]. \[x=\cos \left( \dfrac{\pi }{2}t-\dfrac{\pi }{2} \right)\](cm)
[C]. \[x=\cos \left( \dfrac{\pi }{2}t-\dfrac{\pi }{2} \right)\](cm)
[D]. \[x=\cos \left( \dfrac{\pi }{2}t-\pi \right)\](cm)
T = 4s → $\omega =\dfrac{\pi }{2}$
+ Phương trình (1) là: ${{x}_{1}}=3\cos \left( \dfrac{\pi }{2}t-\dfrac{\pi }{2} \right)$
+ Phương trình (2) là: ${{x}_{2}}=2\cos \left( \dfrac{\pi }{2}t+\dfrac{\pi }{2} \right)$
Do x1 và x2 ngược pha nhau, và \[{{A}_{1}}>{{A}_{2}}\] nên: A = 3 – 2 = 1 cm
Phương trình dao động tổng hợp là: $x=\cos \left( \dfrac{\pi }{2}t-\dfrac{\pi }{2} \right)$
Câu 38.
Cho hai dao động điều hòa cùng phương cùng chu kì 2 s. Dao động thứ nhất tại thời điểm t = 0 có li độ bằng biên độ và bằng 1 cm. Dao động thứ hai có biên độ bằng$\sqrt{3}\,cm$, tại thời điểm ban đầu có li độ bằng 0 và vận tốc có giá trị âm. Biên độ dao động tổng hợp của hai dao động trên là
[A]. 2 cm
[B]. 3 cm.
[C]. 5 cm
[D]. \[2\sqrt{3}\,cm.\]
\[T=2s\to \omega =\pi \left( rad/s \right)\]
+ Phương trình (1) là: ${{x}_{1}}=\cos \pi t$
+ Phương trình (2) là: ${{x}_{2}}=\sqrt{3}\cos \left( \pi t+\dfrac{\pi }{2} \right)$
+ Nhập: \[1\angle 0+\text{ }\!\!~\!\!\text{ }\sqrt{3}\angle \dfrac{\pi }{2}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}2\angle \dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}\] → A = 2 cm
Câu 39.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: \[{{x}_{1}}=4\sqrt{3}\cos \left( 10\pi t \right)\,\,cm\]và $x_{2}$ = 4sin(10πt) cm. Tốc độ của của chất điểm ở thời điểm t = 2 s là
[A]. 125cm/s
[B]. 120,5 cm/s
[C]. –125 cm/s
[D]. 125,7 cm/s
\[{{x}_{1}}=4\sqrt{3}\cos \left( 10\pi t \right)\,\,cm\]
x2 = 4sin(10πt) cm = 4cos(10πt $-\dfrac{\pi }{2}$) cm.
+ Nhập: \[4\sqrt{3}\angle 0+\text{ }\!\!~\!\!\text{ }4\angle -\dfrac{\pi }{2}\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}8\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{6}\]
\[\begin{array}{l} x = 8\cos \left( {10\pi t – \dfrac{\pi }{6}} \right)\,\,cm\\ \Rightarrow v = – 80\pi sin\left( {10\pi t – \dfrac{\pi }{6}} \right)\,\,cm\\ t = 2 \to \left| v \right| = 40\pi \approx 125,7cm/s \end{array}\]
Câu 40.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: $x_{1}$ = $\sqrt{3}$cos(10πt + 0,5π) cm; $x_{2}$ = cos(10πt + π) cm. Tốc độ trung bình của vật trong một chu kỳ dao động là
[A]. 40 cm/s.
[B]. 4 cm/s.
[C]. 40 m/s.
[D]. 4 m/s.
+ Nhập: \[\sqrt{3}\angle \dfrac{\pi }{2}+\text{ }\!\!~\!\!\text{ }1\angle \pi \text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}2\angle \dfrac{\text{2 }\!\!\pi\!\!\text{ }}{3}\]
+ Tốc độ trung bình của vật trong 1 chu kì là: $\overline{v}=\dfrac{4A}{T}=\dfrac{4.2}{0,2}=40\left( cm/s \right)$
Câu 41.
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là $x_{1}$ = $A_{1}$cos(20πt – 0,25π) cm và $x_{2}$ = 6cos(20πt + 0,5π) cm. Biết phương trình dao động tổng hợp là x = 6cos(20πt+φ) cm. Biên độ $A_{1}$ là:
[A]. 12 cm
[B]. $6\sqrt{2}$ cm
[C]. $6\sqrt{3}$ cm
[D]. 6 cm
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {6^2} = A_1^2 + {6^2} + 2A_1^{}.6.{\rm{cos}}\left( { – 0,25\pi – 0,5\pi } \right)\\ \Leftrightarrow A_1^2 – 6\sqrt 2 A_1^{} = 0 \Rightarrow A_1^{} = 6\sqrt 2 cm \end{array}\]
Câu 42.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: $x_{1}$ =$\sqrt{3}$cos(20πt – 0,5π) cm; $x_{2}$ = cos(20πt) cm. Xác định thời điểm đầu tiên vật qua li độ x = -1 cm theo chiều dương.
[A]. 1/6 s
[B]. 1/12 s
[C]. 1/4 s
[D]. 1/8 s
+ Nhập: \[\sqrt{3}\angle -\dfrac{\pi }{2}+\text{ }\!\!~\!\!\text{ }1\angle 0\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}2\angle -\dfrac{\text{ }\!\!\pi\!\!\text{ }}{3}\] → $x=2\cos \left( 20\pi t-\dfrac{\pi }{3} \right)$
Từ trục phân bố thời gian ta có:
$\Delta t=\dfrac{T}{6}+\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{5T}{6}=\dfrac{1}{12}$
Câu 43.
Vật nặng khối lượng m thực hiện dao động điều hòa với phương trình $x_{1}$ = $A_{1}$cos(ωt +$\dfrac{\pi }{3}$)cm thì cơ năng là $W_{1}$, khi thực hiện dao động điều hòa với phương trình $x_{2}$ = $A_{2}$cos(ωt )cm thì cơ năng là $W_{2}$ = 4$W_{1}$. Khi vật thực hiện dao động là tổng hợp của hai dao động $x_{1}$ và $x_{2}$ trên thì cơ năng là W. Hệ thức đúng là:
[A]. W = 5$W_{2}$
[B]. W = 3$W_{1}$
[C]. W = 7$W_{1}$
[D]. W = 2,5$W_{1}$
\[{{W}_{2}}=4{{W}_{1}}\to {{A}_{2}}=2{{A}_{1}}.\quad Coi\ {{A}_{1}}=1\to {{A}_{2}}=2\]
+ Nhập: \[1\angle \dfrac{\pi }{3}+\text{ }\!\!~\!\!\text{ }2\angle 0\text{ }\!\!~\!\!\text{ }\xrightarrow{shift\ 2\ 3}\sqrt{7}\angle 0,33\Rightarrow A=\sqrt{7}=\sqrt{7}{{A}_{1}}\Rightarrow \text{W}=7{{W}_{1}}\]
Câu 44.
Hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là: ${{\text{x}}_{\text{1}}}\text{ = 6cos(}\omega \text{t – }\dfrac{\pi }{\text{6}}\text{) (cm)}$ và ${{\text{x}}_{\text{2}}}\text{ = }{{\text{A}}_{\text{2}}}\text{cos(}\omega \text{t + }{{\varphi }_{\text{2}}}\text{)}$(cm). Dao động tổng hợp của hai dao động này có phương trình $\text{x = 6cos(}\omega \text{t + }\dfrac{\pi }{\text{6}}\text{)(cm)}$. Giá trị của ${{\text{A}}_{\text{2}}}$ và ${{\varphi }_{\text{2}}}$ lần lượt là
[A]. $\text{6 cm}$ và $\dfrac{\pi }{\text{3}}$.
[B]. $\text{12 cm}$ và $\dfrac{\pi }{\text{3}}$.
[C]. $\text{6 cm}$ và $\dfrac{\pi }{2}$.
[D]. $\text{12 cm}$ và $\dfrac{\pi }{2}$.
Ta có: \[{{x}_{2}}= x – {{x}_{1}}\]
+ Nhập: \[6\angle \dfrac{\pi }{6}-6\angle -\dfrac{\pi }{6}\xrightarrow{shift\ 2\ 3}6\angle \dfrac{\pi }{2}\]
Câu 45.
Phương trình dao động tổng hợp của hai dao động cùng phương, cùng tần số là: x = 2\[\sqrt{3}\]cos10\[\pi \]t(cm). Một trong hai dao động đó có phương trình $x_{1}$ = 2cos(10\[\pi \]t – \[\dfrac{\pi }{2}\])cm thì phương trình của dao động thứ hai là:
[A]. $x_{2}$ = 2sin(10\[\pi \]t + \[\dfrac{3\pi }{4}\])cm
[B]. $x_{2}$ = 2\[\sqrt{3}\]cos(10\[\pi \]t + \[\dfrac{5\pi }{6}\])cm
[C]. $x_{2}$ = 4cos (10\[\pi \]t + \[\dfrac{\pi }{6}\])cm
[D]. $x_{2}$= 2\[\sqrt{3}\]sin(10\[\pi \]t + \[\dfrac{\pi }{3}\])cm
Ta có: x2 = x – x1
+ Nhập: \[2\sqrt{3}\angle 0-2\angle -\dfrac{\pi }{2}\xrightarrow{shift\ 2\ 3}4\angle \dfrac{\pi }{6}\]
Câu 46.
Một chất điểm có khối lượng 50 g tham gia đồng thời hai dao động điều hoà cùng phương cùng biên độ 10 cm, cùng tần số góc 10 rad/s. Năng lượng của dao động tổng hợp bằng 25 mJ. Độ lệch pha của hai dao động thành phần bằng
[A]. 0 rad
[B]. π/3 rad
[C]. π/2 rad
[D]. 2π/3 rad
+ Ta có: \[\text{W}=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Leftrightarrow {{25.10}^{-3}}=\dfrac{1}{2}{{.50.10}^{-3}}{{.10}^{2}}.{{A}^{2}}\Rightarrow A=0,1m=10cm\]
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\Delta \varphi \Leftrightarrow A_{}^2 = 2A_1^2\left( {1 + {\rm{cos}}\Delta \varphi } \right) \Leftrightarrow {10^2} = {2.10^2}.\left( {1 + {\rm{cos}}\Delta \varphi } \right)\\ \Leftrightarrow {\rm{cos}}\Delta \varphi = – \dfrac{1}{2} \Rightarrow \Delta \varphi = \dfrac{{2\pi }}{3} \end{array}\]
Câu 47.
Một vật thực hiện đồng thời hai dao động điều hoà có phương trình $x_{1}$ = $A_{1}$cos(20t + π/6) cm, $x_{2}$ = 3cos(20t + 5π/6) cm. Biết tốc độ cực đại của vật là 140 cm/s. Khi đó biên độ $A_{1}$ và pha ban đầu của vật là
[A]. $A_{1}$ = 8 cm, φ = $52^{0}$
[B]. $A_{1}$ = 8 cm, φ = – $52^{0}$
[C]. $A_{1}$ = 5 cm, φ = $52^{0}$
[D]. Một giá trị khác.
\[ + {v_{max}} = A\omega = 140 \to A = 7cm\]
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {7^2} = A_1^2 + {3^2} + 2A_1^{}.3.{\rm{cos}}\left( {\dfrac{\pi }{6} – \dfrac{{5\pi }}{6}} \right)\\ \Leftrightarrow A_1^2 – 3A_1^{} – 40 = 0 \Rightarrow A_1^{} = 8cm \end{array}\]
+ Nhập: \[8\angle \dfrac{\pi }{6}+3\angle \dfrac{5\pi }{6}\xrightarrow{shift\ 2\ 3}7\angle 0,9rad={{52}^{0}}\]
Câu 48.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: $x_{1}$ = 3cos(10t + \[\dfrac{\pi }{3}\]) cm, $x_{2}$ = $A_{2}$cos(10t – \[\dfrac{\pi }{6}\]) cm. Tốc độ của vật khi qua vị trí cân bằng là 50 cm/s. Biên độ dao động thành phần thứ hai là
[A]. 1 cm.
[B]. 4 cm
[C]. 2 cm.
[D]. 5 cm.
\[\begin{array}{l} + {\rm{ }}{v_{max}} = {\rm{ }}A\omega = {\rm{ }}50 \Rightarrow A{\rm{ }} = {\rm{ }}5{\rm{ }}cm\\ A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {5^2} = A_2^2 + {3^2} + 2A_2^{}.3.{\rm{cos}}\left( {\dfrac{\pi }{3} + \dfrac{\pi }{6}} \right)\\ \Rightarrow A_2^{} = 4cm \end{array}\]
Câu 49.
Một vật đồng thời tham gia hai dao động điều hoà cùng phương cùng tần số góc ω = 20 rad/s. Dao động thành phần thứ nhất có biên độ $A_{1}$ = 6 cm và pha ban đầu \[{\varphi _1}\] = 0,5π, dao động thành phần thứ hai có pha ban đầu \[{\varphi _2}\] = 0. Biết tốc độ cực đại khi vật dao động là 2 m/s. Biên độ dao động thành phần thứ hai là
[A]. $A_{2}$ = 10 cm
[B]. $A_{2}$ = 4 cm
[C]. $A_{2}$ = 20 cm
[D]. $A_{2}$ = 8 cm
\[\begin{array}{l} + {\rm{ }}{v_{max}} = A\omega = 200{\rm{ }}cm/s \Leftrightarrow A.20{\rm{ }} = {\rm{ }}200 \Rightarrow A{\rm{ }} = {\rm{ }}10{\rm{ }}cm\\ A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {10^2} = A_2^2 + {6^2} + 2A_2^{}.6.{\rm{cos}}\left( {0,5\pi } \right)\\ \Rightarrow A_2^{} = 8cm \end{array}\]
Câu 50.
Một vật khối lượng m = 100g thực hiện dao động tổng hợp của hai dao động điều hòa cùng phương, có phương trình dao động là ${{x}_{1}}=5\cos (10t+\pi )\text{ }cm;\text{ }{{x}_{2}}=10\cos \left( 10t-\dfrac{\pi }{3} \right)cm$. Giá trị của lực kéo về tác dụng lên vật cực đại là
[A]. \[50\sqrt{3}\]N
[B]. \[50\sqrt{3}\]N
[C]. \[50\sqrt{3}\]N
[D]. 5 N
+ Nhập: \[5\angle \pi +10\angle -\dfrac{\pi }{3}\xrightarrow{shift\ 2\ 3}5\sqrt{3}\angle -\dfrac{\pi }{2}\]
+ Lực kéo về cực đại: \[{{F}_{max}}=m.{{\omega }^{2}}.A=\] ${{0,1.10}^{2}}.0,05\sqrt{3}$ = \[0,5\sqrt{3}\]N
Câu 51.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: $x_{1}$ = $A_{1}$ cos(10t + \[\dfrac{\pi }{6}\] )cm và $x_{2}$ = 10cos(10t + \[\dfrac{2\pi }{3}\]) cm. Biết rằng vận tốc cực đại của vật bằng \[100\sqrt{2}\]cm/s . Biên độ $A_{1}$ có giá trị là:
[A]. $A_{1}$ = 8\[\sqrt{2}\]cm
[B]. $A_{1}$ = 8\[\sqrt{2}\]cm
[C]. $A_{1}$ = 10 cm
[D]. $A_{1}$ = 10\[\sqrt{2}\]cm
\[+\text{ }{{v}_{max}}=\text{ }A\omega =100\sqrt{2}\] cm/s → A.10 = \[100\sqrt{2}\]→ A = \[10\sqrt{2}\] cm
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\left( {{\varphi _2} – {\varphi _1}} \right) \Leftrightarrow {\left( {10\sqrt 2 } \right)^2} = A_1^2 + {10^2} + 2A_1^{}.10.{\rm{cos}}\left( {\dfrac{\pi }{6} – \dfrac{{2\pi }}{3}} \right)\\ \Rightarrow A_1^{} = 10cm \end{array}\]
Câu 52.
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số 10 Hz với các biên độ thành phần là 7 cm và 8 cm. Cho biết hiệu số pha của hai dao động là \[\dfrac{\pi }{3}\]. Vận tốc của vật khi nó qua vị trí có li độ x = 12 cm là
[A]. 314 cm/s.
[B]. 100 cm/s.
[C]. 100 cm/s.
[D]. 120π cm/s.
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\Delta \varphi = {7^2} + {8^2} + 2.7.8.{\rm{cos}}\dfrac{\pi }{3}\\ \Rightarrow A = 13cm\\ v = \omega \sqrt {{A^2} – {x^2}} = 2\pi .10\sqrt {{{13}^2} – {{12}^2}} = 100\pi \left( {cm/s} \right) = 314\left( {cm/s} \right) \end{array}\]
Câu 53.
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là: $x_{1}$ = 3cos(4t + 0,5π) cm và $x_{2}$ = $A_{2}$cos(4t). Biết khi động năng của vật bằng \[\dfrac{1}{3}\] cơ năng của vật thì vật có tốc độ 8\[\sqrt{3}\] cm/s. Biên độ $A_{2}$ bằng
[A]. 1,5 cm.
[B]. 3 cm.
[C]. 3\[\sqrt{2}\] cm.
[D]. 3\[\sqrt{2}\] cm.
\[\begin{array}{l} {{\rm{W}}_d} = \dfrac{1}{3}{\rm{W}} \Rightarrow {v^2} = \dfrac{1}{3}v_{{\rm{max}}}^2 \Rightarrow v_{{\rm{max}}}^{} = v\sqrt 3 = 8\sqrt 3 .\sqrt 3 \Rightarrow {v_{m{\rm{ax}}}} = 24\left( {cm/s} \right)\\ + {\rm{ }}{v_{max}} = {\rm{ }}A\omega = {\rm{ }}24{\rm{ }}cm/s \Leftrightarrow A.4{\rm{ }} = {\rm{ }}24 \Rightarrow A{\rm{ }} = {\rm{ }}6{\rm{ }}cm\\ A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\Delta \varphi \Leftrightarrow {6^2} = {3^2} + A_2^2 + 2.3.A_2^{}{\rm{.cos}}0,5\pi \\ \Rightarrow {A_2} = 3\sqrt 3 cm \end{array}\]
Câu 54.
Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương với ${{x}_{1}}=4\cos \left( 5\sqrt{2}t-\dfrac{\pi }{2} \right)cm$ và ${{x}_{2}}={{A}_{2}}\cos \left( 5\sqrt{2}t+\pi \right)cm$. Biết độ lớn vận tốc của vật tại thời điểm động năng bằng thế năng là 40 cm/s. Biên độ dao động thành phần $A_{2}$ là
[A]. 4 cm
[B]. $4\sqrt{2}$cm.
[C]. $\sqrt{3}$cm.
[D]. $4\sqrt{3}$cm
\[{{\text{W}}_{d}}={{\text{W}}_{t}}\Rightarrow {{\text{W}}_{d}}=\dfrac{1}{2}\text{W}\Rightarrow {{v}^{2}}=\dfrac{1}{2}v_{\text{max}}^{2}\Rightarrow v_{\text{max}}^{{}}=v\sqrt{2}=40\sqrt{2}\Rightarrow {{v}_{m\text{ax}}}=40\sqrt{2}\left( cm/s \right)\]
\[+{{v}_{max}}=A\omega =40\sqrt{2}\]cm/s → A. $5\sqrt{2}$ = $40\sqrt{2}$→ A = 8 cm
\[\begin{array}{l} A_{}^2 = A_1^2 + A_2^2 + 2A_1^{}A_2^{}{\rm{cos}}\Delta \varphi \Leftrightarrow {8^2} = {4^2} + A_2^2 + 2.3.A_2^{}{\rm{.cos}}\left( { – \dfrac{\pi }{2} – \pi } \right)\\ \Rightarrow {A_2} = 4\sqrt 3 cm \end{array}\]
Câu 55.
Cho hai dao động điều cùng phương cùng tần số góc có phương trình lần lượt là $x_{1}$ = 2cos(πt + π/2) cm; $x_{2}$ = 2cos(πt – π) cm. Một vật thực hiện đồng thời hai dao động trên. Xác định thời điểm vật qua li độ $x=2\sqrt{2}$cm lần thứ 100.
[A]. 19,85 s
[B]. 1,985 s
[C]. 199,25 s
[D]. 1985 s
+ Nhập: \[2\angle \dfrac{\pi }{2}+2\angle -\pi \xrightarrow{shift\ 2\ 3}2\sqrt{2}\angle \dfrac{3\pi }{4}\]
Tại t = 0, \[x=2\sqrt{2}\text{cos}\left( \dfrac{3\pi }{4} \right)=-\sqrt{2}\]
+ Vật qua li độ $x=2\sqrt{2}$cm lần đầu tiên là: $\dfrac{T}{8}+\dfrac{T}{2}=\dfrac{5T}{8}$
Trong 1 chu kì vật qua vị trí $x=2\sqrt{2}$ hai lần
+ Thời điểm vật qua li độ $x=2\sqrt{2}$cm lần thứ 100
$t=$99T +$\dfrac{5T}{8}$= 199,25 s
Câu 56.
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số: ${{x}_{1}}=5\cos \left( 10\pi t-\dfrac{\pi }{3} \right)cm$ và ${{x}_{2}}=5\sin \left( 10\pi t+\dfrac{\pi }{2} \right)cm$. Tốc độ trung bình của vật từ lúc bắt đầu chuyển động đến khi qua vị trí cân bằng lần đầu là
[A]. 0,47 m/s.
[B]. 2,47 m/s
[C]. 0,87 m/s.
[D]. 1,47 m/s.
${{x}_{2}}=5\sin \left( 10\pi t+\dfrac{\pi }{2} \right)cm=5\cos (10\pi t).$
Sử dụng máy tính tổng hợp dao động ta được: $x=5\sqrt{3}\cos (10\pi t-\dfrac{\pi }{6})$
Từ lúc bắt đầu chuyển động đến khi qua vị trí cân bằng lần đầu, ta được:
$\left\{ \begin{array}{l} t = \dfrac{{\dfrac{\pi }{2} + \dfrac{\pi }{6}}}{{10\pi }} = \dfrac{1}{{15}}(s)\\ s = A + A[1 – \cos ( – \dfrac{\pi }{6})] \approx 9,8(cm) \end{array} \right. \Rightarrow {v_{tb}} = \dfrac{s}{t} = 147(cm).$