Sự đồng biến và nghịch biến của hàm số (lý thuyết)
Định nghĩa 1.
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và $y=f\left( x \right)$ là một hàm số xác định trên K. Ta nói:
+ Hàm số $y=f\left( x \right)$ được gọi là đồng biến (tăng) trên K nếu
$\forall {{x}_{1}},{{x}_{2}}\in K,{{x}_{1}}<{{x}_{2}}\Rightarrow f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)$
+ Hàm số $y=f\left( x \right)$ được gọi là nghịch biến (giảm) trên K nếu
$\forall {{x}_{1}},{{x}_{2}}\in K,{{x}_{1}}<{{x}_{2}}\Rightarrow f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right)$
Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.
Nhận xét.
Nhận xét 1.
Nếu hàm số $f\left( x \right)$ và $g\left( x \right)$ cùng đồng biến (nghịch biến) trên D thì hàm số $f\left( x \right)+g\left( x \right)$ cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu $f\left( x \right)-g\left( x \right)$.
Nhận xét 2.
Nếu hàm số$f\left( x \right)$ và $g\left( x \right)$ là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số $f\left( x \right).g\left( x \right)$ cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số $f\left( x \right),g\left( x \right)$ không là các hàm số dương trên D.
Nhận xét 3.
Cho hàm số $u=u\left( x \right)$, xác định với $x\in \left( a;b \right)$ và $u\left( x \right)\in \left( c;d \right)$. Hàm số $f\left[ u\left( x \right) \right]$ cũng xác định với $x\in \left( a;b \right)$. Ta có nhận xét sau:
Giả sử hàm số $u=u\left( x \right)$ đồng biến với $x\in \left( a;b \right)$. Khi đó, hàm số $f\left[ u\left( x \right) \right]$ đồng biến với $x\in \left( a;b \right)\Leftrightarrow f\left( u \right)$ đồng biến với $u\in \left( c;d \right)$.
Giả sử hàm số $u=u\left( x \right)$ nghịch biến với $x\in \left( a;b \right)$. Khi đó, hàm số $f\left[ u\left( x \right) \right]$ nghịch biến với $x\in \left( a;b \right)\Leftrightarrow f\left( u \right)$nghịch biến với $u\in \left( c;d \right)$.
Định lí 1.
Giả sử hàm số $f$ có đạo hàm trên khoảng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng K thì $f’\left( x \right)\ge 0,\forall x\in K$.
b) Nếu hàm số nghịch biến trên khoảng K thì $f’\left( x \right)\le 0,\forall x\in K$.
Định lí 2.
Giả sử hàm số $f$ có đạo hàm trên khoảng K. Khi đó:
a) Nếu $f’\left( x \right)>0,\forall x\in K$ thì hàm số $f$ đồng biến trên K.
b) Nếu $f’\left( x \right)<0,\forall x\in K$ thì hàm số $f$ nghịch biến trên K.
c) Nếu $f’\left( x \right)=0,\forall x\in K$ thì hàm số $f$ không đổi trên K.
Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có thêm giả thuyết “ Hàm số liên tục trên đoạn hoặc nửa khoảng đó’. Chẳng hạn:
Nếu hàm số $f$ liên tục trên đoạn $\left[ a;b \right]$ và $f’\left( x \right)>0,\forall x\in \left( a;b \right)$ thì hàm số $f$ đồng biến trên đoạn $\left[ a;b \right]$.
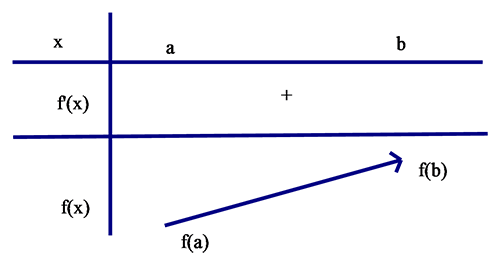
Ta thường biểu diển qua bảng biến thiên như sau:
Định lí 3.(mở rộng của định lí 2)
Giả sử hàm số $f$ có đạo hàm trên khoảng K. Khi đó:
a) Nếu $f’\left( x \right)\ge 0,\forall x\in K$ và $f’\left( x \right)=0$ chỉ tại hữu hạn điểm thuộc K thì hàm số $f$ đồng biến trên K.
b) Nếu $f’\left( x \right)\le 0,\forall x\in K$ và $f’\left( x \right)=0$ chỉ tại hữu hạn điểm thuộc K thì hàm số $f$ đồng biến trên K.