Chuyên đề đồ thị dao động điều hòa, vật lí lớp 12
Câu 1.
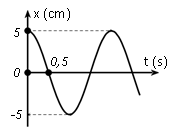
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=5\cos (2\pi t-\dfrac{\pi }{2})cm\]
[B]. \[x=5\cos (\pi t+\dfrac{\pi }{2})cm\]
[C]. \[x=5\cos \pi t\text{ (}cm)\]
[D]. \[x=5\cos (2\pi t+\dfrac{\pi }{2})cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 5 cm.
+) Tại t = 0, vật có x = 5 cm, tức biên dương $\to $ pha ban đầu $\varphi =0$.
+) Từ đồ thị kết hợp với trục phân bố thời gian đã học ta có: $0,5=\dfrac{T}{4}\to T=2\left( s \right)\to \omega =\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=5\cos \pi t\text{ (}cm)\]
Câu 2.
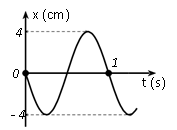
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=4\cos (2\pi t-\dfrac{\pi }{2})cm\]
[B]. \[x=4\cos (\pi t+\dfrac{\pi }{2})cm\]
[C]. \[x=4\cos \pi t\text{ (}cm)\]
[D]. \[x=4\cos (2\pi t+\dfrac{\pi }{2})cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 4 cm.
+) Tại t = 0, vật qua VTCB theo chiều âm $\to $ pha ban đầu $\varphi =\dfrac{\pi }{2}$.
+) Từ đồ thị ta có: $1=T\to \omega =2\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=4\cos (2\pi t+\dfrac{\pi }{2})cm\].
Câu 3.
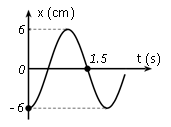
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=6\cos \pi t\text{ (}cm)\]
[B]. \[x=6\cos (2\pi t-\pi )\text{ }cm\]
[C]. \[x=6\cos (\pi t-\pi )\text{ }cm\]
[D]. \[x=6\cos (\dfrac{\pi }{2}t+\pi )\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 6 cm.
+) Tại t = 0, x = – A, biên âm $\to $ pha ban đầu $\varphi =\pm \pi $.
+) Từ đồ thị ta có: $1,5\text{ s}=\dfrac{T}{2}+\dfrac{T}{4}\to T=2\text{ s}\to \omega =\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=6\cos (\pi t-\pi )\text{ }cm\].
Câu 4.
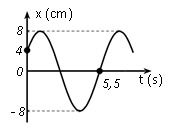
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=8\cos (\dfrac{2\pi }{3}t-\dfrac{\pi }{3})\text{ }cm\]
[B]. \[x=8\cos (\dfrac{\pi }{3}t-\dfrac{\pi }{3})\text{ }cm\]
[C]. \[x=8\cos (\dfrac{\pi }{3}t+\dfrac{2\pi }{3})\text{ }cm\]
[D]. \[x=8\cos (\dfrac{\pi }{3}t+\dfrac{\pi }{3})cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 8 cm.
+) Tại t = 0, vật ở vị trí $x=4=\dfrac{A}{2}$và chuyển động theo chiều dương$\to $ pha ban đầu$\varphi =-\dfrac{\pi }{3}\left( rad \right)$.
+) Từ đồ thị: $5,5=\dfrac{T}{6}+\dfrac{T}{2}+\dfrac{T}{4}\to T=6\left( s \right)\to \omega =\dfrac{\pi }{3}\left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=8\cos (\dfrac{\pi }{3}t-\dfrac{\pi }{3})\text{ }cm\]
Câu 5.
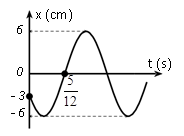
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=6\cos (\pi t+\dfrac{\pi }{3})\text{ }cm\]
[B]. \[x=6\cos (\pi t+\dfrac{2\pi }{3})\text{ }cm\]
[C]. \[x=6\cos (\pi t-\dfrac{\pi }{3})\text{ }cm\]
[D]. \[x=6\cos (2\pi t+\dfrac{2\pi }{3})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 6 cm.
+) Tại t = 0, x = $-\dfrac{A}{2}(-)$\to $ pha ban đầu $\varphi =\dfrac{2\pi }{3}$.
+) Từ đồ thị : $\dfrac{5}{12}\text{ s}=\dfrac{T}{6}+\dfrac{T}{4}\to T=1\text{ s}\to \omega =2\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=6\cos (2\pi t+\dfrac{2\pi }{3})\text{ }cm\]
Câu 6.
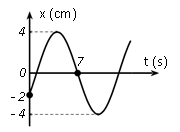
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=4\cos (\dfrac{\pi }{6}t+\dfrac{2\pi }{3})\text{ }cm\]
[B]. \[x=4\cos (\dfrac{\pi }{6}t-\dfrac{2\pi }{3})\text{ }cm\]
[C]. \[x=4\cos (\dfrac{\pi }{3}t-\dfrac{2\pi }{3})\text{ }cm\]
[D]. \[x=4\cos (\dfrac{\pi }{6}t-\dfrac{\pi }{3})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 4 cm.
+) Tại t = 0, x = $-\dfrac{A}{2}(+)$\to $ pha ban đầu $\varphi =-\dfrac{2\pi }{3}$.
+) Từ đồ thị: $7\text{ s}=\dfrac{T}{12}+\dfrac{T}{2}\to T=12\text{ s}\to \omega =\dfrac{\pi }{6}\left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=4\cos (\dfrac{\pi }{6}t-\dfrac{2\pi }{3})\text{ }cm\]
Câu 7.
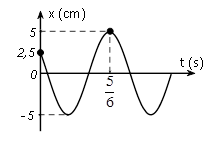
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=5\cos (2\pi t+\dfrac{\pi }{3})\text{ }cm\]
[B]. \[x=5\cos (2\pi t+\dfrac{2\pi }{3})\text{ }cm\]
[C]. \[x=5\cos (\pi t-\dfrac{\pi }{3})\text{ }cm\]
[D]. \[x=5\cos (\pi t-\dfrac{2\pi }{3})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 5 cm.
+) Tại t = 0, x = $\dfrac{A}{2}(-)$\to $ pha ban đầu $\varphi =\dfrac{\pi }{3}$.
+) Từ đồ thị: $\dfrac{5}{6}\text{ s}=\dfrac{T}{12}+\dfrac{T}{4}+\dfrac{T}{2}\to T=1\text{ s}\to \omega =2\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=5\cos (2\pi t+\dfrac{\pi }{3})\text{ }cm\].
Câu 8.
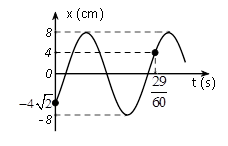
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=8\cos (2\pi t+\dfrac{3\pi }{4})\text{ }cm\]
[B]. \[x = 8\cos (3\pi t + \dfrac{\pi }{4}){\rm{ }}cm\]
[C]. \[x=8\cos (5\pi t-\dfrac{3\pi }{4})\text{ }cm\]
[D]. \[x = 8\cos (2\pi t – \dfrac{{3\pi }}{4}){\rm{ }}cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Biên độ A = 8 cm.
+) Tại t = 0, x = $-\dfrac{A\sqrt{2}}{2}(+)$\to $ pha ban đầu $\varphi =-\dfrac{3\pi }{4}$.
+) Từ đồ thị : $\dfrac{29}{60}\text{ s}=\dfrac{T}{8}+T+\dfrac{T}{12}\to T=0,4\text{ s}\to \omega =5\pi \left( rad/s \right)$
Vậy phương trình dao động cần tìm là \[x=8\cos (5\pi t-\dfrac{3\pi }{4})\text{ }cm\].
Câu 9.
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=10\cos (\dfrac{\pi }{3}t-\dfrac{\pi }{3})\text{ }cm\]
[B]. \[x=10\cos (\dfrac{2\pi }{3}t-\dfrac{\pi }{3})\text{ }cm\]
[C]. \[x=10\cos (\dfrac{2\pi }{3}t+\dfrac{\pi }{3})\text{ }cm\]
[D]. \[x=10\cos (\dfrac{2\pi }{3}t+\dfrac{2\pi }{3})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$(*)
Từ đồ thị ta có:
+) Biên độ A = 8 cm.
+) t2 – t1 = $4,25-2,75=\dfrac{T}{4}+\dfrac{T}{4}\to T=3\left( s \right)\to \omega =\dfrac{2\pi }{3}\left( rad/s \right)$
+) Tại t = 2,75 s, vật ở VTCB và chuyển động theo chiều âm $\to $ Pha dao động ${{\phi }_{2,75s}}=\dfrac{\pi }{2}\left( rad \right)$.
Từ (*), ta có ${{\phi }_{2,75s}}=\dfrac{2\pi }{3}.2,75+\varphi =\dfrac{\pi }{2}\to \varphi =-\dfrac{4\pi }{3}\equiv \dfrac{2\pi }{3}\left( rad \right)$.
Vậy phương trình dao động cần tìm là \[x=10\cos (\dfrac{2\pi }{3}t+\dfrac{2\pi }{3})\text{ }cm\]
Câu 10.

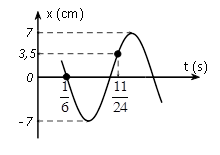
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=7\cos (4\pi t+\dfrac{\pi }{6})\text{ }cm\]
[B]. \[x=7\cos (2\pi t-\dfrac{\pi }{6})\text{ }cm\]
[C]. \[x=7\cos (4\pi t-\dfrac{\pi }{6})\text{ }cm\]
[D]. \[x=7\cos (2\pi t+\dfrac{3\pi }{4})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$(*)
Từ đồ thị ta có:
+) Biên độ A = 7 cm.
+) t2 – t1 = $\dfrac{11}{24}-\dfrac{1}{6}=\dfrac{T}{2}+\dfrac{T}{12}\to T=0,5\left( s \right)\to \omega =4\pi \left( rad/s \right)$
+) Tại t = $\dfrac{1}{6}$ s, vật ở VTCB và chuyển động theo chiều âm $\to $ pha dao động ${{\phi }_{\dfrac{1}{6}s}}=\dfrac{\pi }{2}\left( rad \right)$.
Từ (*), ta có ${{\phi }_{\dfrac{1}{6}s}}=4\pi .\dfrac{1}{6}+\varphi =\dfrac{\pi }{2}\to \varphi =-\dfrac{\pi }{6}\left( rad \right)$.
Vậy phương trình dao động cần tìm là \[x=7\cos (4\pi t-\dfrac{\pi }{6})\text{ }cm\].
Câu 11.
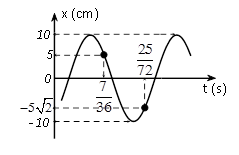
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. \[x=10\cos (4\pi t-\dfrac{\pi }{4})\text{ }cm\]
[B]. \[x=10\cos (6\pi t-\dfrac{3\pi }{4})\text{ }cm\]
[C]. \[x=10\cos (4\pi t+\dfrac{\pi }{4})\text{ }cm\]
[D]. \[x=10\cos (6\pi t-\dfrac{5\pi }{6})\text{ }cm\]
Phương trình dao động có dạng tổng quát là: $x=\text{Acos}(\omega t+\varphi )$(*)
Từ đồ thị ta có:
+) Biên độ A = 10 cm.
+) t2 – t1 = $\dfrac{25}{72}-\dfrac{7}{36}=\dfrac{T}{12}+\dfrac{T}{4}+\dfrac{T}{8}\to T=\dfrac{1}{3}\left( s \right)\to \omega =6\pi \left( rad/s \right)$
+) Tại t = $\dfrac{7}{36}$ s, $x=\dfrac{A}{2}(-)$ $\to $ pha dao động ${{\phi }_{\dfrac{7}{36}s}}=\dfrac{\pi }{3}\left( rad \right)$.
Từ (*), ta có ${{\phi }_{\dfrac{7}{36}s}}=6\pi .\dfrac{7}{36}+\varphi =\dfrac{\pi }{3}\to \varphi =-\dfrac{5\pi }{6}\left( rad \right)$.
Vậy phương trình dao động cần tìm là \[x=10\cos (6\pi t-\dfrac{5\pi }{6})\text{ }cm\].
Câu 12.
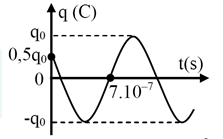
Đồ thị biểu diễn sự phụ thuộc vào thời gian của điện tích ở một bản tụ điện trong mạch dao động LC lí tưởng có dạng như hình vẽ. Phương trình dao động của điện tích ở bản tụ điện này là
[A]. $q={{q}_{0}}c\text{os}\left( \dfrac{{{10}^{7}}\pi }{6}t+\dfrac{\pi }{3} \right)$
[B]. $q={{q}_{0}}c\text{os}\left( \dfrac{{{10}^{7}}\pi }{3}t-\dfrac{\pi }{3} \right)$
[C]. $q={{q}_{0}}c\text{os}\left( \dfrac{{{10}^{7}}\pi }{6}t-\dfrac{\pi }{3} \right)$
[D]. $q={{q}_{0}}c\text{os}\left( \dfrac{{{10}^{7}}\pi }{3}t+\dfrac{\pi }{3} \right)$
Phương trình dao động của điện tích $q={{q}_{0}}\text{cos}(\omega t+\varphi )$
Từ đồ thị ta có:
+) Tại t = 0, q = $\dfrac{{{q}_{0}}}{2}(-)$ $\to $ pha ban đầu $\varphi =\dfrac{\pi }{3}$.
+) Từ đồ thị:
${{7.10}^{-7}}\text{ s}=\dfrac{T}{12}+\dfrac{T}{2}\to T={{12.10}^{-7}}\text{ s}\to \omega =\dfrac{2\pi }{{{12.10}^{-7}}}=\dfrac{\pi }{6}{{.10}^{7}}\left( rad/s \right)$
Vậy phương trình dao động cần tìm là $q={{q}_{0}}c\text{os}\left( \dfrac{{{10}^{7}}\pi }{6}t+\dfrac{\pi }{3} \right)$
Câu 13.
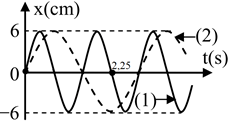
Đồ thị li độ theo thời gian của chất điểm 1 (đường 1) và chất điểm 2 (đường 2) như hình vẽ. Không kể thời điểm t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 5 là
[A]. 3,25 s
[B]. 3,5 s.
[C]. 4,0 s.
[D]. 3,75 s.
Phương trình dao động 2 vật lần lượt là: ${{x}_{1}}={{\text{A}}_{1}}\text{cos}({{\omega }_{1}}t+{{\varphi }_{1}})$
và ${{x}_{1}}={{\text{A}}_{2}}\text{cos}({{\omega }_{2}}t+{{\varphi }_{2}})$
Từ đồ thị dễ thấy:
+) Biên độ A1 = A2 = 6 cm.
+) Tại t = 0, 2 vật cùng qua VTCB theo chiều dương
$\to $ pha ban đầu ${{\varphi }_{1}}={{\varphi }_{2}}=-\dfrac{\pi }{2}$.
+) Từ đồ thị kết hợp với trục phân bố thời gian đã học ta có: T2 = 2T1.
Xét vật dao động (1): ${\rm{2,25 s}} = {T_1} + \dfrac{{{T_1}}}{2} \to {T_1} = 1,5{\rm{ s}} \to {T_2} = 3{\rm{ s}} \to \left\{ \begin{array}{l}{\omega _1} = \dfrac{{4\pi }}{3}\left( {rad/s} \right)\\{\omega _2} = \dfrac{{2\pi }}{3}\left( {rad/s} \right)\end{array} \right.$
Vậy phương trình dao động 2 vật là \[{{x}_{1}}=6\cos (\dfrac{4\pi }{3}t-\dfrac{\pi }{2})\text{ }cm\]và \[{{x}_{2}}=6\cos (\dfrac{2\pi }{3}t-\dfrac{\pi }{2})\text{ }cm\]
Khi hai vật gặp nhau khi x1 = x2
\[6\cos (\dfrac{{4\pi }}{3}t – \dfrac{\pi }{2}){\rm{ = }}6\cos (\dfrac{{2\pi }}{3}t – \dfrac{\pi }{2}){\rm{ }} \to \left[ \begin{array}{l}\dfrac{{4\pi }}{3}t – \dfrac{\pi }{2} = \dfrac{{2\pi }}{3}t – \dfrac{\pi }{2} + 2k\pi ;k \in Z\\\dfrac{{4\pi }}{3}t – \dfrac{\pi }{2} = – \dfrac{{2\pi }}{3}t + \dfrac{\pi }{2} + 2m\pi ;m \in Z\end{array} \right.\]
\[ \to \left[ \begin{array}{l}t = 3k = 3s;{\rm{ 6s; 9s; 12s;}}…\\t = 0,5 + m = 0,5s;{\rm{ 1,5s; 2,5s; 3,5s; }}…\end{array} \right.\]
→ thời điểm lần 5 mà 2 vật gặp nhau là 3,5 s.
Câu 14.
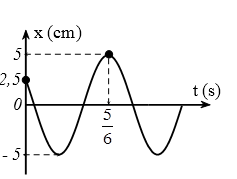
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Từ thời điểm 1,5 s đến thời điểm $\dfrac{1516}{3}$s, vật cách vị trí cân bằng $\dfrac{5\sqrt{3}}{2}$ bao nhiêu lần
[A]. 2013
[B]. 2015
[C]. 2016
[D]. 2014
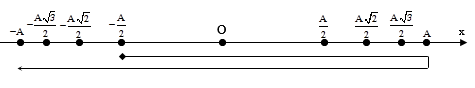
Dễ dàng xác định được phương trình dao động: \[\text{x}=5\cos \left( 2\pi t+\dfrac{\pi }{3} \right)\] cm.
Tại t = 1,5s: ${{\phi }_{1,5s}}=2\pi .1,5+\dfrac{\pi }{3}=\dfrac{10\pi }{3}\equiv -\dfrac{2\pi }{3}$ → \[\text{x}=-\dfrac{A}{2}(+)\]
Khoảng thời gian vật dao động: ∆t = t’ – t = $\dfrac{1516}{3}-1,5=503T+\dfrac{5T}{6}$
Cứ 1 chu kì, vật cách VTCB $\dfrac{5\sqrt{3}}{2}$ cm ($x=\pm \dfrac{A\sqrt{3}}{2}$) 4 lần.
Do đó, kể từ t = 1,5s, sau 503T thì vật cách VTCB $\dfrac{5\sqrt{3}}{2}$ cm 2012 lần và quay lại trạng thái tại t = 1,5s:
\[\text{x}=-\dfrac{A}{2}(+)\], sau đó $\dfrac{5T}{6}$ vật dao động tiếp như sau:
Tức là, vật cách VTCB $\dfrac{5\sqrt{3}}{2}$thêm 3 lần nữa. Vậy tổng là 2015 lần!
Câu 15.
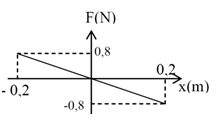
Một vật nhỏ có khối lượng 10 g dao động điều hòa dưới tác dụng của một lực kéo về được chỉ ra trên đồ thị bên. Chu kì dao động của vật là
[A]. 0,256 s
[B]. 0,152 s
[C]. 0,314 s
[D]. 1,255 s
Từ đồ thị: A = 0,2 m; Fmax = mω2A = 0,8 N → ω = 20 rad/s → T = 0,314 s
Câu 16.
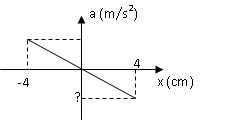
Một vật nhỏ dao động điều hòa với tần số góc 10 rad/s. Giá trị còn thiếu trong dấu ? ở đồ thị hình bên là
[A]. 400
[B]. – 4
[C]. 40
[D]. – 400
amax = ω2A = 400 cm/s2 = 4 m/s2.
Câu 17.
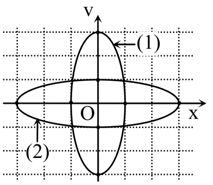
Cho hai vật dao động điều hòa dọc theo hai đường thẳng cùng song song với trục Ox. Vị trí cân bằng của mỗi vật nằm trên đường thẳng vuông góc với trục Ox tại O. Trong hệ trục vuông góc xOv, đường (1) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 1, đường (2) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 2 (hình vẽ). Biết các lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau. Tỉ số giữa khối lượng của vật 2 với khối lượng của vật 1 là
[A]. $\dfrac{1}{3}.$
[B]. 3
[C]. 27
[D]. $\dfrac{1}{{27}}.$
Lực kéo về cực đại bằng nhau, do đó:
${{m}_{1}}\omega _{1}^{2}{{A}_{1}}={{m}_{2}}\omega _{2}^{2}{{A}_{2}}\to \dfrac{{{m}_{2}}}{{{m}_{1}}}=\dfrac{\omega _{1}^{2}{{A}_{1}}}{\omega _{2}^{2}{{A}_{2}}}$
Nhìn đồ thị dễ thấy:
$\dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{1}{3}$ và $\dfrac{{{v}_{1\max }}}{{{v}_{2\max }}}=3\to \dfrac{{{\omega }_{1}}{{A}_{1}}}{{{\omega }_{2}}{{A}_{2}}}=3\to \dfrac{{{\omega }_{1}}}{{{\omega }_{2}}}=9$. Do đó: $\dfrac{{{m}_{1}}}{{{m}_{2}}}=27$.
Câu 18.
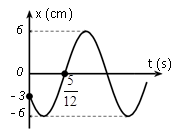
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của vận tốc là
[A]. $v=6\pi \cos (\pi t+\dfrac{\pi }{6})\text{ }cm$
[B]. $v=12\pi \cos (2\pi t-\dfrac{5\pi }{6})\text{ }cm$
[C]. $v=12\pi \cos (\pi t-\dfrac{3\pi }{4})\text{ }cm$
[D]. $v=12\cos (2\pi t+\dfrac{\pi }{3})\text{ }cm$
Đọc đồ thị: $x=6\cos (2\pi t+\dfrac{2\pi }{3})$
$\left. \begin{array}{l}{v_{\max }} = \omega A = 12\pi \\{\rm{ }}{\varphi _v} = \varphi + \dfrac{\pi }{2} = \dfrac{{2\pi }}{3} + \dfrac{\pi }{2} = \dfrac{{7\pi }}{6} \equiv – \dfrac{{5\pi }}{6}\end{array} \right\} \to x = 12\pi \cos (2\pi t – \dfrac{{5\pi }}{6})$ cm/s.
Câu 19.
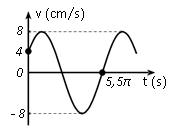
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của vận tốc của vật có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. $x=24\cos (\dfrac{t}{3}-\dfrac{5\pi }{6})\text{ }cm$
[B]. $x=24\cos (\dfrac{t}{3}-\dfrac{2\pi }{3})\text{ }cm$
[C]. $x=8\cos (\dfrac{t}{3}-\dfrac{\pi }{3})\text{ }cm$
[D]. $x=8\cos (\dfrac{\pi }{3}t-\dfrac{\pi }{3})\text{ }cm$
Phương trình vận tốc cần tìm có dạng: $v={{v}_{\max }}\cos \left( \omega t+{{\varphi }_{v}} \right)$
vmax = 8 (cm/s)
Tại t = 0: v = 4 cm = $\dfrac{{{v}_{\max }}}{2}$ và đang tăng → ${{\varphi }_{v}}=-\dfrac{\pi }{3}$
$5,5\pi =\dfrac{T}{6}+\dfrac{T}{2}+\dfrac{T}{4}$ → T = 6π → ω = $\dfrac{1}{3}$ rad/s.
Do đó, $v=8\cos \left( \dfrac{t}{3}-\dfrac{\pi }{3} \right)$ cm/s → $x=24\cos \left( \dfrac{t}{3}-\dfrac{5\pi }{6} \right)$ cm.
Câu 20.
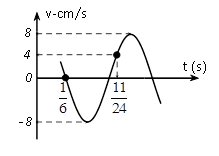
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của vận tốc của vật có dạng như hình vẽ bên. Phương trình dao động của li độ là
[A]. $x=\dfrac{4}{\pi }\cos (\pi t+\dfrac{3\pi }{4})\text{ }cm$
[B]. $x=\dfrac{2}{\pi }\cos (4\pi t-\dfrac{2\pi }{3})\text{ }cm$
[C]. $x=\dfrac{2}{\pi }\cos (2\pi t-\dfrac{\pi }{6})\text{ }cm$
[D]. $x=\dfrac{2}{\pi }\cos (4\pi t+\dfrac{\pi }{6})\text{ }cm$
Phương trình vận tốc cần tìm có dạng: $v={{v}_{\max }}\cos \left( \omega t+{{\varphi }_{v}} \right)$
$\Delta t=\dfrac{11}{24}-\dfrac{1}{6}=\dfrac{T}{4}+\dfrac{T}{3}\to T=0,5\text{s}\to \omega =4\pi $rad/s.
Tại t = $\dfrac{1}{6}$ s: v = 0 (-) → ${{\phi }_{v\left( \dfrac{1}{6}s \right)}}=4\pi .\dfrac{1}{6}+{{\varphi }_{v}}=\dfrac{\pi }{2}\to {{\varphi }_{v}}=-\dfrac{\pi }{6}$
Vậy: $v=8\cos \left( 4\pi t-\dfrac{\pi }{6} \right)$cm/s → $x=\dfrac{2}{\pi }\cos \left( 4\pi t-\dfrac{2\pi }{3} \right)$ cm.
Câu 21.
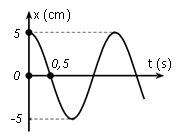
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình vận tốc của vật dao động điều hoà là
[A]. $v=10\pi \cos (2\pi t-\dfrac{\pi }{2})$cm/s
[B]. $v=10\pi \cos (2\pi t+\pi )$cm/s
[C]. $v=5\pi \cos (\pi t+\pi )$cm/s
[D]. $v=5\pi \cos \left( \pi t+\dfrac{\pi }{2} \right)$cm/s
$\left\{ \begin{array}{l}\dfrac{T}{4} = 0,5 \Rightarrow T = 2\left( s \right) \Rightarrow \omega = \pi \left( {ra{\rm{d}}/s} \right)\\A = 5\left( {cm} \right)\end{array} \right.$
→ x = 5cosπt → $v=5\pi \cos \left( \pi t+\dfrac{\pi }{2} \right)$cm/s.