Bài tập bảo toàn cơ năng trường hấp dẫn (hay còn gọi là trường trọng lực) Vật lí lớp 10 khi áp dụng bảo toàn cơ năng chúng ta không quan tâm nhiều đến hình dạng của chuyển động mà chỉ tập trung vào vị trí điểm đầu và điểm cuối trong quá trình chuyển động của vật sau đó so sánh với gốc thế năng để tính toán.
Bảo toàn cơ năng trường hấp dẫn, bài toán con lắc đơn chuyển động trong trường trọng lực chỉ chịu tác dụng của trọng lực.
Con lắc đơn: gồm vật khối lượng m treo vào dây không dãn chiều dài ℓ
Thế năng của con lắc đơn:
Chọn gốc thế năng tại vị trí cân bằng của con lắc đơn (vị trí dây treo hợp với phương thẳng đứng góc 0o)
${{W}_{t}}=mgh=mgl(\cos \alpha -\cos {{\alpha }_{0}})$
Trong đó:
- m: khối lượng vật nặng (kg)
- g: gia tốc rơi tự do (m/s2)
- ℓ: chiều dài dây treo (m)
- α: góc hợp bởi dây treo và phương thẳng đứng
- αo: góc lệch cực đại của dây treo và phương thẳng đứng
Cơ năng của con lắc đơn:
\[W={{W}_{t}}+{{W}_{d}}=mgl(\cos \alpha -\cos {{\alpha }_{0}})+\dfrac{1}{2}m{{v}^{2}}\]
Con lắc đơn chuyển động trong trường trọng lực chỉ chịu tác dụng của trọng lực → cơ năng của con lắc đơn là đại lượng bảo toàn.
Bài tập bảo toàn cơ năng thuộc vật lí lớp 10 chủ đề năng lượng
Bài tập bảo toàn cơ năng của con lắc đơn chuyển động trong trường trọng lực chỉ chịu tác dụng của trọng lực
Bài 1: Con lắc đơn gồm một dây không giãn chiều dài l một đầu gắn cố định, một đầu gắn với vật khối lượng m. Kéo vật m sao cho con lắc đơn hợp với phương thẳng đứng góc αo rồi buông tay.
a/ Xác định vận tốc của con lắc đơn khi dây treo hợp với phương thẳng đứng góc α ≤ αo
b/ Xác định lực căng dây trong trường hợp trên.
Bỏ qua mọi sức cản của môi trường.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
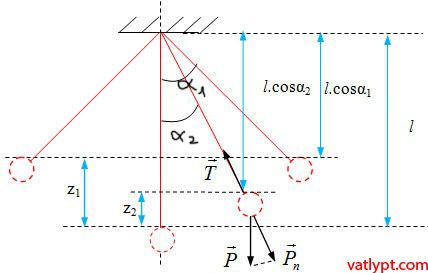
Chọn gốc thế năng tại vị trí cân bằng (α=0)
a/ Thế năng của con lắc đơn tại vị trí bất kỳ
W$_{t}$=mgz2=mg(l – l.cosα)=mgl(1-cosα) =>
(W$_{t}$)max = mgz1= mgl(1-cosαo)
W=W$_{đ}$ + W$_{t}$= (W$_{t}$)max =>
0,5mv2 + mgl(1-cosα) = mgl(1-cosαo)=>
\[v=\sqrt{2gl(cos\alpha -cos\alpha _{o})}\]
b/ Chuyển động của vật m là chuyển động tròn trên bán kính quỹ đạo có bán kính l, hợp giữa lực căng T của dây treo và thành phần P$_{n }$ = mgcosα của trọng lực đóng vai trò lực hướng tâm => áp dụng định luật II Newton ta có
T – mgcosα=m.\[\dfrac{v^{2}}{l}\]=>
T=mgcosα + 2mg(cosα – cosαo) =>
T=mg(3cosα – 2cosαo)
Bài 2: Một con lắc đơn chiều dài l=1,8m, một đầu gắn với vật khối lượng 200g. Thẳng phía dưới điểm treo cách điểm treo một đoạn l/2 có một cái đinh. Kéo vật ra khỏi vị trí cân bằng sao cho dây treo hợp với phương thẳng đứng góc 30o rồi thả nhẹ.
a/ Xác định điểm cao nhất và xác định góc hợp bởi dây dây và phương thẳng đứng sau khi va chạm với đinh.
b/ Khi dây treo quay lại vị trí cân bằng thì dây bị đứt. Tìm hướng và độ lớn vận tốc của vật m lúc sắp chạm đất. Biết rằng điểm treo cách mặt đất 2,3m.
Bỏ qua mọi sức cản và ma sát lấy g=10m/s2.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
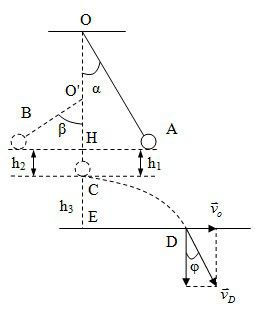
Chọn gốc thế năng tại C (vị trí cân bằng)
áp dụng định luật bảo toàn cơ năng:
W$_{A}$=W$_{B}$ => mgh1=mgh2 => h1=h2=l(1 – cosα)=0,24(m)
\[cos\beta =\dfrac{O’H}{O’B}=\dfrac{l/2 – h_{1}}{l/2}\]
=> β=42,9o
vận tốc tại vị trí cân bằng C:
W$_{B}$=W$_{C}$ => mgh2=0,5mv2 => v=\[\sqrt{2gh_{2}}\]=2,2(m/s)
Khi quay lại C, dây bị đứt chuyển động của vật coi như chuyển động ném ngang với vận tốc ban đầu vo=2,2m/s
Áp dụng định luật bảo toàn cơ năng cho điểm C và D chọn gốc thế năng tại mặt đất.
W$_{C}$=W$_{D}$ => 0,5mvo2 + mgh3=0,5mv$_{D}$2 => v$_{D}$ =7,1(m/s)
hướng của véc tơ vận tốc hợp với phương thẳng đứng góc φ với sinφ=vo/v$_{D}$
Bài 4. Dây treo vật nặng được kéo nghiêng góc bao nhiêu để khi qua vị trí cân bằng lực căng của dây lớn gấp đôi trọng lực của vật nặng.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
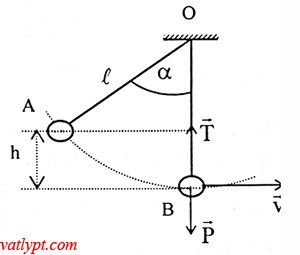
gọi v là vận tốc của vật tại vị trí cân bằng
=> T – mg = ma$_{ht}$ = mv2/L
Để T = 2P = 2mg => T – mg = mg = mv2/L => v2 = gL
bảo toàn cơ năng: 0,5mv2 = mgh = mgL(1-cosα) => α = 60o
Bài 5. Treo vật m = 1kg vào đầu một sợi dây rồi kéo vật khỏi vị trí cân bằng để dây treo hợp với phương thẳng đứng góc αo. Xác định αo để khi buông tay, dây không bị đứt trong quá trình vật chuyển động. Biết dây chịu lực căng tối đa 16N; αo ≤ 90o.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
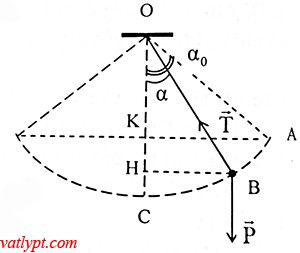
T – mgcosα = ma$_{ht}$ = mv2/L => T = mgcosα + mv2/L
bảo toàn cơ năng
mgho = mgh + 0,5mv2 => mgL(1-cosαo) = mgL(1-cosα) + 0,5mv2
=> v2 = 2gL(cosα – cosαo)
=> T = mg(3cosα – 3cosαo) =>Tmax = mg(3 – cosαo)
Để dây không đứt thì Tmax ≤ 16N => αo ≤ 45o
Bài 6. Quả cầu khối lượng m treo ở đầu một sợi dây chiều dài l, đầu trên của dây cố định. Quả cầu nhận được vận tốc ban đầu vo theo phương ngang tại vị trí cân bằng. Bỏ qua sức cản của không khí.
a/ Tính vận tốc và lực căng của dây tại vị trí dây treo hợp với phương thẳng đứng góc α.
b/ Biết vo2 = 3gl. Tìm độ cao cực đại ho mà quả cầu đạt tới (tính từ vị trí cân bằng) trong chuyển đọng tròn. Độ cao Ho mà quả cầu đạt tới trong suốt quá trình chuyển động là bao nhiêu.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10

Bài 7. vật nặng m treo vào điểm cố định O bởi một dây dài l = 1m. Tại vị trí ban đầu Mo dây treo hợp với phương thẳng đứng góc αo = 60o, người ta truyền cho vật vận tốc vo = 5m/s theo phương vuông góc với dây, hướng xuống. véc tơ vo nằm trong mặt phẳng thẳng đứng.
a/ Xác định vị trsi M tại đó lực căng dây bằng không, tính vận tốc v của vật tại đó.
b/ Tìm phương trình quỹ đạo của giai đoạn chuyển động kế tiếp của vật cho đến khi dây căng trở lại. Chứng tỏ rằng quỹ đạo này đi qua điểm thấp nhất của quỹ đạo tròn. Suy ra thời gian vật vạch quỹ đạo nói trên.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10

Bài 8. Quả cầu nhỏ M có khối lượng 100g được treo tại A bởi một dây chiều dài l = 81cm. Tại O thấp hơn A khoảng l/2 có một chiếc đinh, AO có phương thẳng đứng. Kéo quả cầu đến vị trí dây AM nằm ngang rồi buông tay.
a/ Tính lực căng của dây ngay và trước sau khi vướng đinh
b/ HỎi ở điểm nào trên quỹ đạo, lực căng của dây treo bằng không? sau đó quả cầu chuyển động thế nào, lên tới độ cao lớn nhất bao nhiêu.

Bài 9. Quả cầu treo ở đầu một sợi dây. Truyền cho quả cầu ở vị trí cân bằng một vận tốc đầu theo phương ngang. Khi dây treo nghiêng góc α = 30o so với phương thẳng đứng, gia tốc quả cầu hướng nằm ngang. Tìm góc nghiêng cực đại của dây.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10

Bài 10. Hai vật A có m1 = 1,5kg; B có m2 = 0,45kg buộc vào các sợi dây treo trên một thanh đòn nhẹ, chiều dài hai nhanh tay đòn L1 = 0,6m; L2 = 1m. Vật A đặt trên sàn. Cần đưa dây treo B nghiêng góc α so với phương thẳng đứng nhỏ nhất bao nhiêu để sau khi buông tay vật A có thể nhấc khỏi bàn.
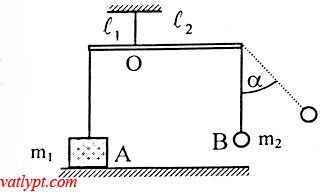
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
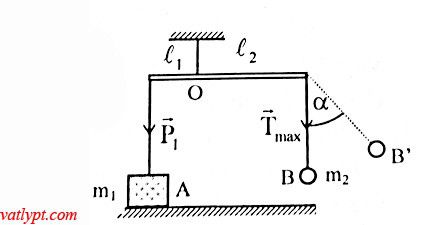
Tương tự bài 16 ta có
Tmax = m2g(3-2cosα)
Để A nhấc khỏi bàn thì momen của Tmax phải lớn hơn hoặc bằng momen của P1 cùng đối với trục quay nằm ngang đi qua điểm treo O của thanh đòn.
Tmax.L2 ≥ P1.L1 => m2g(3 – 2cosα)L2 ≥ m1gL1
=> cosα ≤ 0,5 => α ≥ 60o => αmin = 60o
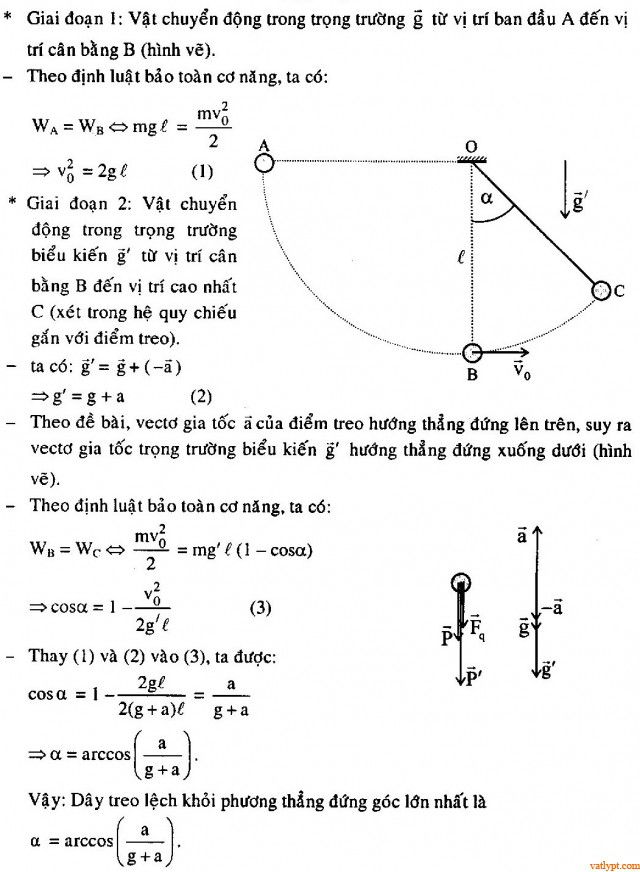
Bài 11. Quả cầu nhỏ treo ở đầu một dây nhẹ. Kéo quả cầu khỏi phương thẳng đứng để dây treo nghiêng góc 90o rồi buông tay. Tại thời điểm quả cầu qua vị trí cân bằng, điểm treo của nó chuyển động từ dưới lên với gia tốc a. Hỏi dây sẽ lệch khỏi phương thẳng đứng góc lớn nhất bao nhiêu.
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10
Bài 12. Quả cầu treo ở đầu dây có thể chuyển động tròn trong mặt phẳng thẳng đứng. Kéo quả cầu cho dây treo lệch góc α rồi buông tay. Khi quả cầu qua vị trí cân bằng B thì điểm treo rơi tự do. Tính α để khi quả cầu đến C, vận tốc quả cầu đối với mặt đất bằng 0.
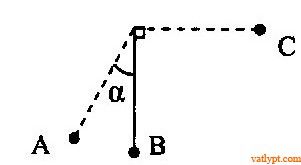
Hướng dẫn giải Bài tập Bảo toàn cơ năng con lắc đơn, vật lí 10

Bài 13. Hòn đá m = 0,5kg buộc vào sợi dây dài L =0,5m quay trong mặt phẳng thẳng đứng. Biết lực căng của dây ở điểm thấp nhất của quĩ đạo là T = 45N. Biết tại vị trí vận tốc hòn đá có phương thẳng đứng hướng lên thì dây đứt. Hỏi hòn đá sẽ lên đến độ cao bao nhiêu khi dây đứt (tính từ nơi dây bắt đầu đứt)
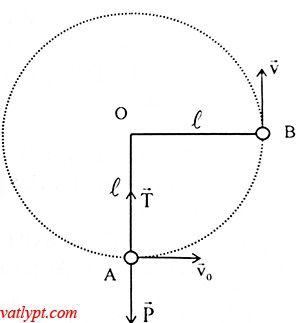
T – mgcosα = ma$_{ht}$ = mvo2/L => T = mgcosα + mvo2/L
=> v2 = (T-mg).L/m
Giả sử tại B dây đứt, gọi v là vận tốc của hòn đá lúc đứt dây
áp dụng định luật bảo toàn cơ năng
0,5mvo2 = mgL + 0,5mv2 => v2 = vo2 – 2gL
=> độ cao cực đại mà vật lên được H = v2/2g = 1,5m
Bài 14. Dây nhẹ không dãn chiều dài L = 50cm treo vật nặng nhỏ. Ban đầu vật nặng đứng yên ở vị trí cân bằng. Hỏi phải truyền cho vật nặng vận tốc tối thiểu bao nhiêu theo phương ngang để nó có thể chuyển động tròn trong mặt phẳng thẳng đứng.
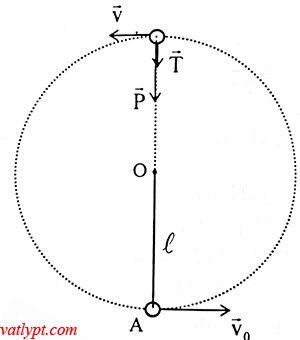
Gọi A là vị trí cân bằng. B là vị trí cao nhất của vật trong quá trình chuyển động. Chọn gốc thế năng tại A.
áp dụng định luật bảo toàn cơ năng
W$_{A}$ = W$_{B}$ => 0,5mvo2 = mg2L + 0,5mv2 => v2 = vo2 – 4gL (1)
Theo định luật II Newton
tại B: T + mg = ma$_{ht}$ = mv2/L
để vật có thể chuyển động tròn trong mặt phẳng thẳng đứng thì dây treo phải căng không trùng khi vật đi qua vị trí cao nhất B
=> T ≥ 0 => v2 ≥ gL (2)
từ (1) và (2) => vo ≥ \[\sqrt{5gL}\] = 5m/s
Bài 15. Quả cầu khối lượng m treo ở đầu sợi dây, chuyển động tròn trong mặt phẳng thẳng đứng trong một thang máy. Thang máy đi xuống nhanh dần đều với gia tốc 2g. Ở vị trí thấp nhất của quả cầu trong thang máy, lực căng dây bằng 0. Tính lực căng dây khi quả cầu ở vị trí cao nhất của quỹ đạo.

Đáp án tắc quá e k hiểu