Bài tập chuyển động ném xiên thuộc chủ đề vật lí lớp 10 Lực và chuyển động
Phương pháp giải bài tập ném xiên
Sử dụng công thức của chuyển động ném xiên hướng lên
- Thời gian vật đạt độ cao cực đại: $t_1 =\dfrac{v_o\sin\alpha}{g}$
- Tầm cao: \[H=\dfrac{v_{o}^{2}sin^{2}\alpha }{2g}\] + h
- Thời gian vật từ độ cao cực đại → đất: \[t_2 = \sqrt{\dfrac{2(H+ h)}{g}}\]
- Thời gian vật chạm đất kể từ lúc ném: $t = t_1 + t_2$
- Tầm xa: \[L=v_o\cos\alpha(t_1 + t_2)\] = $\dfrac{v_o^2\sin 2\alpha}{2g} + v_o\cos\alpha\sqrt{\dfrac{2(H+ h)}{g}}$
Coi chuyển động ném xiên hướng lên bao gồm 2 chuyển động:
- chuyển động ném xiên đi lên đến độ cao cực đại
- Từ độ cao cực đại đến khi vật chạm đất là chuyển động ném ngang
Bài tập ném xiên, bài tập chuyển động ném xiên
Bài 1. ném một vật từ điểm cách mật đất 25m với vận tốc ném là 15m/s theo phương hợp với phương ngang một góc 30o. Tình khoảng cách từ lúc ném vật đến lúc vật chạm đất và vận tốc khi vật chạm đất.
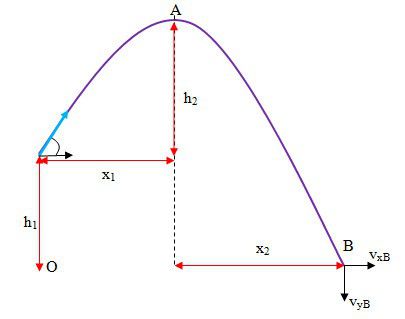
vo=15m/s; h1=25m; α=30o
Thời gian và vận tốc của vật khi đạt đến độ cao cực đại
t1=\[\dfrac{v_{o}\sin\alpha }{g}\]
=> x1=vocos30o.t1
Độ cao cực đại so với vị trí ném:
h2=\[\dfrac{v_{o}^{2}\sin^{2}\alpha }{2g}\]
Vận tốc tại đỉnh A: $v_{A}$=vo.cos30o
Thời gian vật từ vị trí A rơi đến khi chạm đất
t2=\[\sqrt{\dfrac{2(h_{1}+h_{2})}{g}}\]
=> x2=vocos30o.t2
=> khoảng cách từ vị trí ném đến vị trí vật chạm đất: x1 + x2
Vận tốc của vật khi chạm đất tại điểm B
$v_{B}$=\[\sqrt{v_{xB}^{2}+v_{yB}^{2}}\]
Trong đó: $v_{xB}$=vocos30o; $v_{yB}$=g.t2
Bài 2. Một vật ném xiên góc 45° từ mặt đất rơi cách đó 30m. Tính vận tốc khi ném, lấy g=10m/s2
Hướng dẫn giải bài tập ném xiên
Phân tích bài toán
α=45o ; L=30m; g=10m/s2
Giải
\[L=\dfrac{v_{o}^{2}sin2\alpha }{g}\]=30 => vo=10√3(m/s)
Bài 3. Từ A( độ cao AC = H = 3,6m) người ta thả một vật rơi tự do, cùng lúc đó từ B cách C đoạn BC = L = H người ta ném một vận khác với vận tốc ban đầu vo hợp với phương ngang góc α. Tính α và vo để hai vật gặp được nhau khi chúng đang chuyển động.
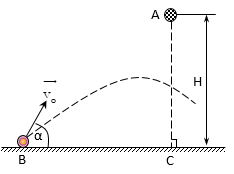
Hướng dẫn giải bài tập ném xiên
Chọn gốc tọa độ tại C, hệ trục tọa độ Oxy như hình vẽ
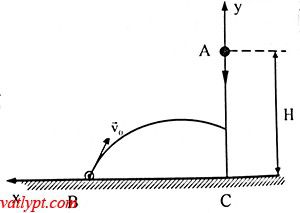
Phương trình vật thả rơi (vật I): x1 = 0; y1 = H – 0,5gt2
Phương trình vật II:
x2 = L – (vocosα)t = H – (vocosα)t
y2 = (vosinα)t – 0,5gt2
Để hai vật gặp nhau x1 = x2 và y1 = y2 =>
(vocosα)t = H
(vosinα)t = H
=> tanα = 1 => α = 45o => vo = \[\sqrt{\dfrac{2Hg}{\sin 2\alpha}}\] = 6m/s
Bài 4. Người ta đặt một súng cối dưới một căn hầm có độ sâu h. Hỏi phải đặt súng cách vách hầm một khoảng L bằng bao nhiêu so với phương ngang để tầm xa x của đạn trên mặt đất là lớn nhất. Tính tầm xa này biết vận tốc đạn khi rời súng là vo.
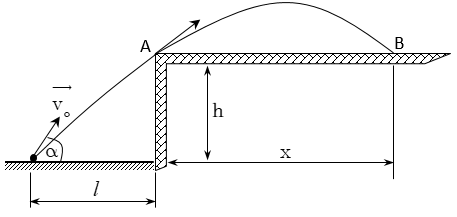
Hướng dẫn giải bài tập ném xiên

Bài 5. Một quả cầu được ném lên, xiên góc α với phương ngang vận tốc đầu 20m/s. Tìm độ cao, tầm xa, độ lớn và hướng vận tốc cuối của quả cầu khi góc α bằng
a/ 30o
b/ 45o
c/ 60o
Hướng dẫn giải bài tập ném xiên

Bài 6. Từ đỉnh dốc nghiêng góc β so với phương ngang, một vật được phóng đi với vận tốc vo hợp với phương ngang góc α. Hãy tính tầm xa của vật trên dốc.
Hướng dẫn giải bài tập ném xiên

Bài 7.Một bờ hồ nước có vách dựng đứng ở độ cao h so với mặt nước. Một nugời đứng trên bờ ném xiên một hòn đá với vận tốc đầu có độ lớn vo. Bỏ qua lực cản của không khí.
Tính góc tạo bởi \[\vec{v_o}\] và phương ngang để hòn đá rơi xuống mặt hồ xa bờ nhất
Hướng dẫn giải bài tập ném xiên

Bài 8.Một vật được buông rơi tự do xuống mặt phẳng nghiêng góc α so với phương ngang. Vật đụng mặt phẳng nghiêng và nẩy lên. Giả sử va chạm là tuyệt đối đàn hồi. Vật đụng mặt phẳng nghiêng liên tiếp ở các điểm 0, 1, 2 … Tìm tỉ lệ của khoảng cách giữa hai điểm đụng liên tiếp.
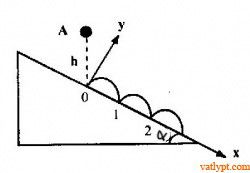
Hướng dẫn giải bài tập ném xiên

Bài 9. ném lên với vận tốc ban đầu \[5\left( m\text{/}s \right)\] theo phương hợp với mặt phẳng nằm ngang một góc \[\alpha ={{30}^{0}}\]. Lấy \[g=10\left( m\text{/}{{s}^{2}} \right)\].
a/ Viết phương trình chuyển động, phương tình đạo của hòn đá ?
b/ Sau bao lâu kể từ lúc ném, hòn đá sẽ chạm đất ?
c/ Khoảng cách từ chân tháp đến điểm rơi của vật ?
d/ Vận tốc của vật khi vừa chạm đất ?
ĐS: \[a\text{/ }\left\{ \begin{align}
& x=2,5\sqrt{3}t \\
& y=25+2,5t-5{{t}^{2}} \\
\end{align} \right..\text{ }b\text{/ }t=2,5\left( s \right).\text{ }c\text{/ }L=10,8\left( m \right).\text{ }d\text{/ }{{v}_{c}}=23\left( m\text{/}s \right)\].
Bài 10. Một vật được ném xiên từ mặt đất với vận tốc đầu \[{{v}_{o}}=50\left( m\text{/}s \right)\]. Khi lên đến đỉnh cao nhất, vận tốc của vật là \[v=40\left( m\text{/}s \right)\]. Lấy \[g=10\left( m\text{/}{{s}^{2}} \right)\].
a/ Tính góc nghiêng khi ném ?
b/ Viết phương trình quỹ đạo và vẽ quỹ đạo chuyển động của vật ?
c/ Tính tầm bay xa, tầm bay cao của vật ?
ĐS: \[a\text{/ }\alpha =36,{{87}^{0}}.\text{ }b\text{/ }y=-\dfrac{{{x}^{2}}}{320}+0,75x.\text{ }c\text{/ }L=240\left( m \right);\text{ }{{h}_{m\text{ax}}}=45\left( m \right)\].
Bài 11. Một vật được ném lên với vận tốc ban đầu \[2,67\left( m\text{/}s \right)\] chếch \[{{30}^{0}}\] so với phương ngang. Lấy \[g=9,8\left( m\text{/}{{s}^{2}} \right)\]. Xác định chuyển động của vật sau khi bị ném và thành lập phương trình quỹ đạo của vật ?
ĐS: \[x=2,31t;\text{ }y=1,335t-4,9{{t}^{2}}\].
Bài 12. Một vật được ném lên từ mặt đất theo phương xiên góc tại điểm cao nhất của quỹ đạo vật có vận tốc bằng một nửa vận tốc ban đầu và độ cao \[{{h}_{\max }}=15\left( m \right)\]. Lấy \[g=10\left( m\text{/}{{s}^{2}} \right)\].
a/ Tính ở độ lớn vận tốc ban đầu.Viết phương trình quỹ đạo của vật ?
b/ Tính tầm ném xa ?
c/ Ở độ cao nào vận tốc của vật hợp với phương ngang một góc \[{{30}^{0}}\]. Tính độ lớn vận tốc lúc ấy ?
ĐS: \[v=20\left( m\text{/}s \right)\].
Bài 13. Em bé ngồi dưới sàn nhà ném 1 viên bi lên bàn cao \[h=1\left( m \right)\] với vận tốc \[{{v}_{o}}=2\sqrt{10}\left( m\text{/}s \right)\]. Để viên bi có thể rơi xuống mặt bàn ở B xa mép bàn A nhất thì véctơ vận tốc \[\overrightarrow{{{v}_{o}}}\] phải nghiêng với phương ngang 1 góc bằng bao nhiêu ? Lấy \[g=10\left( m\text{/}{{s}^{2}} \right)\]. Tính AB và khoảng cách từ chổ ném O đến chân bàn H ?
ĐS: \[\alpha ={{60}^{0}};\text{ }AB=1\left( m \right);\text{ }OH=0,732\left( m \right)\].
Bài 14. Từ A (độ cao \[AC=H=3,6m\]), người ta thả một vật rơi tự do. Cùng lúc đó, từ B cách C đoạn \[BC=\mathrm{l}=H\] như hình vẽ, người ta ném một vật khác với vận tốc ban đầu \[\overrightarrow{{{v}_{o}}}\] hợp với góc α với phương ngang về phía vật thứ nhất. Tính α và vo để hai vật có thể gặp được nhau khi chúng đang chuyển động ?
ĐS: \[{{v}_{o}}\ge 6\left( m\text{/}s \right);\text{ }\alpha ={{45}^{0}}\].
Bài 15. Từ đỉnh dốc nghiêng góc β so với phương ngang, một vật được phóng đi với vận tốc vo hợp với phương ngang một góc α. Hãy tính tầm xa của vật trên mặt dốc ?
ĐS: \[s=\dfrac{2v_{o}^{2}\cos \alpha .\sin \left( \alpha +\beta \right)}{g{{\cos }^{2}}\beta }\].
Bài 16. Một người đặt một súng cối dưới một căn hầm có độ sâu h. Hỏi phải đặt súng cách vách hầm một khoảng l bằng bao nhiêu so với phương ngang để tầm xa x của đạn trên mặt đất là lớn nhất ? Tính tầm xa này ? Biết vận tốc ban đầu của đạn khi rời súng là vo.
ĐS: \[\left\{ \begin{align}
& \mathrm{l}=\dfrac{v_{o}^{2}}{g}\left[ \sqrt{\dfrac{1}{4}-{{\left( \dfrac{gh}{v_{o}^{2}} \right)}^{2}}}-\left( \dfrac{1}{2}-\dfrac{gh}{v_{o}^{2}} \right) \right] \\
& AB=2\left( \dfrac{1}{2}-\dfrac{gh}{v_{o}^{2}} \right) \\
\end{align} \right.\].
Bài 17. Một bờ hồ nước có vách dựng đứng ở độ cao h so với mặt nước. Một người đứng trên bờ ném xiên một hòn đá với vận tốc đầu vo. Bỏ qua lực cản không khí. Tính góc hợp bởi véctơ vận tốc ban đầu \[\overrightarrow{{{v}_{o}}}\] và phương ngang để hòn đá rơi xuống mặt hồ xa bờ nhất ?
ĐS: \[\tan \alpha =\dfrac{{{v}_{o}}}{\sqrt{v_{o}^{2}+2gh}}\].
Bài 18. Từ A cách mặt đất một khoảng \[AB=45\left( m \right)\], người ta ném một vật với vận tốc [{{v}_{01}}=30\left( m\text{/}s \right)\] theo phương ngang. Cho \[g=10\left( m\text{/}{{s}^{2}} \right)\].
a/ Trong hệ qui chiếu nào vật chuyển động với gia tốc g ? Trong hệ qui chiếu nào vật chuyển động thẳng đều ? Viết phương trình chuyển động của vật trong mỗi hệ qui chiếu ?
b/ Cùng lúc ném vật từ A, tại B trên mặt đất (với \[BH=AB\]) người ta ném lên một vật khác với vận tốc \[\overrightarrow{{{v}_{02}}}\]. Định \[\overrightarrow{{{v}_{02}}}\] để hai vật gặp nhau được ?
ĐS: \[a\text{/ }\left\{ \begin{align}
& y=5{{t}^{2}} \\
& x=30t \\
\end{align} \right..\text{ }b\text{/ }{{v}_{02}}=\dfrac{{{v}_{01}}}{\sin \alpha -\cos \alpha }\] với góc \[\alpha \] hợp với phương ngang một góc thỏa mãn đẳng thức: \[{{45}^{0}}<\alpha <{{135}^{0}}\].
Bài 19. Một vật được ném lên với vận tốc ban đầu \[60\left( m\text{/}s \right)\] chếch \[{{30}^{0}}\] so với phương ngang. Sau \[4\left( s \right)\] vật rơi vào một sườn của một ngọn đồi. Lấy \[g=9,8\left( m\text{/}{{s}^{2}} \right)\].
a/ Vận tốc của vật tại điểm cao nhất ?
b/ Khoảng cách từ điểm phóng đến điểm chạm vào sườn đồi ?
ĐS: \[a\text{/ }v=52\left( m\text{/}s \right).\text{ }b\text{/ }211\left( m \right)\].
Ném một quả bóng có khối lợng 0.1 kg ở độ cao 10m với vận tốc ban đầu 20m/s, góc ném nghiêng với ph-ơng nằm ngang một góc bằng 300 về phía một bức t-ờng cao thẳng đứng, cách vị trí ném 15m. Biết rằng lực ma sát tỷ lệ với vận tốc, hệ số tỷ lệ bằng 0.05kg/s và gia tốc tr-ờng hấp dẫn bằng 9.8 m/s,
quả bóng va chạm đàn hồi với bức t ờng a/ Xác định thời điểm và độ cao của quả bóng khi chạm t-ờng.
b/ Tính và vẽ đồ thị x, y, vx, vy theo thời gian và quĩ đạo của quả bóng từ khi ném tới khi chạm đất.
Xác định thời điểm quả bóng chạm đất và nó cách t ờng một khoảng bằng bao nhiêu
giúp em bài này với ạ
bài này chắc dùng giải tích
trả lời như trả lời