Bài tập đồ thị chuyển động thẳng biến đổi đều
Đồ thi vận tốc thời gian (v-t) của chuyển động thẳng biến đổi đều
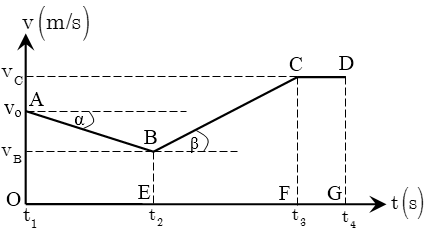
Đồ thị \[tOv\] là đường thẳng xiên góc, bắt đầu từ vị trí \[\left( t=0,v={{v}_{o}} \right)\], hướng lên nếu \[a>0\], hướng xuống nếu \[a<0\]. Đồ thị \[v-t\] của hai vật có cùng vận tốc thì song song.
Đoạn AB:
- Chuyển động chậm dần đều.
- Vận tốc ban đầu: \[{{v}_{o}}\].
- Gia tốc: \[a=\dfrac{{{v}_{B}}-{{v}_{o}}}{{{t}_{2}}-{{t}_{1}}}\]. Nếu cho góc
\[\alpha \] thì \[a=\tan \alpha \]. - Quãng đường đi là diện tích hình phẳng
giới hạn bởi hình thang ABEO.
Đoạn BC:
- Chuyển động nhanh dần đều.
- Vận tốc ban đầu là \[{{v}_{B}}\] và gia tốc \[a=\dfrac{{{v}_{C}}-{{v}_{B}}}{{{t}_{3}}-{{t}_{2}}}\], nếu cho góc \[\beta \] thì \[a=\tan \beta \].
- Quãng đường đi là diện tích hình phẳng giới hạn bởi hình thang BCFE.
Đoạn CD:
- Chuyển động thẳng đều (vận tốc \[{{v}_{C}}={{v}_{D}}\] không thay đổi theo thời gian).
- Gia tốc \[a=0\] và quãng đường đi là diện tích hình phẳng giới hạn bởi hình chữ nhật CDGF.
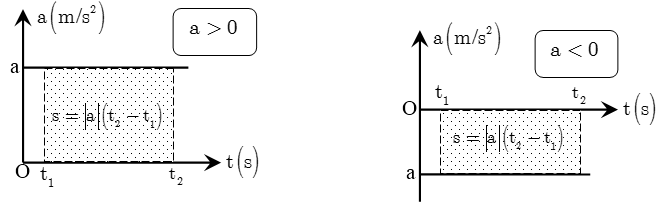
Đồ thị gia tốc – thời gian của chuyển động thẳng biến đổi đều
là đường thẳng song song với trục Ot:
- Nằm trên nếu .
- Nằm dưới nếu .
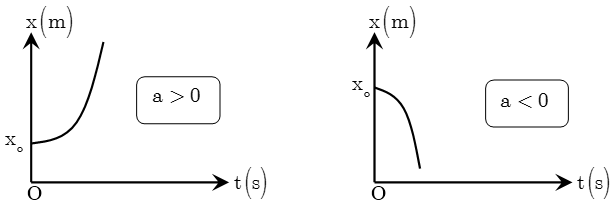
Đồ thị tọa độ – thời gian của chuyển động thẳng biến đổi đều
Đồ thị tọa độ – thời gian: là đường cong (nhánh hyperbol) bắt đầu từ vị trí , bề lõm hướng lên nếu , bề lõm hướng xuống nếu .
Bài 1. Một chuyển động thẳng có đồ thị vận tốc – thời gian như hình vẽ.
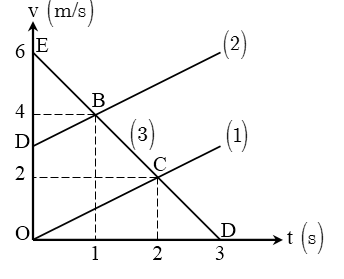
a/ Mô tả tính chất chuyển động của vật này.
b/ Các đoạn thẳng OC, OD và OE trên các trục tọa độ tương ứng với những đại lượng nào ?
c/ Sau bao nhiêu giây thì vật thứ ba sẽ dừng lại ?
d/ Dựa vào các đồ thị \[\left( 1 \right),\left( 2 \right),\left( 3 \right)\]. Hãy xác định gia tốc chuyển động của các vật ?
ĐS: a/ \[t=3\left( s \right)\]. b/ \[{{a}_{\left( 1 \right)}}={{a}_{\left( 2 \right)}}=1\left( m\text{/}{{s}^{2}} \right),\text{ }{{a}_{\left( 3 \right)}}=-2\left( m\text{/}{{s}^{2}} \right)\].
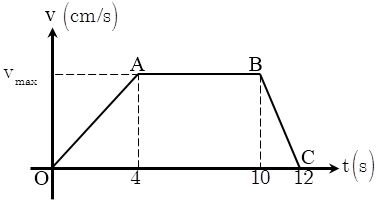
Bài 2. Một chất điểm chuyển động thẳng có đồ thị vận tốc – thời gian như hình vẽ bên.
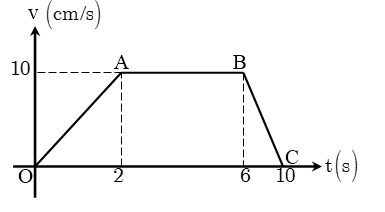
a/ Tính gia tốc của chất điểm trong mỗi giai đoạn ?
b/ Lập phương trình chuyển động của chất điểm trong mỗi giai đoạn ?
c/ Tính quãng đường chất điểm chuyển động trong \[10\left( s \right)\] ?
d/ Vẽ đồ thị tọa độ – gia tốc theo thời gian ?
ĐS: \[{{a}_{OA}}=5\left( cm\text{/}s \right),{{a}_{AB}}=0,{{a}_{BC}}=-2,5\left( cm\text{/}{{s}^{2}} \right)\].
Bài 3. Một chất điểm chuyển động thẳng có đồ thị vận tốc – thời gian như hình vẽ bên.
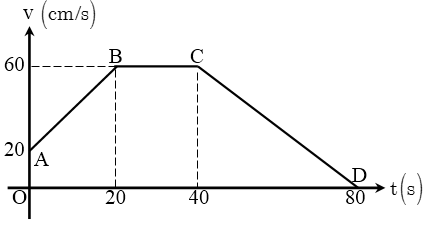
Xác định loại chuyển động ứng với mỗi đoạn của đồ thị và xác định gia tốc tương ứng. Lập phương trình vận tốc ứng với từng đoạn trên đồ thị. Tính quãng đường vật đã đi ?
ĐS: \[{{a}_{AB}}=2\left( m\text{/}{{s}^{2}} \right)\], \[{{s}_{AB}}=800\left( m \right)\].
\[{{a}_{BC}}=0\], \[{{s}_{BC}}=1200\left( m \right)\].
\[{{a}_{CD}}=-1,5\left( m\text{/}{{s}^{2}} \right)\], \[{{s}_{CD}}=1200\left( m \right)\] và \[\sum{s=3200\left( m \right)}\].
Bài 4. Đồ thị vận tốc thời gian của một vật chuyển động như hình vẽ bên.
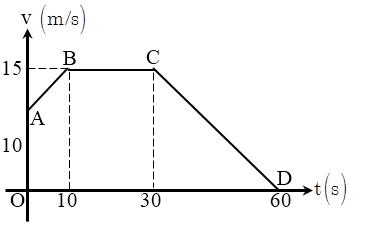
a/ Nêu tính chất chuyển động của mỗi giai đoạn ?
b/ Lập phương trình vận tốc cho mỗi giai đoạn ?
ĐS: \[\left\{ \begin{matrix}
& {{v}_{AB}}=10+0,5t\text{ }\left( 0\le t\le 10 \right) \\
& {{v}_{BC}}=15 \\
& {{v}_{CD}}=15-0,5\left( t-30 \right);\text{ }\left( 30\le t\le 60 \right) \\
\end{matrix} \right.\]
Bài 5. Cho đồ thị vận tốc – thời gian của hai ô tô như hình vẽ.
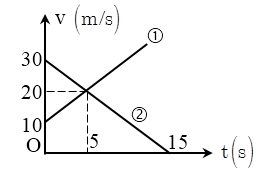
a/ Xác định loại chuyển động ? Lập công thức tính vận tốc ?
b/ Ý nghĩa giao điểm của hai đồ thị ?
ĐS: \[\left\{ \begin{matrix}
& {{v}_{1}}=10+2t\text{ }\left( t\ge 0 \right) \\
& {{v}_{2}}=30-2t \\
\end{matrix} \right.\]
Bài 6. Một người ngồi trên xe trượt tuyết xuống một dốc dài \[40\left( m \right)\] mất \[10\left( s \right)\] khi đến chân dốc, sau đó đà trượt đưa xe đi thêm \[20\left( m \right)\] nữa trên đường nằm ngang mới dừng lại. Xem các chuyển động là biến đổi đều.
a/ Tính vận tốc tại chân dốc ? Biết vận tốc lúc bắt đầu trượt bằng 0.
b/ Gia tốc trên mỗi đoạn đường ?
c/ Thời gian chuyển động ?
d/ Vẽ đồ thị vận tốc – gia tốc theo thời gian.
ĐS: \[8\left( m\text{/}s \right);\text{ }0,8\left( cm\text{/}{{s}^{2}} \right);\text{ }1,6\left( cm\text{/}{{s}^{2}} \right);\text{ }15\left( s \right)\].
Bài 7. Đồ thị vận tốc thời gian của một vật chuyển động như hình vẽ bên.

a/ Lập các phương trình vận tốc ?
b/ Tính quãng đường vật đã đi được ?
ĐS: \[\left\{ \begin{matrix}
& {{v}_{AB}}=30 \\
& {{v}_{BC}}=30-15\left( t-2 \right);\text{ }\left( 2\le t\le 4 \right) \\
& {{v}_{CD}}=10\left( t-4 \right);\text{ }\left( 4\le t\le 8 \right) \\
\end{matrix} \right.\]
Bài 8. Một chất điểm chuyển động thẳng có đồ thị vận tốc – thời gian như hình vẽ. Trong suốt quá trình chuyển động, vận tốc trung bình là \[9\left( m\text{/}s \right)\].
a/ Tính gia tốc chuyển động của chất điểm trong mỗi giai đoạn ?
b/ Lập phương trình chuyển động của chất điểm trong mỗi giai đoạn ?
c/ Vẽ đồ thị tọa độ – gia tốc theo thời gian ?
ĐS: \[{{a}_{OA}}=3\left( m\text{/}{{s}^{2}} \right);\text{ }{{a}_{AB}}=0;\text{ }{{a}_{BC}}=-6\left( m\text{/}{{s}^{2}} \right)\].