Bài tập chuyển động rơi tự do: bài toán thả rơi
Phương pháp giải bài tập rơi tự do bài toán thả rơi (vo = 0)
Các công thức cơ bản của thả rơi tự do
- quãng đường rơi: s = 0,5gt2
- thời gian rơi: $t=\sqrt{\dfrac{2\text{s}}{g}}$
- vận tốc rơi: v = gt
- quãng đường rơi trong giây thứ n: ${{s}_{n}}=a(n-0,5)$
- quãng đường rơi được trong n giây cuối: $\Delta {{S}_{n}}=na(t-0,5n)$
Bài tập chuyển động rơi tự do: bài toán thả rơi tự do
Bài 1. Thả rơi tự do một vật khối lượng 2kg từ độ cao 180m xuống mặt đất, Lấy g = 10m/s2.
a/ Tính quãng đường vật rơi được trong giây cuối cùng.
b/ Tính vận tốc của vật trước khi vật chạm đất 2 giây.
Phân tích bài toán
h = 180m, g = 10m/2; vo = 0
gọi t là thời gian từ lúc thả rơi đến lúc vật chạm đất
Giải
a/ h = 0,5gt2 = > t = 6s
s6 = 0,5.g.62 – 0,5.g.52 = 55m
b/ v = g(6-2) = 40m/s
Bài 2. Quãng đường rơi được trong giây cuối cùng của vật rơi tự do là 63,7m. Tính độ cao thả vật, thời gian và vận tốc của vật khi chạm đất, lấy g = 9,8 m/s2.
vo = 0; $s_{t}$ = 63,7m; g = 9,8m/s2
Gọi t là thời gian vật rơi đến khi chạm đất = > quãng đường vật rơi được trong giây cuối = quãng đường vật rơi chạm đất “trừ đi” quãng đường vật rơi trước đó 1 giây (t-1)
$s_{t}$ = 0,5gt2 – 0,5g(t-1)2 = 63,7 = > t = 7s
h = 0,5gt2 = 240,1m
v = gt = 68,6m
Bài 3. Thả một vật rơi tự do ở độ cao 80m so với mặt đất. Lấy g = 10m/s2, một giây sau cũng tại nơi đó một vật khác được ném thẳng đứng hướng xuống với vận tốc vo. Hai vật chạm đất cùng lúc xác định vo .
Gọi t là thời gian vật 1 thả rơi tự do chạm đất = > \[t = \sqrt{\dfrac{2h}{g}}\] = 4(s)
thời gian vật 2 chạm đất là t2 = t-1 = 3s
= > h = vot2 + 0,5gt22
= > vo = 35/3 (m/s)
Bài 4. Ở độ cao 300m so với mặt đất trên một kinh khí cầu người ta thả một vật rơi tự do. Tính thời gian vật chạm đất trong các trường hợp sau: (lấy g = 9,8m/s2)
a) Khí cầu đang đứng yên.
b) Khí cầu chuyển động thẳng đều đi lên với vận tốc 4,9m/s
c) Khí cầu chuyển động thẳng đều đi xuống với vận tốc 4,9m/s
Phân tích bài toán
Chọn gốc tọa độ tại vị trí thả vật, chiều dương hướng xuống dưới
a/ vo = 0; g = 9,8m/s2; h = 300m
b/ vo = -4,9m/s; g = 9,8m/s2; h = 300m
c/ vo = 4,9m/s; g = 9,8m/s2; h = 300m
Giải
a/ h = 0,5gt2 = > t = 7,8s
b/ h = vot + 0,5gt2 = > t = 8,3 (s)
c/ h = vot + 0,5gt2 = > t = 7,3 (s)
Bài 5. Thả cách nhau 0,1 giây hai vật rơi tự do ở độ cao h so với mặt đất. Biết khi vật đầu chạm đất thì vật thứ hai cách mặt đất 0,95m. Tính độ cao thả vật lấy g = 10m/s2.
Phân tích bài toán
Gọi t là thời gian vật rơi chạm đất
v$_{o1}$ = v$_{o2}$ = 0; h – $s_{t-0,1}$ = 0,95; g = 10m/s2
rơi tự do các vật rơi như nhau nên bài toán có thể được giải theo hướng: thả một vật rơi tự do ở độ cao h, quãng đường vật rơi được trong 0,1 giây cuối là 0,95m. Tính độ cao thả vật.
Giải
h – $s_{t-0,1}$ = 0,95 = > 0,5gt2 – 0,5g(t-0,1)2 = 0,95 = > t = 1 (s)
= > h = 0,5gt2 = 5m
Bài 6. Thả rơi tự do một vật từ độ cao 180m so với mặt đất, đồng thời ném một vật từ mặt đất lên với vận tốc 80m/s, lấy g = 10m/s2.
a/ Tìm độ cao so với mặt đất và thời gian hai vật gặp nhau.
b/ Sau bao lâu độ lớn vận tốc của hai vật bằng nhau.
gốc tọa độ, thời gian tại vị trí thả, chiều dương hướng xuống
vật rơi y1 = $\dfrac{1}{2}$gt2
vật ném: y2 = 180 – 80t + ½gt2
a/ gặp nhau = > y1 = y2 = > t = 2,25s
= > độ cao gặp nhau: h = 180 – ½g × 2,252 = 154,6875m
b/ v1 = gt = v2 = 80 – gt = > t = 4s
Bài 7. Để xác định chiều sâu của một cái hang người ta thả hòn đá từ miệng hang sau đó tính thời gian nghe thấy tiếng hòn đá chạm đáy vọng lại. Coi chuyển động của hòn đá là chuyển động rơi tự do, thời gian từ lúc thả rơi đến khi nghe thấy tiếng hòn đá chạm vào đáy hang là 4s, lấy g = 9,8m/s2, tốc độ truyền âm trong không khí là 330m/s. Tính chiều sâu của hang.
vo = 0; thời gian vật rơi chạm đáy: [tex]t_{1} = \sqrt{\dfrac{2h}{g}}[/tex]
thời gian âm thanh truyền từ đáy về miệng hang: [tex]t_{2} = \dfrac{h}{330}[/tex] (chuyển động của âm thanh là chuyển động thẳng đều với vận tốc v = s/t)
t1 + t2 = 4s = > $\sqrt{\dfrac{2h}{g}}$ + $\dfrac{h}{330}$ = 4 = > h = 70m
Bài 8: Một giọt nước rơi từ mái nhà xuống sau những khoảng thời gian bằng nhau. Khi giọt nước thứ nhất rơi chạm đất thì giọt thứ năm bắt đầu rơi. Tìm khoảng cách giữa các giọt kế tiếp nhau biết rằng mái nhà cao 45m, lấy g = 10m/s2
Thời gian giọt 1 rơi chạm đất: h = 0,5gt2 = > t = 3(s)
Khoảng thời gian giữa 5 giọt liên tiếp: t1 = t2 = t3 = t4 = t/4 = 0,75(s)
Khoảng cách từ giọt thứ 5 đến giọt thứ 4: $s_{54}$ = 0,5gt12 = 2,8125 (m)
Khoảng cách từ giọt thứ 4 đến giọt thứ 3:
$s_{43}$ = 0,5g(t1 + t2)2 – $s_{54}$ = 8,4375(m)
Khoảng cách từ giọt thứ 3 đến giọt thứ 2: $s_{32}$ = 0,5g(t1 + t2+ t3)2 – $s_{43}$ – $s_{54}$ = 14.0625(m)
Khoảng cách từ giọt thứ 2 đến giọt thứ 1: $s_{21}$ = h – $s_{32}$ – $s_{43}$ – $s_{54 }$ = 19,6875 (m)
Bài 9: từ mặt đất ném hai vật lên theo phương thẳng đứng lên trên với cùng một vận tốc ban đầu 10m/s và cách nhau một khoảng thời gian t = 0,5s. Hỏi sau bao lâu kể từ lúc ném vật thứ nhất và ở độ cao nào thì hai vật sẽ gặp nhau. Bỏ qua sức cản của không khí và lấy g = 10m/s2
gọi t1 là thời gian vật 1 đạt đến độ cao cực đại (v1 = 0) kể từ khi ném
v1 = vo – gt1 = 0 = > t1 = 1 (s)
độ cao cực đại mà vật 1 đạt được so với vị trí ném
s1 = 0,5gt12 = 5m
Chọn gốc thời gian là lúc vật 1 đạt độ cao cực đại, gốc tọa độ tại vị trí ném, chiều dương hướng lên.
Phương trình chuyển động của 2 vật
x1 = 5 – 0,5gt2 (1)
lưu ý vật 2 ném sau vật 1 là 0,5 giây = > khi vật 1 đạt độ cao cực đại thì vật 2 cách vị trí ném một khoảng là:
x$_{o2}$ = 0,5gt22 = 0,5.10.(0,5)2 = 1,25m
vận tốc của vật 2 sau 0,5giây là: v2 = gt2 = 5(m/s) = >
x2 = 1,25 + 5t – 0,5gt2 (2)
hai vật gặp nhau = > x1 = x2 = > t = 0,85(s)
= > sau 1,85 giây kể từ khi ném thì hai vật gặp nhau cách vị trí ném một khoảng là
x = 5 – 0,5g(0,85)2 = 1,3875 (m)
Bài 10: Một vật rơi tự do đi được 10m cuối cùng của quãng đường trong khoảng thời gian 0,25s. Lấy g = 10m/s2.
a/ Tính vận tốc của vật khi chạm đất.
b/ Tính độ cao vật bắt đầu rơi
c/ Nếu từ độ cao này người ta ném thẳng đứng một vật khác thì phải ném với vận tốc bằng bao nhiêu và phải theo hướng nào để vật rơi xuống tới mặt đất chậm hơn (và nhanh hơn ) vật rơi tự do khoảng thời gian 1s.
a/ Gọi độ cao vật rơi tự do là h, t là thời gian vật chạm đất
Vận tốc của vật khi chạm đất: v = gt
vận tốc của vật trước đó 0,25s: vo = g(t-0,25)
ta có v2 – vo2 = 2gs = > t = \[\dfrac{33}{8}\] = 4,125 (s) = > v = g.t = 41,25 (m/s)
b/ h = 0,5gt2 = 85 (m)
c/ Để vật khác rơi chậm hơn thì ném lên, rơi nhanh hơn thì ném xuống
Trường hợp ném lên với vận tốc vo để vật rơi chậm hơn 1s
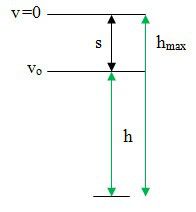
Thời gian vật lên đến độ cao cực đại
v = vo – gt’1 = 0 = > t’1 = vo/g.
v2 – vo2 = -2g.s = > s = vo2/2g
thời gian vật từ độ cao cực đại rơi xuống
hmax = 0,5gt’22 = > h + s = 0,5gt’22 = > t’2 = \[\sqrt{2.\dfrac{s+h}{g}}\]
vật chạm đất chậm hơn 1 giây = > t’1 + t’2 = t + 1 = 5,125
giải phương trình trên = > v$_{o }$ = 8,36 (m/s)
Trường hợp vật ném xuống với vận tốc vo để rơi nhanh hơn 1s
h = vo(t-1) + 0,5g(t-1)2 = > vo = 11,575 (m/s)
Bài 11: Thả một vật ở độ cao h so với mặt đất. Lấy g = 10m/s2. Tính độ cao thả vật và vận tốc của vật khi chạm đất nếu
a/ Trong giây cuối cùng vật rơi được 3/4h
b/ Trong 2 giây cuối cùng vật rơi được 3/4 quãng đường.
Gọi t là thời gian vật rơi chạm đất ta có h = 0,5gt$^{2 }$(1)
a/ Quãng đường vật đi được trong 1 giây cuối
s = 0,5g[t2 – (t-1)2] = \[\dfrac{3}{4}\]h (2)
từ (1) và (2) = > t = 2 = > h = 20m = > v = 20m/s
b/ Quãng đường vật đi được trong 2 giây cuối
s = 0,5g[t2 – (t-2)2] = \[\dfrac{3}{4}\]h (3)
từ (1) và (3) = > t = 4 = > h = 80m = > v = 40m/s
Bài 12: Một cây thước dài 1m, được thả rơi sao cho trong khi rơi thước luôn thẳng đứng. Phải thả từ độ cao nào để nó đi qua mép bàn trong 0,2 giây?
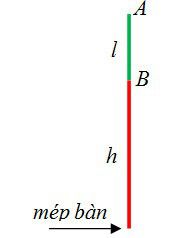
ℓ = 1m
Thời gian điểm B (đầu dưới của thước đi qua mép bàn): h = 0,5gt2 (1)
Thời gian điểm A (đầu trên của thước đi qua mép bàn): h + ℓ = 0,5g(t + 0,2)2 (2)
Từ (1) và (2) = > t = 0,4 (s) = > h = 0,8m
Bài 13: Chiều cao cửa sổ là 1,4m. Giọt mưa trước rời mái nhà rơi đến mép dưới cửa sổ thì giọt tiếp sau rơi tới mép trên cửa sổ, lúc này, vận tốc 2 giọt mưa hơn nhau 1m/s
a/ Tìm khoảng thời gian giữa hai lần liên tiếp giọt mưa rời mái nhà.
b/ Tìm chiều cao của mái nhà
s = 1,4m; v1 vận tốc mép trên cửa sổ, v2: vận tốc mép dưới cửa sổ
v2 = v1 + gt = > v1 + 1 = v1 + gt = > t = 0,1s
v22 – v12 = 2g.s = > (v1 + 1)2 – v12 = 2gs = > v1 = 13,5 (m/s) = > v2 = 14,5 (m/s)
Chiều cao của mái nhà so với mép dưới cửa sổ (nơi giọt nước bắt đầu rơi vo = 0)
v22 – vo2 = 2gh = > h = 10,5m
Bài 14: Trong 0.5s cuối cùng trước khi chạm đất, vật rơi tự do rơi được quãng đường gấp đôi quãng đường rơi được trong 0.5s ngay trước đó. Tìm độ cao từ vị trí được thả rơi.
Gọi t là thời gian vật rơi chạm đất = > h = 0,5gt2
Quãng đường rơi trong 0,5 giây cuối: s1 = 0,5g[t2 – (t-0,5)2]
Quãng đường rơi trong 0,5 giây trước đó: s2 = 0,5g[(t-0,5)2 – (t-0,5-0,5)2]
s1 = 2s2 = > t = 1,25s = > h = 0,5gt2 = 7,8125m
Bài 15. Cho hai vật rơi tự do từ hai độ cao khác nhau xuống đất. Thời gian rơi của vật (1) gấp đôi thời gian rơi của vật (2). So sánh
– quãng đường rơi của hai vật
– vận tốc rơi của hai vật.

Bài 16. Một vật rơi tự do tại nơi có gia tốc g = 10m/s2. Trong 2 giây cuối vật rơi được 180m. Tính thời gian rơi và độ cao thả rơi.

Bài 17. Một vật rơi tự do tại nơi có g = 10m/s2. Thời gian rơi là 10s. Tính
a/ Thời gian vật rơi 1m đầu tiên
b/ Thời gian vật rơi 1m cuối cùng.

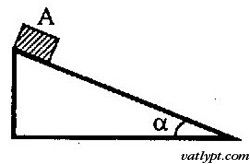
Bài 18. Vật A đặt trên mặt phẳng nghiêng của một cái nêm như hình vẽ. Hỏi phải truyền cho nêm gia tốc bao hiêu theo phương ngang để vật A rơi tự do xuống dưới theo phương thẳng đứng.

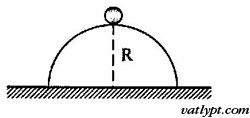
Bài 19. Một bán cầu có bán kính R trượt đều theo đường thẳng nằm ngang. Một quả cầu nhỏ cách mặt phẳng ngang một đoạn bằng R. Ngay khi đỉnh bán cầu đi qua quả cầu nhỏ thì nó được buông rơi. Tìm vận tốc nhỏ nhất của bán cầu để nó không cản trở sự rơi tự do của quả cầu nhỏ. Cho R = 40cm.

Bài 20. Một thang máy chuyển động lên cao với gia tốc 2m/s2. Lúc thang máy có vận tốc 2,4m/s thì từ trần thang máy có một vật rơi xuống. Trần thang máy cách sàn là 2,47m. Hãy tính trong hệ quy chiếu gắn với mặt đất
a/ Thời gian rơi
b/ độ dịch chuyển của vật
c/ quãng đường vật đã đi được.

Bài 21. Một vật rơi tự do từ độ cao h. Cùng lúc đó một vật được ném thẳng xuống từ độ cao H > h với vận tốc đầu vo. Hai vật tới đất cùng lúc. Tìm vo

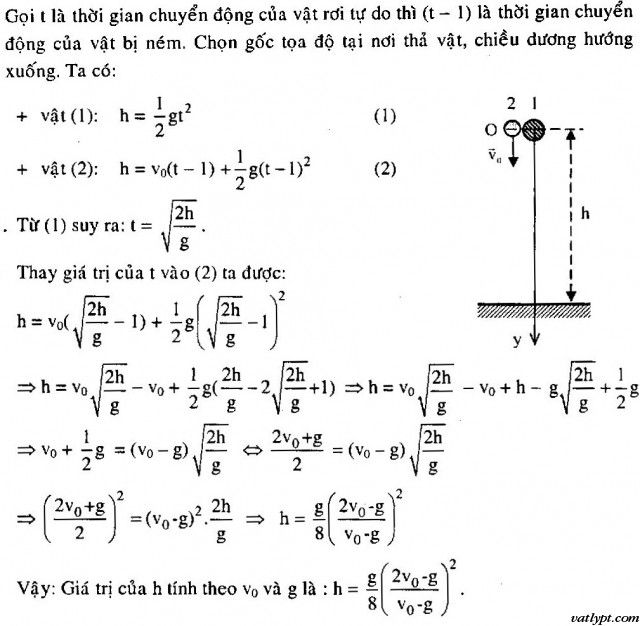
Bài 22. Một vật thả rơi tự do ở độ cao h. Một giây sau, cũng tại nơi đó một vật khác được ném thẳng đứng hướng xuống với vận tốc vo. Hai vật chạm đất cùng lúc tính h theo vo và g.
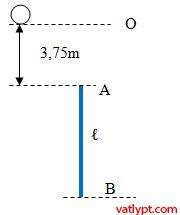
Bài 23. Từ trên cao,người ta thả rơi một hòn bi ,sau đó to giây người ta thả một chiếc thước dài rơi thẳng đứng. Ban đầu điểm cao nhất của thước thấp hơn độ cao ban đầu của bi là 3,75 m.Khi hòn bi đuổi kịp thước thì chênh lệch vận tốc hai vật là 5 m/s.Sau khi đuổi kịp thước 0,2 giây thì hòn bi vượt qua được thước. Tính to,chiều dài thước,quãng đường bi đi được cho đến lúc đuổi kịp thước và độ cao ban đầu tối thiểu của hòn bi để nó vượt qua được thước.(Cho g = 10 m/s^2)
Chọn gốc thời gian là lúc bắt đầu thả bi, gốc tọa độ tại O chiều + hướng xuống
bi: x1 = $\dfrac{1}{2}$gt2
điểm A: x2 = 3,75 + $\dfrac{1}{2}$g(t – to)2
điểm B: x3 = 3,75 + ℓ + $\dfrac{1}{2}$g(t – to)2
bi đuổi kịp = > x1 = x2 = > $\dfrac{1}{2}$gt12 = 3,75 + $\dfrac{1}{2}$g(t1 – to)2(1)
v1 = v2 + 5 = > gt1 = g(t1– to) + 5 (2)
từ (1) và (2) = > t1; t$_{o }$ = > quãng đường s = $\dfrac{1}{2}$gt12
bắt đầu vượt qua = > x1 = x3 = > $\dfrac{1}{2}$g(t1 + 0,2) = x2 = 3,75 + ℓ + $\dfrac{1}{2}$g(t1+ 0,2 – to)$^{2 }$ = > ℓ
độ cao tối thiểu h = 3,75 + ℓ + $\dfrac{1}{2}$g(t1 + 0,2 – to)2
Bài 24. Thả rơi một vật từ độ cao 74,8m. Tính quãng đường vật rơi trong giây đầu tiên và giây cuối cùng. Thời gian vật đi hết 20m đầu tiên và 20m cuối cùng.
h = 74,8m.
thời gian rơi chạm đất: h = $\dfrac{1}{2}$gt2 = > t
quãng đường rơi trong giây đầu: $s_{1đ}$ = $\dfrac{1}{2}$g × 12
quãng đường rơi trong giây cuối: $s_{1c}$ = ½g{t2 – (t-1)2}
thời gian đi 20m đầu: $s_{đ}$ = $\dfrac{1}{2}$gt12 = 20 = > t1
thời gian đi (74,8 – 20) m: s = $\dfrac{1}{2}$gt22 = 54,8 = > t2
thời gian đi 20m cuối: t$_{c}$ = t – t2
Bài 25. Từ độ cao h của 1 đỉnh tháp so với mặt đất, người ta thả rơi 1 vật. Một giây sau, ở tầng tháp thấp hơn 40m, người ta thả rơi 1 vật khác. Cả 2 vật chạm đất cùng lúc. Lấy g = 10m/s2. Tìm
a. Thời gian rơi của 1 vật
b. Độ cao của tháp
c. Vận tốc của mỗi vật khi chạm đất
a/ Chọn gốc tọa độ, thời gian tại vị trí vật 1 rơi, chiều dương hướng xuống = > phương trình chuyển động:
vật 1: y1 = $\dfrac{1}{2}$gt2
vật 2: y2 = 40 + $\dfrac{1}{2}$g(t – 1)2
hai vật chạm đất cùng lúc tương đương với gặp nhau tại mặt đất
= > y1 = y2 = > $\dfrac{1}{2}$gt$^{2 }$ = 40 + $\dfrac{1}{2}$g(t – 1)$^{2 }$ = > t = 4,5 (s)
b/ h = $\dfrac{1}{2}$gt2 = 101,25m
c/ v = gt = 45m/s
bai ao that day