Lý thuyết tổng hợp lực, phân tích lực, các phương pháp tính độ lớn của lực nằm trong chủ đề Vật lí lớp 10 Lực và chuyển động
Lực là gì?
Lực là đại lượng vectơ đặc trưng cho sự tác dụng của vật này lên vật khác, biểu hiện của nó là gây ra gia tốc hoặc làm vật biến dạng.
Biểu diễn lực: bằng một đại lượng véc tơ có
- Điểm đặt: nằm tại vật chịu tác dụng của lực
- Phương, chiều: trùng với véc tơ biểu diễn lực
- Độ lớn lực: tỉ lệ với độ dài của véc tơ biểu diễn lực
Video bài giảng lực, tổng hợp lực, phân tích lực
Tổng hợp lực theo phương pháp hình bình hành
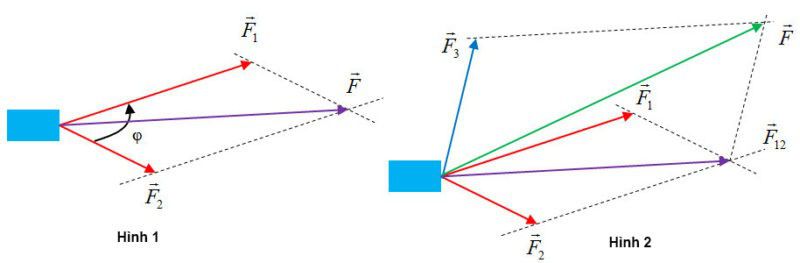
Phân tích lực theo quy tắc hình bình hành trên 2 phương cho trước
Nguyên tắc phân tích lực: trong các bài toán vật lí cơ bản, chúng ta phân tích lực dựa trên phương cho sẵn, thông thường chúng ta phân tích lực bình thường thành 2 lực thành phần (thành phần thứ nhất có phương vuông góc với phương chọn sẵn, thành phần thứ hai có phương song song với phương chọn sẵn)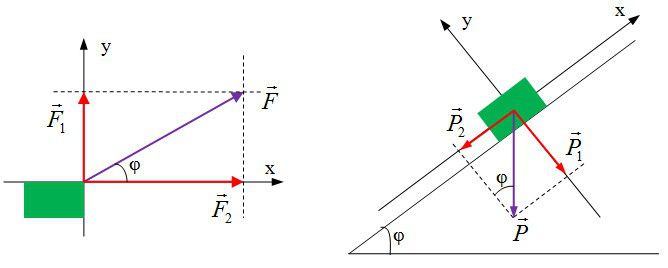
Tính độ lớn lực tổng hợp theo quy tắc hình bình hành
\[\vec{F}=\vec{F_{1}}+\vec{F_{2}}\]→ \[F=\sqrt{F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}cos\varphi }\]
=> | F1 – F2 | ≤ F ≤ F1 + F2
các trường hợp đặc biệt:
\[\vec{F_{1}}\uparrow \uparrow \vec{F_{2}}\] => F=F1 + F2
\[\vec{F_{1}}\uparrow \downarrow \vec{F_{2}}\] => F=| F1 – F2 |
\[\vec{F_{1}}\perp \vec{F_{2}}\] => \[F=\sqrt{F_{1}^{2}+F_{2}^{2}}\]
\[\vec{F_{1}}=\vec{F_{2}}\] => \[F=2F_{1}\cos\dfrac{\varphi}{2}\]
Tính độ lớn của lực, hợp lực thông qua các tính chất hình học
Nguyên tắc vận dụng để tính độ lớn của lực thông qua hình học: Coi độ lớn của lực bằng độ dài hình học mà nó được biểu diễn thông qua phân việc phân tích lực.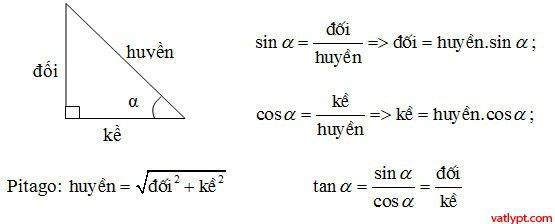
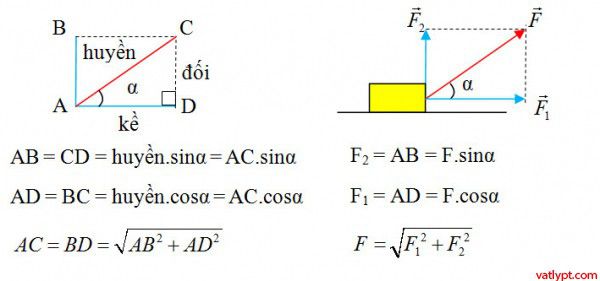

Tính độ lớn của lực, hợp lực thông qua các định lý của tam giác thường
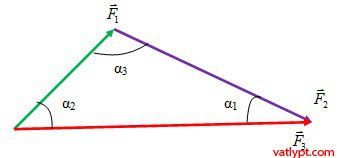
\[F_{3}^{2}=F_{1}^{2}+F_{2}^{2}-2F_{1}F_{2}cos\alpha _{3}\]
\[F_{1}^{2}=F_{3}^{2}+F_{2}^{2}-2F_{3}F_{2}cos\alpha _{1}\]
\[F_{2}^{2}=F_{1}^{2}+F_{3}^{2}-2F_{1}F_{3}cos\alpha _{2}\]
Sử dụng định lý hàm sin trong tam giác:
\[\dfrac{F_1}{\sin{\alpha_1}}=\dfrac{F_2}{\sin{\alpha_2}}=\dfrac{F_3}{\sin{\alpha_3}}\]
Ví dụ về Bài tập Tổng hợp lực, phân tích lực, độ lớn của lực vật lí 10
Bài tập 1. Tính hợp lực của ba lực đồng qui trong một mặt phẳng. Biết góc hợp giữa 1 lực với hai lực còn lại đều là các góc 60$^{o }$và độ lớn của ba lực đều bằng 20N.
Hướng dẫn giải bài tập tính độ lớn lực
$F_{13}=2F_{1}\cos{\dfrac{120}{2}}$ = 20N
F1 = F3 → F13 có phương trùng với đường phân giác của góc hợp bởi $\vec{F_1}$; $\vec{F_3}$
→ $\vec{F_{13}}$ ↑↑ $\vec{F_2}$ → F = F2 + F13 = 40N