Hàm số đơn điệu trên miền K
Phương pháp: Sử dụng các kiến thức sau đây:
1. Cho hàm số y = f(x) có đạo hàm trên K.
- Nếu $f'(x) \ge 0,\,\,\forall x \in K$ thì f(x) đồng biến trên K.
- Nếu $f'(x) \le 0,\,\,\forall x \in K$ thì f(x) nghịch biến trên K.
2. Cho tam thức bậc hai f(x) = ax2 + bx + c có biệt thức $\Delta = {b^2} – 4ac$. Ta có:
- $f(x) \ge 0,\,\,\forall x \in R\, \Leftrightarrow \left\{ \begin{array}{l} a > 0\\ \Delta \le 0 \end{array} \right.$
- $f(x) \le 0,\,\,\forall x \in R\, \Leftrightarrow \left\{ \begin{array}{l} a < 0\\ \Delta \le 0 \end{array} \right.$
3. Xét bài toán: “Tìm m để hàm số y = f(x,m) đồng biến trên K”. Ta thực hiện theo các bước sau:
- Bước 1. Tính đạo hàm f’(x,m).
- Bước 2. Lý luận: Hàm số đồng biến trên K$ \Leftrightarrow f'(x,m) \ge 0,\,\,\forall x \in K \Leftrightarrow m \ge g(x),\forall x \in K\,\,\left( {m \le g(x)} \right)$
- Bước 3. Lập bảng biến thiên của hàm số g(x) trên K. Từ đó suy ra giá trị cần tìm của tham số m.
Sử dụng định lý về điều kiện cần
- Nếu hàm số f (x) đơn điệu tăng trên R thì $f’\left( x \right) \geqslant 0,\forall x \in R$.
- Nếu hàm số f (x) đơn điệu giảm trên R thì $f’\left( x \right) \leqslant 0,\forall x \in R$
Ví dụ minh họa
Ví dụ 1 : Tìm m để các hàm số sau luôn nghịch biến trên mỗi khoảng xác định $y = \dfrac{{mx + 3 – 2m}}{{x + m}}$
- Hàm số đã cho xác định trên khoảng (—∞; —m) ∪ (—m; +∞)
- Ta có $y’ = \dfrac{{{m^2} + 2m – 3}}{{{{\left( {x + m} \right)}^2}}},x \ne – m$
Bảng xét dấu y’

Dựa vào bảng xét dấu ta thấy: Nếu —3 < m < 1 thì y’ < 0 hàm số nghịch biến trên mỗi khoảng (—∞; —m), (—m; + ∞) .
Ví dụ 2 : Tìm m để các hàm số sau luôn nghịch biến trên mỗi khoảng xác định $y = \dfrac{{ – 2{x^2} + \left( {m + 2} \right)x – 3m + 1}}{{x – 1}} = – 2x + m + \dfrac{{1 – 2m}}{{x – 1}}$
- Hàm số đã cho xác định trên khoảng (—∞; 1) ∪ (1; +∞) .
- Ta có: $y’ = – 2 + \dfrac{{2m – 1}}{{{{\left( {x – 1} \right)}^2}}},x \ne 1$
+ $m \leqslant \dfrac{1}{2} \Rightarrow y’ < 0,x \ne 1,$ do đó hàm số nghịch biến trên mỗi khoảng (- ∞; 1), (1; + ∞) .
+ m > 0,5 khi đó phương trình y’ = 0 có hai nghiệm x1 < 1 < x2 => hàm số đồng biến trên mỗi khoảng (x1; 1) và (1; x2), trường hợp này không thỏa .
Vậy $m \leqslant \dfrac{1}{2}$ thỏa mãn yêu cầu của bài toán
Ví dụ 3 : Tìm m để các hàm số sau luôn nghịch biến trên R: $y = – \dfrac{1}{3}{x^3} + 2{x^2} + \left( {2m + 1} \right) – 3m + 2$
- Hàm số đã cho xác định trên R.
- Ta có : $y’ = – {x^2} + 4x + 2m + 1$ và ∆’ = 2m + 5
Bảng xét dấu ∆’
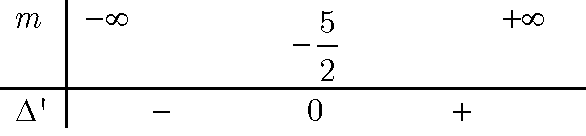
Do đó hàm số nghịch biến trên R.
+ m <- 2,5 thì y’ < 0, ∀x ∈ R. Do đó hàm số nghịch biến trên R.
+ m > – 2,5 thì y’ = 0 có hai nghiệm x1, x2 (x1 < x2). Hàm số đồng biến trên khoảng (x1;x2). Trường hợp này không thỏa mãn.
Ví dụ 4: Tìm m để các hàm số sau luôn nghịch biến trên R: $y = \dfrac{{\left( {m + 2} \right)}}{3}{x^3} – \left( {m – 2} \right){x^2} + \left( {m – 8} \right)x + {m^2} – 1$
- Hàm số đã cho xác định trên R.
- Ta có y’ = (m + 2)x$^2$ – 2(m + 2)x + m – 8 .
+ m = -2, khi đó y’ = -10 ≤ 0, ∀x ∈ R => hàm số luôn nghịch biến trên R.
+ m ≠ -2 tam thức y’ = (m + 2)x$^2$ – 2(m + 2)x + m – 8 có ∆’ = 10(m + 2)
Bảng xét dấu ∆’
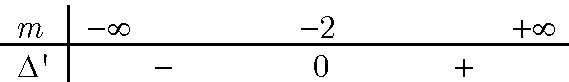
+ m < -2 thì y’ < 0 với mọi x ∈ R. Do đó hàm số nghịch biến trên R.
+ m > -2 thì y’ = 0 có hai nghiệm x1,x2 (x1 < x2). Hàm số đồng biến trên khoảng (x1; x2) . Trường hợp này không thỏa mãn .
Vậy m ≤ -2 là những giá trị cần tìm.
Ví dụ 5 : Tìm a để các hàm số sau luôn đồng biến trên R: $y = \dfrac{{{x^3}}}{3} + a{x^2} + 4x + 3$
- Hàm số đã cho xác định trên R.
- Ta có y ‘ = x$^2$ + 2ax + 4 và có ∆’ = a$^2$ – 4
Bảng xét dấu ∆’
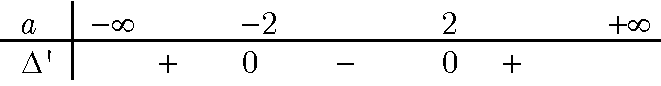
+ Nếu -2 < a < 2 thì y’ > 0 với mọi x ∈ R. Hàm số y đồng biến trên R.
+ Nếu a = 2 thì y’ = (x + 2)$^2$ , ta có : y’ = 0 <=>x = -2, y’ > 0, x ≠ -2 . Hàm số y đồng biến trên mỗi nửa khoảng (- ∞; -2] và [-2; + ∞)nên hàm số y đồng biến trên R.
+ Tương tự nếu a = -2 . Hàm số y đồng biến trên R.
+ Nếu a < -2 hoặc a > 2 thì y ‘ = 0 có hai nghiệm phân biệt x1, x2. Giả sử x1 < x2. Khi đó hàm số nghịch biến trên khoảng (x1; x2 ),đồng biến trên mỗi khoảng (- ∞;x1)và (x2; + ∞). Do đó a < -2 hoặc a > 2 không thoả mãn yêu cầu bài toán .
Vậy hàm số y đồng biến trên R khi và chỉ khi —2 ≤ a ≤ 2 .
Ví dụ 6: Tìm a để các hàm số sau luôn đồng biến trên R: $y = \dfrac{1}{3}\left( {{a^2} – 1} \right){x^3} + \left( {a + 1} \right){x^2} + 3x + 5$
Hàm số đã cho xác định trên R.
Ta có : y ‘ = (a$^2$ -1)x$^2$ + 2(a + 1)x + 3 và có ∆’ = 2( – a$^2$ + a + 2)
Hàm số y đồng biến trên R khi và chỉ khi <=> y’ ≥ 0, ∀x ∈ R (1)
+ Xét a$^2$ -1 = 0 <=> a = ±1
- a = 1 => y’ = 4x + 3=> y’ ≥ 0 <=> x ≥ – 4/3 => a = 1 không thoả yêu cầu bài toán.
- a = 1 => y’ = 3> 0 ∀ x ∈ R => a = – 1 thoả yêu cầu bài toán.
+ Xét a$^2$ — 1 ≠ ±1
* Bảng xét dấu ∆’
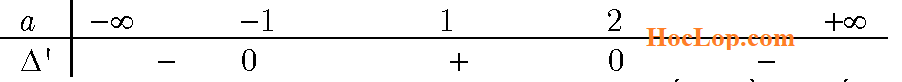
- Nếu a < —1 V a > 2 thì y’ > 0 với mọi x ∈ R. Hàm số y đồng biến trên R.
- Nếu a = 2 thì y’ = 3 (x + 1)$^2$ , ta có : y’ = 0 <=> x = —1, y’ > 0, x ≠ —1. Hàm số y đồng biến trên mỗi nửa khoảng (- ∞; —1] và [ – 1; + ∞) nên hàm số y đồng biến trên R.
- Nếu —1 < a < 2, a ≠ 1 thì y’ = 0 có hai nghiệm phân biệt x1, x2. Giả sử x1 < x2. Khi đó hàm số nghịch biến trên khoảng (x1; x2 ) ,đồng biến trên mỗi khoảng (- ∞; x1) và (x2; + ∞) . Do đó —1 < a < 2, a ≠ 1 không thoả mãn yêu cầu bài toán .
Do đó hàm số y đồng biến trên R khi và chỉ khi a < —1 V a ≥ 2 . Vậy với 1 ≤ a ≤ 2 thì hàm số y đồng biến trên R.
Chú ý:
Phương pháp:
- Hàm số y = f (x, m) tăng trên R <=> y’ > 0 ∀ x ∈ R <=>min y’ ≥ 0.
- Hàm số y = f (x, m) giảm trên R<=>y’ < 0 ∀x ∈ R max y’ ≤ 0.
1) Nếu y’ = ax$^2$ +bx + c thì
$y’ \geqslant 0\,\forall x \in R \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} a = b = 0 \hfill \\ c \geqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} a > 0 \hfill \\ \Delta \leqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$
$y’ \leqslant 0\,\forall x \in R \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} a = b = 0 \hfill \\ c \leqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} a < 0 \hfill \\ \Delta \leqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$
2) Hàm đồng biến trên R thì nó phải xác định trên R