Hai mặt phẳng song song, trắc nghiệm toán 11
Câu 1: Một mặt phẳng cắt hai mặt đối diện của hình hộp theo hai giao tuyến là $a$ và $b$. Hãy Chọn câu đúng:
[A]. $a$ và $b$ song song.
[B]. $a$ và $b$ chéo nhau.
[C]. $a$ và $b$ trùng nhau
[D]. $a$ và $b$ cắt nhau.
Chọn [A].
Câu 2: Chọn câu đúng :
[A]. Hai đường thẳng a và b không cùng nằm trong mặt phẳng (P) nên chúng chéo nhau
[B]. Hai đường thẳng không song song thì chéo nhau
[C]. Hai đường thẳng phân biệt lần lượt nằm trên hai mặt phẳng khác nhau thì chéo nhau
[D]. Hai đường thẳng không song song và lần lượt nằm trên hai mặt phẳng song song thì chéo nhau
Chọn [D].
A sai vì còn trường hợp song song.
B sai vì còn trường hợp cắt nhau.
C sai vì còn trường hợp song song.
Câu 3: Chọn câu đúng :
[A]. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song
[B]. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau
[C]. Hai mặt phẳng không cắt nhau thì song song
[D]. Hai mặt phẳng không song song thì trùng nhau
Chọn [A]. Theo hệ quả 2 sgk trang 66.
Câu 4: Hãy Chọn câu sai :
[A]. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia
[B]. Nếu mặt phẳng $\left( P \right)$ chứa hai đường thẳng cùng song song với mặt phẳng $\left( Q \right)$ thì $\left( P \right)$ và $\left( Q \right)$ song song với nhau
[C]. Nếu hai mặt phẳng $\left( P \right)$ và (Q) song song nhau thì mặt phẳng $\left( R \right)$ đã cắt $\left( P \right)$ đều phải cắt $\left( Q \right)$ và các giao tuyến của chúng song song nhau
[D]. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng còn lại
Chọn [B].
Theo định lý 1 trang 64 sgk: Nếu mặt phẳng $\left( P \right)$ chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng $\left( Q \right)$ thì $\left( P \right)$ và $\left( Q \right)$ song song với nhau
Câu 5: Cho một đường thẳng song song với mặt phẳng . Có bao nhiêu mặt phẳng chứa và song song với ?
[A]. 0
[B]. 1
[C]. 2
[D]. vô số
Chọn [B].
Có duy nhất một mặt phẳng chứa và song song với .
Câu 6: Hãy chọn câu đúng :
[A]. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mọi đường thẳng nằm trên mặt phẳng kia
[B]. Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau
[C]. Hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau
[D]. Hai mặt phẳng phân biệt không song song thì cắt nhau
Chọn [D].
Câu 7: Cho một điểm nằm ngoài mp. Qua vẽ được bao nhiêu đường thẳng song song với ?
[A]. 1
[B]. 2
[C]. 3
[D]. vô số
Chọn [D].
Qua vẽ được vô số đường thẳng song song với .
Câu 8: Giả thiết nào sau đây là điều kiện đủ để kết luận đường thẳng song song với mp?
[A]. a//b và a // (α).
[B]. a// b và \[b\subset (\alpha)\].
[C]. $a//(\beta) và $(\beta) // (\alpha)$.
[D]. \[a \cap \alpha = \varnothing \]
Chọn [D].
Theo định nghĩa SGK Hình học 11.
Câu 9: Cho đường thẳng \[a\] nằm trên mp \[\left( \alpha \right)\] và đường thẳng \[b\] nằm trên mp \[\left( \beta \right)\]. Biết \[\left( \alpha \right)\text{//}\left( \beta \right)\].
Tìm câu sai:
[A]. \[a\text{//}\left( \beta \right)\].
[B]. \[b\text{//}\left( \alpha \right)\].
[C]. \[a\text{//}b\].
[D]. Nếu có một mp \[\left( \gamma \right)\] chứa \[a\] và \[b\] thì \[a\text{//}b\].
Chọn [C].
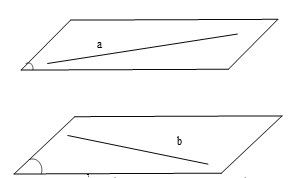
vì còn có khả năng $a,\,\,b\,$
chéo nhau như hình vẽ sau.
Câu 10: Cho đường thẳng $a$ nằm trong mặt phẳng $\left( \alpha \right)$ và đường thẳng $b$ nằm trong mặt phẳng $\left( \beta \right)$. Mệnh đề nào sau đây SAI?
[A]. \[\left( \alpha \right)\text{//}(\beta )\Rightarrow a\text{//}b\].
[B]. \[\left( \alpha \right)\text{//}(\beta )\Rightarrow a\text{//}\left( \beta \right)\].
[C]. \[\left( \alpha \right)\text{//}(\beta )\Rightarrow b\text{//}\left( \alpha \right)\].
[D]. \[a\] và $b$ hoặc song song hoặc chéo nhau.
Chọn [A].
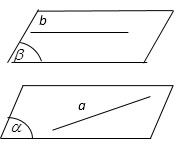
Nếu \[\left( \alpha \right)\text{//}\left( \beta \right)\] thì ngoài trường hợp \[a\text{//}b\] thì \[a\]và $b$ còn có thể chéo nhau.
Câu 11: Cho đường thẳng \[a\subset mp\left( P \right)\] và đường thẳng \[b\subset mp\left( Q \right).\] Mệnh đề nào sau đây đúng?
[A]. \[\left( P \right)//\left( Q \right)\Rightarrow a//b.\]
[B]. \[a//b\Rightarrow \left( P \right)//\left( Q \right).\]
[C]. \[\left( P \right)//\left( Q \right)\Rightarrow a//\left( Q \right)\text{ }v\grave{a}\text{ }b//\left( P \right).\]
[D]. $a$ và $b$ cắt nhau.
Chọn C
Nếu $\left( P \right)//\left( Q \right)$ thì mọi đường thẳng \[a\subset mp\left( P \right)\] đều song song với $mp\left( Q \right)$ và mọi đường thẳng \[b\subset mp\left( Q \right)\] đều song song với $mp\left( P \right).$
Câu 12: Hai đường thẳng $a$ và $b$ nằm trong $\left( \alpha \right)$. Hai đường thẳng ${a}’$ và ${b}’$ nằm trong mp$\left( \beta \right)$. Mệnh đề nào sau đây đúng?
[A]. Nếu \[a\,\text{//}\,{a}’\] và \[b\,\text{//}\,{b}’\] thì $\left( \alpha \right)\text{//}\left( \beta \right)$.
[B]. Nếu $\left( \alpha \right)\text{//}\left( \beta \right)$ thì \[a\,\text{//}\,{a}’\] và \[b\,\text{//}\,{b}’\].
[C]. Nếu \[a\,\text{//}\,b\] và \[{a}’\,\text{//}\,{b}’\] thì $\left( \alpha \right)\text{//}\left( \beta \right)$.
[D]. Nếu $a$ cắt $b$, $a$ cắt $b$và \[a\,\text{//}\,{a}’\] và \[b\,\text{//}\,{b}’\] thì $\left( \alpha \right)\text{//}\left( \beta \right)$.
Chọn D
Do \[a\,\text{//}\,{a}’\]nên $a\,\text{//}\left( \beta \right)$ và \[b\,\text{//}\,{b}’\]nên $b\,\text{//}\left( \beta \right)$.
Theo định lí 1 bài hai mặt phẳng song song, thì $\left( \alpha \right)\text{//}\left( \beta \right)$.
DẠNG 1: CHỨNG MINH HAI MẶT PHẲNG SONG SONG
Phương pháp 1
Cơ sở của phương pháp chứng minh hai mặt phẳng \[(\alpha )\] và \[(\beta )\] song song nhau là:
– Bước 1: Chứng minh mặt phẳng \[(\alpha )\] chứa hai đường thẳng \[a,b\] cắt nhau lần lượt song song với hai đường thẳng \[{a}’,{b}’\] cắt nhau trong mặt phẳng \[(\beta )\].
– Bước 2: Kết luận \[(\alpha )\parallel (\beta )\] theo điều kiện cần và đủ.
Phương pháp 2
– Bước 1: Tìm hai đường thẳng \[a,b\] cắt nhau trong mặt phẳng \[(\alpha )\].
– Bước 2: Lần lượt chứng minh \[a\parallel (\beta )\] và \[b\parallel (\beta )\]
– Bước 3: Kết luận \[(\alpha )\parallel (\beta )\].
Câu 13: Cho hình hộp $ABCD.{A}'{B}'{C}'{D}’$. Khẳng định nào sau đây SAI?
[A]. $A{B}'{C}’D$ và ${A}’BC{D}’$ là hai hình bình hành có chung một đường trung bình.
[B]. $B{D}’$ và ${B}'{C}’$ chéo nhau.
[C]. ${A}’C$ và \[D{D}’\] chéo nhau.
[D]. $D{C}’$ và $A{B}’$ chéo nhau.
Chọn [D].
$D{C}’$ và $A{B}’$ song song với nhau.
Câu 14: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}’\]. Mặt phẳng \[\left( A{B}'{D}’ \right)\] song song với mặt phẳng nào trong các mặt phẳng sau đây?
[A]. \[\left( BC{A}’ \right)\].
[B]. \[\left( B{C}’D \right)\].
[C]. \[\left( {A}'{C}’C \right)\].
[D]. \[\left( BD{A}’ \right)\].
Chọn [B].
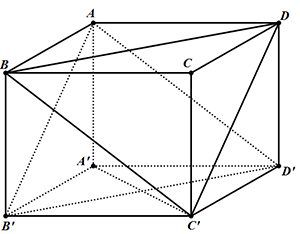
Do \[AD{C}'{B}’\] là hình bình hành nên \[A{B}’\text{//}D{C}’\], và \[AB{C}'{D}’\] là hình bình hành nên \[A{D}’\text{//}B{C}’\] nên \[\left( A{B}'{D}’ \right)\text{//}\left( B{C}’D \right)\].
Câu 15: Cho hình hộp \[ABCD.{A}'{B}'{C}'{D}’\]. Gọi \[M\] là trung điểm của \[AB\]. Mặt phẳng $\left( M{A}'{C}’ \right)$ cắt hình hộp \[ABCD.{A}'{B}'{C}'{D}’\] theo thiết diện là hình gì?
[A]. Hình tam giác.
[B]. Hình ngũ giác.
[C]. Hình lục giác.
[D]. Hình thang.
Chọn [D].
Trong mặt phẳng $\left( AB{B}'{A}’ \right)$, $AM$ cắt $B{B}’$ tại $I$
Do $MB\text{//}{A}'{B}’;\,\,MB=\dfrac{1}{2}{A}'{B}’$ nên $B$ là trung điểm ${B}’I$ và $M$ là trung điểm của $I{A}’$.
Gọi $N$ là giao điểm của $BC$ và ${C}’I$.
Do $BN\text{//}{B}’C$ và $B$ là trung điểm ${B}’I$ nên $N$ là trung điểm của ${C}’I$.
Suy ra: tam giác $I{A}'{C}’$ có $MN$ là đường trung bình.
Ta có mặt phẳng $\left( M{A}'{C}’ \right)$ cắt hình hộp \[ABCD.{A}'{B}'{C}'{D}’\] theo thiết diện là tứ giác ${A}’MN{C}’$ có $MN\text{//}{A}'{C}’$
Vậy thiết diện là hình thang ${A}’MN{C}’$.
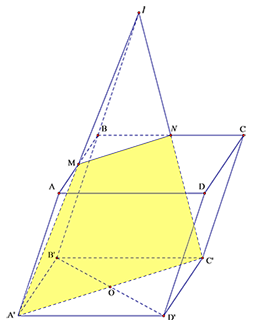
Cách khác:
Ta có :$\left\{ \begin{align}
& \left( ABCD \right)\text{//}\left( {A}'{B}'{C}'{D}’ \right) \\
& \left( {A}'{C}’M \right)\cap \left( {A}'{B}'{C}'{D}’ \right)={A}'{C}’ \\
& \left( {A}'{C}’M \right)\cap \left( ABCD \right)=Mx \\
\end{align} \right.$ $\Rightarrow Mx\text{//}{A}'{C}’$, $M$ là trung điểm của $AB$ nên $Mx$ cắt $BC$ tại trung điểm $N$.Thiết diện là tứ giác ${A}'{C}’NM$.
Câu 16: Cho hình bình hành \[ABCD\]. Vẽ các tia \[Ax,By,Cz,Dt\] song song, cùng hướng nhau và không nằm trong mp\[\left( ABCD \right)\]. Mp $\left( \alpha \right)$ cắt \[Ax,By,Cz,Dt\] lần lượt tại\[{A}’,{B}’,{C}’,{D}’\]. Khẳng định nào sau đây sai?
[A]. \[{A}'{B}'{C}'{D}’\] là hình bình hành.
[B]. mp\[\left( A{A}'{B}’B \right)\text{// }\left( D{D}'{C}’C \right)\].
[C]. \[A{A}’=C{C}’\] và \[B{B}’=D{D}’\].
[D]. \[O{O}’\text{// }A{A}’\].
($O$ là tâm hình bình hành \[ABCD\], \[{O}’\] là giao điểm của \[{A}'{C}’\] và\[{B}'{D}’\]).
Chọn [C].
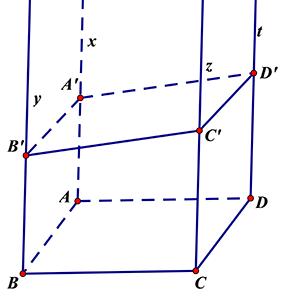
$\left. \begin{align}
& AB\,\,\text{//}\,\,DC \\
& A{A}’\,\,\text{//}D{D}’ \\
& AB,A{A}’\subset \left( AB{B}'{A}’ \right) \\
& DC,D{D}’\subset \left( D{D}'{C}’C \right) \\
\end{align} \right\}$$\Rightarrow \left( AB{B}'{A}’ \right)\,\,\text{//}\,\,\left( D{D}'{C}’C \right)$.
Câu B đúng.
Mặt khác
$\left. \begin{align}
& \left( \alpha \right)\cap \left( AB{B}'{A}’ \right)={A}'{B}’ \\
& \left( \alpha \right)\cap \left( DC{C}'{D}’ \right)={C}'{D}’ \\
& \left( AB{B}'{A}’ \right)\,\text{//}\,\left( DC{C}'{D}’ \right) \\
\end{align} \right\}$$\Rightarrow {A}'{B}’\,\,\text{//}\,\,{C}'{D}’$
$\left. \begin{align}
& \left( \alpha \right)\cap \left( AD{D}'{A}’ \right)={A}'{D}’ \\
& \left( \alpha \right)\cap \left( BC{C}'{B}’ \right)={C}'{B}’ \\
& \left( AB{B}'{A}’ \right)\,\text{//}\,\left( DC{C}'{D}’ \right) \\
\end{align} \right\}$$\Rightarrow {A}'{D}’\,\,\text{//}\,\,{C}'{B}’$
Do đó câu A đúng.
$O,{O}’$ lần lượt là trung điểm của $AC,{A}'{C}’$ nên $O{O}’$ là đường trung bình trong hình thang $A{A}'{C}’C$. Do đó \[O{O}’\text{// }A{A}’\]. Câu D đúng.
Câu 17: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}’\]. Người ta định nghĩa ‘Mặt chéo của hình hộp là mặt tạo bởi hai đường chéo của hình hộp đó’. Hỏi hình hộp \[ABCD.{A}'{B}'{C}'{D}’\] có mấy mặt chéo ?
[A]. $4$.
[B]. $6$.
[C]. $8$.
[D]. $10$.
Chọn [B].
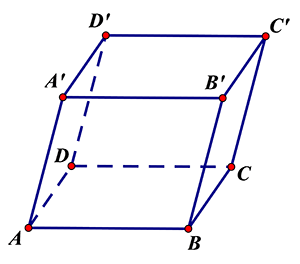
Các mặt chéo của hình hộp là $\left( AD{C}'{B}’ \right);\left( {A}'{D}’CB \right);\left( AB{C}'{D}’ \right)$
$\left( DC{B}'{A}’ \right);\left( AC{C}'{A}’ \right);\left( BD{D}'{B}’ \right)$
Câu 18: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}’\]. Mp\[(\alpha )\] qua \[AB\] cắt hình hộp theo thiết diện là hình gì?
[A]. Hình bình hành.
[B]. Hình thoi.
[C]. Hình vuông.
[D]. Hình chữ nhật.
Chọn [A].
Câu 19: Cho hình hộp \[ABCD.{A}'{B}'{C}'{D}’\]. Gọi $O$ và \[{O}’\] lần lượt là tâm của \[AB{B}'{A}’\] và\[DC{C}'{D}’\].Khẳng định nào sau đây sai ?
[A]. \[\overrightarrow{O{O}’}=\overrightarrow{AD}\].
[B]. $O{O}’\text{//}\left( AD{D}'{A}’ \right)$.
[C]. \[O{O}’\] và \[B{B}’\] cùng ở trong một mặt phẳng.
[D]. $O{O}’$ là đường trung bình của hình bình hành \[AD{C}'{B}’\].
Chọn [C].
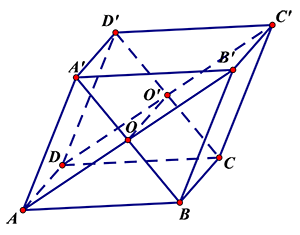
$AD{C}'{B}’$ là hình bình hành có $O{O}’$ là đường trung bình nên \[\overrightarrow{O{O}’}=\overrightarrow{AD}\]. Đáp án A, D đúng.
$O{O}’\text{//}AD$ nên $O{O}’\text{//}\left( AD{D}'{A}’ \right)$. Đáp án B đúng.
Câu 20: Cho hình hộp \[ABCD.{A}'{B}'{C}'{D}’\]. Gọi $I$ là trung điểm \[AB\]. Mp\[\left( I{B}'{D}’ \right)\] cắt hình hộp theo thiết diện là hình gì?
[A]. Tam giác.
[B]. Hình thang.
[C]. Hình bình hành.
[D]. Hình chữ nhật.
Chọn [B].
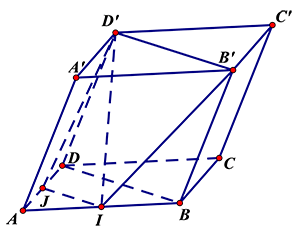
$\left( I{B}'{D}’ \right)\cap \left( A{A}'{B}’B \right)=I{B}’$.
$\left( I{B}'{D}’ \right)\cap \left( {A}'{B}'{C}'{D}’ \right)={B}'{D}’$.
$\left. \begin{align}
& I\in \left( I{B}'{D}’ \right)\cap \left( ABCD \right) \\
& {B}'{D}’\text{//}BD \\
& {B}'{D}’\subset \left( {A}'{B}'{C}'{D}’ \right) \\
& BD\subset \left( ABCD \right) \\
\end{align} \right\}$$\Rightarrow \left( I{B}'{D}’ \right)\cap \left( ABCD \right)=d$ với $d$ là đường thẳng qua $I$và song song với $BD$.
Gọi $J$ là trung điểm của $AD$.
Khi đó $\left( I{B}'{D}’ \right)\cap \left( ABCD \right)=IJ$.
$\left( I{B}'{D}’ \right)\cap \left( AD{D}'{A}’ \right)=J{D}’$.
Thiết diện cần tìm là hình thang $IJ{D}'{B}’$ với $IJ\text{//}{D}'{B}’$.
Câu 21: Cho hình lăng trụ \[ABC.{A}'{B}'{C}’\]. Gọi \[M,{M}’\] lần lượt là trung điểm của \[BC\] và\[{B}'{C}’\]. \[G,{G}’\] lần lượt là trọng tâm tam giác \[ABC\] và\[{A}'{B}'{C}’\]. Bốn điểm nào sau đây đồng phẳng?
[A]. \[A,G,{G}’,{C}’\].
[B]. \[A,G,{M}’,{B}’\].
[C]. \[{A}’,{G}’,M,C\].
[D]. \[A,{G}’,{M}’,G\].
Chọn [D].
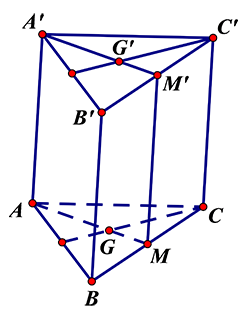
$M{M}’$ là đường trung bình trong hình bình hành $B{B}'{C}’C$ nên $M{M}’=B{B}’=A{A}’;M{M}’\,\text{//}\,B{B}’\,\text{//}\,A{A}’$
Do đó $A{A}'{M}’M$ là hình bình hành hay 4 điểm \[A,{G}’,{M}’,G\] đồng phẳng.
Câu 22: Cho hình lăng trụ \[ABC.{A}'{B}'{C}’\]. Gọi \[M,N\] lần lượt là trung điểm của \[B{B}’\] và\[C{C}’\],\[\Delta =\text{ }mp\left( AMN \right)\cap mp\left( {A}'{B}'{C}’ \right)\]. Khẳng định nào sau đây đúng ?
[A]. \[\Delta \text{// }AB\].
[B]. \[\Delta \text{// }AC\].
[C]. \[\Delta \text{// }BC\].
[D]. \[\Delta \text{//}A{A}’\].
Chọn [C].
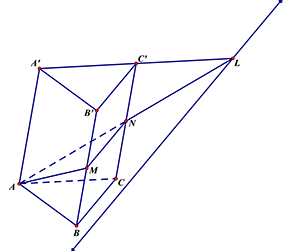
$MN$ là đường trung bình trong hình bình hành $BC{C}'{B}’$ nên $MN\text{//}{B}'{C}’$
\[\begin{align}
& \Delta =\text{ }mp\left( AMN \right)\cap mp\left( {A}'{B}'{C}’ \right) \\
& MN\subset \left( AMN \right) \\
& {B}'{C}’\subset \left( {A}'{B}'{C}’ \right) \\
\end{align}\]
Do đó $\Delta \text{//}BC$.
Câu 23: Cho hình hộp \[ABCD.{A}'{B}'{C}'{D}’\] có các cạnh bên\[A{A}’,B{B}’,C{C}’,D{D}’\]. Khẳng định nào sai ?
[A]. \[\left( A{A}'{B}’B \right)\text{//}\left( D{D}'{C}’C \right)\].
[B]. \[\left( B{A}'{D}’ \right)\] và \[\left( AD{C}’ \right)\] cắt nhau.
[C]. \[{A}'{B}’CD\] là hình bình hành.
[D]. \[B{B}’DC\] là một tứ giác đều.
Chọn [D]
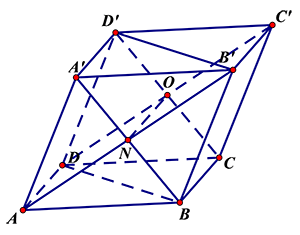
Câu A, C đúng do tính chất của hình hộp.
$\left( B{A}'{D}’ \right)\equiv \left( B{A}'{D}’C \right);\left( AD{C}’ \right)\equiv \left( AD{C}'{B}’ \right)$
\[\left( B{A}'{D}’ \right)\]\[\cap \left( AD{C}’ \right)=ON\]. Câu B đúng.
Do \[{B}’\notin \left( BDC \right)\] nên \[B{B}’DC\] không phải là tứ giác.
Câu 24: Cho hình lăng trụ \[ABC.{A}'{B}'{C}’\]. Gọi \[H\] là trung điểm của \[{A}'{B}’\]. Đường thẳng \[{B}’C\] song song với mặt phẳng nào sau đây ?
[A]. \[\left( AH{C}’ \right)\].
[B]. \[\left( A{A}’H \right)\].
[C]. \[\left( HAB \right)\].
[D]. \[\left( H{A}'{C}’ \right)\].
Chọn [A].
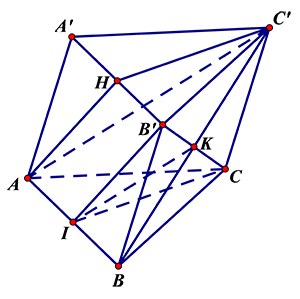
Gọi $K$ là giao điểm của ${B}’C$ và $B{C}’$, $I$ là trung điểm của $AB$.
Do $H{B}’=AI;H{B}’\text{//}AI$ nên $AH{B}’I$ là hình bình hành hay $AH\text{//}{B}’I$.
Mặt khác $KI\text{//}A{C}’$ nên $\left( AH{C}’ \right)\text{//}\left( {B}’CI \right)$.
Khi đó : ${B}’C\text{//}\left( AH{C}’ \right)$
Câu 25: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}’\]. Mp$\left( \alpha \right)$ đi qua một cạnh của hình hộp và cắt hình hộp theo thiết diện là một tứ giác \[\left( T \right)\]. Khẳng định nào sau đây là đúng ?
[A]. \[\left( T \right)\] là hình chữ nhật.
[B]. \[\left( T \right)\] là hình bình hành.
[C]. \[\left( T \right)\] là hình thoi.
[D]. \[\left( T \right)\] là hình vuông.
Chọn [B]
DẠNG 2: XÁC ĐỊNH THIẾT DIỆN CỦA \[\left( \alpha \right)\] VỚI HÌNH CHÓP KHI BIẾT \[\left( \alpha \right)\] VỚI MỘT MẶT PHẲNG \[\left( \beta \right)\] CHO TRƯỚC.
Phương pháp:
– Để xác định thiết diện trong trường hợp này ta sử dụng các tính chất sau.
– Khi \[\left( \alpha \right)\parallel \left( \beta \right)\]thì \[\left( \alpha \right)\] sẽ song song với tất cả các đường thẳng trong \[\left( \beta \right)\]và ta chuyển về dạng thiết diện song song với đường thẳng (§3)
Sử dụng \[\left\{ \begin{align}
& \left( \alpha \right)\parallel \left( \beta \right) \\
& \left( \beta \right)\parallel \left( \gamma \right) \\
& \left( \beta \right)\cap \left( \gamma \right)=d \\
& M\in \left( \alpha \right)\cap \left( \gamma \right) \\
\end{align} \right.\]\[\Rightarrow \left( \alpha \right)\cap \left( \gamma \right)=d’\parallel d,M\in d’\].
– Tìm đường thẳng \[d\] mằn trong \[\left( \beta \right)\] và xét các mặt phẳng có trong hình chóp mà chứa \[d\], khi đó \[\left( \alpha \right)\parallel d\] nên sẽ cắt các mặt phẳng chứa \[d\]( nếu có) theo các giao tuyến song song với \[d\].
Câu 26: Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành và \[M,N\] lần lượt là trung điểm của \[AB,CD\]. Xác định thiết diện của hình chóp cắt bởi \[\left( \alpha \right)\] đi qua \[MN\] và song song với mặt phẳng \[\left( SAD \right)\].Thiết diện là hình gì?
[A]. Tam giác
[B]. Hình thang
[C]. Hình bình hành
[D]. Tứ giác

Ta có \[\left\{ \begin{align}
& M\in \left( SAB \right)\cap \left( \alpha \right) \\
& \left( SAB \right)\cap \left( SAD \right)=SA \\
\end{align} \right.\]\[\Rightarrow \left( SAB \right)\cap \left( \alpha \right)=MK\parallel SA,K\in SB\].
Tương tự \[\left\{ \begin{align}
& N\in \left( SCD \right)\cap \left( \alpha \right) \\
& \left( \alpha \right)\parallel \left( SAD \right) \\
& \left( SCD \right)\cap \left( SAD \right)=SD \\
\end{align} \right.\] \[\Rightarrow \left( SCD \right)\cap \left( \alpha \right)=NH\parallel SD,H\in SC\].
Dễ thấy \[HK=\left( \alpha \right)\cap \left( SBC \right)\]. Thiết diện là tứ giác \[MNHK\]
Ba mặt phẳng \[\left( ABCD \right),\left( SBC \right)\] và \[\left( \alpha \right)\] đôi một cắt nhau theo các giao tuyến là \[MN,HK,BC\], mà \[MN\parallel BC\Rightarrow MN\parallel HK\]. Vậy thiết diện là một hình thang.
Câu 27: Cho hìh chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\] có \[AC=a,BD=b\]. Tam giác \[SBD\] là tam giác đều. Một mặt phẳng \[\left( \alpha \right)\] di động song song với mặt phẳng \[\left( SBD \right)\] và đi qua điểm \[I\] trên đoạn \[AC\]và \[AI=x\text{ }\left( 0<x<a \right)\].
a) thiết diện của hình chóp cắt bởi \[\left( \alpha \right)\] là hình gi?
[A]. Tam giác
[B]. Tứ giác
[C]. Hình thang
[D]. Hình bình hành
b) Tính diện tích thiết diện theo \[a,b\] và \[x\].

a) Trường hợp 1 Xét \[I\] thuộc đoạn \[OA\]
Ta có \[\left\{ \begin{align}
& I\in \left( \alpha \right)\cap \left( ABD \right) \\
& \left( \alpha \right)\parallel \left( SBD \right) \\
& \left( ABD \right)\cap \left( SBD \right)=BD \\
\end{align} \right.\]
\[\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MN\parallel BD,I\in MN\].
Tương tự \[\left\{ \begin{align}
& N\in \left( \alpha \right)\cap \left( SAD \right) \\
& \left( \alpha \right)\parallel \left( SBD \right) \\
& \left( SAD \right)\cap \left( SBD \right)=SD \\
\end{align} \right.\] \[\Rightarrow \left( SAD \right)\cap \left( \alpha \right)=NP\parallel SD,P\in SN\].
Thiết diện là tam giác \[MNP\].
Do \[\left\{ \begin{align}
& \left( \alpha \right)\parallel \left( SBD \right) \\
& \left( SAB \right)\cap \left( SBD \right)=SB \\
& \left( SAB \right)\cap \left( \alpha \right)=MP \\
\end{align} \right.\Rightarrow MP\parallel SB\]. Hai tam giác \[MNP\] và \[BDS\] có các cặp cạnh tương ứng song song nên chúng đồng dạng, mà \[BDS\]đều nên tam giác \[MNP\] đều.
Trường hợp 2 Điểm \[I\] thuộc đoạn \[OC\], tương tự trường hợp 1 ta được thiết diện là tam giác đều \[HKL\] như \[\left( hv \right)\].
b) Trường hợp 1 \[I\] thuộc đoạn \[OA\]

Ta có \[{{S}_{BCD}}=\dfrac{B{{D}^{2}}\sqrt{3}}{4}=\dfrac{{{b}^{2}}\sqrt{3}}{4}\], \[\dfrac{{{S}_{MNP}}}{{{S}_{BCD}}}={{\left( \dfrac{MN}{BD} \right)}^{2}}\]
Do \[MN\parallel BD\Rightarrow \dfrac{MN}{BD}=\dfrac{AI}{AO}=\dfrac{2x}{a}\]\[\Rightarrow {{S}_{MNP}}={{\left( \dfrac{2x}{a} \right)}^{2}}{{S}_{BCD}}=\dfrac{{{b}^{2}}{{x}^{2}}\sqrt{3}}{{{a}^{2}}}\].
Trường hợp 2 \[I\] thuộc đoạn \[OC\], tính tương tự ta có
\[{{S}_{MNP}}={{\left( \dfrac{HL}{BD} \right)}^{2}}{{S}_{BCD}}={{\text{ }\!\![\!\!\text{ }\dfrac{2\left( a-x \right)}{a}\text{ }\!\!]\!\!\text{ }}^{2}}\dfrac{{{b}^{2}}\sqrt{3}}{4}=\dfrac{{{b}^{2}}{{\left( a-x \right)}^{2}}\sqrt{3}}{{{a}^{2}}}\].
Vậy \[{{S}_{td}}=\left\{ \begin{align}
& \dfrac{{{b}^{2}}{{x}^{2}}\sqrt{3}}{{{a}^{2}}};I\in (OA) \\
& \dfrac{{{b}^{2}}{{\left( a-x \right)}^{2}}\sqrt{3}}{{{a}^{2}}};I\in \left( OC \right) \\
\end{align} \right.\].
Câu 28: Cho tứ diện \[ABCD\] và \[M,N\] là các điểm thay trên các cạnh \[AB,CD\] sao cho \[\dfrac{AM}{MB}=\dfrac{CN}{ND}\].
a) Chứng minh \[MN\] luôn luôn song song với một mặt phẳng cố định.
b) Cho \[\dfrac{AM}{MB}=\dfrac{CN}{ND}>0\] và \[P\] là một điểm trên cạnh \[AC\]. thiết diện của hình chóp cắt bởi \[\left( MNP \right)\]là hình gì?
[A]. Tam giác
[B]. Tứ giác
[C]. Hình thang
[D]. Hình bình hành
c) Tính theo \[k\] tỉ số diện tích tam giác \[MNP\] và diện tích thiết diện.
[A]. $\dfrac{k}{k+1}$
[B]. $\dfrac{2k}{k+1}$
[C]. $\dfrac{1}{k}$
[D]. $\dfrac{1}{k+1}$
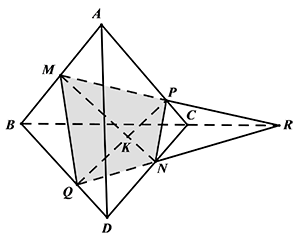
a) Do \[\dfrac{AM}{MB}=\dfrac{CN}{ND}\] nên theo định lí Thales thì các đường thẳng \[MN,AC,BD\] cùng song song với một mặt phẳng \[\left( \beta \right)\].Gọi \[\left( \alpha \right)\] là mặt phẳng đi qua \[AC\] và song song với \[BD\]thì \[\left( \alpha \right)\] cố định và \[\left( \alpha \right)\parallel \left( \beta \right)\]suy ra \[MN\] luôn song song với \[\left( \alpha \right)\] cố định.
b) Xét trường hợp \[\dfrac{AP}{PC}=k\], lúc này \[MP\parallel BC\] nên \[BC\parallel \left( MNP \right)\].
Ta có :
\[\left\{ \begin{align}
& N\in \left( MNP \right)\cap \left( BCD \right) \\
& BC\parallel \left( MNP \right) \\
& BC\subset \left( BCD \right) \\
\end{align} \right.\]\[\Rightarrow \left( BCD \right)\cap \left( MNP \right)=NQ\parallel BC,Q\in BD\].
Thiết diện là tứ giác \[MPNQ\].Xét trường hợp \[\dfrac{AP}{PC}\ne k\]
Trong \[\left( ABC \right)\]gọi \[R=BC\cap MP\]
Trong \[\left( BCD \right)\] gọi \[Q=NR\cap BD\] thì thiết diện là tứ giác \[MPNQ\].
Gọi \[K=MN\cap PQ\]
Ta có \[\dfrac{{{S}_{MNP}}}{{{S}_{MPNQ}}}=\dfrac{PK}{PQ}\].
Do \[\dfrac{AM}{NB}=\dfrac{CN}{ND}\] nên theo định lí Thales đảo thì \[AC,NM,BD\] lần lượt thuộc ba mặt phẳng song song với nhau và đường thẳng \[PQ\] cắt ba mặt phẳng này tương ứng tại \[P,K,Q\] nên áp dụng định lí Thales ta được \[\dfrac{PK}{KQ}=\dfrac{AM}{MB}=\dfrac{CN}{ND}=k\]\[\Rightarrow \dfrac{PK}{PQ}=\dfrac{PK}{PK+KQ}=\dfrac{\dfrac{PK}{KQ}}{\dfrac{PK}{KQ}+1}=\dfrac{k}{k+1}\].