Góc giữa hai đường thẳng, hai đường thẳng vuông góc, trắc nghiệm toán 11
- Định nghĩa:
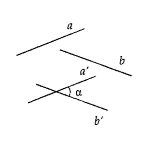
Góc giữa hai đường thẳng cắt nhau \[a\] và \[b\] là góc nhỏ nhất trong bốn góc mà \[a\] và \[b\] cắt nhau tạo nên.
Góc giữa hai đường thẳng cắt nhau \[a\] và \[b\] trong không gian là góc giữa hai đường thẳng \[{a}’\] và \[{b}’\] cùng đi qua một điểm và lần lượt song song (hoặc trùng) với \[a\] và\[b\].
Chú ý: góc giữa hai đường thẳng luôn là góc nhọn ( hoặc vuông ).
- Phương pháp
Phương pháp 1: Sử dụng định lý hàm số cosin hoặc tỉ số lượng giác.
Phương pháp 2: Sử dụng tích vô hướng: nếu \[\overrightarrow{u}\] và \[\overrightarrow{v}\] lần lượt là hai vecto chỉ phương ( hoặc vecto pháp tuyến ) của hai đường thẳng \[a\] và\[b\] thì góc \[\varphi \] của hai đường thẳng này được xác định bởi công thức
\[\cos \varphi =\left| \cos \left( \overrightarrow{u},\overrightarrow{v} \right) \right|=\dfrac{\left| \overrightarrow{u}.\overrightarrow{v} \right|}{\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|}.\]
Câu 1
Cho hình lập phương\[ABCD.{A}'{B}'{C}'{D}’\]. Gọi \[M,N,P\] lần lượt là trung điểm các cạnh\[AB\], \[BC\],\[{C}'{D}’\]. Xác định góc giữa hai đường thẳng \[MN\] và\[AP\].
[A]. \[{{45}^{0}}\].
[B]. \[{{30}^{0}}\].
[C]. \[{{60}^{0}}\].
[D]. \[{{90}^{0}}\]
Đáp án [A].
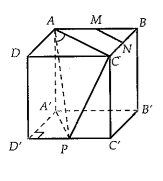
Phương pháp 1: Giả sử hình lập phương có cạnh bằng \[a\] và \[MN\text{//}AC\] nên: $\left( \widehat{MN,AP} \right)=\left( \widehat{AC,AP} \right)$. Ta tính góc $\widehat{PAC}$.
Vì \[\Delta {A}'{D}’P\] vuông tại \[{D}’\] nên ${A}’P=\sqrt{{A}'{{{{D}’}}^{2}}+{D}'{{P}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}$.
\[\Delta A{A}’P\] vuông tại \[{A}’\] nên $AP=\sqrt{{A}'{{A}^{2}}+{A}'{{P}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \dfrac{a\sqrt{5}}{2} \right)}^{2}}}=\dfrac{3a}{2}$.
\[\Delta C{C}’P\] vuông tại \[{C}’\] nên $CP=\sqrt{C{{{{C}’}}^{2}}+{C}'{{P}^{2}}}=\sqrt{{{a}^{2}}+\dfrac{{{a}^{2}}}{4}}=\dfrac{a\sqrt{5}}{2}.$
Ta có \[AC\] là đường chéo của hình vuông \[ABCD\] nên \[AC=\] $a\sqrt{2}$
Áp dụng định lý cosin trong tam giác \[ACP\] ta có:
\[\begin{align}
& C{{P}^{2}}=A{{C}^{2}}+A{{P}^{2}}-2A[C].AP.cos\widehat{CAP} \\
& \Rightarrow cos\widehat{CAP}=\dfrac{1}{\sqrt{2}} \\
& \Rightarrow cos\widehat{CAP}=45{}^\circ <90{}^\circ \\
\end{align}\]
Nên $\left( \widehat{AC;AP} \right)=\widehat{CAP}=45{}^\circ $ hay \[\left( \widehat{MN;AP} \right)=45{}^\circ \]. Chọn [A].
Phương pháp 2: Ta có $\overrightarrow{MN}.\overrightarrow{AP}=\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AP} \right|.\cos \left( \overrightarrow{MN},\overrightarrow{AP} \right)$$\Rightarrow \cos \left( \overrightarrow{MN},\overrightarrow{AP} \right)=\dfrac{\overrightarrow{MN}.\overrightarrow{AP}}{\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AP} \right|}\,\,\left( * \right)$
Ta có: $\overrightarrow{MN}.\overrightarrow{AP}=\left( \overrightarrow{MB}+\overrightarrow{BN} \right)\left( \overrightarrow{A{A}’}+\overrightarrow{{A}'{D}’}+\overrightarrow{{D}’P} \right)$
$=\overrightarrow{MB}.\overrightarrow{A{A}’}+\overrightarrow{MB}.\overrightarrow{{A}'{D}’}+\overrightarrow{MB}.\overrightarrow{{D}’P}+\overrightarrow{BN}.\overrightarrow{A{A}’}+\overrightarrow{BN}.\overrightarrow{{A}'{D}’}+\overrightarrow{BN}.\overrightarrow{{D}’P}$
$=0+0+\dfrac{a}{2}.\dfrac{a}{2}+0+\dfrac{a}{2}.a+0=\dfrac{3{{a}^{2}}}{4}\left( 1 \right)$
$\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AP} \right|=\dfrac{a\sqrt{2}}{2}.\dfrac{3a}{2}=\dfrac{3\sqrt{2}{{a}^{2}}}{4}\left( 2 \right)$
Thay $\left( 1 \right),\left( 2 \right)$ vào $\left( * \right)$ ta được: $\cos \left( \overrightarrow{MN},\overrightarrow{AP} \right)=\dfrac{\dfrac{3{{a}^{2}}}{4}}{\dfrac{3\sqrt{2}{{a}^{2}}}{4}}=\dfrac{1}{\sqrt{2}}\Rightarrow \widehat{\left( MN,AP \right)}={{45}^{0}}.$
Câu 2
Cho tứ diện $ABCD$ có $AB=CD=2a.$ Gọi $M,N$ lần lượt là trung điểm $BC,AD$. Biết rằng $MN=a\sqrt{3}.$ Tính góc của $AB$ và $CD$.
[A]. ${{45}^{0}}.$
[B]. ${{30}^{0}}$.
[C]. ${{60}^{0}}$.
[D]. ${{90}^{0}}$.
Đáp án [C].
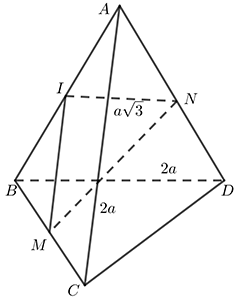
Gọi $I$ là trung điểm của $AC$. Ta có $IM=IN=a$.
Áp dụng định lý cosin cho $\Delta IMN$ ta có:
$\cos \widehat{MIN}=\dfrac{I{{M}^{2}}+I{{N}^{2}}-M{{N}^{2}}}{2.IM.IN}=\dfrac{{{a}^{2}}+{{a}^{2}}-3{{a}^{2}}}{2.a.a}=-\dfrac{1}{2}\Rightarrow \widehat{MIN}={{120}^{0}}$.
Vì $IM//AB,IN//CD\Rightarrow \widehat{\left( AB,CD \right)}=\widehat{\left( IM,IN \right)}={{180}^{0}}-{{120}^{0}}={{60}^{0}}$.
Câu 3
Cho lăng trụ $ABC{A}'{B}'{C}’$ có độ dài cạnh bên bằng $2a$, đáy $ABC$ là tam giác vuông tại $A\,$, $AB=a$, $AC=a\sqrt{3}$ và hình chiếu vuông góc của đỉnh ${A}’$ trên mặt phẳng $\left( ABC \right)$ là trung điểm của cạnh $BC$. Tính cosin của góc giữa hai đường thẳng $A{A}’$, ${B}'{C}’$.
Phương pháp 1:
Gọi $H$ là trung điểm của $BC$, $\varphi $ là góc giữa $A{A}’$ và ${B}'{C}’$.
Ta có $A{A}’//B{B}’$ và ${B}'{C}’//BC$ nên góc giữa $\left( \widehat{A{A}’,{B}'{C}’} \right)=\left( \widehat{B{B}’,BC} \right)$ .
Ta tính góc $\widehat{\,{B}’BH}$
$\Delta ABC$ vuông tại $A$ nên ta có: $BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a$.
$AH=\dfrac{1}{2}BC=a\Rightarrow {A}’H=\sqrt{A{{{{A}’}}^{2}}-A{{H}^{2}}}=\sqrt{4{{a}^{2}}-{{a}^{2}}}=a\sqrt{3}$.
Vì $AH\bot \left( {A}'{B}'{C}’ \right)$ nên $\Delta {A}'{B}’H$ vuông tại ${A}’$
${B}’H=\sqrt{{A}'{{H}^{2}}+{A}'{{{{B}’}}^{2}}}=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a$.
\[\cos \widehat{{B}’BH}=\dfrac{{B}'{{B}^{2}}+B{{H}^{2}}-{B}'{{H}^{2}}}{2{B}’B.BH}\]
\[=\dfrac{4{{a}^{2}}+{{a}^{2}}-4{{a}^{2}}}{2.2a.a}=\dfrac{1}{4}\] Chọn A
Phương pháp 2:
Ta có
\[\cos \varphi =\left| \cos \left( \overrightarrow{A{A}’};\overrightarrow{{B}'{C}’} \right) \right|=\dfrac{\left| \overrightarrow{A{A}’}.\overrightarrow{{B}'{C}’} \right|}{\left| \overrightarrow{A{A}’} \right|.\left| \overrightarrow{{B}'{C}’} \right|}=\dfrac{\left| \left( \overrightarrow{AH}+\overrightarrow{H{A}’} \right).\overrightarrow{BC} \right|}{2a.2a}=\dfrac{\left| \overrightarrow{AH}.\overrightarrow{BC}+\overrightarrow{H{A}’}.\overrightarrow{BC} \right|}{4{{a}^{2}}}=\dfrac{\left| \overrightarrow{AH}.\overrightarrow{BC} \right|}{4{{a}^{2}}}\]
$=\dfrac{\left| \dfrac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right)\left( \overrightarrow{AC}-\overrightarrow{AB} \right) \right|}{4{{a}^{2}}}=\dfrac{\left| \dfrac{1}{2}\left( A{{C}^{2}}-A{{B}^{2}} \right) \right|}{4{{a}^{2}}}=\dfrac{\left| \dfrac{1}{2}\left( 3{{a}^{2}}-{{a}^{2}} \right) \right|}{4{{a}^{2}}}=\dfrac{1}{4}$.
Câu 4
Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$. Gọi \[M\] là trung điểm $CD$. Tính cosin góc của $AC$ và $BM$.
[A]. $\dfrac{\sqrt{3}}{4}$ .
[B]. $\dfrac{\sqrt{3}}{6}$.
[C]. $\dfrac{\sqrt{3}}{2}$.
[D]. $\dfrac{\sqrt{2}}{2}$.
Chọn B
Cách 1. Gọi \[N\] là trung điểm \[AD\] ta có: $MN\text{//}AC$ $\Rightarrow \left( \,\widehat{AC;BM} \right)=\,\left( \,\widehat{MN;BM} \right)$. Ta tính góc$\,\widehat{BMN}$. Ta có: $BM=BN=\dfrac{a\sqrt{3}}{2}$ (trung tuyến tam giác đều).
$MN=\dfrac{AC}{2}=\dfrac{a}{2}$.
Áp dụng định lý cosin cho $\Delta BMN$, ta được:
$\cos \,\widehat{BMN}=\dfrac{B{{M}^{2}}+M{{N}^{2}}-B{{N}^{2}}}{2BM.MN}=\dfrac{MN}{2BM}=\dfrac{\sqrt{3}}{6}>0$.
Vậy $\cos \left( \,\widehat{AC;BM} \right)=\dfrac{\sqrt{3}}{6}.$
Cách 2. $\cos \varphi =\left| \cos \left( \overrightarrow{AC},\overrightarrow{BM} \right) \right|=\dfrac{\left| \overrightarrow{AC}.\overrightarrow{BM} \right|}{\left| \overrightarrow{AC} \right|.\left| \overrightarrow{BM} \right|}=\dfrac{\left| \overrightarrow{AC}.\left( \overrightarrow{CM}-\overrightarrow{CB} \right) \right|}{a.\dfrac{a\sqrt{3}}{2}}$
$=\dfrac{\left| \overrightarrow{AC}.\overrightarrow{CM}-\overrightarrow{AC}.\overrightarrow{CB} \right|}{\dfrac{{{a}^{2}}\sqrt{3}}{2}}=\dfrac{\left| a.\dfrac{a}{2}\cos {{120}^{0}}-a.a.\cos {{120}^{0}} \right|}{\dfrac{{{a}^{2}}\sqrt{3}}{2}}=\dfrac{\left| -\dfrac{{{a}^{2}}}{4}+\dfrac{{{a}^{2}}}{2} \right|}{\dfrac{{{a}^{2}}\sqrt{3}}{2}}=\dfrac{\dfrac{{{a}^{2}}}{4}}{\dfrac{{{a}^{2}}\sqrt{3}}{2}}=\dfrac{\sqrt{3}}{6}$.