Véc tơ trong không gian, trắc nghiệm toán 11
Câu 1
Cho \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\]là hình hộp, với K là trung điểm CC1. Tìm khẳng định đúng trong các khẳng định sau:
[A]. \[\overrightarrow{AK}=\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
[B].\[\overrightarrow{AK}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{A{{A}_{1}}}\]
[C]. \[\overrightarrow{AK}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{{A}_{1}}}\]
[D].\[\overrightarrow{AK}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
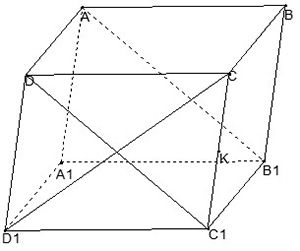
Có \[\overrightarrow{AK}=\overrightarrow{AC}+\overrightarrow{CK}=(\overrightarrow{AB}+\overrightarrow{AD})+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}=\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
Chọn A
Câu 2
Cho hình hộp \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\] với \[M=C{{D}_{1}}\cap {{C}_{1}}D\]. Khi đó:
[A]. \[\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
[B].\[\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
[C]. \[\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
[D].\[\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}+\overrightarrow{A{{A}_{1}}}\]
( hính vẽ câu 1)
Ta có: \[\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\overrightarrow{D{{C}_{1}}}=AD+\dfrac{1}{2}(\overrightarrow{DC}+\overrightarrow{\text{D}{{\text{D}}_{1}}})=\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{A{{A}_{1}}}\]
Chọn B
Câu 3
Cho hình hộp \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\] . Khi đó: tổng 3 góc \[(\overrightarrow{{{D}_{1}}{{A}_{1}}},\overrightarrow{C{{C}_{1}}})+(\overrightarrow{{{C}_{1}}B},\overrightarrow{D{{D}_{1}}})+(\overrightarrow{D{{C}_{1}}},\overrightarrow{{{A}_{1}}B})\]là:
[A]. 1800
[B]. 2900
[C].3600
[D]. 3150
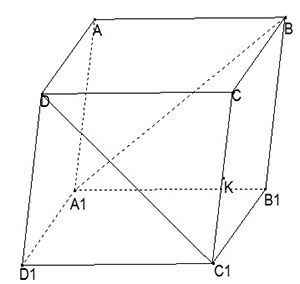
Ta có:
\[\begin{align}
& (\overrightarrow{{{D}_{1}}{{A}_{1}}},\overrightarrow{C{{C}_{1}}})={{90}^{0}} \\
& (\overrightarrow{{{C}_{1}}B},\overrightarrow{D{{D}_{1}}})=(\overrightarrow{{{C}_{1}}B},\overrightarrow{C{{C}_{1}}})={{135}^{0}} \\
& (\overrightarrow{D{{C}_{1}}},\overrightarrow{{{A}_{1}}B})=(\overrightarrow{D{{C}_{1}}},\overrightarrow{{{D}_{1}}C})={{90}^{0}} \\
\end{align}\]
\[\Rightarrow (\overrightarrow{{{D}_{1}}{{A}_{1}}},\overrightarrow{C{{C}_{1}}})+(\overrightarrow{{{C}_{1}}B},\overrightarrow{D{{D}_{1}}})+(\overrightarrow{D{{C}_{1}}},\overrightarrow{{{A}_{1}}B})={{90}^{0}}+{{135}^{0}}+{{90}^{0}}={{315}^{0}}\]
Chọn D
Câu 4
Cho hình lập phương \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\], đặt \[\alpha =(\overrightarrow{AC},\overrightarrow{D{{C}_{1}}});\,\,\,\beta =(\overrightarrow{D{{A}_{1}}},\overrightarrow{B{{B}_{1}}});\,\,\gamma =(\overrightarrow{A{{A}_{1}}},\overrightarrow{{{C}_{1}}C})\] Khi đó: là\[\alpha +\,\,\beta +\,\,\gamma \]:
[A]. 3600
[B]. 3750
[C]. 3150
[D]. 2750

\[\alpha =(\overrightarrow{AC},\overrightarrow{D{{C}_{1}}})=(\overrightarrow{AC},\overrightarrow{A{{B}_{1}}})={{60}^{0}}\]
\[\beta =(\overrightarrow{D{{A}_{1}}},\overrightarrow{B{{B}_{1}}})=(\overrightarrow{D{{A}_{1}}},\overrightarrow{{{A}_{1}}A})={{135}^{0}}\]
\[\gamma =(\overrightarrow{A{{A}_{1}}},\overrightarrow{{{C}_{1}}C})=(\overrightarrow{A{{A}_{1}}},\overrightarrow{{{A}_{1}}A})={{180}^{0}}\]
\[\Rightarrow \alpha +\beta +\gamma ={{60}^{0}}+{{135}^{0}}+{{180}^{0}}={{375}^{0}}\]
Chọn B
Câu 5
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB=6; AD=4;\[\overrightarrow{AB}.\overrightarrow{AD}=12\] . Tính \[{{(\overrightarrow{SC}.-\overrightarrow{SA})}^{2}}.\]
[A]. 76
[B]. 28
[C]. 52
[D]. 40
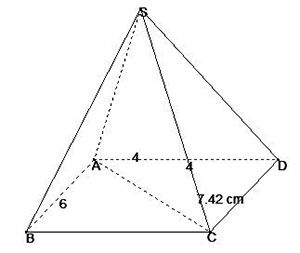
\[{{(\overrightarrow{SC}.-\overrightarrow{SA})}^{2}}.={{\overrightarrow{AC}}^{2}}=(\overrightarrow{AB}+\overrightarrow{AD})={{\overrightarrow{AB}}^{2}}+{{\overrightarrow{AD}}^{2}}+2\overrightarrow{AB}.\overrightarrow{AD}\]
\[={{6}^{2}}+{{4}^{2}}+2(-12)=28\]
Chọn B
Câu 6
Chỉ ra mệnh đề đúng trong các mệnh đề sau:
[A]. Ba vectơ đồng phẳng là 3 vec tơ cùng nằm trong một mặt phẳng
[B]. Ba vectơ \[\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}\] đồng phẳng thì có \[\overrightarrow{c}=m\overrightarrow{a}+n\,\overrightarrow{b},\,\]với m, n là các số duy nhất
[C]. Ba vectơ đồng phẳng khi có \[\overrightarrow{d}=m\overrightarrow{a}+n\,\overrightarrow{b}+p\overrightarrow{c}\,\]với \[\overrightarrow{d}\] là vec tơ bất kỳ
[D]. Cả 3 mệnh đề trên đều sai
-Phương án A: sai vi chỉ cần giá của chúng song song hoặc nằm trên một mặt phẳng nào đó
Phương án B: Sai \[\overrightarrow{a},\,\,\overrightarrow{b}\] phải không cùng phương.
Phương án C sai
Vậy chọn D
Câu 7
Cho hình tứ diện ABCD, trọng tâm G. Mệnh đề nào sau đây sai?
[A]. \[\overrightarrow{OG}=\dfrac{1}{4}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})\,\,\]
[B]. \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\]
[C]. \[\overrightarrow{AG}=\dfrac{2}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})\]
[D]. \[\overrightarrow{AG}=\dfrac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})\]
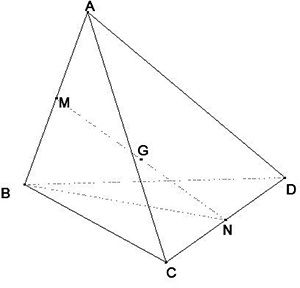
Gọi M, N lần lượt là trung điểm của AB, CD
\[\Rightarrow \] G là trung điểm của MN \[\Rightarrow \overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{0}\]
\[\Leftrightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\] \[\Rightarrow \]B đúng
Ta có: \[\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OG}+\overrightarrow{GA}+\overrightarrow{OG}+\overrightarrow{GB}+\overrightarrow{OG}+\overrightarrow{GC}+\overrightarrow{OG}+\overrightarrow{GD}\]
\[=4\overrightarrow{OG}+(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD})=4\overrightarrow{OG}\] \[\Rightarrow \]A đúng
Khi O trùng A thì D đúng vậy đáp án là [C].
Câu 8
Cho ba vectơ \[\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}\] không đồng phẳng xét các vectơ\[\overrightarrow{x}=2\overrightarrow{a}-\overrightarrow{b};\,\overrightarrow{y}=-4\overrightarrow{a}+2\overrightarrow{b};\,\,\overrightarrow{z}=-3\overrightarrow{a}-2\overrightarrow{c}\] Chọn mênh đề đúng trong các mệnh đề sau:
[A].Hai vec tơ\[\overrightarrow{y},\,\overleftarrow{z}\] cùng phương
[B]. Hai vec tơ\[\overrightarrow{x},\,\overleftarrow{y}\] cùng phương
[C].Hai vec tơ\[\overrightarrow{x},\,\overleftarrow{z}\] cùng phương
[D].Hai vec tơ\[\overrightarrow{x},\overrightarrow{y},\,\overleftarrow{z}\] đồng phẳng
Ta thấy \[\overrightarrow{y}=-2\overrightarrow{x}\] nên \[\overrightarrow{x},\,\overrightarrow{y}\] cùng phương.
Chọn B
Câu 9
Cho hình lập phương \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\], Tìm giá trị của k thích hợp để\[\overrightarrow{AB}\,\,+\overrightarrow{{{B}_{1}}{{C}_{1}}}+\overrightarrow{D{{D}_{1}}}=k\overrightarrow{A{{C}_{1}}})\]
[A].k=4
[B]. k=1
[C]. k=0
[D]. k=2
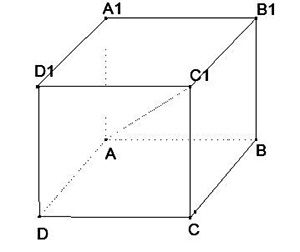
Có \[\underrightarrow{AB}+\overrightarrow{{{B}_{1}}{{C}_{1}}}+\overrightarrow{\text{D}{{\text{D}}_{1}}}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C{{C}_{1}}}=\overrightarrow{A{{C}_{1}}}\Rightarrow k=1\]
Chọn B
Câu 10
Cho hình lăng trụ tam giác \[ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\]. Đặt \[\overrightarrow{\text{A}{{\text{A}}_{1}}}=a;\,\,\overrightarrow{\text{AB}}=b;\,\overrightarrow{\text{AC}}=c;\,\,\overrightarrow{B{{C}_{1}}}=d\] trong các đẳng thức sau đẳng thức nào đúng.
[A].\[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{0}\]
[B]. \[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{d}\]
[C]. \[\overrightarrow{b}-\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{0}\]
[D]. \[\overrightarrow{a}=\overrightarrow{b}+\overrightarrow{c}\] \[\]
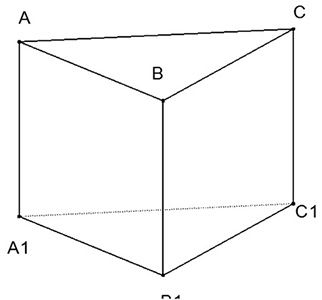
Ta có: \[\overrightarrow{b}-\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BC}=\overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}\]
Chọn C
Câu 11
Trong các khẳng định sau đây, khẳng định nào sai?
[A].Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng
[B].Nếu ba vectơ \[\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}\]có một vec tơ \[\overrightarrow{0}\] thì ba vectơ đồng phẳng
[C].Nếu giá của ba vectơ \[\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}\] cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng
[D].Nếu trong ba vectơ \[\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}\] có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng
Chọn A
Câu 12
Cho \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\]là hình hộp, trong các khẳng định sau khẳng định sai:
[A].\[\overrightarrow{A{{C}_{1}}}+\overrightarrow{{{A}_{1}}C}=2\overrightarrow{AC}\]
[B]. \[\overrightarrow{A{{C}_{1}}}+\overrightarrow{C{{A}_{1}}}+2\overrightarrow{C{{C}_{1}}}=\overrightarrow{0}\]
[C]. \[\overrightarrow{A{{C}_{1}}}+\overrightarrow{{{A}_{1}}C}=\overrightarrow{A{{A}_{1}}}\]
[D]. \[\overrightarrow{C{{A}_{1}}}+\overrightarrow{AC}=\overrightarrow{C{{C}_{1}}}\]
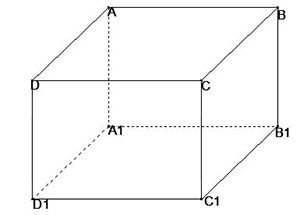
Ta có:
\[\overrightarrow{A{{C}_{1}}}+\overrightarrow{{{A}_{1}}C}=\overrightarrow{\text{A}{{\text{A}}_{1}}}\] \[\overrightarrow{A{{C}_{1}}}=\overrightarrow{\text{A}{{\text{A}}_{1}}}-\overrightarrow{A{{C}_{1}}}\Leftrightarrow \overrightarrow{{{A}_{1}}C}=\overrightarrow{{{C}_{1}}{{A}_{1}}}\]
Chọn C
Câu 13
Hãy chọn mệnh đề đúng trong các mệnh đề sau:
[A].Tứ giác ABCD là hình bình hành nếu \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0}\]
[B]. Tứ giác ABCD là hình bình hành nếu \[\overrightarrow{AB}=\overrightarrow{CD}\]
[C]. Cho hình chóp S.ABCD, nếu có \[\overrightarrow{SB}+\overrightarrow{SD}=\overrightarrow{SA}+\overrightarrow{SC}\] thì tứ giác ABCD là hình bình hành
[D].Tứ giác ABCD là hình bình hành nếu \[\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\]
Chọn C
Câu 14
Cho hình hộp \[ABCD.{{A}^{‘}}{{B}^{‘}}{{C}^{‘}}{{D}^{‘}}\] Gọi I, K lần lượt là tâm của các hình bình hành\[AB{{B}^{‘}}{{A}^{‘}}\] và \[BC{{C}^{‘}}{{B}^{‘}}\] . Khẳng định nào sau đây là sai?
[A].Bốn điểm I, K, C, A đồng phẳng
[B].\[\overrightarrow{IK}=\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{{{A}^{‘}}{{C}^{‘}}}\]
[C].Bà vec tơ \[\overrightarrow{BD},\overrightarrow{IK},\,\overrightarrow{B’C’}\] không đồng phẳng
[D].\[\overrightarrow{BD}+2\overrightarrow{IK}=2\overrightarrow{BC}\]
Chọn C
Câu 15
Cho tứ diện ABCD. Trên các cạnh AC, BD lần lượt lấy M, Nsao cho AM=3MD; BN=3NC. Gọi P,Q lần lượt là trung điểm của AD, BC. Trong các khẳng định sau, khẳng định nào sai?
[A].Các vec tơ\[\overrightarrow{BD},\,\,\overrightarrow{AC},\,\overrightarrow{MN}\] không đồng phẳng
[B]. Các vec tơ \[\overrightarrow{MN},\,\,\overrightarrow{DC},\,\overrightarrow{PQ}\] đồng phẳng
[C]. Các vec tơ \[\overrightarrow{AB},\,\,\overrightarrow{DC},\,\overrightarrow{PQ}\] đồng phẳng
[D]. Các vec tơ \[\overrightarrow{AC},\,\,\overrightarrow{DC},\,\overrightarrow{MN}\] đồng phẳng
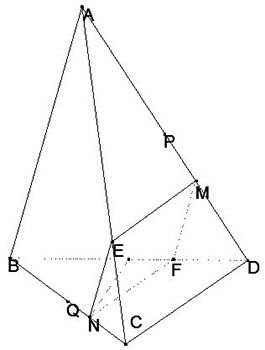
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD
\[\left\{ \begin{align}
& NE//AB,NE=\dfrac{1}{3}AB \\
& MF//AB,MF=\dfrac{1}{3}AB \\
\end{align} \right.\]\[\Rightarrow NE//MF,NE//MF\]
\[\Rightarrow \] NEMF là hình bình hành và 3 vec tơ \[\overrightarrow{BA},\,\overrightarrow{DC},\,\overrightarrow{MN}\] có giá song song hoặc nằm trên mặt phẳng (MFNE) \[\Rightarrow \]\[\overrightarrow{BA},\,\overrightarrow{DC},\,\overrightarrow{MN}\] đồng phẳng
\[\Rightarrow \]\[\overrightarrow{BD},\,\overrightarrow{AC},\,\overrightarrow{MN}\] không đồng phẳng.
Chon A
Câu 16
Cho tứ diện ABCD có các cạnh đầu bằng a. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau:
[A].\[\overrightarrow{AD}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}=\overrightarrow{0}\]
[B].\[\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{{{a}^{2}}\sqrt{3}}{2}\]
[C].\[\overrightarrow{AC}.\overrightarrow{AD}=\overrightarrow{AC}.\overrightarrow{CD}\]
[D].\[\overrightarrow{AD}.\overrightarrow{CD}=0\]

Phương án A:
\[\overrightarrow{\text{AD}}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}=(\overrightarrow{AD}+\overrightarrow{DA})+(\overrightarrow{BC}+\overrightarrow{CD})=\overrightarrow{0}+\overrightarrow{BD}\ne \overrightarrow{0}\Rightarrow \,A\] sai
Phương án B:\[\overrightarrow{AB}.\overrightarrow{AC}=a.a.c\text{os6}{{\text{0}}^{0}}\text{=}{{\dfrac{a}{2}}^{2}}\Rightarrow B\] sai
Phương án B \[\overrightarrow{AC}.\overrightarrow{AD}=\overrightarrow{AC}.\overrightarrow{CD}\Leftrightarrow \overrightarrow{AC}(\overrightarrow{AD}+\overrightarrow{DC})=0\Leftrightarrow {{\overrightarrow{AC}}^{2}}=0\Rightarrow C\] sai
Chọn D
Câu 17
Cho hình lập phương \[ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\] . Gọi M là trung điểm của AD.Chọn khẳng định đúng:
[A].\[\overrightarrow{{{B}_{1}}M}=\overrightarrow{{{B}_{1}}B}+\overrightarrow{{{B}_{1}}A{}_{1}}+\overrightarrow{{{B}_{1}}{{C}_{1}}}\]
[B]. \[\overrightarrow{{{C}_{1}}M}=\overrightarrow{{{C}_{1}}C}+\overrightarrow{{{C}_{1}}D{}_{1}}+\dfrac{1}{2}\overrightarrow{{{C}_{1}}{{B}_{1}}}\]
[C].\[\overrightarrow{{{C}_{1}}M}=\overrightarrow{{{C}_{1}}C}+\dfrac{1}{2}\overrightarrow{{{C}_{1}}D{}_{1}}+\dfrac{1}{2}\overrightarrow{{{C}_{1}}{{B}_{1}}}\]
[D]. \[\overrightarrow{B{{B}_{1}}}+\overrightarrow{{{B}_{1}}{{A}_{1}}}+\overrightarrow{{{B}_{1}}C{}_{1}}=2\overrightarrow{{{B}_{1}}D}\]
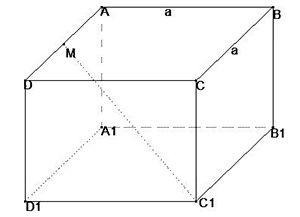
Ta có \[\overrightarrow{{{C}_{1}}M}=\overrightarrow{{{C}_{1}}{{D}_{1}}}+\overrightarrow{{{\text{D}}_{1}}\text{D}}+\overrightarrow{DM}=\overrightarrow{{{C}_{1}}{{D}_{1}}}+\overrightarrow{{{C}_{1}}C}+\dfrac{1}{2}\overrightarrow{{{C}_{1}}{{B}_{1}}}\]
Chọn B
Câu 18
Cho tứ diện ABCD và điểm G thỏa \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\] ( G là trọng tâm của tứ diện). Gọi O là giao điểm của GA và mặt phẳng (BCD) . Trong các khẳng định sau, khẳng định nào sai?
[A].\[\overrightarrow{GA}=-2\overrightarrow{OG}\]
[B]. \[\overrightarrow{GA}=4\overrightarrow{OG}\]
[C]. \[\overrightarrow{GA}=3\overrightarrow{OG}\]
[D]. \[\overrightarrow{GA}=2\overrightarrow{OG}\]
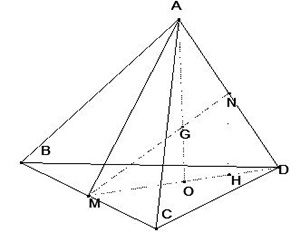
Gọi M, N là trung điểm của BC, AD
\[\Rightarrow \] G là trung điểm MN. Gọi H là hình chiếu của N lên MD \[\Rightarrow \] NH là đường trung bình của \[\Delta AOD\]và OG là đường trung bình của \[\Delta MNH\]
\[\begin{align}
& \Rightarrow OG=\dfrac{1}{2}NH=\dfrac{1}{2}.\dfrac{1}{2}AO\Rightarrow OG=\dfrac{1}{2}NH=\dfrac{1}{4}.AO \\
& hay\,\,\overrightarrow{GA}=3\overrightarrow{OG} \\
\end{align}\]
Chọn C
Câu 19
Cho tứ diện ABCD. Gọi M, Nlaafn lượt là trung điểm của AD, BC. Trong ccs khẳng định sau, khẳng định nào sai?
[A].Các vec tơ\[\overrightarrow{AB},\,\,\overrightarrow{DC},\,\overrightarrow{MN}\] đồng phẳng
[B]. Các vec tơ \[\overrightarrow{MN},\,\,\overrightarrow{AB},\,\overrightarrow{AC}\] không đồng phẳng
[C]. Các vec tơ \[\overrightarrow{AN},\,\,\overrightarrow{CM},\,\overrightarrow{MN}\] đồng phẳng
[D]. Các vec tơ \[\overrightarrow{AC},\,\,\overrightarrow{BD},\,\overrightarrow{MN}\] đồng phẳng
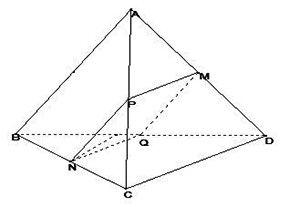
Gọi P, Q lần lượt là trung điểm AC, BD
\[\Rightarrow \] Ba vec tơ \[\underrightarrow{\overrightarrow{AB}},\overrightarrow{DC},\overrightarrow{MN}\] có giá song song hoặc nằm trên mặt phẳng (MNPQ) nên 3 véc tơ này đồng phẳng \[\Rightarrow \] A đúng
Ba vec tơ \[\overrightarrow{\underrightarrow{AB}},\overrightarrow{AC},\overrightarrow{MN}\]không đồng phẳng \[\Rightarrow \] B đúng
Ba vec tơ \[\overrightarrow{\underrightarrow{AN}},\overrightarrow{CM},\overrightarrow{MN}\] có giá không thể song song với mặt phẳng nào \[\Rightarrow \] C sai
Chọn C
Câu 20
Cho hình lập phương \[ABCD.{{A}^{‘}}{{B}^{‘}}{{C}^{‘}}{{D}^{‘}}\], có cạnh a. Hãy tìm mệnh đề sai trong các mệnh đề sau:
[A].\[\overrightarrow{AD’}.\overrightarrow{CC’}=-{{a}^{2}}\]
[B].\[\overrightarrow{AD’}.\overrightarrow{AB’}={{a}^{2}}\]
[C]. \[\overrightarrow{AB’}.\overrightarrow{CD’}=0\]
[D].\[\left| \overrightarrow{AC} \right|=a\sqrt{3}\]
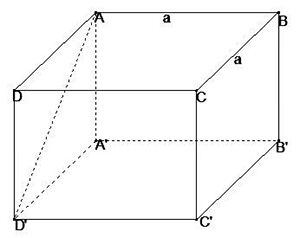
Xết phương án A có: \[\overrightarrow{AD’}.\overrightarrow{CC’}=\overrightarrow{AD’}.\overrightarrow{\text{AA}’}=\left| \overrightarrow{AD’} \right|.\left| \overrightarrow{\text{AA}’} \right|\text{cos4}{{\text{5}}^{0}}={{a}^{2}}\]
Chọn A
Câu 21
Trong không gian cho hai tia Ax, By chéo nhau sao cho AB vuông góc với cả hai tia đó. Các điểm M, N lần lượt thay đổi trên Ax, By sao cho độ dài đoạn MN luôn bằng giá trị c không đổi (c\[\ge \] AB). Gọi \[\varphi \] là góc giữa Ax, By. Giá trị lơn nhất của AM, BN
[A].\[\dfrac{{{c}^{2}}-A{{B}^{2}}}{2(1-c\text{os}\varphi \text{)}}\]
[B]. \[\dfrac{{{c}^{2}}-A{{B}^{2}}}{2(1+c\text{os}\varphi \text{)}}\]
[C]. \[\dfrac{{{c}^{2}}+A{{B}^{2}}}{2(1-c\text{os}\varphi \text{)}}\]
[D]. \[\dfrac{{{c}^{2}}+A{{B}^{2}}}{2(1+c\text{os}\varphi \text{)}}\]
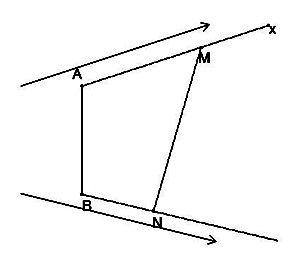
Ta có: \[{{c}^{2}}=M{{N}^{2}}={{\overrightarrow{MN}}^{2}}={{(\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN})}^{2}}\]
\[\ge A{{B}^{2}}+2AM.BN.(1-co\text{s}\varphi \text{)}\] \[\Rightarrow AM.BN.\le \dfrac{{{c}^{2}}-A{{B}^{2}}}{2(1-c\text{os}\varphi )}\]
Vậy biểu thức AM.BN đạt giá trị lớn nhất bằng \[\dfrac{{{c}^{2}}-A{{B}^{2}}}{2(1-c\text{os}\varphi )}\]
Chọn A