Đường thẳng song song với mặt phẳng, trắc nghiệm toán 11
Câu 1
Cho hai đường thẳng $a$ và $b$ chéo nhau. Mệnh đề nào sau đây đúng?
[A]. Tồn tại hai đường thẳng \[c\], \[d\] song song với nhau, mỗi đường đều cắt cả \[a\] và \[b\].
[B]. Không thể tồn tại hai đường thẳng \[c\], \[d\] phân biệt mỗi đường đều cắt cả \[a\] và \[b\].
[C]. Không thể tồn tại một đường thẳng cắt cả \[a\] và \[b\].
[D]. Cả ba câu trên đều sai.
- Đáp án D.
Đáp án A sai. Giả sử \[c\] cắt \[a,b\] lần lượt tại \[A,B\], \[d\] cắt \[a,b\] lần lượt tại \[C,D\]. Suy ra \[A,B,C,D\] đồng phẳng, hay \[a,b\] đồng phẳng, vô lí.
Đáp án B, C sai, chúng ta có thể dễ dàng thấy một ví dụ là tứ diện \[ABCD\] có \[AB\] và \[CD\] đếu cắt hai đường thẳng chéo nhau \[AD\] và \[BC\].
Câu 2
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy
[A]. Đôi một cắt nhau.
[B]. Đồng quy.
[C]. Hoặc đồng quy hoặc đôi một song song.
[D]. Đôi một song song.
- Đáp án C.
Câu 3
Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ:
[A]. Song song với hai đường thẳng đó.
[B]. Song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
[C]. Trùng với một trong hai đường thẳng đó.
[D]. Cắt một trong hai đường thẳng đó.
- Đáp án B.
Câu 4
Cho hai đường thẳng \[a\] và \[b\] chéo nhau. Xét hai đường thẳng \[p\], \[q\] mà mỗi đường thẳng đều cắt cả \[a\] và \[b\], \[p\] cắt \[a\] tại \[M\], \[q\] cắt \[a\] tại \[N\] (\[M\] không trùng với \[N\]). Khi đó hai đường thẳng \[p\] và \[q\]:
[A]. Cắt nhau.
[B]. Trùng nhau.
[C]. Song song với nhau.
[D]. Hoặc chéo nhau hoặc cắt nhau.
- Đáp án D.
Câu 5
Hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó:
[A]. Song song.
[B]. Trùng nhau.
[C]. Chéo nhau.
[D]. Hoặc song song hoặc trùng nhau.
- Đáp án D.
Câu 6
Giả sử \[\left( P \right)\], \[\left( Q \right)\], \[\left( R \right)\] là ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt \[a\], \[b\], \[c\]. Trong đó: \[a=\left( P \right)\cap \left( R \right)\], \[b=\left( Q \right)\cap \left( R \right)\], \[c=\left( P \right)\cap \left( Q \right)\].
Trong các mệnh đề sau, mệnh đề nào sai?
[A]. \[a\] và \[b\] cắt nhau hoặc song song với nhau.
[B]. Ba giao tuyến \[a\], \[b\], \[c\] đồng quy hoặc đôi một cắt nhau.
[C]. Nếu \[a\] và \[b\] song song với nhau thì \[a\] và \[c\] không thể cắt nhau, cũng vậy, \[b\] và \[c\] không thể cắt nhau.
[D]. Ba giao tuyến \[a\], \[b\], \[c\] đồng quy hoặc đôi một song song.
- Đáp án B.
Câu 7
Cho hình chóp \[SABCD\] có đáy là hình bình hành. Khi đó giao tuyến của hai mặt phẳng \[\left( SBC \right)\] và \[\left( SAD \right)\] là đường thẳng \[d\]:
[A]. Đi qua \[S\] .
[B]. Đi qua điểm \[S\] và song song với \[AB\].
[C]. Đi qua điểm \[S\] và song song với \[AD\].
[D]. Đi qua điểm \[S\] và song song với \[AC\].
- Đáp án C.
Câu 8
Giả sử có ba đường thẳng \[a\], \[b\], \[c\] trong đó \[b//a\] và \[c//a\]. Hãy chọn câu đúng:
[A]. Nếu mặt phẳng \[\left( a,b \right)\] không trùng với mặt phẳng \[\left( a,c \right)\] thì \[b\] và \[c\] chéo nhau.
[B]. Nếu mặt phẳng \[\left( a,b \right)\] trùng với mặt phẳng \[\left( a,c \right)\] thì ba đường thẳng \[a\], \[b\], \[c\] song song với nhau từng đôi một.
[C]. Dù cho hai mặt phẳng \[\left( a,b \right)\] và \[\left( a,c \right)\] có trùng nhau hay không, ta vẫn có \[b//c\].
[D]. Cả ba câu trên đều sai.
- Đáp án D.
Đáp án A sai vì nếu \[\left( a,b \right)\] và \[\left( a,c \right)\] không trùng nhau thì \[a,b,c\] đôi một phân biệt. theo tính chất bắc cầu suy ra \[b\parallel c\].
Đáp án B, C sai, vì ta có thể lấy ví dụ \[b\equiv c\].
Câu 9
Cho hai đường thẳng \[a\], \[b\]. Hai đường thẳng này sẽ nằm ở một trong các trường hợp:
- Hai đường thẳng phân biệt trong không gian.
- Hai đường thẳng phân biệt trong mặt phẳng.
- \[a\] là giao tuyến của \[\left( P \right)\] và \[\left( R \right)\], \[b\] là giao tuyến của \[\left( Q \right)\] và \[\left( R \right)\], trong đó \[\left( P \right)\], \[\left( Q \right)\], \[\left( R \right)\] là ba mặt phẳng khác nhau từng đôi một.
Tương ứng với mỗi trường hợp trên, số các khả năng có thể xảy ra giữa \[a\] và \[b\] lần lượt là:
[A]. 3, 2, 2.
[B]. 3, 2, 3.
[C]. 2, 3, 2.
[D]. 3, 2, 1.
- Đáp án B.
Trường hợp \[\left( 1 \right)\] có thể xảy ra giữa hai đường thẳng \[a,b\]là chéo nhau, song song, cắt nhau.
Trường hợp \[\left( 2 \right)\] có thể là song song, cắt nhau.
Trường hợp \[\left( 3 \right)\] có thể là song song, cắt nhau hoặc trùng nhau.
Như vậy, tương ứng với mối trường hợp, số các khả năng có thể xảy ra giữa \[a,b\] là \[3,2,3\].
Câu 10
Xét hình bên dưới:
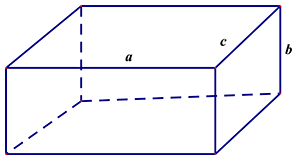
Các cạnh của hình hộp nằm trên các đường thẳng \[a\], \[b\], \[c\] như hình vẽ:
- Đường thẳng \[a\] và đường thẳng \[b\] cùng nằm trên một mặt phẳng.
- Có một mặt phẳng qua hai đường thẳng \[a\] và \[c\].
- Có một mặt phẳng qua hai đường thẳng \[b\] và \[c\].
Trong ba câu trên:
[A]. Chỉ có (1) và (2) đúng.
[B]. Chỉ có (1) và (3) đúng.
[C]. Chỉ có (2) và (3) đúng.
[D]. Cả ba câu trên đều đúng.
- Đáp án C.
Nhìn vào hình vẽ, ta thấy \[a,b\] chéo nhau, nên không có mặt phẳng nào chứa cả \[a,b\]. Do đó \[\left( 1 \right)\] sai. Vậy đáp án A, B, C sai.
Đường thẳng \[a,c\] cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án \[\left( 2 \right)\] đúng.
Đường thẳng \[b,c\] cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án \[\left( 3 \right)\] đúng.
Câu 11
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang đáy lớn là \[CD\]. Gọi M là trung điểm của \[SA\], \[N\] là giao điểm của cạnh \[SB\] và mặt phẳng \[\left( MCD \right)\]. Mệnh đề nào sau đây đúng?
[A]. \[MN\] và \[SD\] cắt nhau.
[B]. \[MN\] và \[CD\] chéo nhau.
[C]. \[MN\] và \[SC\] cắt nhau.
[D]. \[MN\] và \[CD\] song song với nhau.
- Đáp án D.
Ta có: \[\left\{ \begin{align}
& AB\parallel CD \\
& AB\subset \left( SAB \right),CD\subset \left( MCD \right) \\
& MN=\left( SAB \right)\cap \left( MCD \right) \\
\end{align} \right.\Rightarrow MN\parallel CD\].
Câu 12
Cho tứ diện \[ABCD\]. Gọi \[M,N,P,Q\] lần lượt là trung điểm của các cạnh \[AB,AD,CD,BC\]. Mệnh đề nào sau đây sai?
[A]. \[MP,NQ\] chéo nhau.
[B]. \[MN\parallel PQ\] và \[MN=PQ\].
[C]. \[MNPQ\] là hình bình hành.
[D]. \[MN\parallel BD\] và \[MN=\dfrac{1}{2}BD\].
- Đáp án A.
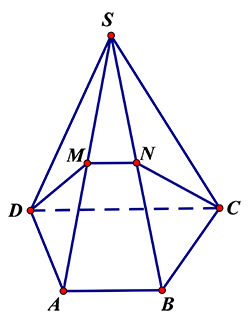
Do \[M,N\] lần lượt là trung điểm của \[AB,AD\] nên \[MN\parallel BD,MN=\dfrac{1}{2}BD\].
Do \[P,Q\] lần lượt là trung điểm của \[CD,CB\] nên \[PQ\parallel BD,PQ=\dfrac{1}{2}BD\].
Suy ra \[MN\parallel PQ\], do đó \[M,N,P,Q\] đồng phẳng. Do đó \[MP,NQ\] không thể chéo nhau.
Câu 13
Cho hình chóp \[S.ABCD\] với đáy \[ABCD\] là hình bình hành. Gọi \[M,N,P,Q\] lần lượt là trung điểm của các cạnh \[SA,SB,SC,SD\]. Đường thẳng nào sau đây không song song với đường thẳng \[MN\]?
[A]. \[AB\].
[B]. \[CD\].
[C]. \[PQ\].
[D]. \[SC\].
- Đáp án D.
Do \[MN\] là đường trung bình của tam giác \[SAB\] nên \[MN\parallel AB\].
Tương tự, do \[PQ\] là đường trung bình của tam giác \[SCD\] nên \[PQ\parallel CD\].
\[ABCD\] là hình bình hành nên \[AB\parallel CD\]. Do đó: \[PQ\parallel MN\] và \[MN\parallel CD\].
\[MN\] không song song với \[SC\] vì giả sử ngược lại thì \[SC\] và \[CD\] trùng nhau (vô lí).
Câu 14
Cho hình chóp \[A.BCD\] với đáy \[ABCD\] là hình bình hành. Gọi \[M,N,P,Q,R,S\] lần lượt là trung điểm của các cạnh \[AC,BD,AB,CD,AD,BC\]. Các điểm nào sau đây không đồng phẳng?
[A]. \[M,P,R,Q\].
[B]. \[M,R,S,N\].
[C]. \[P,Q,R,S\].
[D]. \[M,P,Q,N\].
- Đáp án A.
Do \[M,N,P,Q,R,S\] lần lượt là trung điểm của \[AC,BD,AB,CD,AD,BC\] nên \[MR\parallel CD\parallel SN\], \[PS\parallel AC\parallel RQ\], \[MP\parallel BC\parallel NQ\]. Do đó \[M,R,S,N\] đồng phẳng; \[P,Q,R,S\] đồng phẳng; \[M,P,Q,N\] đồng phẳng.
\[M,P,R,Q\] không đồng phẳng vì giả sử ngược lại thì \[P\] sẽ thuộc mặt phẳng \[\left( ACD \right)\], suy ra \[B\] thuộc mặt phẳng \[\left( ACD \right)\] (vô lí).
Câu 15
Cho hình chóp \[S.ABCD\] với đáy \[ABCD\] là hình thang với đáy \[AD\] và \[BC\] \[\left( AD=a>BC=b \right)\]. Gọi \[I,J\] lần lượt là trọng tâm các tam giác \[SAD\] và \[SBC\]. Mặt phẳng \[\left( ADJ \right)\] cắt \[SB,SC\] lần lượt tại \[M,N\]. Mặt phẳng \[\left( BCI \right)\] cắt \[SA,SD\] lần lượt tại \[P,Q\]. Gọi \[E\] là giao điểm của \[AM\] và \[PB\], \[F\] là giao điểm của \[CQ\] và \[DN\]. Trong các mệnh đề dưới đây, có bao nhiêu mệnh đề sai?
- \[MN\] và \[PQ\] song song với nhau.
- \[MN\] và \[EF\] song song với nhau.
- \[EF=\dfrac{2}{5}\left( a+b \right)\].
- \[EF=\dfrac{1}{4}\left( a+b \right)\]
[A]. \[4\].
[B]. \[1\].
[C]. \[2\].
[D]. \[3\].
- Đáp án B.
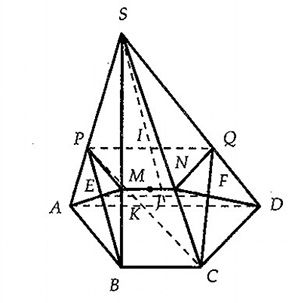
Ta có \[I\in \left( SAD \right)\], suy ra \[I\in \left( SAD \right)\cap \left( BCI \right)\].
Do \[\left\{ \begin{align}
& \left( SAD \right)\cap \left( BCI \right)=PQ \\
& AD\subset \left( SAD \right),BC\subset \left( BCI \right) \\
& AD\parallel BC \\
\end{align} \right.\]\[\Rightarrow PQ\parallel AD\parallel BC\].
Ta có: \[J\in \left( SBC \right)\], suy ra \[J\in \left( SBC \right)\cap \left( ADJ \right)\].
Do \[\left\{ \begin{align}
& \left( SBC \right)\cap \left( ADJ \right)=MN \\
& BC\subset \left( SBC \right),AD\subset \left( ADJ \right) \\
& AD\parallel BC \\
\end{align} \right.\]\[\Rightarrow MN\parallel AD\parallel BC\].
Từ đó suy ra \[MN\] và \[PQ\] song song với nhau.
Ta có: \[\left\{ \begin{align}
& EF=\left( ADNM \right)\cap \left( BCQP \right) \\
& AD=\left( ADNM \right)\cap \left( ABCD \right) \\
& BC=\left( ABCD \right)\cap \left( BCQP \right) \\
& AD\parallel BC \\
\end{align} \right.\]\[\Rightarrow EF\parallel AD\].
Suy ra \[EF\parallel MN\]. Gọi \[K\] là giao điểm của \[CP\] với \[EF\]\[EF=EK+KF\].
Do \[\dfrac{SP}{SA}=\dfrac{2}{3}=\dfrac{SM}{SB}\Rightarrow PM\parallel AB\].
Theo định lý Thalet ta có: \[\dfrac{PE}{EB}=\dfrac{2}{3}\Rightarrow \dfrac{PE}{PB}=\dfrac{2}{5}\]. Do \[EK\] song song với \[BC\] nên theo định lý Thalet ta có : \[\dfrac{PE}{PB}=\dfrac{EK}{BC}=\dfrac{2}{5}\Rightarrow EK=\dfrac{2}{5}b\].
Tương tự ta cũng có: \[\dfrac{QF}{FC}=\dfrac{2}{3}\Rightarrow \dfrac{QC}{FC}=\dfrac{5}{3}\Rightarrow \dfrac{PQ}{FK}=\dfrac{5}{3}\Rightarrow FK=\dfrac{3}{5}PQ=\dfrac{3}{5}.\dfrac{2}{3}AD=\dfrac{2}{5}a\].
Từ đây suy ra \[EF=\dfrac{2}{5}\left( a+b \right)\].
Câu 16
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AC,BC\]. \[K\] là điểm trên đoạn \[BD\] sao cho \[KB=2KD\], \[F\] là giao điểm của \[AD\] và \[\left( IJK \right)\]. Giao tuyến của hai mặt phẳng \[\left( SAD \right)\] và \[\left( IJK \right)\] song song với đường thẳng?
[A]. \[AJ\].
[B]. \[BI\].
[C]. \[IJ\].
[D]. \[CI\].
- Đáp án C.
Ta có: \[\left\{ \begin{align}
& \left( SAD \right)\cap \left( IJK \right)=FK \\
& AD\subset \left( SAD \right),IJ\subset \left( IJK \right) \\
& AD\parallel IJ \\
\end{align} \right.\]\[\Rightarrow FK\parallel IJ\].
Dễ dàng chứng minh được các đường thẳng còn lại không song song với \[FK\].
Câu 17
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[BC,BD\]. Giao tuyến của hai mặt phẳng \[\left( AIJ \right)\] và \[\left( ACD \right)\] là:
[A]. Đường thẳng \[d\] đi qua \[A\] và \[d\parallel BC\].
[B]. Đường thẳng \[d\] đi qua \[A\] và \[d\parallel BD\].
[C]. Đường thẳng \[d\] đi qua \[A\] và \[d\parallel CD\].
[D]. Đường thẳng \[AB\].
- Đáp án C.
Do \[I,J\] lần lượt là trung điểm của \[BC,BD\] nên \[IJ\] là đường trung bình của tam giác \[BCD\]. Suy ra \[IJ\parallel CD\].
Ta có: \[\left\{ \begin{align}
& IJ\parallel CD,IJ\subset \left( AIJ \right),CD\subset \left( ACD \right) \\
& A\in \left( AIJ \right)\cap \left( ACD \right) \\
\end{align} \right.\]\[\Rightarrow \left( AIJ \right)\cap \left( ACD \right)=At\parallel CD\].
Câu 18
Cho hình chóp \[S.ABC\], \[M\] là một điểm nằm trong tam giác \[ABC\]. Các đường thẳng qua \[M\] song song với \[SA,SB,SC\] cắt các mặt phẳng \[\left( SBC \right),\left( SAC \right),\left( SAB \right)\] lần lượt tại \[{A}’,{B}’,{C}’\].
a/ \[\dfrac{M{A}’}{SA}+\dfrac{M{B}’}{SB}+\dfrac{M{C}’}{SC}\] có giá trị không đổi bằng bao nhiêu khi \[M\] di động trong tam giác \[ABC\]?
[A]. \[\dfrac{1}{3}\].
[B]. \[\dfrac{1}{2}\].
[C]. \[1\].
[D]. \[\dfrac{2}{3}\].
b/ \[\dfrac{M{A}’}{SA}.\dfrac{M{B}’}{SB}.\dfrac{M{C}’}{SC}\] nhận giá trị lớn nhất. Khi đó vị trí của \[M\] trong tam giác \[ABC\] là:
[A]. Trực tâm \[\Delta ABC\].
[B]. Trọng tâm \[\Delta ABC\].
[C]. Tâm ngoại tiếp \[\Delta ABC\].
[D]. Tâm nội tiếp \[\Delta ABC\].
- Đáp án C, B.
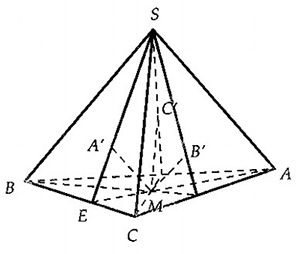
a) Do \[M{A}’\parallel SA\] nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử \[E\] là giao điểm của mặt phẳng này với \[BC\]. Khi đó \[A,M,E\] thẳng hàng và ta có: \[\dfrac{M{A}’}{SA}=\dfrac{ME}{EA}=\dfrac{{{S}_{MBC}}}{{{S}_{ABC}}}\].
Tương tự ta có: \[\dfrac{M{B}’}{SB}=\dfrac{{{S}_{MAC}}}{{{S}_{ABC}}},\dfrac{M{C}’}{SC}=\dfrac{{{S}_{MAB}}}{{{S}_{ABC}}}\]. Vậy \[\dfrac{M{A}’}{SA}+\dfrac{M{B}’}{SB}+\dfrac{M{C}’}{SC}=1\]. Vậy đáp án đúng là .
b) Ap dụng bất đẳng thức Cauchy ta có :
\[\dfrac{M{A}’}{SA}+\dfrac{M{B}’}{SB}+\dfrac{M{C}’}{SC}\ge 3\sqrt[3]{\dfrac{M{A}’}{SA}.\dfrac{M{B}’}{SB}.\dfrac{M{C}’}{SC}}\Rightarrow \dfrac{M{A}’}{SA}.\dfrac{M{B}’}{SB}.\dfrac{M{C}’}{SC}\le \dfrac{1}{27}\].
Dầu bằng xảy ra khi và chỉ khi: \[\dfrac{M{A}’}{SA}=\dfrac{M{B}’}{SB}=\dfrac{M{C}’}{SC}\Rightarrow {{S}_{MAC}}={{S}_{MAB}}={{S}_{MBC}}\].
Điều này chỉ xảy ra khi \[M\] là trọng tâm tam giác \[ABC\]. Vậy đáp án đúng là B.
Câu 19
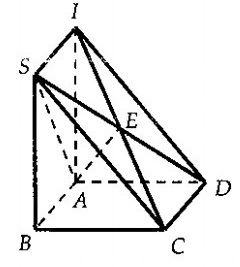
Cho hình chóp \[S.ABCD\] với đáy \[ABCD\] là hình bình hành tâm \[O\]. Mặt phẳng \[\left( \alpha \right)\] di động đi qua \[AB\] và cắt \[SC,SD\] lần lượt tại \[M,N\].
a/ Tứ giác \[ABMN\] là hình gì?
[A]. Hình bình hành.
[B]. Hình thang.
[C]. Hình thoi.
[D]. Tứ giác lồi có các cặp cạnh đối cắt nhau.
b/ Giao điểm của hai đường thẳng \[AM\] và \[BN\] luôn chạy trên đường thẳng cố định:
A.\[SO\].
[B]. Đường thẳng đi qua \[S\].
[C]. Đường thẳng đi qua \[S\], song song với \[AB\].
[D]. Đường thẳng đi qua \[S\], song song với \[AD\].
c/ Giao điểm của hai đường thẳng \[AN\] và \[BM\] luôn chạy trên đường thẳng cố định:
A.\[SO\].
[B]. Đường thẳng đi qua \[S\].
[C]. Đường thẳng đi qua \[S\], song song với \[AB\].
[D]. Đường thẳng đi qua \[S\], song song với \[AD\].
d/ Tính \[\dfrac{AB}{MN}-\dfrac{BC}{SK}\]?
[A]. \[0\].
[B]. \[\dfrac{1}{2}\].
[C]. \[\dfrac{1}{3}\].
[D]. \[\dfrac{2}{3}\].
- Đáp án B, A, D, A.
a) Ta có : \[\left\{ \begin{align}
& MN=\left( ABM \right)\cap \left( SCD \right) \\
& AB=\left( ABM \right)\cap \left( ABCD \right) \\
& CD=\left( ABCD \right)\cap \left( SCD \right) \\
& CD\parallel AB \\
\end{align} \right.\]\[\Rightarrow MN\parallel AB\].
Do đó \[ABMN\] là hình thang. Do \[MN<AB\] nên \[ABMN\] không thể là hình bình hành, hinh thoi. Vậy đáp án đúng là B.
b) Gọi \[I=AM\cap BN\Rightarrow \left\{ \begin{align}
& I\in \left( SAC \right) \\
& I\in \left( SBD \right) \\
\end{align} \right.\]\[\Rightarrow I\in SO=\left( SAC \right)\cap \left( SBD \right)\]. Vậy đáp án đúng là A.
c) Gọi \[K=AN\cap BM\Rightarrow \left\{ \begin{align}
& I\in \left( SAD \right) \\
& I\in \left( SBC \right) \\
\end{align} \right.\]\[\Rightarrow I\in \left( SAD \right)\cap \left( SBC \right)\].
Giao tuyến của hai mặt phẳng \[\left( SAD \right)\] và \[\left( SBC \right)\] là đường thẳng qua \[S\] và song song với \[AD\].
Vậy đáp án đúng là D.
d) Do \[MN\parallel AB\] nên \[\dfrac{AB}{MN}=\dfrac{BM}{MK}\text{ }\left( 1 \right)\].
Do \[SK\parallel BC\] nên \[\dfrac{CB}{SK}=\dfrac{MB}{MK}\text{ }\left( 2 \right)\].
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[\dfrac{AB}{MN}-\dfrac{BC}{SK}=0\]. Vậy đáp án đúng là A.
Câu 20
Cho tứ diện \[ABCD\]. Gọi \[G\] là trọng tâm tam giác \[BCD\] và \[M\] là điểm nằm bên trong tam giác \[BCD\]. Đường thẳng qua \[M\] và song song với \[GA\] lần lượt cắt các mặt phẳng \[\left( ABC \right),\left( ACD \right),\left( ADB \right)\] tại \[P,Q,R\].
a/ Khi \[M\] di động trong tam giác \[BCD\], đại lượng \[\dfrac{MP+MQ+MR}{GA}\] không đổi và bằng:
[A]. \[1\].
[B]. \[2\].
[C]. \[3\].
[D]. \[4\].
b/ Xác định vị trí của \[M\] để \[MP.MQ.MR\] đạt giá trị lớn nhất?
[A]. \[M\] là trực tâm tam giác \[BCD\].
[B]. \[M\] là tâm ngoại tiếp tam giác \[BCD\].
[C]. \[M\] là trọng tâm tam giác \[BCD\].
[D]. \[M\] là tâm ngoại tiếp tam giác \[BCD\].
- Đáp án C, C.
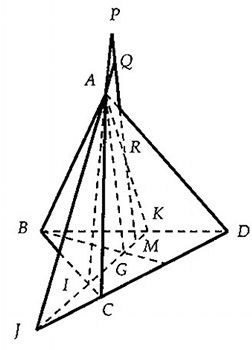
a) Trong mặt phẳng \[\left( BCD \right)\], gọi \[I=MG\cap BC,J=MG\cap CD,K=MG\cap BD\].
Qua \[M\] kẻ \[Mx\parallel GA\]. Trong \[\left( AIJ \right):Mx\cap AI=P\](đây chính là giao điểm của \[Mx\] với \[\left( ABC \right)\])
Tương tự \[Mx\cap AK=R,Mx\cap AJ=Q\].
Ta có : \[\dfrac{IM}{IG}=\dfrac{{{S}_{MIC}}}{{{S}_{GIC}}}=\dfrac{{{S}_{MIB}}}{{{S}_{GIB}}}=\dfrac{{{S}_{MIC}}+{{S}_{MIB}}}{{{S}_{GIC}}+{{S}_{GIB}}}=\dfrac{{{S}_{MBC}}}{{{S}_{GBC}}}=\dfrac{3{{S}_{MBC}}}{{{S}_{BCD}}}\].
Theo định lý Thalet ta có : \[\dfrac{IM}{IG}=\dfrac{MP}{GA}\]. Do đó : \[\dfrac{MP}{GA}=\dfrac{3{{S}_{MBC}}}{{{S}_{BCD}}}\].
Chứng minh tương tự ta có : \[\dfrac{MQ}{GA}=\dfrac{3{{S}_{MCD}}}{{{S}_{BCD}}},\dfrac{MR}{GA}=\dfrac{3{{S}_{MBD}}}{{{S}_{BCD}}}\Rightarrow \dfrac{MP+MQ+MR}{GA}=3\].
Vậy đáp án đúng là C.
b) Áp dụng bất đẳng thức Cauchy ta có : \[MP.MQ.MR\le {{\left( \dfrac{MP+MQ+MR}{3} \right)}^{3}}=G{{A}^{3}}\].
Vậy giá trị lớn nhất của \[MP.MQ.MR\] bằng \[G{{A}^{3}}\]. Dấu bằng xảy ra khi và chỉ khi \[MP=MQ=MR\]. Điều này xảy ra khi \[M\] là trọng tâm tam giác \[BCD\]. Vậy đáp án đúng là C.
Câu 21
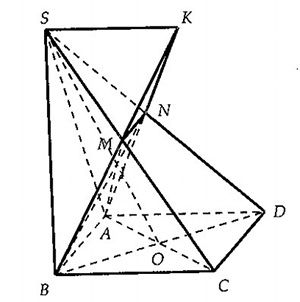
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], tâm \[O\]. Mặt bên \[\left( SAB \right)\] là tam giác đều và \[\widehat{SAD}=90{}^\circ \]. Gọi \[Dx\] là đường thẳng qua \[D\] và song song với \[SC\].
a/ Giao điểm \[I\] của đường thẳng \[Dx\] với mặt phẳng \[\left( SAB \right)\] chạy trên đường thẳng:
[A]. Qua \[S\] và song song với \[AB\].
[B]. Qua \[S\] và song song với \[AD\]
[C]. \[SO\].
[D]. \[SD\].
b/ Diện tích thiết diện của hình chóp \[S.ABCD\] cắt bởi \[\left( AIC \right)\] là:
[A]. \[\dfrac{{{a}^{2}}\sqrt{7}}{8}\].
[B]. \[\dfrac{{{a}^{2}}\sqrt{7}}{4}\].
[C]. \[\dfrac{{{a}^{2}}\sqrt{7}}{2}\].
[D]. \[\dfrac{{{a}^{2}}\sqrt{7}}{16}\].
- Đáp án A, A.
a) Do \[Dx\parallel SC\] nên hai đường thẳng này cùng nằm trong mặt phẳng \[\left( SCD \right)\].
Lại có, hai mặt phẳng \[\left( SAB \right)\] và \[\left( SCD \right)\] có \[D\] là điểm chung, \[AB\parallel CD\] nên giao tuyến là đường thẳng đi qua \[S\] và song song với \[AB\]. Vậy \[I\] thuộc giao tuyến này.
Vậy đáp án đúng là A.
b) Gọi \[E\] là giao điểm của \[SD\] và \[IC\]. Suy ra thiết diện của hình chóp cắt bởi mặt phẳng \[\left( AIC \right)\] là tam giác \[ACE\].
Ta có \[SIDC\] là hình thang nên \[SI=CD\] và \[SI\parallel CD\]. Suy ra \[SI=AB\] và \[SI\parallel AB\]. Điều này suy ra \[SIDC\] là hình bình hành. Khi đó \[AI=SB=a\].
Mặt khác, \[AC=SD=a\sqrt{2}\Rightarrow AE=\dfrac{a\sqrt{2}}{2}\].
Xét tam giác \[IAC\] có : \[C{{I}^{2}}=2\left( A{{C}^{2}}+A{{I}^{2}} \right)-4A{{E}^{2}}=4{{a}^{2}}\Rightarrow CI=2a\].
Ta có : \[\cos \widehat{CAE}=\dfrac{A{{E}^{2}}+A{{C}^{2}}-C{{E}^{2}}}{2AC.AE}=\dfrac{\dfrac{{{a}^{2}}}{2}+2{{a}^{2}}-{{a}^{2}}}{2{{a}^{2}}}=\dfrac{3}{4}\Rightarrow \sin \widehat{CAE}=\dfrac{\sqrt{7}}{4}\].
Diện tích thiết diện là : \[S=\dfrac{1}{2}AC.AE.\sin \widehat{CAE}=\dfrac{1}{2}a\sqrt{2}.\dfrac{a\sqrt{2}}{2}.\dfrac{\sqrt{7}}{4}=\dfrac{{{a}^{2}}\sqrt{7}}{8}\].
Vậy đáp án đúng là A.