Đại cương về đường thẳng và mặt phẳng, trắc nghiệm toán 11
Câu 1
Trong các mệnh đề sau mệnh đề nào sai?
[A]. Dùng nét đứt biểu diễn cho đường bị che khuất.
[B]. Hình biểu diễn của đường thẳng là đường thẳng.
[C]. Hình biểu diễn phải giữ nguyên qua hệ thuộc giữa điểm và đường thẳng..
[D]. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song.
Đáp án D.
Câu 2
Trong các hình vẽ sau hình nào có thể là hình biểu diễn của một hình tứ diện? (Chọn câu đúng nhất)
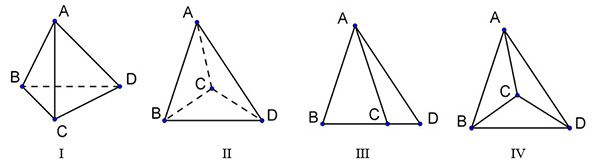
[A]. $\left( I \right),\left( II \right).$ .
[B]. $\left( I \right),\left( II \right),\left( III \right),\left( IV \right)$ .
[C]. $\left( I \right),\left( II \right),\left( III \right)$.
[D]. $\left( I \right).$
Đáp án B.
Câu 3
Hình nào sau đây vẽ đúng quy tắc?
[A]. 
[B]. 
[C]. 
[D]. 
Đáp án A.
Câu 4
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$ gấp đôi đáy nhỏ $CD$ , $E$ là trung điểm của đoạn $AB$ . Hình vẽ nào sau đây vẽ đúng quy tắc?
[A]. 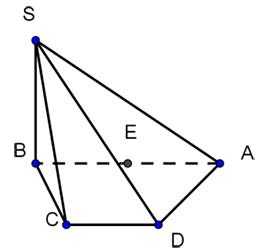
[B]. 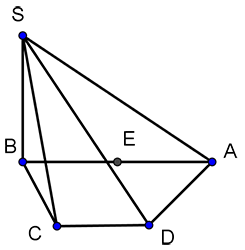
[C]. 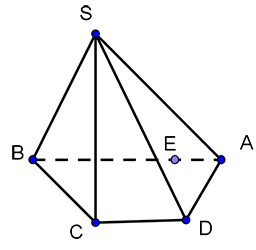
[D]. 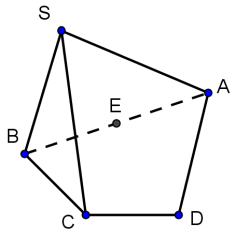
Đáp án A.
Theo quy tắc vẽ hình, các đoạn thẳng song song được vẽ bằng các đoạn thẳng song song nên đáp án D bị loại. Trung điểm được vẽ ở chính giữa đoạn nên ý C bị loại. Nét khuất được vẽ bởi nét đứt đoạn, nét với góc nhìn này với đáp án B thì hoặc AB đứt đoạn hoặc SC, SD đứt đoạn. Do đó chỉ có đáp án A đúng.
Câu 5
Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên)), hình chiếu cạnh (từ trái sang (có thể nhìn từ phải sang)) lần lượt được thể hiện như sau:
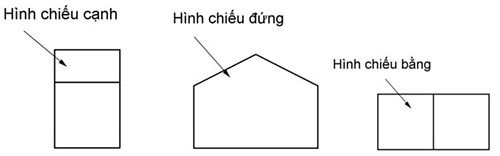
Hãy vẽ hình biểu diễn của hình đó?
[A]. 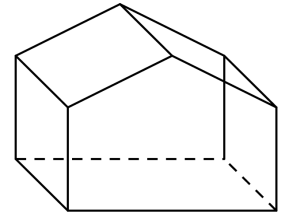
[B]. 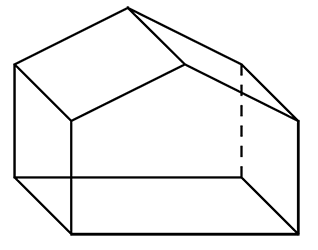
[C]. 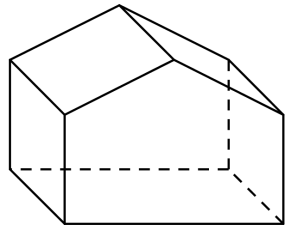
[D]. 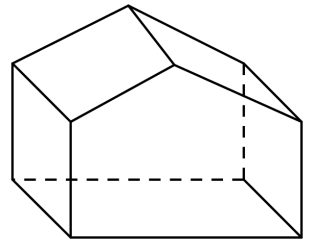
Đáp án C.
Hình A, B, D sai khi vẽ các đường không nhìn thấy bằng nét liền.
Câu 6
Mệnh đề nào sau đây đúng?
[A]. Qua ba điểm xác định một và chỉ một mặt phẳng.
[B]. Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.
[C]. Qua ba điểm phân biệt không thẳng hàng xác định hai mặt phẳng phân biệt.
[D]. Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.
Đáp án D.
– Đáp án A, B sai, các em có thể lấy ví dụ ba điểm $A,B,C$phân biệt , thẳng hàng , thì có vô số mặt phẳng đi qua ba điểm đó.
– Đáp án C sai, vì theo tính chất thừa nhận, ba điểm phân biệt không thẳng hàng có duy nhất một mp đi qua ba điểm.
Câu 7
Xét các mệnh đề sau đây:
$\left( I \right)$ Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
$\left( II \right)$ Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
$\left( III \right)$ Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
$\left( IV \right)$ Nếu hai mặt phẳng có một điểm chung thì chúng còn có duy nhất một điểm chung khác nữa.
Số mệnh đề sai trong các mệnh đề trên là:
[A]. 3.
[B]. 1.
[C]. 2.
[D]. 4.
Đáp án B.
Theo các tính chất thừa nhận, ta thấy (I), (II), (III) đúng và nếu hai mp có 1 điểm chung thì chúng còn vô số điểm chung khác nữa. Điều đó đồng nghĩa với nhận xét (IV) là sai. Như vậy có 1 quy tắc sai.
Câu 8
Cho $n$ điểm phân biệt trong không gian $\left( n>4 \right)$ .Biết rằng bốn điểm bất kỳ trong $n$ điểm đã cho cùng thuộc một mặt phẳng. Khẳng định nào sau đây đúng?
[A]. Tất cả $n$ điểm thuộc cùng một mặt phẳng.
[B]. Có đúng $n-1$ điểm thuộc cùng một mặt phẳng.
[C]. Có đúng $n-2$ điểm thuộc cùng một mặt phẳng.
[D]. Không tồn tại mặt phẳng nào chứa tất cả $n$ điểm.
Đáp án A.
– Nếu $n$ điểm đã cho cùng thuộc một đường thẳng thì hiển nhiên $n$ điểm thuộc cùng 1 mp. Do đó loại được đáp án B, C, D.
– Nếu $n$ điểm đã cho không cùng thuộc một đường thẳng thì trong chúng phải có 3 điểm không thẳng hàng. Khi đó ba điểm này xác định 1 mp, kí hiệu là mp $\left( P \right)$ . Lấy một điểm trong $n-3$ điểm còn lại thì theo giả thiết điểm đó phải thuộc mp$\left( P \right)$ . Suy ra tất cả các điểm đã cho cùng thuộc 1 mp.
Câu 9
Trong các mệnh đề sau mệnh đề nào đúng?
[A]. Có đúng hai mặt phẳng cắt nhau theo một đường thẳng cho trước..
[B]. Hai mặt phẳng có một điểm chung duy nhất.
[C]. Hai mặt phẳng cùng chứa hai cạnh của một tam giác thì trùng nhau..
[D]. Có đúng hai mặt phẳng phân biệt đi qua ba điểm phân biệt..
Đáp án C.
Một đường thẳng cho trước có vô số mp đi qua.
Hai mp đã có 1 điểm chung thì có vô số điểm chung khác nữa. Còn có trường hợp 2 mp không có điểm chung nào.
Có duy nhất 1 mp đi qua ba điểm phân biệt. Như vậy ta chọn ý C.
Câu 10
Cho tứ giác lồi $ABCD$ và điểm $S$ không thuộc mặt phẳng $\left( ABCD \right)$ . Có bao nhiêu mặt phẳng qua $S$ và hai trong số bốn điểm $A,B,C,D?$
[A]. 3.
[B]. 4.
[C]. 5.
[D]. 6.
Đáp án D.
Số cách chọn 2 trong 4 điểm $A,B,C,D$ là $C_{4}^{2}=6$ .
Vậy có 6 mp đi qua $S$ và 2 trong 4 điểm $A,B,C,D$ .
Câu 11
Cho năm điểm $A,B,C,D,E$ phân biệt trong đó không có bốn điểm nào cùng nằm trên một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm đã cho ?
[A]. 6.
[B]. 10.
[C]. 60.
[D]. 8.
Đáp án B.
Chọn 3 trong 5 điểm trên sẽ tạo nên 1 mp. Do đó, số mp tạo bởi 3 trong 5 điểm trên là \[C_{5}^{3}=10\].
Câu 12
Cho $n\,\,\left( n\ge 3,n\in \mathbb{N} \right)$ đường thẳng phân biệt đồng quy tại O trong đó không có ba đường thẳng nào cùng năm trên một mặt phẳng. Có bao nhiêu mặt phẳng đi qua hai trong số $n$ đường thẳng trên?
[A]. $\dfrac{n!}{2\left( n-2 \right)!}\,$.
[B]. $\,\dfrac{n!}{\left( n-2 \right)!}\,$.
[C]. $\,\dfrac{n!}{2}\,$.
[D]. $\,n!$.
Đáp án A.
Hai đường thẳng phân biệt cắt nhau tại $O$ xác định 1 mp . Nên số các mp chứa 2 trong $n$ đường thẳng trên là \[C_{n}^{2}=\dfrac{n!}{2\left( n-2 \right)!}\] .
Câu 13
Cho mặt phẳng $\left( \alpha \right)$ và hai đường thẳng $a,b$ cắt nhau cùng nằm trong mặt phẳng $\left( \alpha \right)$ . Gọi A là một điểm thuộc đường thẳng $a$ nhưng không thuộc đường thẳng $b$ và $P$ là một điểm nằm ngoài \[\left( \alpha \right)\]. Khẳng định nào sau đây đúng:
[A]. $PA$ và $b$ chéo nhau.
[B]. $PA$ và $b$ song song .
[C]. $PA$ và $b$ cắt nhau.
[D]. $PA$ và $b$ trùng nhau.
Đáp án A .
Dễ thấy $PA,b$ không trùng nhau.
Giả sử $PA,b$ không chéo nhau, khi đó $PA,b$ hoặc song song hoặc cắt nhau. Lúc đó, theo cách xác định 1 mp, ta thấy $PA,b$cùng thuộc 1 mp$\left( \beta \right)$ . Các mp $\left( \alpha \right),\left( \beta \right)$ đều chứa đường thẳng $b$ và đi qua điểm \[A\] ở ngoài $b$ nên 2 mp$\left( \alpha \right),\left( \beta \right)$trùng nhau. Suy ra điểm $P$ phải thuộc mp $\left( \alpha \right)$ (Vô lý). Như vậy $PA,b$ chéo nhau.
Câu 14
Cho tứ diện $ABCD,I,J$ lần lượt là trung điểm của $AD$ và $BC$ . Khẳng định nào sau đây đúng?
[A]. $AJ,BI\,$ song song .
[B]. $AJ,BI\,$ trùng nhau.
[C]. $AJ,BI\,$ cắt nhau
[D]. $AJ,BI\,$chéo nhau
Đáp án D.
Giả sử $AJ,BI$ đồng phẳng, suy ra $AJ,BI$đồng phẳng do đó $A,B,C,D$ cùng thuộc 1 mp (vô lý).
Do đó$AJ,BI$không đồng phẳng, do đó $AJ,BI$ chéo nhau. Chọn đáp án D.
Câu 15
Cho hình chóp $SABCD$ có đáy $ABCD$ là một tứ giác ($AB$ không song song $CD$ ). Gọi $M$ là trung điểm của $SD$ , $N$ là điểm nằm trên cạnh $SB$ sao cho $SN=2NB,O$ là giao điểm của $AC$ và$BD$ . Cặp đường thẳng nào sau đây cắt nhau:
[A]. $SO$ và$AD$.
[B]. $MN$ và $SO$.
[C]. $MN$ và $SC$
[D]. $SA$ và $BC$.
Đáp án B.
Giả sử $SO,AD$ cắt nhau. Khi đó $SO,AD$đồng phẳng, suy ra $S$ thuộc mp $\left( ABCD \right)$ (Vô lý). Đáp án A bị loại.
Giả sử $MN$ cắt $SC$. Khi đó $MN$ và $SC$ đồng phẳng, suy ra $C$ thuộc $\left( SBD \right)$ (vô lý). Do đó đáp án C bị loại.
Giả sử $SA$ cắt $BC$. Khi đó $SA,BC$ đồng phẳng. Suy ra, $S$ thuộc mp $\left( ABCD \right)$ (vô lý). Đáp án D bị loại. $MN,SO$ cùng nằm trong mp$\left( SBD \right)$, không song song và trùng nhau.
Câu 16
Cho bốn điểm $A,B,C,D$ không cùng nằm trong một mặt phẳng. Trên $AB,AD$ lần lượt lấy các điểm $M$ và $N$ sao cho $MN$ cắt $BD$ tại $I$ . Điểm $I$ không thuộc mặt phẳng nào sau đây:
[A]. $\left( ACD \right)$.
[B]. $\left( BCD \right)$.
[C]. $\left( CMN \right)$ .
[D]. $\left( ABD \right)$.
Đáp án A.
Do$I$ là giao điểm của $MN$ và $BD$ nên $I$ thuộc các mp chứa $MN$ và các mp chứa $BD$. Do đó $I$ thuộc $\left( BCD \right),\left( CMN \right),\left( ABD \right).$
Giả sử $I$ thuộc $\left( ACD \right)$ khi đó $B$ thuộc $\left( ACD \right)$ (vô lý).
Câu 17
Cho tứ diện $ABCD$ . Gọi $M,N$ lần lượt là trung điểm của $CD,AB$ . Khi đó $BC$ và $MN$ là hai đường thẳng:
[A]. Chéo nhau.
[B]. Có hai điểm chung.
[C]. Song song
[D]. Cắt nhau
Đáp án A.
Giả sử $MN,BC$ đồng phẳng. Do đó $D,A$ lần lượt thuộc đường thẳng $MC,NB$ nên $D,A$ cũng thuộc mp đó. Như vậy $A,B,C,D$ đồng phẳng(vô lý). Như vậy đáp án B, C, D không thỏa mãn.
Câu 18
Cho tứ diện $ABCD$ . Gọi $M$ là trung điểm cạnh $AC,N$ là điểm thuộc cạnh $AD$ sao cho $AN=2ND.\,O$ là một điểm thuộc miền trong của tam giác $BCD$ . Mệnh đề nào sau đây là mệnh đề đúng?
[A]. Mặt phẳng $\left( OMN \right)$ chứa đường thẳng $AB$
[B]. Mặt phẳng $\left( OMN \right)$ đi qua giao điểm của hai đường thẳng $MN$ và $CD$.
[C]. Mặt phẳng $\left( OMN \right)$ đi qua điểm $A$ .
[D]. Mặt phẳng $\left( OMN \right)$chứa đường thẳng $CD$ .
Đáp án A.
Gọi $I$ là giao điểm của $MN$ và C[D]. Khi đó $I$ thuộc $\left( OMN \right)$ . Vậy đáp án A đúng.
Giả sử $\left( OMN \right)$ chứa đường thẳng $AB$ . Khi đó $O,B$ cùng thuộc mp$\left( AMN \right)$ . Suy ra $O,B$ cùng thuộc mp$\left( ACD \right)$ (vô lý). Đáp án B không thỏa mãn.
Giả sử $\left( MNO \right)$ đi qua điểm $A$ . Do $D,C$ lần lượt thuộc các đường thẳng $AN,AM$ nên$D,C$ thuộc mp$\left( AMN \right)$ . Như vậy 2 mp $\left( OCD \right),\left( AMN \right)$ trùng nhau. Suy ra $B$ thuộc mp$\left( ACD \right)$ (vô lý). Vậy đáp án C bị loại.
Tương tự ta cũng dễ dàng suy ra đáp án D bị loại.
Câu 19
Ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì :
[A]. Cùng thuộc một đường tròn
[B]. Cùng thuộc một đường thẳng
[C]. Cùng thuộc một eliP
[D]. Cùng thuộc một tam giác.
Đáp án B.
Giao tuyến của 2mp phân biệt là 1 đường thẳng, nên ba điểm phân biệt cùng thuộc 2 mp phân biệt sẽ nằm trên giao tuyến của 2mp phân biệt.
Câu 20
Cho hình chóp $S.ABCD$ có đáy là hình thang $ABCD$ ($AB$ là đáy lớn, $CD$ là đáy nhỏ). Khẳng định nào sau đây sai:
[A]. Hình chóp $S.ABCD$ có bốn mặt bên..
[B]. Giao tuyến của hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ là $SK$ trong đó $K$ là một điểm thuộc mặt phẳng $\left( ABCD \right)$ .
[C]. Giao tuyến của hai mặt phẳng $\left( SAC \right)$ và $\left( SBD \right)$ là $SO$ trong đó $O$ là giao điểm của hai đường thẳng $AC$ và $BD$
[D]. Giao tuyến của hai mặt phẳng $\left( SAD \right)$ và $\left( SBC \right)$ là $SI$ trong đó $I$ là giao điểm của $AD$ và $BC$ .
Đáp án B.
Hiển nhiên hình chóp $S.ABCD$ có 4 mặt bên nên đáp án A đúng.
Ta thấy giao tuyến của 2mp $\left( SAB \right),\left( ABCD \right)$ là $AB$ , $K$ là điểm thuộc cả hai mp do đó $K\in AB$ . tương tự ta cũng chứng minh được $K\in CD$ . Như vậy $K$ thuộc cả hai đường thẳng $AB,CD$ (vô lý do $AB,CD$ song song). Do vậy đáp án B sai.
$\begin{align}
& O\in AC\Rightarrow O\in \left( SAC \right). \\
& O\in BD\Rightarrow O\in \left( SBD \right). \\
\end{align}$
Do đó $O$ thuộc giao tuyến của hai mp $\left( SAC \right),\left( SBD \right)$ .
Tương tự ta cũng dễ thấy $SI=\left( SAD \right)\cap \left( SBC \right)$ .
Như vậy đáp án C,D đúng.
Câu 21
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là một tứ giác ($AB$ không song song $CD$ ). Gọi M là trung điểm của $SD,N$ là điểm nằm trên cạnh $SB$ sao cho $SN=2NB,O$ là giao điểm của $AC$ và $BD$ . Giả sử đường thẳng $d$ là giao tuyến của $\left( SAB \right)$ và $\left( SCD \right)$ . Nhận xét nào sau đây là sai:N
[A]. $d$ cắt $CD$.
[B]. $d$ cắt $MN$.
[C]. $d$ cắt $AB$.
[D]. $d$ cắt $SO$.
Đáp án B.
Gọi $I=AB\cap CD$ . Ta có:
$\left\{ \begin{align}
& I\in AB,AB\subset \left( SAB \right)\Rightarrow I\in \left( SAB \right) \\
& I\in CD,CD\subset \left( SCD \right)\Rightarrow I\in \left( SCD \right) \\
\end{align} \right.$$\Rightarrow I\in \left( SAB \right)\cap \left( SCD \right)$
Lại có $S\in \left( SAB \right)\cap \left( SCD \right).$
Do đó $SI=\left( SAB \right)\cap \left( SCD \right).$
$\Rightarrow d\equiv SI.$
Vậy $d$ cắt$AB,CD,SO$ .
Giả sử $d$ cắt $MN$ . Khi đó $M$ thuộc mp$\left( SAB \right)$ . Suy ra $D$ thuộc $\left( SAB \right)$ (vô lý). Vậy$d$ không cắt $MN$ . Đáp án B sai.
Câu 22
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành $\left( BC//AD \right)$ .Mặt phẳng $\left( P \right)$ di động chứa đường thẳng $AB$ và cắt các đoạn $SC,SD$ lần lượt tại $E,F$ . Mặt phẳng $\left( Q \right)$ di động chứa đường thẳng $CD$ và cắt $SA,SB$ lần lượt tại $G,H.\,I$ là giao điểm của $AE,BF;J$ là giao điểm của $CG,DH$ . Xét các mệnh đề sau:
$\left( 1 \right)$ Đường thẳng $EF$ luôn đi qua một điểm cố định..
$\left( 2 \right)$ Đường thẳng $GH$ luôn đi qua một điểm cố định.
$\left( 3 \right)$ Đường thẳng $IJ$ luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng?
[A]. $0$.
[B]. $1$.
[C]. $2$ .
[D]. $3$.
Đáp án D.
Trong mp$\left( ABCD \right)$ , gọi $M=AB\cap CD;O=AC\cap BD$ . Khi đó $M,O$ cố định.
Như vậy: $E,F,M$ cùng nằm trên hai mp $\left( P \right)$ và $\left( SCD \right)$ , do đó ba điểm $E,F,M$ thẳng hàng. Vậy đường thẳng $EF$ luôn đi qua một điểm cố định $M$ .
Tương tự, ta có $G,H,M$ cùng nằm trên hai mp $\left( Q \right)$ và $\left( SAB \right)$ ,do đó $G,H,M$ thẳng hàng. Vậy các đường thẳng $GH$ luôn đi qua một điểm cố định $M$ .
Do $\left\{ \begin{align}
& I\in AE\subset \left( SAC \right) \\
& I\in BF\subset \left( SBD \right) \\
\end{align} \right.$$\Rightarrow I\in \left( SAC \right)\cap \left( SBD \right)$ .
Tương tự ta cũng có $J\in \left( SAC \right)\cap \left( SBD \right);O\in \left( SAC \right)\cap \left( SBD \right)$
Do đó ba điểm $I,J,O$ thẳng hàng. Vậy $IJ$ luôn đi qua điểm cố định $O$ .
Vậy ta chọn đáp án D.
Câu 23
Cho tứ diện đều $ABCD$ có các cạnh bằng $a$ . Gọi $E$ là trung điểm $AB$ , $F$ là điểm thuộc cạnh $BC$ sao cho $BF=2FC,G$ là điểm thuộc cạnh $CD$ sao cho $CG=2GD$ . Tính độ dài đoạn giao tuyến của mặt phẳng $\left( EFG \right)$ với mặt phẳng $\left( ACD \right)$ của hình chóp $ABCD$ theo $a$ .
[A]. $\dfrac{\sqrt{19}}{15}a$.
[B]. $\dfrac{a\sqrt{141}}{30}$ .
[C]. $\dfrac{a\sqrt{34+15\sqrt{3}}}{15}$ .
[D]. $\dfrac{a\sqrt{34-15\sqrt{3}}}{15}$.
Đáp án A.
Trong mp $\left( BCD \right)$ , gọi $I=FG\cap BD$ .
Trong mp$\left( ADB \right)$ , gọi $H=IE\cap AD$ .
Khi đó $HG=\left( EFG \right)\cap \left( ACD \right)$ .
Áp dụng định lý Menelaus cho tam giác $BCD$ với ba điểm $I,G,F$ thẳng hàng ta có:
$\dfrac{ID}{IB}.\dfrac{FB}{FC}.\dfrac{GC}{GD}=1\Rightarrow \dfrac{ID}{IB}=\dfrac{1}{4}$
Áp dụng định lý Menelaus cho tam giác $ABD$ với ba điểm $I,H,E$ thẳng hàng ta có:
$\dfrac{HD}{HA}.\dfrac{EA}{EB}.\dfrac{IB}{ID}=1\Rightarrow \dfrac{HD}{HA}=\dfrac{1}{4}\Rightarrow HD=\dfrac{a}{5}$
Áp dụng định lý cosin vào tam giác $HDG$ ta có:
\[H{{G}^{2}}=H{{D}^{2}}+D{{G}^{2}}-2DH.DG.cos{{60}^{0}}=\dfrac{{{a}^{2}}}{25}+\dfrac{{{a}^{2}}}{9}-\dfrac{{{a}^{2}}}{15}=\dfrac{19{{a}^{2}}}{225}\Rightarrow HG=\dfrac{\sqrt{19}}{15}a\]
Câu 24
Cho tứ diện $ABCD,E$ nằm trên đoạn $BC$ sao cho $BC=3EC,F$ là điểm nằm trên $BD$ sao cho $CD=3DF$ . Gọi $G$ là giao điểm của $BF$ và $DE$ . Giao tuyến của hai mặt phẳng $\left( ACG \right)$ và $\left( ABD \right)$ là:
[A]. $AH$ trong đó $H$ thuộc $BD$ sao cho $\overrightarrow{BH}=-4\overrightarrow{HD}$
[B]. $AH$ trong đó $H$ thuộc $BD$ sao cho $\overrightarrow{BH}=\dfrac{1}{4}\overrightarrow{HD}$
[C]. $AH$ trong đó $H$ thuộc $BD$ sao cho $\overrightarrow{BH}=4\overrightarrow{HD}$
[D]. $AH$ trong đó $H$ thuộc $BD$ sao cho $\overrightarrow{BH}=-\dfrac{1}{4}\overrightarrow{HD}$
Đáp án C.
Trong $\left( BCD \right)$ , gọi $H=CG\cap BD$ .
Dễ thấy $H$ thuộc đoạn $BD$ nên $\overrightarrow{BH},\overrightarrow{HD}$ cùng hướng.
Do đó đáp án A, D bị loại.
Áp dụng định lý Ceva trong tam giác $BCD$ với $BF,DE,CH$ đồng quy ta có:
$\dfrac{EB}{EC}.\dfrac{FC}{FD}.\dfrac{HD}{HB}=1\Rightarrow 2.2.\dfrac{HD}{HB}=1\Rightarrow \dfrac{HD}{HB}=\dfrac{1}{4}\Rightarrow BH=4DH$
Do $\overrightarrow{BH},\overrightarrow{HD}$ cùng hướng nên $\overrightarrow{BH}=4\overrightarrow{HD}$ .
Câu 25
Cho tứ diện $SABC$ có $AB=c,BC=a,AC=b.\,\,\,AD,BE,CF$ là các đường phân giác trong của tam giác $ABC$ . Giao tuyến của hai mặt phẳng $\left( SBE \right)$ và $\left( SCF \right)$ là:
[A]. $SI$ trong đó $I$ thuộc $AD$ sao cho $\overrightarrow{AI}=\dfrac{b+c}{a}\overrightarrow{ID}$
[B]. $SI$ trong đó $I$ thuộc $AD$ sao cho $\overrightarrow{AI}=-\dfrac{b+c}{a}\overrightarrow{ID}$
[C]. $SI$ trong đó $I$ thuộc $AD$ sao cho $\overrightarrow{AI}=\dfrac{a}{b+c}\overrightarrow{ID}$
[D]. $SI$ trong đó $I$ thuộc $AD$ sao cho $\overrightarrow{AI}=\dfrac{-a}{b+c}\overrightarrow{ID}$
Đáp án A.
Do $I$ thuộc đoạn $AD$ nên $\overrightarrow{AI},\overrightarrow{ID}$ cùng hướng. Do đó B, D bị loại.
$AD$ là phân giác trong của tam giác $ABC$ nên theo tính chất đường phân giác ta có:
$\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\Rightarrow BD=\dfrac{ac}{b+c}$
Ta có: $BI$ là phân giác trong của tam giác $ABD$ nên theo tính chất đường phân giác ta có:
$\dfrac{IA}{ID}=\dfrac{BA}{BD}=\dfrac{b+c}{a}\Rightarrow IA=\dfrac{b+c}{a}ID$
Do đó: $\overrightarrow{AI}=\dfrac{b+c}{a}\overrightarrow{ID}$
Câu 26
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Gọi $M,N,P$ lần lượt là trung điểm của $AB,AD$ và $SO$ . Gọi $H$ là giao điểm của $SC$ với $\left( MNP \right)$ . Tính $\dfrac{SH}{SC}?$
[A]. $\dfrac{1}{3}$.
[B]. $\dfrac{1}{4}$.
[C]. $\dfrac{3}{4}$ .
[D]. $\dfrac{2}{3}$.
Đáp án B.
Trong mp $\left( ABCD \right)$ , gọi $I=MN\cap AO$ . Dễ thấy $H=PO\cap SC$ .
Do $MN$ là đường trung bình của tam giác $ABD$ nên $I$ là trung điểm AO. Suy ra $\dfrac{AI}{AC}=\dfrac{1}{4}$ và $PI$ là đường trung bình của tam giác $OSA$ . Do đó $IH//SA$ .
Áp dụng định lý Thales ta có: $\dfrac{SH}{SD}=\dfrac{AI}{AC}=\dfrac{1}{4}.$
Câu 27
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M,N$ lần lượt là trung điểm của $AD$ và $CD$ . Trên đường thẳng $DS$ lấy điểm $P$ sao cho $D$ là trung điểm $SP$ . Gọi $R$ là giao điểm của $SB$ với mặt phẳng $(MNP)$ . Tính $\dfrac{SR}{SB}\,?$
[A]. $\dfrac{1}{3}$ .
[B]. $\dfrac{1}{4}$ .
[C]. $\dfrac{3}{4}$.
[D]. $\dfrac{2}{5}$.
Đáp án D.
Trong mp$(ABCD)$, gọi $I=BD\cap MN,O=AC\cap BD$ .
Dễ thấy $R=IP\cap SB$.
Do $MN$ là đường trung bình của tam giác $ABD$ nên $I$ là trung điểm DO. Suy ra $\dfrac{DI}{IB}=\dfrac{1}{3}$.
Áp dụng định lý Menelaus vào taam giác $SBD$ ta có :
$\dfrac{BR}{RS}.\dfrac{PS}{PD}.\dfrac{BI}{ID}=1\Rightarrow \dfrac{BR}{RS}.2.\dfrac{1}{3}=1\Rightarrow \dfrac{SR}{SB}=\dfrac{2}{3}$
Câu 28
Cho tứ diện $SABC,E,F$ lần lượt thuộc đoạn $AC,AB.$ Gọi $K$ là giao điểm của $BE$ và $CF$ . Gọi $D$ là giao điểm của $\left( SAK \right)$ với $BC$ . Mệnh đề nào sau đây đúng?
[A]. $\dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}\ge 6$.
[B]. $\dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}\le 6$.
[C]. $\dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}>6$.
[D]. $\dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}<6$.
Đáp án A.
Nếu K trùng với trọng tâm G thì $\dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}=6$ . Do đó C, D bị loại.
Ta có $\dfrac{DK}{DA}+\dfrac{EK}{EB}+\dfrac{FK}{FC}=\dfrac{{{S}_{KBC}}}{{{S}_{ABC}}}+\dfrac{{{S}_{KAC}}}{{{S}_{ABC}}}+\dfrac{{{S}_{KAB}}}{{{S}_{ABC}}}=1$
Áp dụng định lý bất đẳng thức Cauchy ta có:
$\begin{align}
& \left( \dfrac{DK}{DA}+\dfrac{EK}{EB}+\dfrac{FK}{FC} \right)\left( \dfrac{DA}{DK}+\dfrac{EB}{EK}+\dfrac{FC}{FK} \right)\ge 9 \\
& \Rightarrow \dfrac{DA}{DK}+\dfrac{EB}{EK}+\dfrac{FC}{FK}\ge 9\Rightarrow \dfrac{AK}{KD}+\dfrac{BK}{KE}+\dfrac{CK}{KF}\ge 6 \\
\end{align}$
Câu 29
Cho hình chóp $S.ABCD,\,\,D,M$ lần lượt là trung điểm của $BC,AD$ . Gọi $E$ là giao điểm của $\left( SBM \right)$ với $AC,\,\,F$ là giao điểm của $\left( SCM \right)$ với $AB$ . Tính $\dfrac{MF}{CM-ME}+\dfrac{ME}{BM-ME}$ ?
[A]. $1$.
[B]. $2$.
[C]. $\dfrac{1}{2}$
[D]. $\dfrac{1}{3}$ .
Đáp án A.
Ta có : $\dfrac{BM}{ME}=\dfrac{{{S}_{ABM}}}{{{S}_{AME}}}=\dfrac{{{S}_{CBM}}}{{{S}_{CME}}}=\dfrac{{{S}_{ABM}}+{{S}_{CBM}}}{{{S}_{AME}}+{{S}_{CME}}}=\dfrac{{{S}_{ABM}}+{{S}_{CBM}}}{{{S}_{AME}}}=\dfrac{BD}{CD}+\dfrac{BF}{FA}$
$\Rightarrow \dfrac{BF}{AF}=\dfrac{BM}{ME}-1=\dfrac{BM-ME}{ME}\left( 1 \right)$ .
Tương tự ta cũng chứng minh được: $\dfrac{CM}{MF}=\dfrac{CE}{AE}+\dfrac{CD}{BD}\Rightarrow \dfrac{CE}{AE}=\dfrac{CM}{MF}-1=\dfrac{CM-MF}{MF}\left( 2 \right)$
Và $1=\dfrac{AM}{MD}=\dfrac{AE}{CE}+\dfrac{AF}{BF}\left( 3 \right)$
Từ (1,2,3) suy ra $\dfrac{MF}{CM-MF}+\dfrac{ME}{BM-ME}=1$
Câu 30
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Một mặt phẳng $\left( \alpha \right)$ cắt các cạnh bên $SA,SB,SC,SD$ tương ứng tại các điểm $E,\,\,F,\,\,G,\,\,H$ . Gọi $I=AC\cap BD,J=EG\cap SI$ . Mệnh đề nào sau đây đúng?
[A]. $\dfrac{SA}{SE}+\dfrac{SC}{SG}=\dfrac{SB}{SF}+\dfrac{SD}{SH}$.
[B]. $\dfrac{SA}{SE}+\dfrac{SC}{SG}\ge 2\dfrac{SI}{SJ}$.
[C]. $\dfrac{SA}{SE}+\dfrac{SC}{SG}>\dfrac{SB}{SF}+\dfrac{SD}{SH}$ .
[D]. $\dfrac{SB}{SF}+\dfrac{SD}{SH}\ge 2\dfrac{SI}{SJ}$.
Đáp án A.
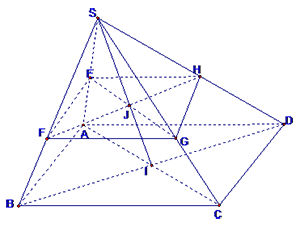
Xét trường hợp đặc biệt $E,F,G,H$ lần lượt là trung điểm của SA, SB, SC, S[D]. Khi đó ta dễ dàng loại được đáp án D.
Dựng $AT//EG\left( T\in SI \right),CK//EG\left( KESI \right)$
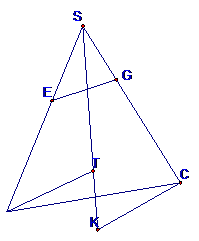
Theo định lý Thales, ta có:
$\dfrac{SA}{SE}=\dfrac{ST}{SJ},\dfrac{SC}{SG}=\dfrac{SK}{SJ};\dfrac{IT}{IK}=\dfrac{IA}{IC}=1$
Suy ra: $\dfrac{SA}{SE}+\dfrac{SC}{SG}=\dfrac{ST+SK}{SJ}=\dfrac{SI-IT+SI+IK}{SJ}=2\dfrac{SI}{SJ}$
Như vậy, ý B bị loại.
Tương tự, ta chứng minh được $\dfrac{SB}{SF}+\dfrac{SD}{SH}=2\dfrac{SI}{SJ}.$
Từ đây ta thấy ngay ý C bị loại và A là đáp án A là đáp án lựa chọn.
Chú ý: Cho tam giác AB[C]. Gọi O là trung điểm AC, M, N là hai điểm nằm trên cạnh AB, A[C]. MN cắt BO tại I. Khi đó: $\dfrac{BA}{BM}+\dfrac{BC}{BN}=\dfrac{2BO}{BI}$ .
Câu 31
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Gọi $M,N$ lần lượt là các điểm nằm trên cạnh $AB,AD$ sao cho $\dfrac{BM}{MA}=\dfrac{2}{3},\dfrac{NC}{BN}=\dfrac{1}{2}$ . Gọi $P$ là điểm trên cạnh $SD$ sao cho $\dfrac{PD}{PS}=\dfrac{1}{5}$ . $J$ là giao điểm của $SO$ với $\left( MNP \right)$ . Tính $\dfrac{SJ}{SO}\,\,\,?$
[A]. $\dfrac{10}{11}$ .
[B]. $\dfrac{1}{11}$.
[C]. $\dfrac{3}{4}$.
[D]. $\dfrac{5}{2}$.
Đáp án A.
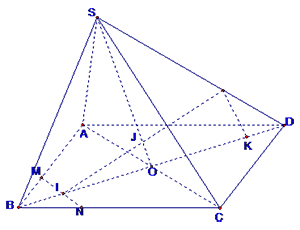
Theo chú ý câu 30 ta có: $\dfrac{BA}{BM}+\dfrac{BC}{BN}=\dfrac{5}{2}+\dfrac{3}{2}=4\Rightarrow \dfrac{2BO}{BI}=4\Rightarrow \dfrac{BO}{BI}=2\Rightarrow \dfrac{OI}{BO}=\dfrac{1}{2}\Rightarrow \dfrac{OI}{OD}=\dfrac{1}{2}$ .
Áp dụng định lý Menelaus trong tam giác $SOD$ ta có: $\dfrac{IO}{ID}.\dfrac{PD}{PS}.\dfrac{JS}{JO}=1\Rightarrow \dfrac{JS}{JO}=10\Rightarrow \dfrac{SJ}{SO}=\dfrac{10}{11}$
Câu 32
Cho tứ diện $ABCD$ . $E$ là điểm thuộc đoạn $AB$ sao cho $EA=2EB.\,\,F,G$ là các đei63m thuộc đường thẳng $BC$ sao cho $\overrightarrow{FC}=5\overrightarrow{FB},\overrightarrow{GC}=-5\overrightarrow{GB}.\,\,H,I\,$ là các điểm thuộc đường thẳng $CD$ sao cho $\overrightarrow{HC}=-5\overrightarrow{HD},\overrightarrow{ID}=-5\overrightarrow{IC},\,J$ thuộc tia đối của tia $DA$ sao cho $D$ là trung điểm của $AJ$ . Trong các mệnh đề sau, mệnh đề nào đúng?
[A]. Bốn điểm $E,F,H,J$ đồng phẳng
[B]. Bốn điểm $E,F,I,J$ đồng phẳng.
[C]. Bốn điểm $E,G,H,I$ đồng phẳng.
[D]. Bốn điểm $E,G,I,J$ đồng phẳng.
Đáp án A.
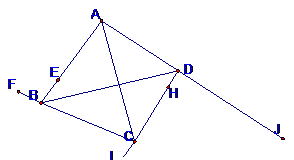
Dựa vào nhận xét ví dụ 2, ta có:
$\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BF}}{\overline{CF}}.\dfrac{\overline{CH}}{\overline{DH}}.\dfrac{\overline{DJ}}{\overline{AJ}}=-2.\dfrac{1}{5}.\left( -5 \right).\dfrac{1}{2}=1$ nên $E,F,H,J$ đồng phẳng.
$\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BF}}{\overline{CF}}.\dfrac{\overline{CI}}{\overline{DI}}.\dfrac{\overline{DJ}}{\overline{AJ}}=-2.\dfrac{1}{5}.\left( \dfrac{1}{5} \right).\dfrac{1}{2}=\dfrac{1}{25}$ nên $E,F,I,J$ không đồng phẳng.
$\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BG}}{\overline{CG}}.\dfrac{\overline{CH}}{\overline{DH}}.\dfrac{\overline{DJ}}{\overline{AJ}}=-2.\left( -\dfrac{1}{5} \right).\left( -5 \right).\dfrac{1}{2}=-1$ nên $E,G,H,J$ không đồng phẳng.
$\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BG}}{\overline{CG}}.\dfrac{\overline{CI}}{\overline{DI}}.\dfrac{\overline{DJ}}{\overline{AJ}}=-2.\left( -\dfrac{1}{5} \right).\left( \dfrac{1}{5} \right).\dfrac{1}{2}=\dfrac{1}{25}$ nên $E,G,I,J$ không đồng phẳng.
Câu 33
Cho tứ diện $ABCD,\,E,\,U$ là điểm thuộc đường thẳng $AB$ sao cho $\overrightarrow{EA}=-2\overrightarrow{EB},\,\,5\overrightarrow{UA}=4\overrightarrow{UB.}\,\,F,G$ là các điểm thuộc đường thẳng $BC$ sao cho $\overrightarrow{FC}=5\overrightarrow{FB},\,\,\overrightarrow{GC}=-2\overrightarrow{GB}.\,\,H,I\,$ là các điểm thuộc đường thẳng $CD$ sao cho \[\overrightarrow{HC}=-5\overrightarrow{HD},\,\overrightarrow{ID}=5\overrightarrow{IC}.\,J,\,K\] là các điểm nằm trên đường thẳng $DA$ sao cho $\overrightarrow{JA}=2\overrightarrow{JD},\overrightarrow{KD}=5\overrightarrow{KA}$ . Bốn điểm nào dưới đây lập nên một tứ diện?
[A]. $E,F,H,J$.
[B]. $E,G,I,K$.
[C]. $U,G,H,J$.
[D]. $U,F,I,K$.
Đáp án D.
Dựa vào nhận xét ví dụ 2, ta có:
$\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BF}}{\overline{CF}}.\dfrac{\overline{CH}}{\overline{DH}}.\dfrac{\overline{DJ}}{\overline{AJ}}=-2.\dfrac{1}{5}.\left( -5 \right).\dfrac{1}{2}=1$ nên $E,F,H,J$ đồng phẳng.
\[\dfrac{\overline{AE}}{\overline{BE}}.\dfrac{\overline{BG}}{CG}.\dfrac{\overline{CI}}{\overline{DI}}.\dfrac{\overline{DK}}{\overline{AK}}=-2.\left( -\dfrac{1}{2} \right).\left( 5 \right).\dfrac{1}{5}=1\] nên $E,G,I,K$ đồng phẳng.
$\dfrac{\overline{AU}}{\overline{BU}}.\dfrac{\overline{BG}}{\overline{CG}}.\dfrac{\overline{CH}}{\overline{DH}}.\dfrac{\overline{DJ}}{\overline{AJ}}=\dfrac{4}{5}.\left( -\dfrac{1}{2} \right).\left( -5 \right).\dfrac{1}{2}=1$ nên $U,G,H,J$ đồng phẳng.
$\dfrac{\overline{AU}}{\overline{BU}}.\dfrac{\overline{BF}}{\overline{CF}}.\dfrac{\overline{CI}}{\overline{DI}}.\dfrac{\overline{DK}}{\overline{AK}}=\dfrac{4}{5}.\left( \dfrac{1}{5} \right).\left( 5 \right).\dfrac{1}{5}=\dfrac{4}{25}$ nên $U,F,I,K$ không đồng phẳng. Do đó 4 điểm này lập nên 1 tứ diện.
Câu 34
Cho tứ diện $ABCD$ có $M,N$ lần lượt là trung điểm của $AB,CD$ và $P$ là điểm thuộc cạnh $BC$ ($P$ không là trung điểm $BC$ ).
a) Thiết diện của tứ diện bị cắt bởi $\left( MNP \right)$ là:
[A]. Tam giác
[B]. Tứ giác
[C]. Ngũ giác.
[D]. Lục giác.
b) Gọi $Q$ là giao điểm của $\left( MNP \right)$ với $AD,\,\,I$ là giao điểm của $MN$ với $PQ$ . Mệnh đề nào sau đây đúng?
[A]. ${{S}_{MNPQ}}=2{{S}_{MPN}}$ .
[B]. ${{S}_{MNPQ}}=2{{S}_{MPQ}}$.
[C]. . ${{S}_{MNPQ}}=4{{S}_{MPI}}$
[D]. ${{S}_{MNPQ}}=4{{S}_{PIN}}$ .
Đáp án B, A.
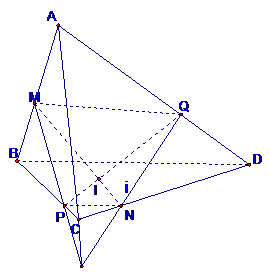
a)Do tứ diện ABCD có 4 mặt nên thiết diện không thể là ngũ giác hay lục giác. Nó chỉ có thể là tam giác hoặc tứ giác.
Trong mp $\left( ABC \right)$ , gọi $K=MP\cap AC$ (P không phải là trung điểm đoạn BC nên MP cắt AC)
Trong mp$\left( ACD \right)$ , gọi $Q=KN\cap AD$
Do $Q\in KN\subset \left( MNP \right)$ nên $Q=\left( MNP \right)\cap AD$
Ta có: $\left\{ \begin{align}
& \left( MNP \right)\cap \left( ABD \right)=MQ \\
& \left( MNP \right)\cap \left( ABC \right)=MP \\
& \left( MNP \right)\cap \left( BCD \right)=PN \\
& \left( MNP \right)\cap \left( ACD \right)=NQ \\
\end{align} \right.$
Suy ra thiết diện cần tìm là tứ giác $MPNQ.$
Ta chọn đáp án B.
b)Áp dụng ví dụ 11, do $M,N,P,Q$ đồng phẳng nên $\dfrac{AM}{BM}.\dfrac{BP}{CP}.\dfrac{CN}{DN}.\dfrac{DQ}{AQ}=1\Rightarrow \dfrac{BP}{CP}.\dfrac{DQ}{AQ}=1$
(Do M, N lần lượt là trung điểm của AB, CD) . Từ đây suy ra $\dfrac{BP}{CP}=\dfrac{AQ}{DQ}.$
Giả sử $\dfrac{BP}{PC}=k$ . Khi đó ta suy ra $\overrightarrow{BP}=k\overrightarrow{PC},\overrightarrow{AQ}=k\overrightarrow{QD}$
Suy ra $\overrightarrow{BP}+\overrightarrow{AQ}=-k\left( \overrightarrow{CP}+\overrightarrow{QD} \right)\left( 1 \right)$
Do J là trung điểm của PQ.
Ta có: $\left\{ \begin{align}
& \overrightarrow{MJ}=\overrightarrow{MB}+\overrightarrow{BP}+\overrightarrow{PJ} \\
& \overrightarrow{MJ}=\overrightarrow{MA}+\overrightarrow{AQ}+\overrightarrow{QJ} \\
\end{align} \right.\Rightarrow 2\overrightarrow{MJ}=\overrightarrow{AQ}+\overrightarrow{BP}\left( 2 \right)$
Chứng minh tương tự ta cũng có: $2\overrightarrow{NJ}=\overrightarrow{CP}+\overrightarrow{DQ}\left( 3 \right)$
Từ (1,2,3) suy ra $\overrightarrow{MJ}=-k\overrightarrow{NJ}$ . Điều này dẫn đến M, N, J thẳng hàng. Như vậy I trùng J.
Điều này suy ra ${{S}_{MNPQ}}=2{{S}_{MPN}}$ .
Chọn đáp án A.
Câu 35
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, $E$ là trung điểm của $SA,F,G$ lần lượt là các điểm thuộc cạnh $BC,CD$ . Thiết diện của hình chóp cắt bởi $\left( MNP \right)$ là:
[A]. Tam giác
[B]. Tứ giác
[C]. Ngũ giác.
[D]. Lục giác.
Đáp án C.
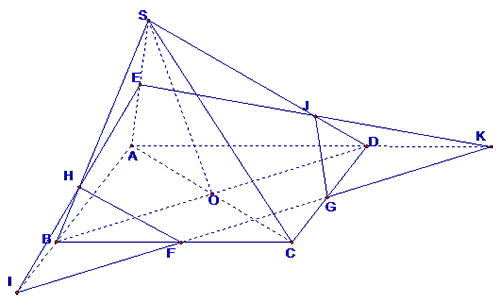
Trong mp$\left( ABCD \right)$ , gọi $I=FG\cap AB;K=FG\cap AD$
Trong mp$\left( SAB \right)$ , gọi $H=IE\cap SB$
Trong mp$\left( SAD \right)$ , gọi $J=EK\cap SD$.
Ta có: \[\begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=FG, \\
& \left( EFG \right)\cap \left( SCD \right)=GJ \\
& \left( EFG \right)\cap \left( SAD \right)=JE \\
& \left( EFG \right)\cap \left( SAB \right)=HE \\
& \left( EFG \right)\cap \left( SBC \right)=HF \\
\end{align}\]
Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$
Câu 36
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang với đáy lớn $AD,E$ là trung điểm của cạnh $SA,F,G$ là các điểm thuộc cạnh $SC,AB$ ($F$ không là trung điểm của $SC$ ). Thiết diện của hình chóp cắt bởi mặt phẳng $\left( EFG \right)$ là:
[A]. Tam giác
[B]. Tứ giác
[C]. Ngũ giác.
[D]. Lục giác.
Đáp án C.
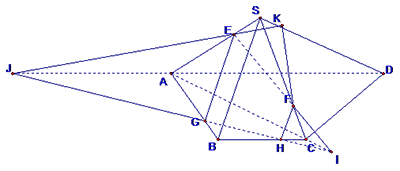
Trong mp$\left( SAC \right)$ , Gọi $I=EF\cap AC$
Trong mp$\left( ABCD \right)$ , Gọi $H=IG\cap BC,J=IG\cap AB$
Trong mp$\left( SAD \right)$ , Gọi $K=JE\cap SD$
Khi đó ta có:$\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=GH, \\
& \left( EFG \right)\cap \left( SCD \right)=KF \\
& \left( EFG \right)\cap \left( SAD \right)=EK \\
& \left( EFG \right)\cap \left( SAB \right)=GE \\
& \left( EFG \right)\cap \left( SBC \right)=HF \\
\end{align} \right.$
Do đó ngũ giác EKFHG là thiết diện của hình chóp cắt bởi $\left( EFG \right)$
Câu 37
Cho hình chóp $S{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ với đáy là đa giác lồi ${{A}_{1}}{{A}_{2}}…{{A}_{n}}\,\,\left( n\ge 3,n\in \mathbb{N} \right).$ Trên tia đối của tia ${{A}_{1}}S$ lấy điểm ${{B}_{1}},{{B}_{2}},…{{B}_{n}}$ là các điểm nằm trên cạnh $S{{A}_{2}},S{{A}_{n}}$ . Thiết diện của hình chóp cắt bởi mặt phẳng $\left( {{B}_{1}}{{B}_{2}}{{B}_{n}} \right)$ là:
[A]. Đa giác $n-2$ cạnh.
[B]. Đa giác $n-1$ cạnh.
[C]. Đa giác $n$ cạnh.
[D]. Đa giác $n+1$ cạnh.
Đáp án D.
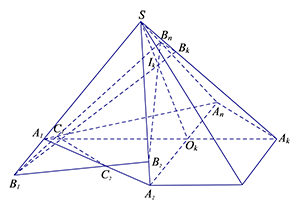
Trong mặt phẳng $\left( S{{A}_{1}}{{A}_{2}} \right)$ gọi ${{C}_{2}}$ là giao điểm của ${{B}_{1}}{{B}_{2}}$ với ${{A}_{1}}{{A}_{2}}$.
Trong mặt phẳng $\left( S{{A}_{1}}{{A}_{n}} \right)$ gọi ${{C}_{n}}$ là giao điểm của ${{B}_{1}}{{B}_{n}}$ với ${{A}_{1}}{{A}_{n}}$.
Trong mặt phẳng $\left( {{A}_{1}}{{A}_{2}}…{{A}_{n}} \right)$ gọi ${{O}_{k}}$ $\left( k=3,4,…,n-1 \right)$ là giao điểm của ${{A}_{1}}{{A}_{k}}$ với ${{A}_{2}}{{A}_{n}}$.
Trong mặt phẳng $\left( S{{A}_{2}}{{A}_{n}} \right)$, gọi ${{I}_{k}}$ $\left( k=3,4,…,n-1 \right)$ là giao điểm của $S{{O}_{k}}$ với ${{B}_{2}}{{B}_{n}}$.
Trong mặt phẳng $\left( S{{A}_{1}}{{A}_{k}} \right)$, gọi ${{B}_{k}}$ $\left( k=3,4,…,n-1 \right)$ là giao điểm của $S{{A}_{k}}$ với ${{B}_{1}}{{I}_{k}}$.
Do ${{B}_{k}}\in {{B}_{1}}{{I}_{k}}\subset \left( {{B}_{1}}{{B}_{2}}{{B}_{n}} \right)$ nên ${{B}_{k}}$ là giao điểm của \[S{{A}_{k}}\] $\left( k=3,4,…,n-1 \right)$ với mặt phẳng $\left( {{B}_{1}}{{B}_{2}}{{B}_{n}} \right)$.
Vậy thiết diện của hình chóp cắt bởi $\left( {{B}_{1}}{{B}_{2}}{{B}_{n}} \right)$ là đa giác ${{C}_{2}}{{B}_{2}}…{{B}_{n}}{{C}_{n}}$.
Câu 38
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, E là điểm thuộc cạnh bên SD sao cho $SD=3SE$ . F là trọng tâm tam giác $SAB,\,G$ là điểm thay đổi trên cạnh B[C]. Thiết diện cắt bởi mặt phẳng $\left( EFG \right)$ là:
[A]. Tam giác
[B]. Tứ giác
[C]. Ngũ giác.
[D]. Lục giác.
Đáp án C.
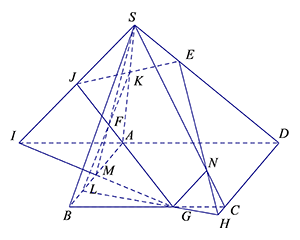
Cách 1:
Gọi $M$ là trung điểm của $AB$, khi đó $S$, $F$, $M$ thẳng hàng.
Trong mặt phẳng $\left( ABCD \right)$, gọi $I$ là giao điểm của $MG$ với $AD$. Khi đó $SI=\left( SMG \right)\cap \left( SAD \right)$.
Trong mặt phẳng $\left( SMG \right)$, gọi $J$ là giao điểm của $FG$ với $SI$. Ta thấy $J$ thuộc $FG$ nên $J$ thuộc $\left( EFG \right)$. Trong $\left( SAD \right)$, gọi $K$ là giao điểm của $JE$ với $SA$. Trong mặt phẳng $\left( SAB \right)$, gọi $L$ là giao điểm của $KF$ với $AB$.
Trong mặt phẳng $\left( ABCD \right)$, gọi $H$ là giao điểm của $LG$ với $CD$. Trong mặt phẳng $\left( SCD \right)$, gọi $N$ là giao điểm của $EH$ với $SC$.
Ta có: \[\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=LG;\left( EFG \right)\cap \left( SBC \right)=GN \\
& \left( EFG \right)\cap \left( SCD \right)=NE;\left( EFG \right)\cap \left( SAD \right)=EK \\
& \left( EFG \right)\cap \left( SAB \right)=KL \\
\end{align} \right.\] .
Vậy ngũ giác $LGNEK$ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$.
Chú ý: Mấu chốt của ví dụ trên là việc dựng được điểm $J$ là giao điểm của $FG$ với $\left( SAD \right)$ (thông qua việc dựng giao tuyến $SI$ của mặt phẳng $\left( SFG \right)$ với mặt phẳng $\left( SAD \right)$). Có thể dựng thiết diện trên bằng nhiều cách với việc dựng giao điểm (khác $E,F,G$) của một trong các đường thẳng \[EF,FG\]; hoặc $GE$ với một mặt của hình chóp. Sau đây, tôi xin trình bày cách hai, điểm mấu chốt là xác định giao điểm của \[EF\] với mặt phẳng $\left( ABCD \right)$.
Cách 2:

Trong mặt phẳng $\left( SMD \right)$, gọi $P$ là giao điểm của $EF$ với $MD$.
Trong mặt phẳng $\left( ABCD \right)$, gọi $H,L$ là giao điểm của $P,G$ với $CD$, $AB$.
Trong mặt phẳng $\left( SAB \right)$, gọi $K$ là giao điểm của $LF$ với $SA$.
Trong mặt phẳng \[\left( SCD \right)\], gọi $N$ là giao điểm của $EH$ với $SC$.
Ta có: \[\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=LG;\left( EFG \right)\cap \left( SBC \right)=GN \\
& \left( EFG \right)\cap \left( SCD \right)=NE;\left( EFG \right)\cap \left( SAD \right)=EK \\
& \left( EFG \right)\cap \left( SAB \right)=KL \\
\end{align} \right.\].
Vậy ngũ giác $LGNEK$ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$.
Câu 39
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang với đáy lớn AD, E là một điểm thuộc mặt bên $\left( SCD \right)$ . F, G lần lượt là các điểm thuộc cạnh AB và SB. Thiết diện của hình chóp $S.ABCD$ cắt bởi mặt phẳng $\left( EFG \right)$ có thể là:
[A]. Tam giác, tứ giác .
[B]. Tứ giác, ngũ giác.
[C]. Tam giác, ngũ giác.
[D]. Ngũ giác.
Đáp án B.
Trong mặt phẳng $\left( ABCD \right)$, gọi $H$ là giao điểm của $AB$ và $CD$. Trong mặt phẳng $\left( SAB \right)$, gọi $I$ là giao điểm của $FG$ và $SH$.
Xét các trường hợp sau:
Trường hợp 1:
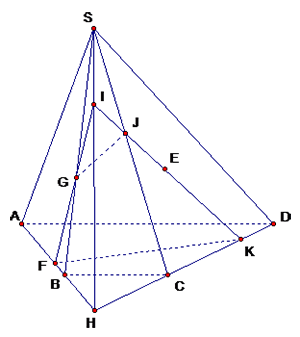
Trong mặt phẳng $\left( SCD \right)$ , $IE$ cắt $SC$ tại $J$ và cắt đoạn $CD$ tại $K$.
Ta có $J\in IE\subset \left( EFG \right)$ nên $J$ là giao điểm của $\left( EFG \right)$ với $SC$ ,
$K\in IE\subset \left( EFG \right)$ nên $K$ là giao điểm của $\left( EFG \right)$ với $CD$.
Ta có $\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=FK;\,\,\left( EFG \right)\cap \left( SAB \right)=FG \\
& \left( EFG \right)\cap \left( SBC \right)=GJ;\,\,\,\left( EFG \right)\cap \left( SCD \right)=JK \\
\end{align} \right.$
Suy ra tứ giác $KFGJ$ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$.
Trường hợp 2:
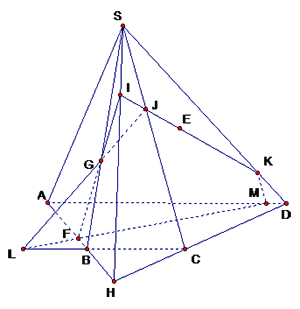
Trong mặt phẳng $\left( SCD \right)$ , $IE$ cắt $SC$ tại $J$ và cắt đoạn $SD$ tại $K$(cắt $CD$ tại một điểm nằm ngoài đoạn $CD$).
Trong mặt phẳng $\left( SBC \right)$ :
Nếu $GJ$ song song với $BC$ thì ta có: $\dfrac{BG}{G\text{S}}=\dfrac{CJ}{J\text{S}}$ . Gọi $T$ là giao điểm của $IE$ với $CD$ .
Áp dụng định lí Menelaus vào các tam giác $SBH$ và $SCH$ ta có
$\dfrac{FB}{FH}.\dfrac{IH}{IS}.\dfrac{G\text{S}}{GB}=1=\dfrac{TC}{TH}.\dfrac{IH}{IS}.\dfrac{J\text{S}}{JC}\Rightarrow \dfrac{FB}{FH}=\dfrac{TC}{TH}$ . Điều này chỉ xảy ra khi $T$ thuộc đoạn $CD$ (vô lí)
Do vây $GJ$ cắt $BC$ , giả sử tại $L$.
Trong mặt phẳng $\left( ABCD \right)$ , gọi $M$ là giao điểm của $LF$ với $AD$ .
Ta có $\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=FM;\,\,\left( EFG \right)\cap \left( SAB \right)=FG \\
& \left( EFG \right)\cap \left( SBC \right)=GJ;\,\,\,\left( EFG \right)\cap \left( SCD \right)=JK \\
& \left( EFG \right)\cap \left( SAD \right)=KM \\
\end{align} \right.$
Suy ra ngũ giác $KJGFM$ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$ .
Vậy thiết diện của hình chóp $S.ABCD$ cắt bởi mặt phẳng $\left( EFG \right)$ hoặc là tứ giác hoặc là ngũ giác.
Câu 40
Cho hình chóp $S.ABCD,\,\,E$ là trung điểm của $SB,\,F$ thuộc SC sao cho $3\overrightarrow{SF}=2\overrightarrow{SC},\,\,G$ là một điểm thuộc miền trong tam giác $SAD$ . Thiết diện của hình chóp cắt bởi mặt phẳng $\left( EFG \right)$ là:
[A]. Tam giác, tứ giác .
[B]. Tứ giác, ngũ giác.
[C]. Tam giác, ngũ giác.
[D]. Ngũ giác.
Đáp án B.
Trong mặt phẳng $\left( SBC \right)$ , gọi $J$ là giao điểm của $EF$ với $BC$ . Trong mặt phẳng $\left( SAD \right)$ , gọi $I$ là giao điểm của $SG$ với \[AD\] . Trong mặt phẳng $\left( ABCD \right)$ , gọi $N$ là giao điểm của \[IJ\] với $CD$ . Trong mặt phẳng $\left( SIJ \right)$ , gọi $K$ là giáo điểm của $JG$ với $SN$ .
Trong mặt phẳng $\left( SCD \right)$ , có hai khả năng xảy ra như sau:
Trường hợp 1: $FK$ cắt đoạn $CD$ tại $P$ .

Trong mặt phẳng $\left( ABCD \right)$ , gọi $Q$ là giao điểm của $JP$ với $AD$. Trong mặt phẳng $\left( SAD \right)$ , gọi $R$ là giao điểm của $QG$ với $SA$ .
Ta có $\left\{ \begin{align}
& \left( EFG \right)\cap \left( ABCD \right)=PQ;\,\,\left( EFG \right)\cap \left( SAD \right)=QR \\
& \left( EFG \right)\cap \left( SAB \right)=RE;\,\,\,\left( EFG \right)\cap \left( SBC \right)=EF \\
& \left( EFG \right)\cap \left( SCD \right)=FP \\
\end{align} \right.$
Trường hợp này , ngũ giác \[REFPQ\] là thiết diện của hình chóp $S.ABCD$ cắt bởi $\left( EFG \right)$.
Trường hợp 2: $FK$ cắt $SD$ tại $H$ ($FK$ không cắt đoạn $CD$ ).
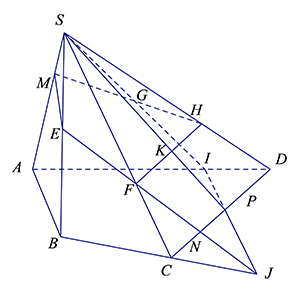
Trong mặt phẳng $\left( SAD \right)$ , gọi $M$ là giao điểm của $HG$ với $SA$ ($HG$ không thể cắt đoạn $AD$ vì giả sử ngược lại $HG$ cắt cạnh $AD$ tại $O$ , khi đó $JO$ sẽ cắt cạnh $CD$ (vô lí vì $\left( EFG \right)$ đã cắt cạnh $SC,\,SD$ )).
Khi đó $\left\{ \begin{align}
& \left( EFG \right)\cap \left( SCD \right)=FH;\,\,\left( EFG \right)\cap \left( SAD \right)=MH \\
& \left( EFG \right)\cap \left( SAB \right)=ME;\,\,\,\left( EFG \right)\cap \left( SBC \right)=EF \\
\end{align} \right.$
Trường hợp này, tứ giác $MEFH$ là thiết diện của hình chóp cắt bởi $\left( EFG \right)$.
Câu 41
Cho hình tứ diện $ABCD$ có tất cả các cạnh bằng $6a$ . Gọi M, N lần lượt là trung điểm của CA, C[B]. P là điểm trên cạnh BD sao cho $BP=2PD$ . Diện tích S thiết diện của tứ diện $ABCD$ bị cắt bởi $\left( MNP \right)$ là:
[A]. $S=\dfrac{5{{a}^{2}}\sqrt{51}}{4}$.
[B]. $S=\dfrac{5{{a}^{2}}\sqrt{147}}{4}$.
[C]. $S=\dfrac{5{{a}^{2}}\sqrt{147}}{2}$.
[D]. $S=\dfrac{5{{a}^{2}}\sqrt{51}}{2}$.
Đáp án A.
Trong mặt phẳng $\left( BCD \right)$, gọi $I$ là giao điểm của $NP$ với $CD$.
Trong mặt phẳng $\left( ACD \right)$, gọi $Q$ là giao điểm của $AD$ và $MI$. Suy ra $Q$ là giao điểm của $AD$ với $\left( MNP \right)$. Khi đó, tứ giác $MNPQ$ là thiết diện của tứ diện cắt bởi mặt phẳng $\left( MNP \right)$.
Trong tam giác $BCI$ ta có $P$ là trọng tâm của tam giác suy ra $D$ là trung điểm của $CI$.
Trong tam giác $ACI$ có $Q$ là trọng tâm của tam giác nên $\dfrac{QA}{QD}=2$.
Ta có $\dfrac{IP}{IN}=\dfrac{IQ}{IM}=\dfrac{2}{3}\Rightarrow PQ//MN$.
Suy ra $MNPQ$ là hình thang với đáy lớn $MN$.
Ta có: $AQ=4a,\,AM=3a=MN,\,PQ=2a.$ Áp dụng định lí cosin trong tam giác $MAQ$ ta có:
$M{{Q}^{2}}=A{{M}^{2}}+A{{Q}^{2}}-2AM.AQ.\cos \,{{60}^{0}}=16{{a}^{2}}+9{{a}^{2}}-12{{a}^{2}}=13{{a}^{2}}\Rightarrow MQ=a\sqrt{13}$.
Tương tự ta cũng tính được $NP=a\sqrt{13}$.
Dễ thấy $MNPQ$ là hình thang cân. Do đó:
$S=\dfrac{\left( MN+PQ \right)\sqrt{M{{Q}^{2}}-{{\left( \dfrac{MN-PQ}{2} \right)}^{2}}}}{2}=\dfrac{5{{a}^{2}}\sqrt{51}}{4}$.
Câu 42
Cho tứ diện $ABCD$ có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F sao cho $CE=a,\,DF=a$ . Gọi M là trung điểm của đoạn A[B]. Diện tích S thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $\left( MEF \right)$ là:
[A]. $S=\dfrac{{{a}^{2}}\sqrt{33}}{18}$.
[B]. $S=\dfrac{{{a}^{2}}}{3}$.
[C]. $S=\dfrac{{{a}^{2}}}{6}$.
[D]. $S=\dfrac{{{a}^{2}}\sqrt{33}}{9}$.
Đáp án C.
Trong mặt phẳng $\left( ABC \right)$, gọi $H$ là giao điểm của $ME$ với $AC$.
Trong mặt phẳng $\left( ABD \right)$, gọi $K$ là giao điểm của $MF$ và $AD$.
Ta có: $\left\{ \begin{align}
& \left( MEF \right)\cap \left( ABC \right)=MH \\
& \left( MEF \right)\cap \left( ABD \right)=MK \\
& \left( MEF \right)\cap \left( ACD \right)=HK \\
\end{align} \right.$.
Do đó tam giác $MHK$ là thiết diện của tứ diện cắt bởi $\left( MEF \right)$.
Dễ thấy $H,K$ lần lượt là trọng tâm của các tam giác $ABE$ và $ABF$.
Ta có: $AH=AK=HK=\dfrac{2a}{3}$.
Xét hai tam giác $AMH$ và $AMK$ có $AM$ chung, $\widehat{MAH}=\widehat{MAK}={{60}^{0}},\,AH=AK=\dfrac{2a}{3}$ nên hai tam giác này bằng nhau. Suy ra $MH=MK$. Vậy tam giác $MHK$ cân tại $M$.
Áp dụng định lí cosin trong tam giác $AMH$:
$M{{H}^{2}}=A{{M}^{2}}+A{{H}^{2}}-2AMAH.\cos {{60}^{0}}={{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{2a}{3} \right)}^{2}}-\dfrac{{{a}^{2}}}{3}=\dfrac{13{{a}^{2}}}{36}\Rightarrow MH=\dfrac{a\sqrt{13}}{6}$.
Gọi $I$ là trung điểm của đoạn $HK$. Ta có $MI\bot HK$.
Suy ra: $M{{I}^{2}}=M{{H}^{2}}-H{{I}^{2}}=\dfrac{13{{a}^{2}}}{36}-\dfrac{{{a}^{2}}}{9}=\dfrac{{{a}^{2}}}{4}\Rightarrow MI=\dfrac{a}{2}$.
Diện tích thiết diện $MHK$ là: $S=\dfrac{1}{2}MI.HK=\dfrac{1}{2}.\dfrac{2a}{3}.\dfrac{a}{2}=\dfrac{{{a}^{2}}}{6}$.
Câu 43
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, AD, S[C]. Gọi Q là giao điểm của SD với $\left( MNP \right)$ . Tính $\dfrac{SQ}{SD}\,\,?$
[A]. $\dfrac{1}{3}$.
[B]. $\dfrac{1}{4}$.
[C]. $\dfrac{3}{4}$.
[D]. $\dfrac{2}{3}$.
Đáp án C.
Trong mặt phẳng $\left( ABCD \right)$, gọi $E$ là giao điểm của $MN$ với $DC$ và $F$ là trung điểm của $CD$.Dễ thấy $Q$ chính là giao điểm của $PE$ với $SD$.
Ta có: $ME=BC.$ Áp dụng Thales ta có: $\dfrac{ND}{MF}=\dfrac{ED}{EF}=\dfrac{1}{2}\Rightarrow EF=\dfrac{1}{2}EF$.
Suy ra $D$ là trung điểm $EF$.
$PQ$ là đường trung bình của tam giác $EPF$ ta có: $\dfrac{DQ}{PF}=\dfrac{1}{2}$.
$PF$ là đường trung bình của tam giác $CSD$ ta có: $\dfrac{DS}{PF}=2$.
Từ đó suy ra: $\dfrac{SD}{DQ}=4\Rightarrow \dfrac{SQ}{SD}=\dfrac{3}{4}$.
Câu 44
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm O. Gọi M, N , P lần lượt là trung điểm của AB, AD và SO. Gọi H là giao điểm của SC với $\left( MNP \right)$ . Tính $\dfrac{SH}{SC}\,\,?$
[A]. $\dfrac{1}{3}$.
[B]. $\dfrac{1}{4}$.
[C]. $\dfrac{3}{4}$.
[D]. $\dfrac{2}{3}$.
Đáp án B.
Trong mặt phẳng $\left( ABCD \right)$, gọi $I$ là giao điểm của $MN$ với $AO$.
Dễ thấy $H$ chính là giao điểm của $PO$ với $SC$.
Do $MN$ là đường trung bình của tam giác $ABD$ nên $I$ là trung điểm $AO$. Suy ra $\dfrac{AI}{AC}=\dfrac{1}{4}$ và $PI$ là đường trung bình của tam giác $OSA$. Do đó: $IH//SA$.
Áp dụng định lí Thales ta có: $\dfrac{SH}{SD}=\dfrac{AI}{AC}=\dfrac{1}{4}$.
Câu 45
Cho hình chóp $SABCD$ có đáy $ABCD$ là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và C[D]. Trên đường thẳng DS lấy điểm P sao cho D là trung điểm của SP. Gọi R là giao điểm của SB với mặt phẳng $\left( MNP \right)$ . Tính $\dfrac{SR}{SB}\,\,?$
[A]. $\dfrac{1}{3}$.
[B]. $\dfrac{1}{4}$.
[C]. $\dfrac{3}{4}$.
[D]. $\dfrac{2}{5}$.
Đáp án D.
Trong mặt phẳng $\left( ABCD \right)$, gọi $I=BD\cap MN,\,O=AC\cap BD$.
Dễ thấy $R$ chính là giao điểm của $IP$ với $SB$.
Do $MN$ là đường trung bình của tam giác $ABD$ nên $I$ là trung điểm $DO$. Suy ra $\dfrac{DI}{IB}=\dfrac{1}{3}$.
Áp dụng định lí Menelaus vào tam giác $SBD$ ta có:
$\dfrac{BR}{RS}.\dfrac{PS}{PD}.\dfrac{BI}{ID}=1\Rightarrow \dfrac{BR}{RS}.2.\dfrac{1}{3}=1\Rightarrow \dfrac{BR}{RS}=\dfrac{3}{2}\Rightarrow \dfrac{SR}{SB}=\dfrac{2}{5}$