Phép vị tự: các dạng bài cơ bản, trắc nghiệm toán 11
Câu 1
Mệnh đề nào sau đây sai về phép vị tự:
[A]. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
[B]. Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
[C]. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
[D]. Biến đường tròn thành đường tròn cùng bán kính.
Đáp án D.
Câu 2
Cho hai đường thẳng song song $d$ và ${d}’$. Có bao nhiêu phép vị tự đối với tỉ số $k=20$ biến đường thẳng $d$ thành ${d}’$?
[A]. Không có phép nào.
[B]. Có một phép duy nhất.
[C]. Chỉ có 2 phép.
[D]. Có vô số phép.
Đáp án D.
Câu 3
Cho hai đường thẳng cắt nhau $d$ và ${d}’$. Có bao nhiêu phép vị tự biến đường thẳng $d$ thành ${d}’$?
[A]. Không có phép nào.
[B]. Có một phép duy nhất.
[C]. Chỉ có 2 phép.
[D]. Có vô số phép.
Đáp án A
Theo tính chất phépv ị tự biến đường thẳng thành đường thẳng song song hoặc trùng nhay, không có trường hợp $d$ cắt ${d}’$.
Câu 4
Cho hai đường thẳng song song $d$ và ${d}’$, và một điểm $O$ không nằm trên chúng. Có bao nhiêu phép vị tự tâm $O$ biến đường thẳng $d$ thành ${d}’$?
[A]. $0$ .
[B]. $1$ .
[C]. $2$ .
[D]. Vô số.
Đáp án B.
Câu 5
Cho hai đường tròn bằng nhau $\left( O;R \right)$ và $\left( {O}’;R \right)$ với tâm $O$ và tâm ${O}’$ phân biệt. Có bao nhiêu phép vị tự biến $\left( O;R \right)$ thành $\left( {O}’;R \right)$?
[A]. $0$ .
[B]. $1$ .
[C]. $2$ .
[D]. Vô số.
Đáp án B.
Câu 6
Cho hai phép vị tự ${{V}_{\left( O,k \right)}}$ và ${{V}_{\left( {O}’,{k}’ \right)}}$ với $O$ và ${O}’$ là hai điểm phân biệt và $k.{k}’=1$. Hợp của hai phép vị tự đó là phép nào sau đây?
[A]. Phép tịnh tiến.
[B]. Phép đối xứng trục.
[C]. Phép đối xứng tâm.
[D]. Phép quay.
Đáp án A
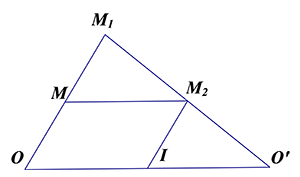
Lấy điểm $M$ bất kỳ: ${{V}_{\left( O;k \right)}}\left( M \right)={{M}_{1}}$ và ${{V}_{\left( {O}’;{k}’ \right)}}\left( {{M}_{1}} \right)={{M}_{2}}\Rightarrow \overrightarrow{O{{M}_{1}}}=k\overrightarrow{OM}$ và $\overrightarrow{{O}'{{M}_{2}}}={k}’\overrightarrow{{O}'{{M}_{1}}}$
Khi đó phép hợp thành $F\left( M \right)={{M}_{2}}.$ Gọi $I$ là ảnh của $O$ qua phép hợp ${{V}_{\left( {O}’;k \right)}}\Rightarrow \overrightarrow{{O}’I}=k\overrightarrow{{O}’O}$
Khi đó $\overrightarrow{I{{M}_{2}}}={k}’\overrightarrow{O{{M}_{1}}}=k.{k}’\overrightarrow{OM}$ nên: $\overrightarrow{M{{M}_{2}}}=\overrightarrow{OI}=\overrightarrow{O{O}’}+\overrightarrow{{O}’I}=\left( 1-{k}’ \right)\overrightarrow{O{O}’}$
Vậy $F$ là phép tịnh tiến theo vectơ $\overrightarrow{u}=\left( 1-{k}’ \right)\overrightarrow{O{O}’}$.
Câu 7
Cho $\Delta ABC$ vuông tại $A$, $AB=6,AC=8$. Phép vị tự tâm $A$ tỉ số $\dfrac{3}{2}$ biến $B$ thành ${B}’$, biến $C$ thành ${C}’$. Mệnh đề nào sau đây sai?
[A]. $B{B}'{C}’C$ là hình thang.
[B]. ${B}'{C}’=12$.
[C]. ${{S}_{{A}'{B}'{C}’}}=\dfrac{3}{4}$.
[D]. Chu vi $\Delta ABC=\dfrac{2}{3}$chu vi $\Delta {A}'{B}'{C}’$.
Đáp án B
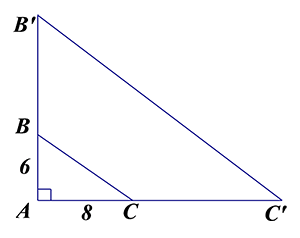
${{V}_{\left( A;\dfrac{3}{2} \right)}}\left( B \right)=\left( {{B}’} \right)\Rightarrow A{B}’=\dfrac{3}{2}AB=9;{{V}_{\left( A;\dfrac{3}{2} \right)}}\left( C \right)=\left( {{C}’} \right)\Rightarrow A{C}’=\dfrac{3}{2}AC=12\Rightarrow {B}'{C}’=\sqrt{{{9}^{2}}+{{12}^{2}}}=15$.
Câu 8
Cho hình thang $ABCD\,\,\left( AB//CD \right)$. Đáy lớn $AB=8$, đáy nhỏ $CD=4$. Gọi $I$ là giao điểm của hai đường chéo và $J$ là giao điểm của hai cạnh bên. Phép biến hình $\overrightarrow{AB}$ thành $\overrightarrow{CD}$ là phép vị tự nào?
[A]. ${{V}_{\left( I,\dfrac{1}{2} \right)}}$ .
[B]. ${{V}_{\left( J,\dfrac{1}{2} \right)}}$ .
[C]. ${{V}_{\left( I,-\dfrac{1}{2} \right)}}$ .
[D]. ${{V}_{\left( J,-\dfrac{1}{2} \right)}}$.
Đáp án C
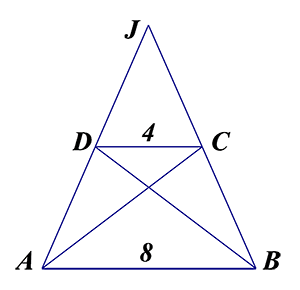
Ta có
\[\begin{align}
& \dfrac{AB}{CD}=\dfrac{1}{2};{{V}_{\left( I,\dfrac{1}{2} \right)}}\left( A \right)=C\Leftrightarrow \overrightarrow{IC}=-\dfrac{1}{2}\overrightarrow{IA};{{V}_{\left( I,\dfrac{1}{2} \right)}}\left( B \right)=D\Leftrightarrow \overrightarrow{ID}=-\dfrac{1}{2}\overrightarrow{IB} \\
& \Rightarrow \overrightarrow{IC}-\overrightarrow{ID}=-\dfrac{1}{2}\left( \overrightarrow{IA}-\overrightarrow{IB} \right)\Leftrightarrow \overrightarrow{CD}=-\dfrac{1}{2}\overrightarrow{AB} \\
\end{align}\].
Câu 9
Cho đường tròn $\left( O;R \right)$ và một điểm $A$ cố định trên đường tròn. $BC$ là dây cung di động và $BC$ có độ dài không đổi bằng $2a$ $\left( a<R \right)$. Gọi $M$ là trung điểm $BC$. Khi đó tập hợp trọng tâm $G$ của $\Delta ABC$ là:
[A]. $G={{V}_{\left( A,\dfrac{2}{3} \right)}}\left( M \right)$, tập hợp là một đường tròn.
[B]. $G={{V}_{\left( O,\dfrac{1}{2} \right)}}\left( M \right)$, tập hợp là một đường thẳng.
[C]. $G={{V}_{\left( A,\dfrac{1}{3} \right)}}\left( M \right)$, tập hợp là một đường tròn.
[D]. $G={{V}_{\left( B,\dfrac{2}{3} \right)}}\left( M \right)$, tập hợp là một đường thẳng.
Đáp án A
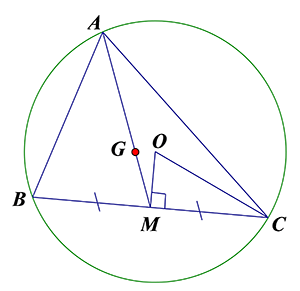
Ta có: $OM\bot BC\Rightarrow OM=\sqrt{{{R}^{2}}-{{a}^{2}}}\Rightarrow M\in \left( O;\sqrt{{{R}^{2}}-{{a}^{2}}} \right)$
Ta có: $\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\Rightarrow G={{V}_{\left( A,\dfrac{2}{3} \right)}}\left( M \right)$
Khi $M$ di động trên đường tròn $\left( O;\sqrt{{{R}^{2}}-{{a}^{2}}} \right)$ thì $G$ chạy trên đường tròn $\left( {{O}’} \right)$ là ảnh của đường tròn $\left( O \right)$ qua phép vị tự ${{V}_{\left( A,\dfrac{2}{3} \right)}}$.
Câu 10
Cho đường tròn $\left( O;R \right)$ đường kính $AB$. Một đường tròn $\left( {{O}’} \right)$ tiếp xúc với đường tròn $\left( O \right)$ và đoạn $AB$lần lượt tại $C$ và $D$ . Đường thẳng $CD$ cắt $\left( O;R \right)$ tại $I$. Tính độ dài đoạn $AI$ .
[A]. $2R\sqrt{3}$ .
[B]. $R\sqrt{2}$ .
[C]. $R\sqrt{3}$ .
[D]. $2R\sqrt{2}$.
Đáp án B
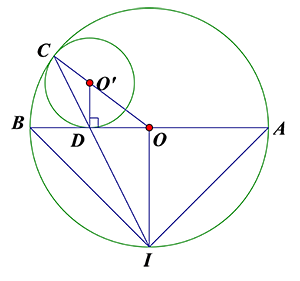
Ta có: ${{V}_{\left( C,\dfrac{{{R}’}}{R} \right)}}\left( O \right)={O}’\Leftrightarrow C{O}’=\dfrac{{{R}’}}{R}CO\text{ }\left( 1 \right)$
${{V}_{\left( C,\dfrac{{{R}’}}{R} \right)}}\left( I \right)=D\Leftrightarrow CD=\dfrac{{{R}’}}{R}CI\text{ }\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)\Rightarrow$$\dfrac{CD’}{CD}=\dfrac{CO}{CI}\Rightarrow OI//{O}’D\Rightarrow OI\bot AB\Rightarrow I$ là điểm chính giữa của cung $AB$.
Câu 11
Cho hai đường tròn $\left( O;R \right)$ và $\left( {O}’;{R}’ \right)$ tiếp xúc trong tại $A$ $\left( R>{R}’ \right)$. Đường kính qua $A$ cắt $\left( O;R \right)$ tại $B$ và cắt $\left( {O}’;{R}’ \right)$ tại $C$. Một đường thẳng di động qua $A$ cắt $\left( O;R \right)$ tại $M$ và cắt $\left( {O}’;{R}’ \right)$ tại $N$. Gọi $I$ là giao điểm của $BN$ và $CM$. Mệnh đề nào sau đây là đúng?
[A]. Tập hợp điểm $I$ là đường tròn: $\left( {{{O}’}’} \right)={{V}_{\left( C,\dfrac{{{R}’}}{R+{R}’} \right)}}\left( \left( O,R \right) \right)$.
[B]. Tập hợp điểm $I$ là đường tròn: $\left( {{{O}’}’} \right)={{V}_{\left( C,\dfrac{R}{R+{R}’} \right)}}\left( \left( O,R \right) \right)$.
[C]. Tập hợp điểm $I$ là đường tròn: $\left( {{{O}’}’} \right)={{V}_{\left( M,\dfrac{{{R}’}}{R+{R}’} \right)}}\left( \left( O,R \right) \right)$.
[D]. Tập hợp điểm $I$ là đường tròn: $\left( {{{O}’}’} \right)={{V}_{\left( M,\dfrac{R}{R+{R}’} \right)}}\left( \left( O,R \right) \right)$.
Đáp án A
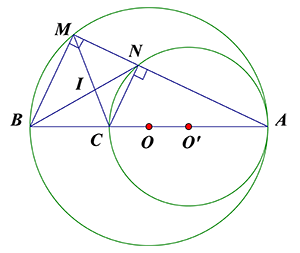
Ta dự đoán ${{V}_{\left( C;\dfrac{CI}{CM} \right)}}\left( M \right)=I$ mà $M$ nắm trên đường tròn $\left( O \right)\Rightarrow I$ nằm trên đường tròn
$\left( {{O}_{1}} \right)={{V}_{\left( C;\dfrac{CI}{CM} \right)}}\left( O \right)$
Ta cần chứng minh $\dfrac{CI}{CM}$ theo $R$ và ${R}’$
Ta có $\dfrac{CM}{CI}=\dfrac{CI+IM}{CI}=1+\dfrac{IM}{CI}$ mà $\dfrac{IM}{CI}=\dfrac{IB}{IN}=\dfrac{BM}{CN}=\dfrac{AB}{AC}=\dfrac{R}{{{R}’}}\Rightarrow \dfrac{CI}{CM}=\dfrac{{{R}’}}{R+{R}’}$
$\Rightarrow {{V}_{\left( C,\dfrac{{R}’\,}{R+{R}’\,} \right)}}\left( M \right)=I$