Phép quay: dạng bài tập cơ bản, trắc nghiệm toán 11
Câu 1
Cho 2 đường thẳng bất kì \[d\] và \[d\]. Có bao nhiêu phép quay biến đường thẳng \[d\] thành đường thẳng \[d\]?
[A]. không có phép nào.
[B]. có 1 phép duy nhất.
[C]. chỉ có 2 phép.
[D]. có vô phép số.
Đáp án D.
Câu 2
Cho hình vuông tâm \[O\]. Hỏi có bao nhiêu phép quay tâm \[O\] góc $\alpha $, $0\le \alpha <2\pi $ biến hình vuông thành chính nó ?
[A]. \[1\] .
[B]. \[2\] .
[C]. \[3\] .
[D]. \[4.\]
Đáp án D.
Thật vậy, các phép quay biến hình vuông thành chính nó: \[{{Q}_{\left( O,{{0}^{0}} \right)}},\,{{Q}_{\left( O,{{90}^{0}} \right)}},\,{{Q}_{\left( O,{{180}^{0}} \right)}},\,{{Q}_{\left( O,{{270}^{0}} \right)}}.\]
Câu 3
Gọi $d$ là hình ảnh của $d$ qua tâm $I$ góc quay $\varphi $ (biết $I$ không nằm trên $d$), đường thẳng $d$ song với $d$ khi:
[A]. $\varphi =\dfrac{\pi }{3}$ .
[B]. $\varphi =\dfrac{\pi }{6}$.
[C]. $\varphi =\dfrac{2\pi }{3}$.
[D]. $\varphi =-\pi $.
Đáp án D.
Khi \[\varphi =-\pi \], phép quay trở thành phép đối xứng tâm I \[\Rightarrow d//{d}’\].
Câu 4
Cho hai đường tròn cùng bán kính $\left( O \right)$ và $\left( O’ \right)$ tiếp xúc ngoài nhau. Có bao nhiêu phép quay góc $90{}^\circ $ biến hình tròn $\left( O \right)$ thành $\left( O’ \right)$?
[A]. \[0\] .
[B]. \[1\] .
[C]. \[2\] .
[D]. Vô số.
Đáp án B.
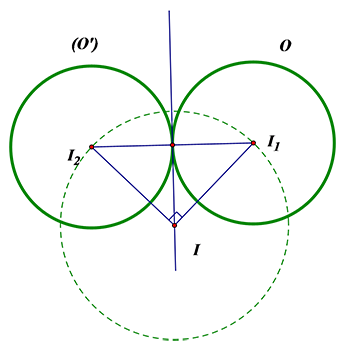
Gọi $I$ là tâm của phép quay, \[{{I}_{1}},\,{{I}_{2}}\] là tâm các đường tròn \[\left( O \right)\] và \[\left( {{O}’} \right)\].
\[{{Q}_{\left( I,{{90}^{0}} \right)}}\left( {{I}_{1}} \right)={{I}_{2}}\Leftrightarrow \left\{ \begin{align}
& I{{I}_{1}}=I{{I}_{2}} \\
& \left( I{{I}_{1}},I{{I}_{2}} \right)={{90}^{0}} \\
\end{align} \right.\]. Vậy chỉ có 1 phép quay thỏa mãn.
Câu 5
Cho hình lục giác đều \[ABCDE\] tâm\[O\] . Tìm ảnh của tam giác \[AOF\] qua phép quay tâm \[O\] góc quay ${{120}^{0}}$.
[A]. $\Delta OAB$.
[B]. $\Delta BOC$.
[C]. $\Delta DOC$.
[D]. $\Delta EOD$.
Đáp án D.
\[{{Q}_{\left( O,{{120}^{0}} \right)}}\left( A \right)=E\], \[{{Q}_{\left( O,{{120}^{0}} \right)}}\left( F \right)=D\], \[{{Q}_{\left( O,{{120}^{0}} \right)}}\left( O \right)=O\Rightarrow {{Q}_{\left( O,{{120}^{0}} \right)}}\left( \Delta AOF \right)=\Delta EOD\].
Câu 6
Chọn \[12\] giờ làm mốc, khi đồng hồ chỉ năm giờ đúng thì kim giờ đã quay được một góc bao nhiêu độ ?
[A]. ${{270}^{0}}$.
[B]. $-{{360}^{0}}$.
[C]. $-{{150}^{0}}$.
[D]. ${{135}^{0}}$.
Đáp án C.
Khi kim giờ chỉ đến năm giờ đúng thì kim giờ quay được đúng \[-{{150}^{0}}\] tức theo chiều âm.
Câu 7
Cho hai đường thẳng ${{\Delta }_{1}}$ và ${{\Delta }_{2}}$ biết ${{Q}_{\left( O;-{{120}^{0}} \right)}}\left( {{\Delta }_{1}} \right)={{\Delta }_{2}}$. Mệnh đề nào sau đây đúng ?
A$\left( {{\Delta }_{1}},{{\Delta }_{2}} \right)={{120}^{0}}$ .
[B]. ${{\Delta }_{1}}$//${{\Delta }_{2}}$ .
[C]. $\left( {{\Delta }_{1}},{{\Delta }_{2}} \right)=-{{120}^{0}}$.
[D]. $\left( {{\Delta }_{1}},{{\Delta }_{2}} \right)={{60}^{0}}$.
Đáp án D.
Vì góc quay 1200 nên góc giữa hai đường thẳng là: 1800 – 1200 = 600
Câu 8
Cho hai điểm phân biệt \[A,B\] và ${{Q}_{\left( A;{{30}^{0}} \right)}}\left( B \right)=C$. Mệnh đề nào sau đây đúng ?
[A]. $ABC={{30}^{0}}$ .
[B]. $ABC={{90}^{0}}$.
[C]. $ABC={{45}^{0}}$.
[D]. $ABC={{75}^{0}}$.
Đáp án D.
Câu 9
Cho hai điểm phân biệt \[I,M\] và ${{Q}_{\left( I;-32\pi \right)}}\left( M \right)=N$. Mệnh đề nào sau đây đúng ?
[A]. \[M\] là trung điểm của đoạn \[IN\].
[B]. \[N\] là trung điểm của đoạn \[IM\].
[C]. \[I\] là trung điểm của đoạn \[MN\].
[D]. $M\equiv N$.
Đáp án D.
Câu 10
Cho $\Delta ABC$ đều (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây sai ?
[A]. ${{Q}_{\left( A,\dfrac{\pi }{3} \right)}}\left( B \right)=C$ .
[B]. ${{Q}_{\left( A,-\dfrac{\pi }{3} \right)}}\left( C \right)=B$.
[C]. ${{Q}_{\left( A,\dfrac{7\pi }{3} \right)}}\left( C \right)=B$.
[D]. ${{Q}_{\left( A,-\dfrac{7\pi }{3} \right)}}\left( A \right)=C$.
Đáp án C.
Câu 11
Gọi $I$ là tâm hình vuông \[ABCD\] (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây sai ?
[A]. ${{Q}_{\left( I,{{90}^{0}} \right)}}\left( \Delta IBC \right)=\Delta ICD$.
[B]. ${{Q}_{\left( I,-{{90}^{0}} \right)}}\left( \Delta IBC \right)=\Delta IAB$.
[C]. ${{Q}_{\left( I,{{180}^{0}} \right)}}\left( \Delta IBC \right)=\Delta IDA$.
[D]. ${{Q}_{\left( I,{{360}^{0}} \right)}}\left( \Delta IBC \right)=\Delta IDA$.
Đáp án D.
Câu 12
Gọi $I$ là tâm ngũ giác đều \[ABCDE\] (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai ?
[A]. ${{Q}_{\left( I,{{144}^{0}} \right)}}\left( CD \right)=EA$.
[B]. ${{Q}_{\left( I,{{72}^{0}} \right)}}\left( AB \right)=BC$.
[C]. ${{Q}_{\left( I,{{144}^{0}} \right)}}\left( AB \right)=DE$.
[D]. ${{Q}_{\left( I,{{72}^{0}} \right)}}\left( CD \right)=BC$.
Đáp án C.
Câu 13
Gọi $I$ là tâm lục giác đều \[ABCDEF\] (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai ?
[A]. ${{Q}_{\left( I,-{{120}^{0}} \right)}}\left( \Delta IED \right)=\Delta IBA$.
[B]. ${{Q}_{\left( I,-{{60}^{0}} \right)}}\left( \Delta IAB \right)=\Delta IBC$.
[C]. ${{Q}_{\left( I,{{60}^{0}} \right)}}\left( AB \right)=BC$.
[D]. ${{Q}_{\left( I,{{180}^{0}} \right)}}\left( \Delta ICD \right)=\Delta IFA$.
Đáp án B.
Câu 14
Cho hai tam giác vuông cân \[OAB\] và \[OAB\] có chung đỉnh \[O\] sao cho \[O\] nằm trên đoạn \[AB\] và nằm ngoài đoạn thẳng \[AB\] . Gọi \[G\] và \[G\] lần lượt là trọng tâm các tam giác \[OAA\] và \[OBB\]. Xác định dạng của tam giác \[GOG\]
[A]. cân.
[B]. vuông.
[C]. vuông cân.
[D]. đều.
Đáp án C.
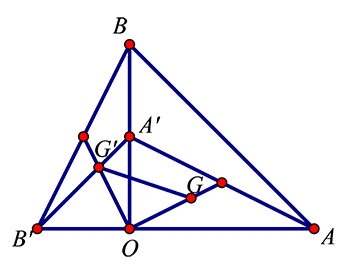
\[\left\{ \begin{align}
& {{Q}_{\left( O,{{90}^{0}} \right)}}\left( A \right)=B \\
& {{Q}_{\left( O,{{90}^{0}} \right)}}\left( {{A}’} \right)={B}’ \\
\end{align} \right.\]\[\Rightarrow {{Q}_{\left( O,{{90}^{0}} \right)}}\left( \Delta OA{A}’ \right)=\Delta OB{B}’\Rightarrow {{Q}_{\left( O,{{90}^{0}} \right)}}\left( G \right)={G}’\]. Do đó \[OG=O{G}’\] và \[\widehat{GO{G}’}={{90}^{0}}\]
Câu 15
Cho 3 điểm $A$, $B$, $C$, điểm \[B\] nằm giữa \[A\] và \[C\] . Dựng về phía đường thẳng \[AC\] các tam giác đều \[ABE\] và \[BCF\] . Gọi \[M\] và \[N\] lần lượt là trung điểm của \[AF\] và \[EC\] . Xác định dạng của $\Delta BMN$.
[A]. cân.
[B]. vuông.
[C]. vuông cân.
[D]. đều.
Do đó \[OG=O{G}’\] và \[\widehat{GO{G}’}={{90}^{0}}\]
Đáp án D.
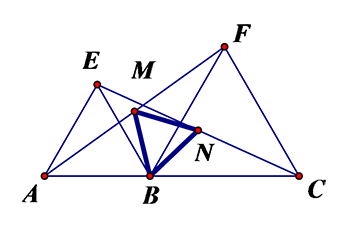
Phép quay tâm $B$ góc quay ${{60}^{0}}$ biến các điểm $E,\,C$ lần lượt thành $A,\,F$ biến đoạn $EC$ thành $AF$ nên biến trung điểm $N$ của $EC$ thành trung điểm $M$ của \[AF\Rightarrow BN=BM\] và \[\left( BN,BM \right)={{60}^{0}}\Rightarrow \Delta BMN\] đều.
Câu 16
Cho đường thẳng $d$ và điểm $O$ cố định không thuộc $d$. $M$ là điểm di động trên $d$. Xác định quỹ tích điểm $N$ sao cho $\Delta OMN$ đều.
[A]. $N\in {d}’$ với ${d}’={{Q}_{\left( O,60{}^\circ \right)}}\left( d \right)$.
[B]. $N\in {d}’$ với ${d}’={{Q}_{\left( O,180{}^\circ \right)}}\left( d \right)$.
[C]. $N\in {d}’$ với ${d}’={{Q}_{\left( O,120{}^\circ \right)}}\left( d \right)$.
[D]. $N\in {d}’$ với ${d}’={{Q}_{\left( O,-120{}^\circ \right)}}\left( d \right)$.
Đáp án [A].
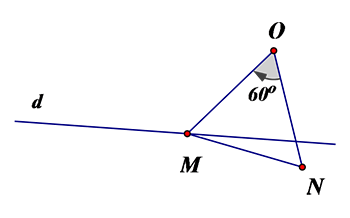
Vì $\Delta OMN$ đều và $O$ cố định \[\Rightarrow N={{Q}_{\left( O,{{60}^{0}} \right)}}\left( M \right)\].
Câu 17
Cho hình vuông \[ABCD\], $M\in BC$, $K\in DC$ sao cho $\widehat{BAM}=\widehat{MAK}$. Khi đó mệnh đề nào sau đây là đúng ?
[A]. $AD=AK-KD$ .
[B]. $AB=AM+DK$.
[C]. $AK=BM+KD$.
[D]. $AM=BM+AB$.
Đáp án C.
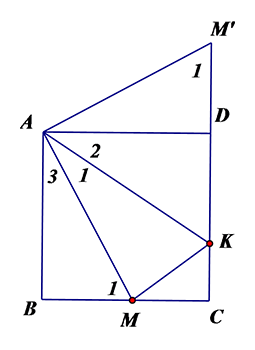
Ta có: \[{{Q}_{\left( A,{{90}^{0}} \right)}}:\,B\to D;\,{{Q}_{\left( A,{{90}^{0}} \right)}}:\,M\to {M}’\Rightarrow {{Q}_{\left( A,{{90}^{0}} \right)}}:\,BM\to D{M}’\Rightarrow BM=D{M}’\].
Vậy, \[BM+KD=D{M}’+KD\].
Cần chứng minh: \[{M}’,\,D,\,K\] thẳng hàng và \[\Delta AK{M}’\] cân tại $K$\[\Rightarrow D{M}’+KD=K{M}’\].
Thật vậy: \[{{Q}_{\left( A,{{90}^{0}} \right)}}\left( BM \right)=D{M}’\Rightarrow BM\bot D{M}’\]. Mà \[BM\text{ // }AD\Rightarrow AD\bot D{M}’\Rightarrow \widehat{AD{M}’}={{90}^{0}}\]
\[{M}’,\,D,\,K\] thẳng hàng.
Ta có: \[{{Q}_{\left( A,{{90}^{0}} \right)}}:\,\Delta ABM\to \,\Delta AD{M}’\Rightarrow \widehat{{{M}_{1}}}=\widehat{{{M}_{1}}^{\prime }}\].
Có: \[\widehat{{M}’AK}+\widehat{{{A}_{1}}}={{90}^{0}}\Rightarrow \widehat{{M}’AK}+\widehat{{{A}_{3}}}={{90}^{0}}\] (do \[\widehat{{{A}_{1}}}=\widehat{{{A}_{3}}}\]) \[\Rightarrow \widehat{{M}’AK}=\widehat{{{M}_{1}}}\Rightarrow \Delta AKM\] cân tại $K$
\[\Rightarrow K{M}’=KD+D{M}’=KA\Rightarrow KD+BM=AK\]
Câu 18
Cho $\Delta ABC$. Dựng về phía ngoài tam giác các hình vuông \[BCIJ\],\[ACMN\]. Gọi \[O,P\] lần lượt là tâm đối xứng của chúng, \[D\] là trung điểm của \[AB\]. Xác định dạng của $\Delta DOP$.
[A]. cân .
[B]. vuông.
[C]. vuông cân.
[D]. đều.
Đáp án C.
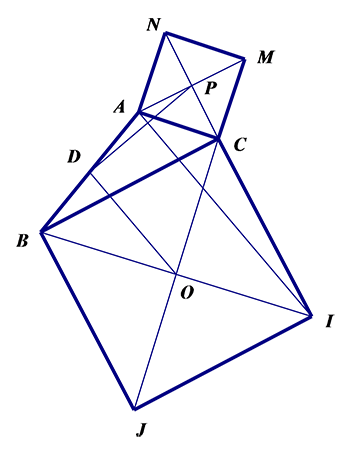
Ta có: \[{{Q}_{\left( C,{{90}^{0}} \right)}}:\,M\to A;\,B\to I\Rightarrow {{Q}_{\left( O,{{90}^{0}} \right)}}:\,MB\to AI\Rightarrow MB=AI\].
Mà \[\left\{ \begin{align}
& DP\text{ // }BM,\,DP=\dfrac{1}{2}BM \\
& DO\text{ // }AI,\,DO=\dfrac{1}{2}AI\, \\
\end{align} \right.\]\[\Rightarrow DO=DP\] và \[DO\bot DP\]
\[\Rightarrow \Delta DOP\] là tam giác vuông cân.