Phép tịnh tiến: xác định ảnh của một điểm hoặc một hình bằng phương pháp tọa độ, trắc nghiệm toán 11
Câu 1
Trong mặt phẳng tọa độ\[Oxy\], tìm tọa độ điểm ${M}’$ là ảnh của điểm $M\left( 1;2 \right)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=\left( 3;1 \right).$
[A]. ${M}’\left( 4;-2 \right)$ .
[B]. ${M}’\left( 4;2 \right)$.
[C]. ${M}’\left( 2;1 \right)$.
[D]. ${M}’\left( 4;-1 \right)$.
Đáp án B.
${{T}_{\overrightarrow{v}}}\left( M \right)={M}’\left( {x}’;{y}’ \right)\Leftrightarrow \left\{ \begin{align}
& {x}’=4 \\
& {y}’=2 \\
\end{align} \right.\Rightarrow {M}’\left( 4;2 \right)$
Câu 2
Trong mặt phẳng tọa độ \[Oxy\], cho vectơ $\overrightarrow{v}=\left( 2;1 \right)$và điểm $A\left( 4;5 \right).$ Hỏi $A$ là ảnh của điểm nào sau đây qua phép tịnh tiến theo vectơ $\overrightarrow{v}.$
[A]. $\left( 1;6 \right)$ .
[B]. $\left( 2;4 \right)$.
[C]. $\left( 4;7 \right)$.
[D]. $\left( 6;6 \right)$.
Đáp án B.
Theo biểu thức tọa độ $\Rightarrow \left\{ \begin{align}
& {{x}_{A}}=x+{{x}_{{\vec{v}}}} \\
& {{y}_{A}}=y+{{y}_{{\vec{v}}}} \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x=2 \\
& y=4 \\
\end{align} \right.$
Câu 3
Trong mặt phẳng tọa độ \[Oxy\], cho điểm $A\left( 2;2 \right)$, $B\left( 4;6 \right)$ và ${{T}_{\overrightarrow{v}}}\left( A \right)=B$ . Tìm vectơ $\overrightarrow{v}.$
[A]. $\left( 1;2 \right)$ .
[B]. $\left( 2;4 \right)$.
[C]. $\left( 4;2 \right)$.
[D]. $\left( -2;-4 \right)$.
Đáp án B.
Ta có $\left\{ \begin{align}
& {{x}_{\overrightarrow{v}}}={{x}_{B}}-{{x}_{A}} \\
& {{y}_{\overrightarrow{v}}}={{y}_{B}}-{{y}_{A}} \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& {{x}_{\overrightarrow{v}}}=2 \\
& {{y}_{\overrightarrow{v}}}=4 \\
\end{align} \right.$
Câu 4
Trong mặt phẳng tọa độ\[Oxy\], biết điểm ${M}’\left( -3;0 \right)$ là ảnh của điểm $M\left( 1;-2 \right)$ qua ${{T}_{\overrightarrow{u}}}$ và điểm ${{M}’}’\left( 2;3 \right)$ là ảnh của ${M}’$ qua ${{T}_{\overrightarrow{v}}}$. Tìm tọa độ vectơ $\overrightarrow{u}+\overrightarrow{v}.$
[A]. $\left( 1;5 \right)$ .
[B]. $\left( -2;-2 \right)$.
[C]. $\left( 1;-1 \right)$.
[D]. $\left( -1;5 \right)$.
Đáp án A.
Ta có $\overrightarrow{u}=\overrightarrow{M{M}’},\,\,\overrightarrow{v}=\overrightarrow{{M}'{{M}’}’}$ $\Rightarrow \overrightarrow{u}+\overrightarrow{v}=\overrightarrow{M{{M}’}’}=\left( 1;5 \right)$.
Câu 5
Trong mặt phẳng tọa độ\[Oxy\], cho các điểm ${A}’,\,{B}’$ lần lượt là ảnh của các điểm $A\left( 2;3 \right),\,B\left( 1;1 \right)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=\left( 3;1 \right)$. Tính độ dài vectơ$\overrightarrow{{A}'{B}’}.$
[A]. $2$.
[B]. $\sqrt{3}$.
[C]. $\sqrt{5}$.
[D]. $\sqrt{2}$.
Đáp án C.
Ta có $\begin{matrix}
{{T}_{\overrightarrow{v}}}\left( A \right)={A}’ \\
{{T}_{\overrightarrow{v}}}\left( B \right)={B}’ \\
\end{matrix}\Rightarrow {A}'{B}’=AB=\sqrt{5}$ .
Câu 6
Trong mặt phẳng tọa độ \[Oxy\], cho tam giác $ABC$ có các điểm $A\left( 3;0 \right),\,B\left( -2;4 \right),\,C\left( -4;5 \right)$ . $G$ là trọng tâm tam giác $ABC$ và phép tịnh tiến theo vectơ $\overrightarrow{u}\ne \overrightarrow{0}$ biến điểm $A$ thành $G$ . Tìm tọa độ ${G}’$ biết ${G}’={{T}_{\overrightarrow{u}}}\left( G \right).$
[A]. ${G}’\left( -5;6 \right)$ .
[B]. ${G}’\left( 5;6 \right)$.
[C]. ${G}’\left( 3;1 \right)$.
[D]. ${G}’\left( -1;3 \right)$.
Đáp án A.
Ta tìm được $G\left( -1;3 \right)\Rightarrow \overrightarrow{u}=\overrightarrow{AG}=\left( -4;3 \right)$
${{T}_{\overrightarrow{AG}}}\left( G \right)={G}’\Rightarrow \overrightarrow{AG}=\overrightarrow{G{G}’}\Rightarrow {G}’\left( -5;6 \right)$ .
Câu 7
Trong mặt phẳng tọa độ\[Oxy\], cho đường thẳng $\Delta :x+5y-1=0$ và vectơ $\overrightarrow{v}=\left( 4;2 \right)$. Khi đó ảnh của đường thẳng $\Delta $ qua phép tịnh tiến theo vectơ $\overrightarrow{v}$ là
[A]. $x+5y-15=0$ .
[B]. $x+5y+15=0$.
[C]. $x+5y+6=0$.
[D]. $-x-5y+7=0$.
Đáp án A.
Ảnh của $\Delta $ có dạng $x+5y+c=0\,\,\left( {{\Delta }’} \right)$
Chọn $A\left( 1;0 \right)\in \Delta :\,\,{{T}_{\overrightarrow{v}}}\left( A \right)={A}’\left( x;y \right)\in {\Delta }’\Rightarrow {A}’\left( 5;2 \right)$ thế vào ${\Delta }’:5+10+c=0\Rightarrow c=-15$
$\Rightarrow {\Delta }’:x+5y-15=0$ .
Câu 8
Trong mặt phẳng tọa độ \[Oxy\], cho $\overrightarrow{v}=\left( -4;2 \right)$ và đường thẳng ${\Delta }’:2x+y-5=0$. Hỏi ${\Delta }’$ là ảnh của đường thẳng $\Delta $ nào sau đây qua ${{T}_{\overrightarrow{v}}}.$
[A]. $\Delta :2x+y+5=0$ .
[B]. $\Delta :2x+y-9=0$.
[C]. $\Delta :2x+y-15=0$.
[D]. $\Delta :2x+y-11=0$.
Đáp án D.
Điểm $M\left( x;y \right)\in \Delta $ biến thành $M\left( {x}’;{y}’ \right)\in {\Delta }’$ $\Rightarrow \left\{ \begin{align}
& {x}’=x-4 \\
& {y}’=y+2 \\
\end{align} \right.$
thay ${x}’,\,{y}’$ vào
${\Delta }’:2x+y-11=0$ .
Câu 9
Trong mặt phẳng tọa độ\[Oxy\], cho đường thẳng $\Delta :\left\{ \begin{align}
& x=1+2t \\
& y=-1-t \\
\end{align} \right.$ và đường thẳng ${\Delta }’:x+2y-1=0$. Tìm tọa độ vectơ $\overrightarrow{v}$ biết ${{T}_{\overrightarrow{v}}}\left( \Delta \right)={\Delta }’.$
[A]. $\vec{v}=\left( 0;-1 \right)$ .
[B]. $\vec{v}=\left( 0;2 \right)$.
[C]. $\vec{v}=\left( 0;1 \right)$.
[D]. $\vec{v}=\left( -1;1 \right)$.
Đáp án C.
Chọn $A\left( 1;-1 \right)\in \Delta $
Thử đáp án C $\Rightarrow {{T}_{\overrightarrow{v}}}\left( A \right)={A}’\Rightarrow {A}’\left( 1;0 \right)\in {\Delta }’$ (thỏa mãn)
Câu 10
Trong mặt phẳng tọa độ \[Oxy\], tìm phương trình đường tròn $\left( {{C}’} \right)$ là ảnh của đường tròn $\left( C \right):{{x}^{2}}+{{y}^{2}}-4x-2y+1=0$ qua phép tịnh tiến theo $\overrightarrow{v}=\left( 1;3 \right).$
[A]. $\left( {{C}’} \right):{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=2$ .
[B]. $\left( {{C}’} \right):{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=4$.
[C]. \[\left( {{C}’} \right):{{\left( x+3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=4\].
[D]. $\left( {{C}’} \right):{{\left( x+3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=4$.
Đáp án B.
Đường tròn $\left( C \right)$ có tâm $I\left( 2;1 \right)$ , bán kính $R=2$
Ta có ${I}’={{T}_{\overrightarrow{v}}}\left( I \right)\Rightarrow {I}’\left( 3;4 \right)\Rightarrow \left( {{C}’} \right):{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=4$ .
Câu 11
Trong mặt phẳng tọa độ \[Oxy\], cho $\overrightarrow{v}=\left( 3;-1 \right)$ và đường tròn $\left( C \right):{{\left( x-4 \right)}^{2}}+{{y}^{2}}=16$ . Ảnh của $\left( C \right)$ qua phép tịnh tiến ${{T}_{\overrightarrow{v}}}$ là
[A]. ${{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=16$ .
[B]. ${{\left( x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=16$.
[C]. ${{\left( x-7 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=16$.
[D]. ${{\left( x+7 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=16$.
Đáp án C.
Đường tròn $\left( C \right)$ có tâm $I\left( 4;0 \right)$ , bán kính $R=4$
Ta có ${{T}_{\overrightarrow{v}}}\left( I \right)={I}’\left( 7;-1 \right)$
Vậy đường tròn ảnh là $\left( {{C}’} \right):{{\left( x-7 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=16$
Câu 12
Trong mặt phẳng tọa độ\[Oxy\], cho $\overrightarrow{v}=\left( 1;-2 \right)$ và đường cong $\left( C \right):2{{x}^{2}}+4{{y}^{2}}=1$ . Ảnh của $\left( C \right)$ qua phép tịn tiến ${{T}_{\overrightarrow{v}}}$ là
[A]. $2{{x}^{2}}+4{{y}^{2}}+4x+16y-17=0$ .
[B]. $2{{x}^{2}}+4{{y}^{2}}-4x+16y+17=0$.
[C]. $2{{x}^{2}}+4{{y}^{2}}-4x-16y+17=0$.
[D]. $2{{x}^{2}}+4{{y}^{2}}-4x-16y-7=0$.
Đáp án B.
Sử dụng quỹ tích điểm $M\left( x;y \right)\in \left( C \right)$ : ${{T}_{\overrightarrow{v}}}\left( M \right)={M}’\left( {x}’;{y}’ \right)\in \left( {{C}’} \right)$ $\Rightarrow \left\{ \begin{align}
& {x}’=x+1 \\
& {y}’=y-2 \\
\end{align} \right.$$\Rightarrow \left\{ \begin{align}
& x={x}’-1 \\
& y={y}’+2 \\
\end{align} \right.$ Thay vào $\left( C \right)$ ta được đáp án B.
Câu 13
Ảnh của $\left( E \right)$ qua phép tịn tiến ${{T}_{\overrightarrow{v}}}$ là:
[A]. \[\left( E \right):\dfrac{{{\left( x-2 \right)}^{2}}}{16}+\dfrac{{{\left( y-1 \right)}^{2}}}{9}=1\] .
[B]. \[\left( E \right):\dfrac{{{\left( x+2 \right)}^{2}}}{16}+\dfrac{{{\left( y+1 \right)}^{2}}}{9}=1\].
[C]. $\left( E \right):\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{9}=1$.
[D]. $\left( E \right):\dfrac{{{x}^{2}}-2}{16}+\dfrac{{{y}^{2}}-1}{9}=1$.
Đáp án A.
Sử dụng quỹ tích điểm : ${{T}_{\overrightarrow{v}}}\left( M \right)={M}’\left( {x}’;{y}’ \right)$ với mọi điểm $M\left( x;y \right)\in \left( E \right)$$\Rightarrow \left\{ \begin{align}
& x={x}’-2 \\
& y={y}’-2 \\
\end{align} \right.$
Thay vào $\left( E \right)$ ta được đáp án A.
Câu 14
Trong mặt phẳng tọa độ\[Oxy\], với $\alpha ,a,b$ là những số cho trước, xét phép biến hình $F$ biến mỗi điểm $M\left( x;y \right)$ thành điểm $M’\left( x’;y’ \right)$ trong đó: $\left\{ \begin{align}
& x’=x.\cos \alpha -y.\sin \alpha +a \\
& y’=x.\sin \alpha +y.cos\alpha +b \\
\end{align} \right.$ .
Cho hai điểm $M\left( {{x}_{1}};{{y}_{1}} \right)$, $N\left( {{x}_{2}};{{y}_{2}} \right)$, gọi $M’,N’$ lần lượt là ảnh của $M,N$ qua phép biến hình $F$. Khi đó khoảng cách $d$ giữa $M’$ và $N’$ bằng:
[A]. $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .
[B]. $d=\sqrt{{{\left( {{x}_{2}}+{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}+{{y}_{1}} \right)}^{2}}}$.
[C]. $d=\sqrt{{{\left( {{x}_{2}}+{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
[D]. $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}+{{y}_{1}} \right)}^{2}}}$.
Đáp án A.
Ta có $\left\{ \begin{align}
& {{x}_{1}}^{\prime }={{x}_{1}}.\cos \,\alpha -{{y}_{1}}.\sin \,\alpha +a \\
& {{y}_{1}}^{\prime }={{x}_{1}}.\sin \,\alpha -{{y}_{1}}.\cos \,\alpha +b \\
\end{align} \right.$
$\left\{ \begin{align}
& {{x}_{2}}^{\prime }={{x}_{2}}.\cos \,\alpha -{{y}_{2}}.\sin \,\alpha +a \\
& {{y}_{2}}^{\prime }={{x}_{2}}.\sin \,\alpha -{{y}_{2}}.\cos \,\alpha +b \\
\end{align} \right.$
$\Rightarrow {M}'{N}’=\sqrt{{{\left( {{x}_{2}}^{\prime }-{{x}_{1}}^{\prime } \right)}^{2}}+{{\left( {{y}_{2}}^{\prime }-{{y}_{1}}^{\prime } \right)}^{2}}}$
$=\sqrt{{{\left( {{x}_{2}}^{\prime }-{{x}_{1}}^{\prime } \right)}^{2}}{{\cos }^{2}}\,\alpha +{{\left( {{y}_{2}}^{\prime }-{{y}_{1}}^{\prime } \right)}^{2}}{{\sin }^{2}}\,\alpha +{{\left( {{x}_{2}}^{\prime }-{{x}_{1}}^{\prime } \right)}^{2}}{{\sin }^{2}}\,\alpha +{{\left( {{y}_{2}}^{\prime }-{{y}_{1}}^{\prime } \right)}^{2}}{{\cos }^{2}}\,\alpha }$
$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\Rightarrow d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .
Câu 15
Cho véc tơ $\overrightarrow{v}=\left( a;b \right)$ sao cho khi phép tịnh tiến đồ thị $y=f\left( x \right)=\dfrac{{{x}^{2}}-x+1}{x-1}$ theo véc tơ $\overrightarrow{v}$ ta nhận đồ thị hàm số \[y=g\left( x \right)=\dfrac{{{x}^{2}}}{x+1}\]. Khi đó tích $a.b$ bằng:
[A]. $1$ .
[B]. $5$ .
[C]. $6$ .
[D]. $4$ .
Đáp án C.
Ta có $g\left( x \right)=f\left( x-a \right)+b$
$\begin{align}
& \Leftrightarrow \dfrac{{{x}^{2}}}{x+1}=\dfrac{{{\left( x-a \right)}^{2}}-\left( x-a \right)+1}{x-a-1}+b \\
& \Leftrightarrow \dfrac{{{x}^{2}}}{x+1}=\dfrac{{{x}^{2}}+\left( -2a+b-1 \right)x+{{a}^{2}}-ab+a-b+1}{x-a-1} \\
\end{align}$
$\Rightarrow \left\{ \begin{align}
& a=-2 \\
& b=-3 \\
\end{align} \right.\Rightarrow a.b=6$ .
Câu 16
Trong mặt phẳng tọa độ\[Oxy\], cho $\overrightarrow{v}=\left( -2;1 \right)$ và đường thẳng $d:2x-3y+3=0$, ${{d}_{1}}:2x-3y-5=0$. Tìm tọa độ $\overrightarrow{w}=\left( a;b \right)$ có phương vuông góc với đường thẳng $d$ để ${{d}_{1}}$ là ảnh của $d$ qua phép tịnh tiến ${{T}_{\overrightarrow{w}}}$. Khi đó $a+b$ bằng:
[A]. $\dfrac{6}{13}$ .
[B]. $\dfrac{16}{13}$.
[C]. $\dfrac{-8}{13}$ .
[D]. $\dfrac{5}{13}$.
Đáp án C.
Đường thẳng $d$ có vectơ pháp tuyến là $\overrightarrow{n}=\left( 2;-3 \right)$ $\Rightarrow \overrightarrow{w}=\left( 2m;-3m \right)$
${{T}_{\overrightarrow{w}}}\left( M \right)={M}’\left( 2m;1-3m \right)$ , với $M\in d$
${{T}_{\overrightarrow{w}}}\left( d \right)={d}’\Rightarrow {d}’$ có dạng $2x-3y+\beta =0$
Vì ${d}’$ qua $M$ $\Rightarrow 4m-3+9m+\beta =0\Leftrightarrow \beta =3-13m$.
$\Rightarrow {d}’:2x-3y+3-13m=0$
Để ${{d}_{1}}\equiv {d}’\Rightarrow 3-13m=-5\Leftrightarrow m=\dfrac{8}{13}$ $\Rightarrow \vec{w}=\left( \dfrac{16}{13};-\dfrac{24}{13} \right)\Rightarrow a+b=-\dfrac{8}{13}$ .
Câu 17
Trong mặt phẳng tọa độ\[Oxy\], cho phép biến hình $F$ xác định như sau: Với mỗi điểm $M\left( x;y \right)$ ta có điểm $M’=F\left( M \right)$ sao cho $M’\left( x’;y’ \right)$ thỏa mãn: $x’=x+2;$ $y’=y-3$. Mệnh đề nào sau đây đúng:
[A]. $F$ là phép tịnh tiến theo $\overrightarrow{v}=\left( 2;3 \right)$ .
[B]. $F$ là phép tịnh tiến theo $\overrightarrow{v}=\left( -2;3 \right)$.
[C]. $F$ là phép tịnh tiến theo $\overrightarrow{v}=\left( 2;-3 \right)$.
[D]. $F$ là phép tịnh tiến theo $\overrightarrow{v}=\left( -2;-3 \right)$.
Đáp án C.
Thật vậy theo biểu thức tọa độ của ${{T}_{\overrightarrow{v}}}\left( M \right)={M}’$ $\left\{ \begin{align}
& {x}’=x+a \\
& {y}’=y+b \\
\end{align} \right.$$\Rightarrow \left\{ \begin{align}
& a=2 \\
& b=-3 \\
\end{align} \right.\Rightarrow \overrightarrow{v}=\left( 2;-3 \right)$.
Câu 18
Trong mặt phẳng tọa độ\[Oxy\], cho hai điểm $A\left( 1;6 \right);B\left( -1;-4 \right)$. Gọi $C,D$ lần lượt là ảnh của $A,B$ qua phép tịnh tiến theo $\overrightarrow{v}=\left( 1;5 \right)$. Kết luận nào sau đây là đúng:
[A]. $ABCD$ là hình vuông.
[B]. $ABCD$ là hình bình hành.
[C]. $ABDC$ là hình bình hành.
[D]. $A,B,C,D$ thẳng hàng.
Đáp án D.
$\begin{align}
& {{T}_{\overrightarrow{v}}}\left( A \right)=C\Rightarrow C\left( 2;11 \right) \\
& {{T}_{\overrightarrow{v}}}\left( B \right)=D\Rightarrow D\left( 0;1 \right) \\
\end{align}$
$\overrightarrow{AB}=\left( -2;-10 \right),\,\,\overrightarrow{CD}=\left( -2;-10 \right),\,\,\overrightarrow{BC}=\left( 3;15 \right)$
$\overrightarrow{AD}=\left( -1;-5 \right)\Rightarrow \overrightarrow{BC}=-3\overrightarrow{AD},\,\,\overrightarrow{AB}=\overrightarrow{CD}$ $\Rightarrow A,\,B,\,C,\,D$ thẳng hàng.
Câu 19
Trong mặt phẳng tọa độ\[Oxy\], cho đường thẳng có phương trình $d:y=2$, và hai điểm $A\left( 1;3 \right);$ $B\left( 3;-4 \right)$. Lấy $M$ trên $d$, $N$ trên trục hoành sao cho $MN$ vuông góc với $d$ và $AM+MN+NB$ nhỏ nhất. Tìm tọa độ $M$, $N$?
[A]. $M\left( \dfrac{6}{5};2 \right),N\left( \dfrac{6}{5};0 \right)$ .
[B]. $M\left( \dfrac{7}{5};2 \right),N\left( \dfrac{7}{5};0 \right)$.
[C]. $M\left( \dfrac{8}{5};2 \right),N\left( \dfrac{8}{5};0 \right)$.
[D]. $M\left( \dfrac{9}{5};2 \right),N\left( \dfrac{9}{5};0 \right)$.
Đáp án B.
Cách 1 : Thử các tọa độ $M,\,N$ ta được kết quả $AM+MN+NB$ nhỏ nhất với $M\in d,\,N\in Ox$ và $MN\bot d$.
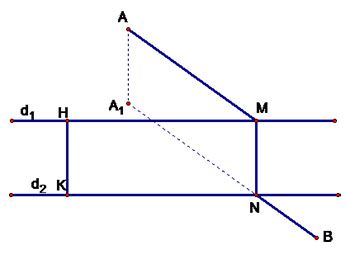
Cách 2 :
Gọi $H\in {{d}_{1}},\,\,K\in {{d}_{2}}$ sao cho $HK\bot {{d}_{1}}$ .
Gọi $T$ là phép tịnh tiến theo vectơ $\overrightarrow{HK}$
Gọi ${{A}_{1}}={{T}_{\overrightarrow{HK}}}\left( A \right),\,{{A}_{1}}B\cap {{d}_{2}}=N,\,\,M\in {{d}_{1}}$ với $MN\bot {{d}_{1}}$
$AM+MN+NB$ nhỏ nhất $\Leftrightarrow AM+NB$ nhỏ nhất ($MN$ không đổi)
$AM+NB={{A}_{1}}N+NB\ge {{A}_{1}}B$
Dấu $”=”$ xảy ra khi $N={{A}_{1}}B\cap {{d}_{2}}$
Lấy ${{A}_{1}}\left( 1;1 \right)$, điểm $N$ cần tìm là giao điểm của ${{A}_{1}}B$ và trục hoành.
Gọi $N\left( {{x}_{0}};0 \right)\Rightarrow \overrightarrow{{{A}_{1}}N}=\left( {{x}_{0}}-1;-1 \right),\,\overrightarrow{{{A}_{1}}B}=\left( 2;-5 \right)$
Vì $\overrightarrow{{{A}_{1}}N}$ và $\overrightarrow{{{A}_{1}}B}$ cùng phương nên $\dfrac{{{x}_{0}}-1}{2}=\dfrac{-1}{-5}\Rightarrow {{x}_{0}}=\dfrac{7}{5}\Rightarrow N\left( \dfrac{7}{5};0 \right)$và $M\left( \dfrac{7}{5};2 \right)$.