Phép tịnh tiến: dạng bài tập cơ bản, trắc nghiệm toán 11
Câu 1
Có bao nhiêu phép tịnh tiến biến đường thẳng thành chính nó?
[A]. $0$.
[B]. $1$.
[C]. $2$.
[D]. Vô số.
Đáp án D.
Khi véc tơ $\overrightarrow{v}$ của phép tịnh tiến ${{T}_{\overrightarrow{v}}}$ có giá song song hoặc trùng với đường thẳng đã cho thì sẽ có vô số phép tịnh tiến biến đường thẳng thành chính nó.
Câu 2
Có bao nhiêu phép tịnh tiến biến đường tròn thành chính nó?
[A]. $0$.
[B]. $1$.
[C]. $2$.
[D]. Vô số.
Đáp án B.
Khi $\overrightarrow{v}=\overrightarrow{0}$: Đường tròn $\left( C \right)$ có tâm $I$ thì ${{T}_{\overrightarrow{v}}}$ biến đường tròn $\left( C \right)$ thành chính nó.
Câu 3
Có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó?
[A]. $0$.
[B]. $1$.
[C]. $2$.
[D]. Vô số.
Đáp án B.
Khi $\overrightarrow{v}=\overrightarrow{0}$ có một phép tịnh tiến biến hình vuông thành chính nó.
Câu 4
Phép tịnh tiến không bảo toàn yếu tố nào sau đây?
[A]. Khoảng cách giữa hai điểm.
[B]. Thứ tự ba điểm thẳng hàng.
[C]. Tọa độ của điểm.
[D]. Diện tích.
Đáp án C.
Khi tọa độ của véc tơ tịnh tiến $\overrightarrow{v}\ne \overrightarrow{0}$.
Câu 5
Với hai điểm $A,\text{ }B$ phân biệt và ${{T}_{\overrightarrow{v}}}\left( A \right)={A}’,\text{ }{{T}_{\overrightarrow{v}}}\left( B \right)={B}’$ với $\overrightarrow{v}\ne \overrightarrow{0}$. Mệnh đề nào sau đây đúng?
[A]. $\overrightarrow{{A}'{B}’}=\overrightarrow{v}$.
[B]. $\overrightarrow{{A}'{B}’}=\overrightarrow{AB}$.
[C]. $\overrightarrow{AB}=\overrightarrow{v}$.
[D]. $\overrightarrow{{A}'{B}’}+\overrightarrow{AB}=\overrightarrow{0}$.
Đáp án B.
Ta chỉ ra được $ABB’A’$ là hình bình hành $\Rightarrow \overrightarrow{A’B’}=\overrightarrow{AB}$
Câu 6
Cho hai đường thẳng ${{d}_{1}}$ và ${{d}_{2}}$ song song với nhau. Có bao nhiêu phép tịnh tiến theo vectơ $\overrightarrow{v}\ne \overrightarrow{0}$ biến ${{d}_{1}}$ thành ${{d}_{2}}$?
[A]. $0$.
[B]. $1$.
[C]. $2$.
[D]. Vô số.
Đáp án D.
Chẳng hạn lấy bất kỳ $A\in {{d}_{1}}$, $B\in {{d}_{2}}$ $\Rightarrow {{T}_{\overrightarrow{AB}}}\left( {{d}_{1}} \right)$ thành ${{d}_{2}}$ nên có vô số phép tịnh tiến thỏa mãn.
Câu 7
Cho hình bình hành $ABCD$. Phép tịnh tiến ${{T}_{\overrightarrow{AB}+\overrightarrow{AD}}}$ biến điểm $A$ thành điểm nào?
[A]. ${A}’$ đối xứng với $A$ qua $C$.
[B]. ${A}’$ đối xứng với $D$ qua $C$.
[C]. $O$ là giao điểm của $AC$ qua $BD$.
[D]. $C$.
Đáp án D.
Ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\Rightarrow {{T}_{\overrightarrow{AC}}}\left( A \right)=C$.
Câu 8
Cho tam giác $ABC$ có trọng tâm $G$, ${{T}_{\overrightarrow{AG}}}\left( G \right)=M$. Mệnh đề nào là đúng?
[A]. $M$là trung điểm $BC$.
[B]. $M$ trùng với $A$.
[C]. $M$ là đỉnh thứ tư của hình bình hành $BGCM$.
[D]. $M$ là đỉnh thứ tư của hình bình hành $BCGM$.
Đáp án C.
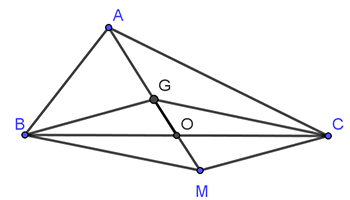
Ta có ${{T}_{\overrightarrow{AG}}}\left( G \right)=M\Leftrightarrow \overrightarrow{AG}=\overrightarrow{GM}\Rightarrow BGCM$ là hình bình hành.
Câu 9
Cho lục giác đều $ABCDEF$ tâm $O$. Tìm ảnh của $\Delta AOF$ qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$.
[A]. $\Delta AOB$.
[B]. $\Delta BOC$.
[C]. $\Delta CDO$.
[D]. $\Delta DEO$.
Đáp án B.
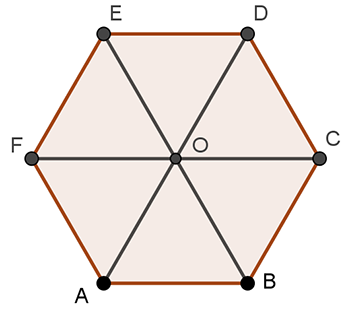
Ta có $\left\{ \begin{align}
& {{T}_{\overrightarrow{AB}}}\left( A \right)=B \\
& {{T}_{\overrightarrow{AB}}}\left( O \right)=C \\
& {{T}_{\overrightarrow{AB}}}\left( F \right)=O \\
\end{align} \right.$$\Rightarrow {{T}_{\overrightarrow{AB}}}\left( \Delta AOF \right)=\Delta BCO$ .
Câu 10
Cho hình bình hành $ABCD$ tâm $I$. Kết luận nào sau đây sai?
[A]. ${{T}_{\overrightarrow{DC}}}\left( A \right)=B$.
[B]. ${{T}_{\overrightarrow{CD}}}\left( B \right)=A$.
[C]. ${{T}_{\overrightarrow{DI}}}\left( I \right)=B$.
[D]. ${{T}_{\overrightarrow{IA}}}\left( I \right)=C$.
Đáp án D.
Ta có ${{T}_{\overrightarrow{IA}}}\left( I \right)=A$ nên đáp án D sai.
Câu 11
Cho hình vuông $ABCD$ tâm $I$. Gọi $M,\text{ }N$lần lượt là trung điểm của $AD,\text{ }DC$. Phép tịnh tiến theo vectơ nào sau đây biến $\Delta AMI$ thành $\Delta MDN$?
[A]. $\overrightarrow{AM}$.
[B]. $\overrightarrow{NI}$.
[C]. $\overrightarrow{AC}$.
[D]. $\overrightarrow{MN}$.
Đáp án A.
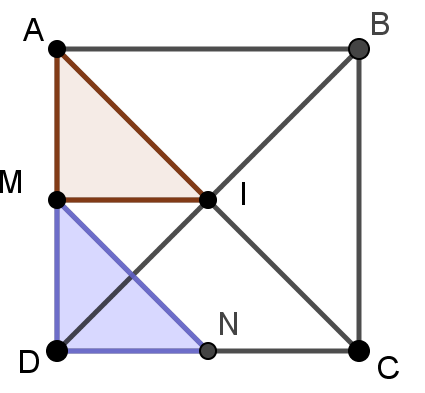
Từ hình vẽ ta có ${{T}_{\overrightarrow{AM}}}\left( \Delta AMI \right)=\Delta MDN$.
Câu 12
Cho hình bình hành $ABCD$. Có bao nhiêu phép tịnh tiến biến đường thẳng $AB$ thành đường thẳng $CD$ và biến đường thẳng $AD$ thành đường thẳng $BC$?
[A]. $0$.
[B]. $1$.
[C]. $2$.
[D]. Vô số.
Đáp án B.

Từ hình vẽ ta có
${{T}_{\overrightarrow{BC}}}\left( AB \right)=CD$ với $AB,\,CD$ là các đoạn thẳng.
${{T}_{\overrightarrow{BC}}}\left( AB \right)=CD$, với $AD,\,BC$ là đoạn thẳng nên có một phép tịnh tiến thỏa mãn.
Câu 13
Cho đường tròn $\left( O \right)$ và hai điểm $A,\text{ }B$. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Tìm quỹ tích điểm ${M}’$sao cho $\overrightarrow{M{M}’}+\overrightarrow{MA}=\overrightarrow{MB}$.
[A]. $\left( {{O}’} \right)={{T}_{\overrightarrow{AB}}}\left( \left( O \right) \right)$.
[B]. $\left( {{O}’} \right)={{T}_{\overrightarrow{AM}}}\left( \left( O \right) \right)$.
[C]. $\left( {{O}’} \right)={{T}_{\overrightarrow{BA}}}\left( \left( O \right) \right)$.
[D]. $\left( {{O}’} \right)={{T}_{\overrightarrow{BM}}}\left( \left( O \right) \right)$.
Đáp án A.
Ta có : $\overrightarrow{M{M}’}+\overrightarrow{MA}=\overrightarrow{MB}\Leftrightarrow \overrightarrow{M{M}’}=\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AB}\Leftrightarrow {{T}_{\overrightarrow{AB}}}\left( M \right)={M}’$.
Vậy tập hợp điểm ${M}’$ là ảnh của đường tròn $\left( O \right)$ qua ${{T}_{\overrightarrow{AB}}}$ .
Câu 14
Cho tứ giác lồi $ABCD$ có $AB=BC=CD=a$, $\widehat{BAD}=75{}^\circ $ và $\widehat{ADC}=45{}^\circ $.Tính độ dài $AD$.
[A]. $a\sqrt{2+\sqrt{5}}$.
[B]. $a\sqrt{3}$.
[C]. $a\sqrt{2+\sqrt{3}}$.
[D]. $a\sqrt{5}$.
Đáp án C.
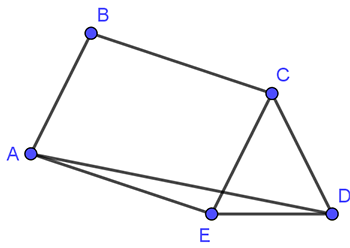
Xét ${{T}_{\overrightarrow{BC}}}\left( A \right)={A}’.$
Khi đó $C{A}’=BA=CD\Rightarrow \Delta C{A}’D$ cân tại $C$.
$\Rightarrow \widehat{{A}’CD}={{60}^{0}}\Rightarrow \Delta C{A}’D$ đều.
$\Rightarrow \widehat{{A}’DA}={{15}^{0}}$ và \[A{A}’=BC=CD={A}’D=a\]
\[\Rightarrow \widehat{A{A}’D}={{150}^{0}}\]
Do đó $A{{D}^{2}}=2{A}'{{A}^{2}}-2{A}'{{A}^{2}}\cos A{A}’D=2{{a}^{2}}+\sqrt{3}{{a}^{2}}$ (áp dụng định lí cosin).
$\Rightarrow AD=a\sqrt{2+\sqrt{3}}$.
Câu 15
Cho tứ giác $ABCD$ có $AB=6\sqrt{3},\text{ }CD=12$, $\widehat{A}=60{}^\circ ,\text{ }\widehat{B}=150{}^\circ ,\text{ }\widehat{D}=90{}^\circ $. Tính độ dài $BC$.
[A]. $4$.
[B]. $5$.
[C]. $6$.
[D]. $2$.
Đáp án C.
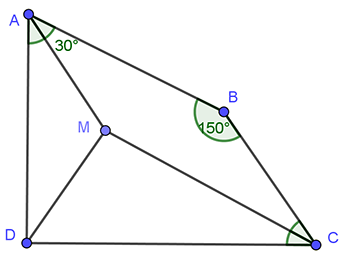
Xét ${{T}_{\overrightarrow{BC}}}\left( A \right)=M\Rightarrow ABCM$ là hình bình hành.
$\Rightarrow \widehat{BCM}={{30}^{0}}\Rightarrow \widehat{BCD}={{60}^{0}}$ và $\widehat{MCD}={{30}^{0}}$
Ta có $M{{D}^{2}}=M{{C}^{2}}+D{{C}^{2}}-2MC.DC.\cos {{30}^{0}}=36\Rightarrow MD=6$
$MD=\dfrac{1}{2}CD$ và $MC=MD\sqrt{3}$ $\Rightarrow \Delta MDC$ là nửa tam giác đều.
$\Rightarrow \widehat{DMC}={{90}^{0}}\,\Rightarrow \widehat{MDA}={{30}^{0}}$
Vậy $\widehat{MDA}=\widehat{MAD}=\widehat{MAB}={{30}^{0}}\Rightarrow \Delta AMD$ cân tại $M$$\Rightarrow BC=MA=MD=6$.
Câu 16
Trên đoạn $AD$ cố định dựng hình bình hành $ABCD$ sao cho $\dfrac{AC}{AD}=\dfrac{BD}{AB}$. Tìm quỹ tích đỉnh $C$.
[A]. Đường tròn tâm $A$, bán kính là $AB\sqrt{3}$.
[B]. Đường tròn tâm $A$, bán kính là $AC$.
[C]. Đường tròn tâm $A$, bán kính là $AD$.
[D]. Đường tròn tâm $A$, bán kính là $AD\sqrt{2}$.
Đáp án D.
Chọn hệ trục về chiều dương như hình vẽ.
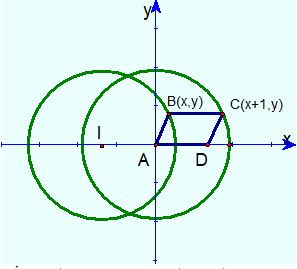
Cố định $D\left( 1;0 \right)$. Với $B\left( x;y \right)\Rightarrow C\left( x+1;y \right)$
Từ giả thiết $AC.AB=AD.BD$
$\begin{align}
& \Leftrightarrow \sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}.\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}} \\
& \Leftrightarrow \left( {{x}^{2}}+{{y}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}}+2x \right)=1-2x \\
& \Leftrightarrow \left( {{x}^{2}}+{{y}^{2}}+1 \right)\left( {{x}^{2}}+{{y}^{2}}+2x \right)-{{x}^{2}}-{{y}^{2}}-2x=1-2x \\
\end{align}$
$\Leftrightarrow \left( {{x}^{2}}+{{y}^{2}}+1 \right)\left( {{x}^{2}}+{{y}^{2}}+2x-1 \right)=0$ (do \[{{x}^{2}}+{{y}^{2}}+1>0\]).
$\Leftrightarrow {{x}^{2}}+{{y}^{2}}+2x-1=0\Leftrightarrow {{\left( x+1 \right)}^{2}}+{{y}^{2}}=2\,\,\,(1)$.
Suy ra quỹ tích $B$ là đường tròn tâm $I$ , bán kính $\sqrt{2}$ ($I$ là điểm đối xứng của $D$ qua $A$)
Ta có ${{T}_{\overrightarrow{BC}}}\left( B \right)=C$
Vậy quỹ tích của $C$ là đường tròn tâm $A$ , bán kính $AD\sqrt{2}$ .
Câu 17
Cho hai đường tròn có bán kính $R$ cắt nhau tại $M,\text{ }N$. Đường trung trực của $MN$ cắt các đường tròn tại $A$ và $B$ sao cho $A,\text{ }B$ nằm cùng một phía với $MN$. Tính $P=M{{N}^{2}}+A{{B}^{2}}$.
[A]. $P=2{{R}^{2}}$.
[B]. $P=3{{R}^{2}}$.
[C]. $P=4{{R}^{2}}$.
[D]. $P=6{{R}^{2}}$.
Đáp án C.
Giả sử trung trực $MN$ cắt $\left( {{O}_{1}} \right)$ tại $A$ , cắt $\left( {{O}_{2}} \right)$ tại $B$ (${{O}_{1}}$ ở giữa $A,\,B$)
(Bạn đọc tự vẽ hình)
Thực hiện phép trịnh tiến theo vectơ $\overrightarrow{{{O}_{2}}{{O}_{1}}}$ đường tròn $\left( {{O}_{2}} \right)$ biến thành đường tròn $\left( {{O}_{1}} \right)$ . vì vậy $B$ biến thành $A$ , $M$ biến trhành ${{M}_{1}}$ , $N$ biến thành ${{N}_{1}}$ .
$MN{{N}_{1}}{{M}_{1}}$ là hình bình hành nội tiếp nên là hình chữ nhật. Vậy $M{{N}^{2}}+{{M}_{1}}{{M}^{2}}=M{{N}^{2}}+A{{B}^{2}}=4{{R}^{2}}$.
Câu 18
Cho hai đường tròn có bán kính $R$ tiếp xúc ngoài với nhau tại $K$. Trên đường tròn này lấy điểm $A$, trên đường tròn kia lấy điểm $B$ sao cho $\widehat{AKB}=90{}^\circ $. Độ dài $AB$ bằng bao nhiêu?
[A]. $R$.
[B]. $R\sqrt{2}$.
[C]. $R\sqrt{3}$.
[D]. $2R$.
Đáp án D.
(Bạn đọc tự vẽ hình).
Sử dụng phép tịnh tiến theo vectơ $\overrightarrow{{{O}_{1}}{{O}_{2}}}$ thì $K$ biến thành $C$, $KA$ thành $CB$. Vì vậy $AB=2R$ .
Câu 19
Từ đỉnh $B$ của hình bình hành $ABCD$ kẻ các đường cao $BK$ và $BH$của nó biết $KH=3,\text{ }BD=5$. Khoảng cách từ $B$ đến trực tâm ${{H}_{1}}$ của tam giác $BKH$ có giá trị bằng bao nhiêu?
[A]. $4$ .
[B]. $5$ .
[C]. $6$.
[D]. $4,5$.
Đáp án A.
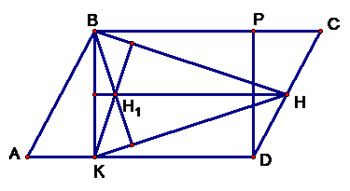
Thực hiện phép tịnh tiến theo vectơ $\overrightarrow{KD}$ ta có :
$K$ biến thành $D$ , ${{H}_{1}}$ biến thành $H$ , $B$ biến thành $P$
Ta có $\Delta PHK$ vuông tại $H$ và $KH=3,KP=BD=5$ nên $PH=\sqrt{25-9}=4\Rightarrow B{{H}_{1}}=PH=4$.