Tính đơn điệu của hàm số lượng giác, trắc nghiệm toán 11
Phương pháp chung:
Ở phần lý thuyết, với các hàm số lượng giác cơ bản, ta đã biết rằng:
- Hàm số $y=\sin x:$
* Đồng biến trên các khoảng $\left( -\dfrac{\pi }{2}+k2\pi ;\,\,\dfrac{\pi }{2}+k2\pi \right),\,k\in \mathbb{Z}.$
* Nghịch biến trên các khoảng $\left( \dfrac{\pi }{2}+k2\pi ;\,\,\dfrac{3\pi }{2}+k2\pi \right),\,k\in \mathbb{Z}.$
- Hàm số $y=\cos x:$
* Đồng biến trên các khoảng $\left( -\pi +k2\pi ;\,\,k2\pi \right),\,k\in \mathbb{Z}.$
* Nghịch biến trên các khoảng $\left( k2\pi ;\,\,\pi +k2\pi \right),\,k\in \mathbb{Z}.$
- Hàm số $y=\tan x$ đồng biến trên các khoảng $\left( -\dfrac{\pi }{2}+k\pi ;\,\,\dfrac{\pi }{2}+k\pi \right),\,k\in \mathbb{Z}.$
- Hàm số $y=\cot x$ nghịch biến trên các khoảng $\left( k\pi ;\,\,\pi +k\pi \right),\,k\in \mathbb{Z}.$
Với các hàm số lượng giác phức tạp, để xét tính đơn điệu của nó ta sử dụng định nghĩa.
Câu 1.
Trong khoảng \[\left( 0;\dfrac{\pi }{2} \right)\], hàm số \[y=\sin x-\cos x\]là hàm số:
[A]. Đồng biến.
[B]. Nghịch biến.
[C]. Không đổi.
[D]. Vừa đồng biến vừa nghịch biến.
Đáp án A.
Cách 1 : Ta thấy trên khoảng $\left( 0;\dfrac{\pi }{2} \right)$ hàm $f(x)=\sin x$ đồng biến và hàm $g(x)=-\cos x$đồng biến , suy ra trên $\left( 0;\dfrac{\pi }{2} \right)$ hàm số $y=\sin x-\cos x$ đồng biến.
Cách 2 : Sử dụng máy tính . Dùng TABLE ta xác định được hàm số $y=\sin x-\cos x$tăng trên $\left( 0;\dfrac{\pi }{2} \right)$
Câu 2.
Hàm số \[y=\sin 2x\]nghịch biến trên các khoảng nào sau đây \[\left( k\in Z \right)\]?
[A]. \[\left( k2\pi ;\pi +k2\pi \right)\].
[B]. \[\left( \dfrac{\pi }{4}+k\pi ;\dfrac{3\pi }{4}+k\pi \right)\].
[C]. \[\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)\].
[D]. \[\left( -\dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{4}+k\pi \right)\].
Đáp án C .
Ta thấy hàm số $y=\sin 2x$ nghịch biến trên $\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right),k\in \mathbb{Z}$, suy ra hàm số $y=\sin 2x$nghịch biến khi $\dfrac{\pi }{2}+k2\pi <2x<\dfrac{3\pi }{2}+k2\pi \Leftrightarrow \dfrac{\pi }{4}+k\pi <x<\dfrac{3\pi }{4}+k\pi ,k\in \mathbb{Z}$
Vậy hàm số $y=\sin 2x$ nghịch biến trên mỗi khoảng $\left( \dfrac{\pi }{4}+k\pi ;\dfrac{3\pi }{4}+k\pi \right),k\in \mathbb{Z}$
Câu 3.
Hàm số \[y=\cos 2x\] nghịch biến trên khoảng \[\left( k\in Z \right)\]?
[A]. \[\left( k\pi ;\dfrac{\pi }{2}+k\pi \right)\].
[B]. \[\left( \dfrac{\pi }{2}+k\pi ;\pi +k\pi \right)\].
[C]. \[\left( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right)\].
[D]. \[\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)\].
Đáp án A.
Hàm số \[y=\cos 2x\] nghịch biến khi $k2\pi <2x<\pi +k2\pi \Leftrightarrow k\pi <x<\dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}$
Câu 4.
Xét các mệnh đề sau:
(I): \[\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right)\]:Hàm số \[y=\dfrac{1}{\sin x}\] giảm.
(II): \[\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right)\]:Hàm số \[y=\dfrac{1}{\cos x}\] giảm.
Hãy chọn mệnh đề đúng trong các mệnh đề trên:
[A]. Chỉ (I) đúng .
[B]. Chỉ (II) đúng .
[C]. Cả hai đúng.
[D]. Cả hai sai.
Đáp án B.
$\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right)$ : Hàm $y=\sin x$ giảm và $\sin x<0$, suy ra $y=\dfrac{1}{\sin x}$ tăng:Câu (I) sai
$\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right)$ : Hàm $y=\cos x$ tăng và $\cos x<0$, suy ra hàm$y=\dfrac{1}{\cos x}$ giảm. Câu (II) đúng.
Câu 5.
Cho hàm số \[y=4\sin \left( x+\dfrac{\pi }{6} \right)\cos \left( x-\dfrac{\pi }{6} \right)-\sin 2x\]. Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?
[A]. Hàm số đã cho đồng biến trên các khoảng \[\left( 0;\dfrac{\pi }{4} \right)\] và \[\left( \dfrac{3\pi }{4};\pi \right)\].
[B]. Hàm số đã cho đồng biến trên \[\left( 0;\pi \right)\].
[C]. Hàm số đã cho nghịch biến trên khoảng \[\left( 0;\dfrac{3\pi }{4} \right)\] .
[D]. Hàm số đã cho đồng biến trên khoảng \[\left( 0;\dfrac{\pi }{4} \right)\] và nghịch biến trên khoảng\[\left( \dfrac{\pi }{4};\pi \right)\].
Đáp án A.
Ta có $y=4\sin (x+\dfrac{\pi }{6})\cos (x-\dfrac{\pi }{6})-\sin 2x=2(\sin 2x+\sin \dfrac{\pi }{3})-\sin 2x=\sin 2x+\sqrt{3}$
. Xét sự biến thiên của hám số $y=\sin 2x+\sqrt{3}$ , ta sử dụng TABLE để xét các mệnh đề .
Ta thấy với [A]. Trên $\left( 0;\dfrac{\pi }{4} \right)$ thì giá trị của hàm số luôn tăng.
Tương tự trên $\left( \dfrac{3\pi }{4};\pi \right)$ thì giá trị của hàm số cũng luôn tăng.
Câu 6.
Với \[k\in Z\], kết luận nào sau đây về hàm số \[y=\tan 2x\] là sai?
[A]. Hàm số \[y=\tan 2x\]tuần hoàn với chu kỳ \[T=\dfrac{\pi }{2}\].
[B]. Hàm số \[y=\tan 2x\]luôn dống biến trên mỗi khoảng \[\left( -\dfrac{\pi }{2}+\dfrac{k\pi }{2};\dfrac{\pi }{2}+\dfrac{k\pi }{2} \right)\].
[C]. Hàm số \[y=\tan 2x\]nhận đường thẳng \[x=\dfrac{\pi }{4}+\dfrac{k\pi }{2}\]là một đường tiệm cận.
[D]. Hàm số \[y=\tan 2x\] là hàm số lẻ.
Đáp án B.
Ta thấy hàm số $y=\tan x$ luôn đồng biến trên mỗi khoảng \[\left( \dfrac{-\pi }{2}+k\pi ;\dfrac{\pi }{2}+k\pi \right)\], suy ra hàm số $y=\tan 2x$ luôn đồng biến tren mỗi khoảng \[\dfrac{-\pi }{2}+k\pi <2x<\dfrac{\pi }{2}+k\pi \Leftrightarrow \dfrac{-\pi }{4}+\dfrac{k\pi }{2}<x<\dfrac{\pi }{4}+\dfrac{k\pi }{2}\]. Vậy B là sai.
Câu 7.
Để hàm số \[y=\sin x+\cos x\] tăng, ta chọn x thuộc khoảng nào?
[A]. \[\left( -\dfrac{3\pi }{4}+k2\pi ;\dfrac{\pi }{4}+k2\pi \right)\] .
[B]. \[\left( -\dfrac{3\pi }{4}+k\pi ;\dfrac{\pi }{4}+k\pi \right)\] .
[C]. \[\left( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right)\] .
[D]. \[\left( \pi +k2\pi ;2\pi +k2\pi \right)\] .
Đáp án A.
Ta có $y=\sin x+\cos x=\sqrt{2}\cos \left( x+\dfrac{\pi }{4} \right)$. Để hàm số $y=\sin x+\cos x$ tăng thì
$\dfrac{-\pi }{2}+k2\pi <x+\dfrac{\pi }{4}<\dfrac{\pi }{2}+k2\pi \Leftrightarrow \dfrac{-3\pi }{4}+k2\pi <x<\dfrac{\pi }{4}+k2\pi $
Câu 8.
Xét hai mệnh đề sau:
(I): \[\forall x\in \left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)\]:Hàm số \[y={{\tan }^{2}}x\] tăng.
(II): \[\forall x\in \left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)\]:Hàm số \[y={{\sin }^{2}}x\] tăng.
Hãy chọn mệnh đề đúng trong các mệnh đề trên:
[A]. Chỉ (I) đúng .
[B]. Chỉ (II) đúng .
[C]. Cả hai đúng.
[D]. Cả hai sai.
Đáp án C.
Bài toán có hai hàm số mà cùng xét trên một khoảng nên ta sẽ sử dụng chức năng TABLE cho hai hàm Ấn MODE7 : Nhập f(x) là hàm ${{\tan }^{2}}x$ nhập g(x) là hàm ${{\sin }^{2}}x$ thì ta có kết quả .
Ta thấy cả hai hàm số đều không là hàm tăng trên cả khoảng \[\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)\]. Vì khi x chạy từ $\dfrac{-\pi }{2}$ đến 0 thì giá trị của hai hàm số đều giảm . Khi x chạy từ 0 đến $\dfrac{\pi }{2}$ thì giá trị của hai hàm số đều tăng , vậy cả hai mệnh đề đều sai.
Câu 9.
Hãy chọn câu sai: Trong khoảng \[\left( \dfrac{\pi }{2}+k2\pi ;\pi +k2\pi \right),k\in Z\]thì:
[A]. Hàm số \[y=\sin x\] là hàm số nghịch biến .
[B]. Hàm số \[y=\cos x\] là hàm số nghịch biến.
[C]. Hàm số \[y=\tan x\] là hàm số đồng biến.
[D]. Hàm số \[y=\cot x\] là hàm số đồng biến .
Đáp án D.
D sai, với $\dfrac{2\pi }{3};\dfrac{3\pi }{4}\in \left( \dfrac{\pi }{2};\pi \right)$, ta có: $\dfrac{2\pi }{3}<\dfrac{3\pi }{4}=>\cot \dfrac{2\pi }{3}=\dfrac{-\sqrt{3}}{3}>-1=\cot \dfrac{3\pi }{4}$
Câu 10.
Bảng biến thiên của hàm số \[y=f(x)=\cos 2x\]trên đoạn \[\left[ -\dfrac{\pi }{2};\dfrac{3\pi }{2} \right]\] là:
[A]. 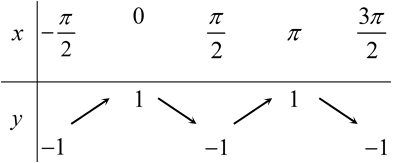
[B]. 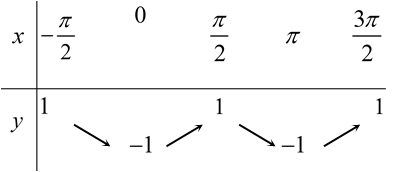
[C]. 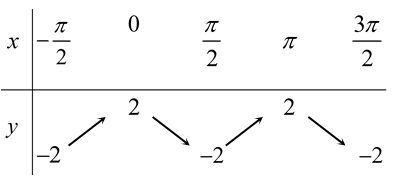
[D]. 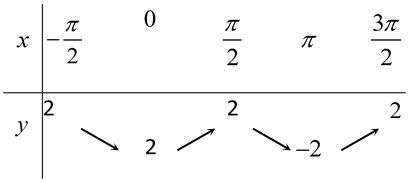
Đáp án A.
Ta có thể loại phương án B ;C ;D luôn do tại $f(0)=\cos 0=1$ và $f(\pi )=\cos 2\pi =1$. Các bảng biến thiên B ;C ;D đều không thỏa mãn.
Câu 11.
Cho hàm số \[y=\cos \dfrac{x}{2}\]. Bảng biến thiên của hàm số trên đoạn\[\left[ -\pi ;\pi \right]\]là:
[A]. 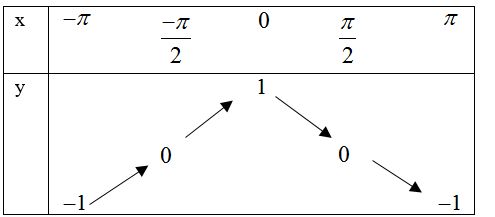
[B]. 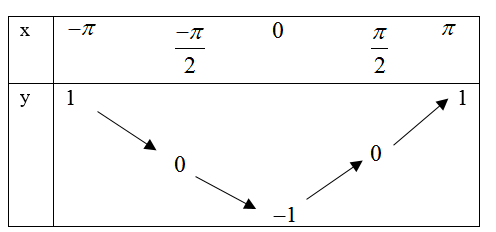
[C]. 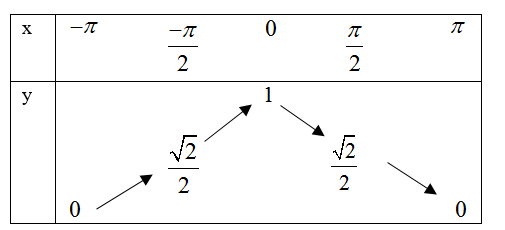
[D]. 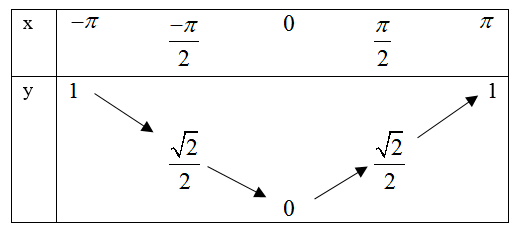
Đáp án C.
Tương tự như câu 10 thì ta có thể loại A và B do $f\left( \dfrac{\pi }{2} \right)=\cos \left( \dfrac{-\pi }{4} \right)=\dfrac{\sqrt{2}}{2}$
tiếp theo xét giá trị hàm số tại hai đâu mút thì ta loại được D.