Tập xác định của hàm số lượng giác, trắc nghiệm toán 11
| Cách 1 Tìm tập $D$ của \[\text{x}\] để $f\left( x \right)$ có nghĩa, tức là tìm \[\text{D}=\left\{ x\in \mathbb{R}\left| f\left( x \right)\in \mathbb{R} \right. \right\}\] . | Cách 2 Tìm tập $E$ của \[\text{x}\] để $f\left( x \right)$ không có nghĩa, khi đó tập xác định của hàm số là \[\text{D}=\mathbb{R}\backslash E\]. |
[A]. Với hàm số \[f\left( x \right)\] cho bởi biểu thức đại số thì ta có:
$f\left( x \right)=\dfrac{{{f}_{1}}\left( x \right)}{{{f}_{2}}\left( x \right)}$, điều kiện:
* ${{f}_{1}}\left( x \right)$ có nghĩa
* ${{f}_{2}}\left( x \right)$ có nghĩa và ${{f}_{2}}\left( x \right)\ne 0$.
- $f\left( x \right)=\sqrt[2m]{{{f}_{1}}\left( x \right)},\left( m\in \mathbb{N} \right)$, điều kiện: ${{f}_{1}}\left( x \right)$ có nghĩa và ${{f}_{1}}\left( x \right)\ge 0$.
- $f\left( x \right)=\dfrac{{{f}_{1}}\left( x \right)}{\sqrt[2m]{{{f}_{2}}\left( x \right)}},\left( m\in \mathbb{N} \right)$, điều kiện: ${{f}_{1}}\left( x \right),{{f}_{2}}\left( x \right)$ có nghĩa và ${{f}_{2}}\left( x \right)>0$.
[B]. Hàm số $y=\sin x;y=\cos x$ xác định trên \[\mathbb{R}\], như vậy
$y=\sin \left[ u\left( x \right) \right];y=\cos \left[ u\left( x \right) \right]$ xác định khi và chỉ khi $u\left( x \right)$ xác định.
* $y=\tan \left[ u\left( x \right) \right]$ có nghĩa khi và chỉ khi $u\left( x \right)$ xác định và $u\left( x \right)\ne \dfrac{\pi }{2}+k\pi ;k\in \mathbb{Z}$.
* $y=\cot \left[ u\left( x \right) \right]$ có nghĩa khi và chỉ khi $u\left( x \right)$ xác định và $u\left( x \right)\ne +k\pi ;k\in \mathbb{Z}$.
BÀI TẬP VẬN DỤNG TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC
Câu 1.
Tập xác định của hàm số $y=\dfrac{1}{2\cos x-1}$ là:
[A]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{\pi }{3}+k2\pi ,\dfrac{5\pi }{3}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
[B]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{\pi }{3}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
[C]. \[\text{D}=\left\{ \dfrac{\pi }{3}+k2\pi ,\dfrac{5\pi }{3}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
[D]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{5\pi }{3}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
Cách 1: Hàm số đã cho xác định khi
$2\cos x-1\ne 0\Leftrightarrow \left\{ \begin{align}
\cos x\ne \cos \dfrac{\pi }{3} \\
\cos x\ne \cos \dfrac{5\pi }{3} \\
\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}
x\ne \dfrac{\pi }{3}+k2\pi \\
x\ne \dfrac{5\pi }{3}+k2\pi \\
\end{align} \right.,k\in \mathbb{Z}$
Cách 2: Sử dụng máy tính cầm tay tính giá trị của hàm số $y=\dfrac{1}{2\cos x-1}$ tại $x=\dfrac{\pi }{3}$ và $x=\dfrac{5\pi }{3}$ ta thấy hàm số đều không xác định, từ đây ta chọn A.
Ghi chú:
Đối với hàm côsin, trong một chu kỳ tuần hoàn của hàm số $\left[ 0;2 \right]$ tồn tại hai góc có số đo là $\dfrac{\pi }{3}$ và $\dfrac{5\pi }{3}$ cùng thỏa mãn $\cos \dfrac{\pi }{3}=\cos \dfrac{5\pi }{3}=\dfrac{1}{2}$ chính vì thế ta kết luận được điều kiện như vậy.
Cách bấm như sau:
Nhập vào màn hình $\dfrac{1}{2\cos \left( \text{X} \right)-1}$:
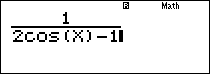
Ấn r gán $X=\dfrac{\pi }{3}$ thì máy báo lỗi, tương tự với trường hợp $X=\dfrac{5\pi }{3}$.

Từ đây suy ra hàm số không xác định tại $\dfrac{\pi }{3}$ và $\dfrac{5\pi }{3}$.
Câu 2.
Tập xác định của hàm số $y=\dfrac{\cot x}{\sin x-1}$ là:
[A]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{\pi }{3}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
[B]. \[\text{D}=\mathbb{R}\backslash \left\{ k\dfrac{\pi }{2}\left| k\in \mathbb{Z} \right. \right\}\].
[C]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi ;\pi \left| k\in \mathbb{Z} \right. \right\}\].
[D]. \[\text{D}=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
Hàm số đã cho xác định khi
+ $\cot x$ xác định $\Leftrightarrow \sin x\ne 0$
+ \[\sin x-1\ne 0\]
$\Leftrightarrow \left\{ \begin{align}
\sin x\ne 0 \\
\sin x\ne 1 \\
\end{align} \right. $
$\Leftrightarrow \left\{ \begin{align}
x\ne k\pi \\
x\ne \dfrac{\pi }{2}+k2\pi \\
\end{align} \right.,k\in \mathbb{Z}$ .
Câu 3.
Tập hợp $\mathbb{R}\backslash \left\{ k\pi \left| k\in \mathbb{Z} \right. \right\}$ không phải là tập xác định của hàm số nào?
[A]. \[y=\dfrac{1-\cos x}{\sin x}\].
[B]. \[y=\dfrac{1-\cos x}{2\sin x}\].
[C]. \[y=\dfrac{1+\cos x}{\sin 2x}\].
[D]. \[y=\dfrac{1+\cos x}{\sin x}\].
$\sin 2x\ne 0\Leftrightarrow
\left[ \begin{align}
\sin 2x\ne \sin 0 \\
\sin 2x\ne \sin \pi
\end{align} \right.$$\Leftrightarrow \left[ \begin{align}
2x\ne k2\pi \\
2x\ne \pi +k2\pi
\end{align} \right.$$\Leftrightarrow x\ne \dfrac{k\pi }{2},\,k\in \mathbb{Z}$
$\sin x\ne 0 \Leftrightarrow\left[ \begin{align}
\sin x\ne \sin 0 \\
\sin x\ne \sin \pi
\end{align} \right.$$\Leftrightarrow \left[ \begin{align}
x\ne k2\pi \\
x\ne \pi +k2\pi
\end{align} \right.$$\Leftrightarrow x\ne k\pi ,\,k\in \mathbb{Z}$
Phân tích: Với các bài toán dạng này nếu ta để ý một chút thì sẽ thấy hàm $\cos x$ xác định với mọi $x\in \mathbb{R}$. Nên ta chỉ xét mẫu số, ở đây có đến ba phương án có mẫu số có chứa $\sin x$ như nhau là $A;\,D$ và $B$. Do đó ta chọn được luôn đáp án $C$
Trong ví dụ trên ta có thể gộp hai họ nghiệm $k2\pi $ và $\pi +k2\pi $ thành $k\pi $ dựa theo lý thuyết sau:
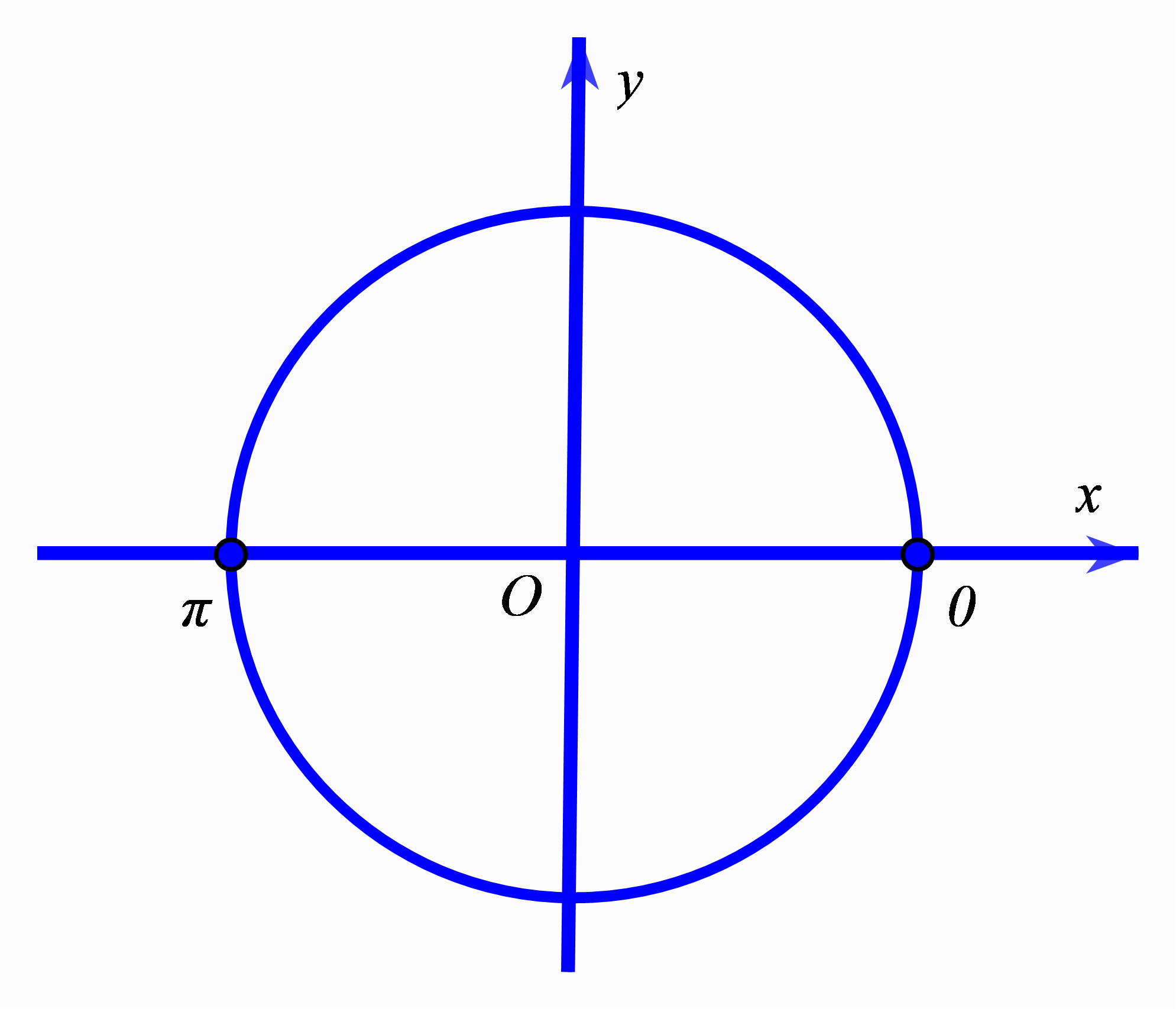
Mỗi cung (hoặc góc) lượng giác được biểu diễn bởi một điểm trên đường tròn lượng giác
$*\,x=\alpha +k2\pi ,\,k\in \mathbb{Z}$ được biểu diễn bởi một điểm trên đường tròn lượng giác.
$*\,x=\alpha +k\pi ,\,k\in \mathbb{Z}$ được biểu diễn bởi hai điểm đối xứng nhau qua $O$ trên đường tròn lượng giác.
$*\,x=\alpha +\dfrac{k2\pi }{3},\,k\in \mathbb{Z}$ được biểu diễn bởi ba điểm cách đều nhau, tạo thành $3$ đỉnh của một tam giác đều nội tiếp đường tròn lượng giác.
$*\,x=\alpha +\dfrac{k2\pi }{n},\,k\in \mathbb{Z},\,n\in {{\mathbb{N}}^{*}}$ được biểu diễn bởi $n$ điểm cách đều nhau, tạo thành $n$ đỉnh của một đa giác đều nội tiếp đường tròn lượng giác.
Giải thích cách gộp nghiệm ở ví dụ 3 ta có
Trên hình 1.11 hai chấm tròn đen là điểm biểu diễn hai nghiệm ta tìm được ở ví dụ 3. Từ đây nếu gộp nghiệm lại thì ta sẽ có $x=0+\dfrac{k2\pi }{2}=k\pi ,\,k\in \mathbb{Z}$.
Câu 4.
Tìm tập xác định của hàm số $y=\sin \dfrac{1}{x}+2x$
[A]. \[D=\left[ -2;\,2 \right]\].
[B]. \[D=\left[ -1;\,1 \right]\backslash \left\{ 0 \right\}\].
[C]. \[D=\mathbb{R}\].
[D]. \[D=\mathbb{R}\backslash \left\{ 0 \right\}\].
Chọn D.
Hàm số đã cho xác định khi $\sin \dfrac{1}{x}$ xác định$\Leftrightarrow x\ne 0$
Câu 5.
Tập xác định của hàm số $y=2016{{\tan }^{2017}}2x$ là
[A]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi \left| k\in \mathbb{Z} \right. \right\}\].
[B]. \[D=\mathbb{R}\backslash \left\{ k\dfrac{\pi }{2}\left| k\in \mathbb{Z} \right. \right\}\].
[C]. \[D=\mathbb{R}\].
[D]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k\dfrac{\pi }{2}\left| k\in \mathbb{Z} \right. \right\}\].
Chọn D.
Ta có $y=2016{{\tan }^{2017}}2x=2016.{{\left( \tan 2x \right)}^{2017}}$
2017 là một số nguyên dương, do vậy hàm số đã cho xác định khi $\tan 2x$ xác định $\Leftrightarrow 2x\ne \dfrac{\pi }{2}+k\pi ,\,k\in \mathbb{Z}\Leftrightarrow x\ne \dfrac{\pi }{4}+k\dfrac{\pi }{2},\,k\in \mathbb{Z}$.
Câu 6.
Tập xác định của hàm số $y=2016{{\cot }^{2017}}2x$ là
[A]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi \left| k\in \mathbb{Z} \right. \right\}\].
[B]. \[D=\mathbb{R}\backslash \left\{ k\dfrac{\pi }{2}\left| k\in \mathbb{Z} \right. \right\}\].
[C]. \[D=\mathbb{R}\].
[D]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k\dfrac{\pi }{2}\left| k\in \mathbb{Z} \right. \right\}\].
Chọn B.
Tương tự như ví dụ 5, ta có hàm số xác định khi $\cot 2x$ xác định
$\Leftrightarrow 2x\ne k\pi \Leftrightarrow x\ne k\dfrac{\pi }{2},\,k\in \mathbb{Z}$.
Câu 7.
Tập xác định của hàm số $y=\sqrt{1-\cos 2017x}$ là
[A]. \[D=\mathbb{R}\backslash \left\{ k\pi \left| k\in \mathbb{Z} \right. \right\}\].
[B]. \[D=\mathbb{R}\].
[C]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k\pi ;\,\dfrac{\pi }{2}+k\pi \left| k\in \mathbb{Z} \right. \right\}\].
[D]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi \left| k\in \mathbb{Z} \right. \right\}\].
Chọn B.
Hàm số $y=\sqrt{1-\cos 2017x}$ xác định khi $1-\cos 2017x\ge 0.$
Mặt khác ta có $-1\le \cos 2017x\le 1$ nên $1-\cos 2017x\ge 0,\,\forall x\in \mathbb{R}$.
Câu 8.
Tập xác định của hàm số\[y=\dfrac{2}{\sqrt{2-\sin 6x}}\] là
[A]. \[D=\mathbb{R}\backslash \left\{ k\pi |k\in \mathbb{Z} \right\}\].
[B]. \[D=\mathbb{R}\].
[C]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k\pi |k\in \mathbb{Z} \right\}\].
[D]. \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k2\pi |k\in \mathbb{Z} \right\}\].
Chọn B.
Ta có \[\sin 6x<2\]\[\Leftrightarrow 2-\sin 6x>0\],\[\forall x\in \mathbb{R}\]. Vậy hàm số đã cho xác đinh với mọi \[x\in \mathbb{R}\].
Câu 9.
Để tìm tập xác định của hàm số \[y=\tan x+\cos x\], một học sinh đã giải theo các bước sau:
Bước 1: Điều kiện để hàm số có nghĩa là
\[\left\{ \begin{align}
& \sin x\ne 0 \\
& \cos x\ne 0 \\
\end{align} \right.\].
Bước 2: \[\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi \\
& x\ne k\pi \\
\end{align} \right.;\left( k\in \mathbb{Z} \right)\].
Bước 3: Vậy tập xác định của hàm số đã cho là \[D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ;k\pi |k\in \mathbb{Z} \right\}\].
Bài giải của bạn đó đúng chưa? Nếu sai, thì sai bắt đầu ở bước nào?
[A]. Bài giải đúng.
[B]. Sai từ bước 1.
[C]. Sai từ bước 2.
[D]. Sai từ bước 3.
Chọn B.
Nhận thấy hàm số đã cho xác định khi \[\tan x\] xác định (do \[\cos x\] xác định với mọi \[x\in \mathbb{R}\]).
Do vậy hàm số xác định khi \[\cos x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}\].
Câu 10.
Hàm số \[y=\dfrac{1}{\sqrt{\sin x+1}}\] xác định khi và chỉ khi
[A]. \[x\in \mathbb{R}\backslash \left\{ -\dfrac{\pi }{2}+k2\pi |k\in \mathbb{Z} \right\}\].
[B]. \[x\in \mathbb{R}\].
[C]. \[x=-\dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}\].
[D]. \[x=-\dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\].
Chọn A.
Hàm số đã cho xác định \[\Leftrightarrow \sin x+1>0\Leftrightarrow \sin x>-1\Leftrightarrow \sin x\ne -1\] (do \[\sin x\ge -1,\forall x\in \mathbb{R}\])\[\Leftrightarrow x\ne -\dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\].
Dạng chứa tham số trong bài toán liên quan đến tập xác định của hàm sô lượng giác.
Với \[S\subset {{D}_{f}}\] (là tập xác định của hàm số \[f\left( x \right)\]) thì
\[*\text{ }f\left( x \right)\le m,\forall x\in S\Leftrightarrow \underset{S}{\mathop{\max }}\,f\left( x \right)\le m\]. \[*\text{ }f\left( x \right)\ge m,\forall x\in S\Leftrightarrow \underset{S}{\mathop{\min }}\,f\left( x \right)\ge m\].
\[*\text{ }\exists {{x}_{0}}\in S,f\left( {{x}_{0}} \right)\le m\Leftrightarrow \underset{S}{\mathop{\min }}\,f\left( x \right)\le m\] \[*\text{ }\exists {{x}_{0}}\in S,f\left( {{x}_{0}} \right)\ge m\Leftrightarrow \underset{S}{\mathop{\max }}\,f\left( x \right)\ge m\].
Câu 11.
Cho hàm số \[h\left( x \right)=\sqrt{{{\sin }^{4}}x+{{\cos }^{4}}x-2m\sin x.\cos x}\].Tất cả các giá trị của tham số \[m\] để hàm số xác định với mọi số thực \[x\](trên toàn trục số) là
[A]. \[-\dfrac{1}{2}\le m\le \dfrac{1}{2}\].
[B]. \[0\le m\le \dfrac{1}{2}\].
[C]. \[-\dfrac{1}{2}\le m\le 0\].
[D]. \[m\le \dfrac{1}{2}\].
Chọn A.
Xét hàm số \[g\left( x \right)={{\left( {{\sin }^{2}}x \right)}^{2}}+{{\left( {{\cos }^{2}}x \right)}^{2}}-m\sin 2x\]
\[={{\left( {{\sin }^{2}}x+{{\cos }^{2}}x \right)}^{2}}-2{{\sin }^{2}}x{{\cos }^{2}}x-m\sin 2x\]
\[=1-\dfrac{1}{2}{{\sin }^{2}}2x-m\sin 2x\].
Đặt \[t=\sin 2x\]\[\Rightarrow t\in \left[ -1;1 \right]\].
Hàm số \[h\left( x \right)\] xác định với mọi \[x\in \mathbb{R}\]\[\Leftrightarrow g\left( x \right)\ge 0,\forall x\in \mathbb{R}\]\[\Leftrightarrow -\dfrac{1}{2}{{t}^{2}}-mt+1\ge 0,\forall t\in \left[ -1;1 \right]\]
\[\Leftrightarrow {{t}^{2}}+2mt-2\le 0,\forall t\in \left[ -1;1 \right]\].
Đặt \[f\left( t \right)={{t}^{2}}+2mt-2\] trên \[\left[ -1;1 \right]\].
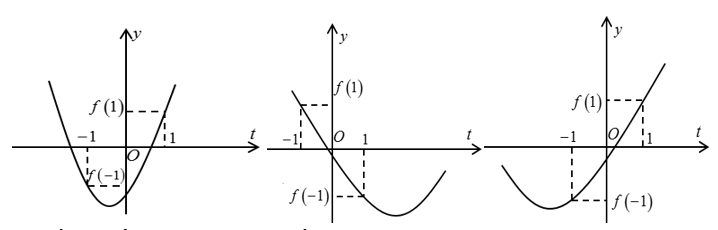
Đồ thị hàm số có thể là một trong ba đồ thị trên.
Ta thấy \[\underset{\left[ -1;1 \right]}{\mathop{\max }}\,f\left( t \right)=f\left( 1 \right)\] hoặc \[\underset{\left[ -1;1 \right]}{\mathop{\max }}\,f\left( t \right)=f\left( -1 \right)\]
Ycbt \[f\left( t \right)={{t}^{2}}+2mt-2\le 0,\forall t\in \left[ -1;1 \right]\Leftrightarrow \underset{\left[ -1;1 \right]}{\mathop{\max }}\,f\left( t \right)\le 0\]
\[\Leftrightarrow \left[ \begin{align}
& f\left( 1 \right)\le 0 \\
& f\left( -1 \right)\le 0 \\
\end{align} \right.\]
\[\Leftrightarrow \left[ \begin{align}
& -1+2m\le 0 \\
& -1-2m\le 0 \\
\end{align} \right.\Leftrightarrow -\dfrac{1}{2}\le m\le \dfrac{1}{2}\].
Câu 12.
Tìm \[m\] để hàm số \[y=\dfrac{3x}{\sqrt{2{{\sin }^{2}}x-m\sin x+1}}\] xác định trên \[\mathbb{R}\].
[A]. \[m\in \left[ -2\sqrt{2};2\sqrt{2} \right]\].
[B]. \[m\in \left( -2\sqrt{2};2\sqrt{2} \right)\].
[C]. \[m\in \left( -\infty ;-2\sqrt{2} \right)\cup \left( 2\sqrt{2};+\infty \right)\].
[D]. \[m\in \left\{ -2\sqrt{2};2\sqrt{2} \right\}\].
Chọn B.
Hàm số xác định trên \[\mathbb{R}\] khi và chỉ khi \[2{{\sin }^{2}}x-m\sin x+1>0,\forall x\in \mathbb{R}\].
Đặt \[t=\sin x\]\[\Rightarrow t\in \left[ -1;1 \right]\]
Lúc này ta đi tìm điều kiện của \[m\] để \[f\left( t \right)=2{{t}^{2}}-mt+1>0,\forall t\in \left[ -1;1 \right]\]
Ta có \[{{\Delta }_{t}}={{m}^{2}}-8\]
TH 1: \[{{\Delta }_{t}}<0\Leftrightarrow {{m}^{2}}-8<0\]\[\Leftrightarrow -2\sqrt{2}<m<2\sqrt{2}\]. Khi đó \[f\left( t \right)>0,\forall t\] (thỏa mãn).
TH 2: \[{{\Delta }_{t}}=0\Leftrightarrow {{m}^{2}}-8=0\]
\[\Leftrightarrow \left[ \begin{align}
& m=-2\sqrt{2} \\
& m=2\sqrt{2} \\
\end{align} \right.\]
(thử lại thì cả hai trường hợp đều không thỏa mãn).
TH 3: \[{{\Delta }_{t}}>0\Leftrightarrow {{m}^{2}}-8>0\]
\[\Leftrightarrow \left[\begin{align}
& m<-2\sqrt{2} \\
& m>2\sqrt{2} \\
\end{align} \right.\]
khi đó tam thức \[f\left( t \right)=2{{t}^{2}}-mt+1\] có hai nghiệm phân biệt \[{{t}_{1}};{{t}_{2}}\left( {{t}_{1}}<{{t}_{2}} \right)\].
Để \[f\left( t \right)>0,\forall t\in \left[ -1;1 \right]\] thì
\[\left[ \begin{align}
& {{t}_{1}}\ge 1\Leftrightarrow \dfrac{m-\sqrt{{{m}^{2}}-8}}{4}\ge 1\Leftrightarrow \sqrt{{{m}^{2}}-8}\ge m-4\left( VN \right) \\
& {{t}_{2}}\le -1\Leftrightarrow \dfrac{m+\sqrt{{{m}^{2}}-8}}{4}\le -1\Leftrightarrow \sqrt{{{m}^{2}}-8}\le -m-4\left( VN \right) \\
\end{align} \right.\]
Vậy \[m\in \left( -2\sqrt{2};2\sqrt{2} \right)\] thỏa mãn yêu cầu bài toán.
Chú ý: Với các bài toán dạng này ta cần chia ba trường hợp để tìm đủ các giá trị của \[m\].
Ở bài toán trên trong TH3 đã áp dụng quy tắc xét dấu tam thức bậc hai “trong trái ngoài cùng”. Tức là trong khoảng hai nghiệm thì cùng dấu với hệ số \[a\], còn khoảng hai nghiệm thì trái dấu với hệ số \[a\].
BÀI TẬP TỰ LUYỆN: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC
Câu 13.
Tìm tập xác định của hàm số $y=\dfrac{1+\cos x}{\sin x}.$
[A]. $D=R\backslash \left\{ k\pi |k\in Z \right\}$.
[B]. $D=R\backslash \left\{ \pi +k\pi |k\in Z \right\}$.
[C]. $D=R\backslash \left\{ \pi +k2\pi |k\in Z \right\}$.
[D]. $D=R\backslash \left\{ k2\pi |k\in Z \right\}$.
Đáp án A.
Hàm số đã cho xác định khi
$\sin x\ne 0\Leftrightarrow \left\{ \begin{align}
& x\ne k2\pi \\
& x\ne \pi +k2\pi \\
\end{align} \right.,k\in \mathbb{Z}$
Nếu giải đến đây ta có thể dễ dàng loại B,C,D vì:
Với C thì thiếu $x\ne \pi +k2\pi ,k\in \mathbb{Z}$
Với B,D thì không thõa mãn.
Với A ta kết hợp gộp nghiệm thì ta được $x\ne k\pi ,k\in \mathbb{Z}$
Câu 14.
Tập xác định của hàm số $y=\sin 5x+\tan 2x$ là:
[A]. $R\backslash \left\{ \dfrac{\pi }{2}+k\pi \right\},k\in Z.$
[B]. $R\backslash \left\{ \dfrac{\pi }{4}+\dfrac{k\pi }{2} \right\},k\in Z.$
[C]. $R\backslash \left\{ \dfrac{\pi }{2}\left( k+1 \right) \right\},k\in Z.$
[D]. $R.$
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \cos x\ne 0 \\
& {{\sin }^{3}}x\ne 1
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \\
& \sin x\ne 1
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \\
& x\ne \dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}
\end{align} \right.$$\Rightarrow D=\mathbb{R}\backslash \left\{ x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}$
Câu 15.
Tập xác định $D$ của hàm số $y=\tan x-\dfrac{1-{{\cos }^{3}}x}{1-{{\sin }^{3}}x}$ là
[A]. $R\backslash \left\{ \dfrac{\pi }{2}+k2\pi |k\in Z \right\}.$
[B]. $R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[C]. $R\backslash \left\{ \dfrac{\pi }{2}+\dfrac{k\pi }{2}|k\in Z \right\}.$
[D]. $R\backslash \left\{ \dfrac{k\pi }{2}|k\in Z \right\}.$
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \cos x\ne 0 \\
& {{\sin }^{3}}x\ne 1 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \\
& \sin x\ne 1 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \\
& x\ne \dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \\
\end{align} \right.$$\Rightarrow D=\mathbb{R}\backslash \left\{ x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}$
Câu 16.
Tập xác định của hàm số $y=\tan \left( 2x+\dfrac{\pi }{3} \right)$ là
[A]. $R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[B]. $R\backslash \left\{ \dfrac{\pi }{6}+k\pi |k\in Z \right\}.$
[C]. $R\backslash \left\{ \dfrac{\pi }{12}+k\pi |k\in Z \right\}.$
[D]. $R\backslash \left\{ \dfrac{\pi }{12}+\dfrac{k\pi }{2}|k\in Z \right\}.$
Đáp án D.
Hàm số đã cho xác định khi
$\cos \left( 2x+\dfrac{\pi }{3} \right)\ne 0\Leftrightarrow 2x+\dfrac{\pi }{3}\ne \dfrac{\pi }{2}+k\pi \Leftrightarrow x\ne \dfrac{\pi }{12}+\dfrac{k\pi }{2},k\in \mathbb{Z}\Rightarrow D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{12}+\dfrac{k\pi }{2},k\in \mathbb{Z} \right\}$
Câu 17.
Xét bốn mệnh đề sau
- Hàm số $y=\sin x$ có tập xác định là $R.$
- Hàm số $y=\cos x$ có tập xác định là $R.$
- Hàm số $y=\tan x$ có tập xác định là $R\backslash \left\{ k\pi |k\in Z \right\}.$
- Hàm số $y=\cot x$ có tập xác định là $R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.$
Số mệnh đề đúng là
[A]. 1.
[B]. 2.
[C]. 3.
[D]. 4.
Đáp án B.
Mệnh đề $\left( 1 \right)$ và $\left( 2 \right)$là đúng
Mệnh đề $\left( 3 \right)$ và $\left( 4 \right)$là sai
Sửa lại cho đúng như sau
$\left( 3 \right)$Hàm số $y=\tan x$ có TXĐ là $\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}$
$\left( 4 \right)$Hàm số $y=\tan x$ có TXĐ là $\mathbb{R}\backslash \left\{ k\pi ,k\in \mathbb{Z} \right\}$
Câu 18.
Tập xác định của hàm số $y=\cos \sqrt{x}$ là
[A]. $D=\left[ 0;2\pi \right].$
[B]. $D=\left[ 0;+\infty \right).$
[C]. $D=R.$
[D]. $D=R\backslash \left\{ 0 \right\}.$
Đáp án B.
Hàm số đã cho xác định khi $x\ge 0$
Câu 19.
Tập xác định của hàm số $y=\dfrac{1}{\sin x}-\dfrac{1}{\cos x}$ là
[A]. $R\backslash \left\{ k\pi |k\in Z \right\}.$
[B]. $R\backslash \left\{ k2\pi |k\in Z \right\}.$
[C]. $R\backslash \left\{ -\dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[D]. $R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.$
Đáp án D.
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \sin x\ne 0 \\
& \cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne k\pi \\
& x\ne \dfrac{\pi }{2}+k\pi \\
\end{align} \right.$$\Leftrightarrow x\ne \dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 20.
Tìm tập xác định của hàm số $y=3\tan x+2\cot x+x.$
[A]. $D=R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[B]. $D=R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.$
[C]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\dfrac{\pi }{2}|k\in Z \right\}.$
[D]. $D=R.$
Đáp án B.
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \sin x\ne 0 \\
& \cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne k\pi \\
& x\ne \dfrac{\pi }{2}+k\pi \\
\end{align} \right.$$\Leftrightarrow x\ne \dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 21.
Tìm tập xác định của hàm số $y=\dfrac{1}{{{\sin }^{2}}x-{{\cos }^{2}}x}.$
[A]. $R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[B]. $R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.$
[C]. $R.$
[D]. $R\backslash \left\{ \dfrac{\pi }{4}+k\dfrac{\pi }{2}|k\in Z \right\}.$
Đáp án D.
Hàm số đã cho xác định khi ${{\sin }^{2}}x-{{\cos }^{2}}x\ne 0\Leftrightarrow \cos 2x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{4}+\dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 22.
Tìm tập xác định của hàm số $y=\dfrac{2017\tan 2x}{{{\sin }^{2}}x-{{\cos }^{2}}x}.$
[A]. $R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[B]. $R\backslash \left\{ \dfrac{\pi }{2} \right\}.$
[C]. $R.$
[D]. $R\backslash \left\{ \dfrac{\pi }{4}+k\dfrac{\pi }{2}|k\in Z \right\}.$
Đáp án D.
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& {{\sin }^{2}}x-{{\cos }^{2}}x\ne 0 \\
& \cos 2x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \cos 2x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{4}+\dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 23.
Tập xác định của hàm số $y=\dfrac{\sin x}{\sin x+\cos x}.$
[A]. $D=R\backslash \left\{ -\dfrac{\pi }{4}+k\pi |k\in Z \right\}.$
[B]. $D=R\backslash \left\{ k\dfrac{\pi }{4}|k\in Z \right\}.$
[C]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[D]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi |k\in Z \right\}.$
Đáp án A.
Hàm số đã cho xác định khi $\sin x+\cos x\ne 0\Leftrightarrow \sqrt{2}sin\left( x+\dfrac{\pi }{4} \right)\ne 0\Leftrightarrow sin\left( x+\dfrac{\pi }{4} \right)\ne 0\Leftrightarrow x\ne \dfrac{-\pi }{4}+k\pi ,k\in \mathbb{Z}$
Vậy TXĐ $D=\mathbb{R}\backslash \left\{ \dfrac{-\pi }{4}+k\pi ,k\in \mathbb{Z} \right\}$
Câu 24.
Tìm tập xác định của hàm số $y=\dfrac{\sin x}{\sin x-\cos x}.$
[A]. $D=R\backslash \left\{ -\dfrac{\pi }{4}+k2\pi |k\in Z \right\}.$
[B]. $D=R\backslash \left\{ k\dfrac{\pi }{4}|k\in Z \right\}.$
[C]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[D]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi |k\in Z \right\}.$
Đáp án D.
Hàm số đã cho xác định khi $\sin x-\cos x\ne 0\Leftrightarrow \sqrt{2}sin\left( x-\dfrac{\pi }{4} \right)\ne 0\Leftrightarrow sin\left( x-\dfrac{\pi }{4} \right)\ne 0\Leftrightarrow x\ne \dfrac{\pi }{4}+k\pi ,k\in \mathbb{Z}$
Vậy TXĐ $D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{4}+k\pi ,k\in \mathbb{Z} \right\}$
Câu 25.
Tập xác định của hàm số $y=\sqrt{\sin 2x+1}$ là
[A]. $D=R\backslash \left\{ k\pi |k\in Z \right\}.$
[B]. $D=R.$
[C]. $D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{2}+k\pi |k\in Z \right\}.$
[D]. $D=R\backslash \left\{ \dfrac{\pi }{2}+k2\pi |k\in Z \right\}.$
Đáp án B.
Ta có $\sin 2x\ge -1,\forall x\in \mathbb{R}\Leftrightarrow \sin 2x+1\ge 0,\forall x\in \mathbb{R}$. Vậy hàm số đã cho xác định với mọi $x\in \mathbb{R}$
Câu 26.
Tìm tập xác định của hàm số \[y=\dfrac{\tan x}{\sqrt{15-14\cos 13x}}.\]
[A]. \[D=R\backslash \left\{ k\pi |k\in Z \right\}.\]
[B]. \[D=R.\]
[C]. \[D=R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.\]
[D]. \[D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi |k\in Z \right\}\].
Đáp án C.
Ta có $\cos 13x\le 1<\dfrac{15}{14}\Rightarrow 15-14cos13x>0$.
Vậy hàm số đã cho xác định khi $\cos x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}$
Câu 27.
Tìm tập xác định của hàm số: \[y=\dfrac{\cot 2x}{\sqrt{2017-2016\sin 2015x}}.\]
[A]. . \[D=R\backslash \left\{ k\pi |k\in Z \right\}.\]
[B]. \[D=R.\] .
[C]. \[D=R\backslash \left\{ \dfrac{\pi }{2}+k\pi |k\in Z \right\}.\]
[D]. \[D=R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.\]
Đáp án D.
Tương tự câu 14, hàm số đã cho xác định khi $\sin 2x\ne 0\Leftrightarrow x\ne \dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 28.
Tìm tập xác định của hàm số: \[y=\sqrt{\dfrac{20+19\cos 18x}{1-\operatorname{sinx}}}\] .
[A]. \[D=R\backslash \left\{ k\pi |k\in Z \right\}.\]
[B]. \[D=R\backslash \left\{ k2\pi |k\in Z \right\}.\]
[C]. \[D=R\backslash \left\{ \dfrac{\pi }{2}+k2\pi |k\in Z \right\}.\]
[D]. \[D=R\backslash \left\{ k\dfrac{\pi }{2}|k\in Z \right\}.\]
Đáp án C.
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \dfrac{20+19\cos 18x}{1-\sin x}\ge 0 \\
& 1-\sin x\ne 0 \\
\end{align} \right.$
Mà $19+20\cos 18x>0,\forall x\in \mathbb{R}$ nên hàm số đã cho xác định $1-\sin x>0\Leftrightarrow \sin x\ne 1\Leftrightarrow x\ne \dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$
Vậy hàm số đã cho xác định khi $\cos x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}$
Câu 29.
Hàm số nào sau đây có tập xác định là \[R\]?
[A]. \[y=2\cos \sqrt{x}\] .
[B]. \[y=\cos \dfrac{1}{x}\] .
[C]. \[y=\dfrac{\tan 2x}{{{\sin }^{2}}x+1}\].
[D]. \[y=\sqrt{\dfrac{\sin 2x+3}{\cos 4x+5}}\].
Đáp án D.
Với A thì hàm số xác định khi $x\ge 0$
Với B thì hàm số xác định khi $\tan 2x$xác định $\Leftrightarrow 2x\ne \dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.
Với C thì hàm số xác định khi $x\ne 0$
Với D thì $\dfrac{\sin 2x+3}{\cos 4x+5}>0,\forall x\in \mathbb{R}$
Vậy ta chọn D vì các phương án trên không có phương án nào thỏa mãn hàm số có tập xác định là $\mathbb{R}.$
Câu 30.
Hàm số nào sau đây có tập xác định khác với các hàm số còn lại?
[A]. \[y=\tan x\].
[B]. \[y=\dfrac{\sin x+\cos x}{\cos x}\] .
[C]. \[y=\dfrac{\tan 2017x+2018}{\cos x}\].
[D]. \[y=\sqrt{\dfrac{1}{1-{{\sin }^{2}}x}}\] .
Đáp án C.
Với A thì hàm số xác định khi $\cos x\ne 0$
Với B thì hàm số xác định khi $\cos x\ne 0$
Với C thì hàm số xác định khi
$\left\{ \begin{align}
& \cos x\ne 0 \\
& \cos 2017x\ne 0 \\
\end{align} \right.$
Từ đây ta chọn C do khác với A và B
Câu 31.
Hàm số \[y=\sqrt{\cos x-1}+1-{{\cos }^{2}}x\] chỉ xác định khi:
[A]. \[x\ne \dfrac{\pi }{2}+k\pi ,k\in Z\].
[B]. \[x=0\].
[C]. \[x\ne k\pi ,k\in Z\].
[D]. \[x=k2\pi ,k\in Z\].
Đáp án D.
Hàm số đã cho xác định khi $\cos x-1\ge 0$, mà $\cos x-1\le 0,\forall x\in \mathbb{R}$, do vậy để hàm số xác định thì $\cos x=1\Leftrightarrow x=k2\pi ,k\in \mathbb{Z}$
Câu 32.
Hàm số \[y=\sqrt{1-\sin 2x}-\sqrt{1+\sin 2x}\] có tập xác định là:
[A]. \[\varnothing \] .
[B]. \[R\].
[C]. \[\left[ \dfrac{\pi }{6}+k2\pi ;\dfrac{\pi }{3}+k2\pi \right],k\in Z\].
[D]. \[\left[ \dfrac{5\pi }{6}+k2\pi ;\dfrac{13\pi }{6}+k2\pi \right],k\in Z\] .
Đáp án B.
Cách 1: Hàm số đã cho xác định khi
$\left\{ \begin{align}
& 1-\sin 2x\ge 0 \\
& 1+\sin 2x\ge 0 \\
\end{align} \right.$$\Leftrightarrow -1\le \sin 2x\le 1$ đúng với mọi $x\in \mathbb{R}$
Cách 2: $y=\left| \sin x-\cos x \right|-\left| \sin x+\cos x \right|$,tập xác định là $\mathbb{R}$
Câu 33.
Chọn khẳng định đúng:
[A]. Hàm số \[y=\sqrt{\sin x}\]có tập xác định là các đoạn \[\left[ -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right],k\in Z\] .
[B]. Hàm số \[y=\sqrt{\cos x}\]có tập xác định là các đoạn \[\left[ k2\pi ;\pi +k2\pi \right],k\in Z\].
[C]. Hàm số \[y=\sqrt{\sin x}+\sqrt{\cos x}\]có tập xác định là các đoạn \[\left[ k2\pi ;\dfrac{\pi }{2}+k2\pi \right],k\in Z\].
[D]. Hàm số \[y=\dfrac{1}{\sqrt{\sin x}}\]có tập xác định là các đoạn \[\left[ k2\pi ;\dfrac{\pi }{2}+k2\pi \right],k\in Z\].
Đáp án C.
Với A thì hàm số $y=\sqrt{\sin x}$ xác định khi $\sin x\ge 0\Leftrightarrow k2\pi \le x\le \pi +k2\pi ,k\in \mathbb{Z}$. vậy A sai.
Với B thì hàm số$y=\sqrt{\cos x}$ xác định khi $\cos x\ge 0\Leftrightarrow \dfrac{-\pi }{2}+k2\pi \le x\le \dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$$\cos x\ne 0$
Với C thì hàm số xác định khi $y=\sqrt{\cos x}+\sqrt{\sin x}$ xác định khi
$\left\{ \begin{align}
& \cos x\ge 0 \\
& \sin x\ge 0 \\
\end{align} \right.$$\Leftrightarrow k2\pi \le x\le \dfrac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$.
Vậy C đúng.
Câu 34.
Xét hai mệnh đề:
(I): Các hàm số \[y=\dfrac{1}{\sin x}\] và \[y=\cot x\]có chung tập xác định là \[R\backslash \left\{ x|x=k\pi ,k\in Z \right\}\].
(II): Các hàm số \[y=\dfrac{1}{\cos x}\] và \[y=\tan x\] có chung tập xác định là \[R\backslash \left\{ x|x=\dfrac{\pi }{2}+k\pi ,k\in Z \right\}\].
[A]. Chỉ (I) đúng.
[B]. Chỉ (II) đúng.
[C]. Cả hai đều sai .
[D]. Cả hai đều đúng.
Đáp án D.
Ta thấy cả hai hàm số $y=\dfrac{1}{\sin x}$ và $y=\cot x$đều xác định khi $\sin x\ne 0$. tương tự thì hai hàm số ở mệnh đề II đều xác định khi $\cos x\ne 0$.
Câu 35.
Cho hàm số \[y=f(x)=\sqrt{\sin x}-\sqrt{\cos x}\] với \[0\le x\le 2\pi \]. Tập xác định của hàm số là:
[A]. \[\left[ 0;\pi \right]\] .
[B]. \[\left[ \dfrac{\pi }{2};\dfrac{3\pi }{2} \right]\] .
[C]. \[\left[ 0;\dfrac{\pi }{2} \right]\] .
[D]. \[\left( 0;\dfrac{\pi }{2} \right)\] .
Đáp án C.
Hàm số xác định khi
$\left\{ \begin{align}
& x\in \left[ 0;2\pi \right] \\
& \sin x\ge 0 \\
& \cos x\ge 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& 0\le x\le 2\pi \\
& 0\le x\le \pi \\
& \dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2} \\
\end{align} \right.$$\Leftrightarrow 0\le x\le \dfrac{\pi }{2}$
Câu 36.
Cho hàm số \[y=f(x)=\dfrac{\tan x+1}{\tan x-1},\left( 0<x<\pi \right)\]. Tập xác định:
[A]. \[\left( 0;\dfrac{\pi }{2} \right)\].
[B]. \[\left( \dfrac{\pi }{2};\pi \right)\] .
[C]. \[\left( 0;\pi \right)\backslash \left\{ \dfrac{\pi }{2} \right\}\] .
[D]. \[\left( 0;\pi \right)\backslash \left\{ \dfrac{\pi }{4};\dfrac{\pi }{2} \right\}\].
Đáp án D.
Hàm số xác định khi
$\left\{ \begin{align}
& 0<x<\pi \\
& \cos x\ne 0 \\
& \tan x\ne 1 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& 0<x<\pi \\
& x\ne \dfrac{\pi }{2} \\
& x\ne \dfrac{\pi }{4} \\
\end{align} \right.$$\Leftrightarrow x\in \left( 0;\pi \right)\backslash \left\{ \dfrac{\pi }{4};\dfrac{\pi }{2} \right\}$
Câu 37.
Tập xác định của hàm số \[y=3{{\tan }^{2}}\left( \dfrac{x}{2}-\dfrac{\pi }{4} \right)\] là:
[A]. \[R\] .
[B]. \[R\backslash \left\{ \dfrac{\pi }{2}+k\pi ,k\in Z \right\}\].
[C]. \[R\backslash \left\{ \dfrac{3\pi }{2}+k2\pi ,k\in Z \right\}\] .
[D]. \[R\backslash \left\{ \dfrac{\pi }{2}+k2\pi ,k\in Z \right\}\].
Đáp án C.
Hàm số xác định khi $\cos \left( \dfrac{x}{2}-\dfrac{\pi }{4} \right)\ne 0\Leftrightarrow x\ne \dfrac{3\pi }{2}+k2\pi ,k\in \mathbb{Z}$
Câu 38.
Tập xác định của hàm số \[y=2\cot \left( 2x-\dfrac{\pi }{3} \right)\] là:
[A]. \[R\backslash \left\{ \dfrac{2\pi }{3}+\dfrac{k\pi }{2},k\in Z \right\}\] .
[B]. \[R\backslash \left\{ \dfrac{\pi }{6}+k\pi ,k\in Z \right\}\].
[C]. \[R\backslash \left\{ \dfrac{\pi }{6}+k2\pi ,k\in Z \right\}\] .
[D]. \[R\backslash \left\{ \dfrac{5\pi }{12}+\dfrac{k\pi }{2},k\in Z \right\}\].
Đáp án A.
Hàm số xác định khi $\sin \left( 2x-\dfrac{\pi }{3} \right)\ne 0\Leftrightarrow x\ne \dfrac{2\pi }{3}+\dfrac{k\pi }{2},k\in \mathbb{Z}$
Câu 39.
Cho hàm số \[y=\dfrac{\cos 2x}{1+\tan x}\]. Hãy chỉ ra khoảng mà hàm số không xác định \[(k\in Z)\]
[A]. \[\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{4}+k2\pi \right)\].
[B]. \[\left( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right)\].
[C]. \[\left( \dfrac{3\pi }{4}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)\] .
[D]. \[\left( \pi +k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)\] .
Đáp án B.
Hàm số đã cho xác định khi
$\left\{ \begin{align}
& \cos x\ne 0 \\
& \tan x\ne -1 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi \\
& x\ne \dfrac{-\pi }{4}+k\pi \\
\end{align} \right.,k\in \mathbb{Z}$
Khoảng $\left( \dfrac{-\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right)$ chứa $x=\dfrac{-\pi }{4}+k2\pi $ nên hàm số không xác định trong khoảng này
Câu 40.
Xét hai câu sau:
(I): Các hàm số \[y=\sin x\] và \[y=\operatorname{cosx}\]có chung tập xác định là \[R.\]
(II): Các hàm số \[y=\tan x\] và \[y=\cot x\] có chung tập xác định là \[R\backslash \left\{ \left\{ x|x=\dfrac{\pi }{2}+k\pi \right\}\cup \left\{ x|x=k\pi \right\} \right\},k\in Z\].
[A]. Chỉ (I) đúng.
[B]. Chỉ (II) đúng.
[C]. Cả hai đều sai .
[D]. Cả hai đều đúng.
Đáp án A.
Hàm số $y=\tan x$ tập xác định là $\mathbb{R}\backslash \left\{ x/x=\dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}$, Hàm số $y=\cot x$ tập xác định là $\mathbb{R}\backslash \left\{ x/x=k\pi ,k\in \mathbb{Z} \right\}$, suy ra (II) sai
Câu 41.
Tập xác định của hàm số \[y=\dfrac{\cos 3x}{\cos x.cos\left( x-\dfrac{\pi }{3} \right).cos\left( \dfrac{\pi }{3}+x \right)}\] là:
[A]. \[R\backslash \left\{ \dfrac{\pi }{6}+\dfrac{k\pi }{3};\dfrac{5\pi }{6}+k\pi ;\dfrac{\pi }{6}+k\pi ,k\in Z \right\}\] .
[B]. \[R\backslash \left\{ \dfrac{5\pi }{6}+k\pi ;\dfrac{\pi }{6}+k\pi ,k\in Z \right\}\].
[C]. \[R\backslash \left\{ \dfrac{\pi }{2}+k\pi ;\dfrac{5\pi }{6}+k\pi ;\dfrac{\pi }{6}+k\pi ,k\in Z \right\}\].
[D]. \[R\backslash \left\{ \dfrac{\pi }{2}+k\pi ;\dfrac{5\pi }{6}+\dfrac{k\pi }{2},k\in Z \right\}\].
Đáp án A.
Hàm số đã cho xác định khi $\cos 3x.\cos \left( x-\dfrac{\pi }{3} \right).\cos \left( x+\dfrac{\pi }{3} \right)\ne 0$
\[\Leftrightarrow \left[ \begin{align}
& \cos 3x\ne 0\Leftrightarrow x\ne \dfrac{\pi }{6}+\dfrac{k\pi }{3} \\
& \cos \left( x-\dfrac{\pi }{3} \right)\ne 0\Leftrightarrow x-\dfrac{\pi }{3}\ne \dfrac{\pi }{2}+k\pi \\
& \cos \left( \dfrac{\pi }{3}+x \right)\ne 0\Leftrightarrow \dfrac{\pi }{3}+x\ne \dfrac{\pi }{2}+k\pi \\
\end{align} \right.\]\[\Leftrightarrow \left[ \begin{align}
& x\ne \dfrac{\pi }{6}+\dfrac{k\pi }{3} \\
& x\ne \dfrac{5\pi }{6}+k\pi ,k\in Z \\
& x\ne \dfrac{\pi }{6}+k\pi \\
\end{align} \right.\]
Câu 42.
Tập xác định của hàm số \[f(x)=\dfrac{5\sin 2x+3}{12\operatorname{sinx}}+\dfrac{\sqrt{{{\cos }^{2}}x}+5}{\cos x}\] là:
[A]. \[D=R\backslash \left\{ k2\pi |k\in Z \right\}\].
[B]. \[D=R\backslash \left\{ \dfrac{k\pi }{2}|k\in Z \right\}\] .
[C]. \[D=R\backslash \left\{ k\pi |k\in Z \right\}\].
[D]. \[D=R\backslash \left\{ -\dfrac{\pi }{2}+k\pi |k\in Z \right\}\].
Đáp án B.
Hàm số $f\left( x \right)=\dfrac{5\sin 2x+3}{12\sin x}+\dfrac{\sqrt{{{\cos }^{2}}x}+5}{\cos x}$ xác định khi
$\left\{ \begin{align}
& \sin x\ne 0 \\
& \cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{2}+k\pi \\
& x\ne k\pi \\
\end{align} \right.;k\in Z\Leftrightarrow x\ne \dfrac{k\pi }{2},k\in Z$.
Câu 43.
Tập xác định của hàm số \[\dfrac{1-\cos x}{2\sin x+1}\] là:
[A]. \[D=R\backslash \left\{ -\dfrac{\pi }{6}+k2\pi ;\dfrac{7\pi }{6}+k2\pi |k\in Z \right\}\].
[B]. \[D=R\backslash \left\{ \dfrac{7\pi }{6}+k\pi |k\in Z \right\}\] .
[C]. \[D=R\backslash \left\{ -\dfrac{\pi }{6}+k\pi |k\in Z \right\}\] .
[D]. \[D=R\backslash \left\{ -\dfrac{\pi }{6}+k\pi ;\dfrac{7\pi }{6}+k\pi |k\in Z \right\}\] .
Đáp án A.
ĐK: $2\sin x+1=0\Leftrightarrow \sin x\ne -\dfrac{1}{2}\ne \left\{ \begin{align}
& x\ne -\dfrac{\pi }{6}+k2\pi \\
& x\ne \dfrac{7\pi }{6}+k2\pi \\
\end{align} \right.$
Tập xác định \[D=\mathbb{R}\backslash \left\{ -\dfrac{\pi }{6}+k2\pi ;\dfrac{7\pi }{6}+k2\pi |k\in Z \right\}\].
Câu 44.
Tập xác định của hàm số \[\sqrt{\dfrac{5-3\cos 2x}{\left| 1+\sin \left( 2x-\dfrac{\pi }{2} \right) \right|}}\] là:
[A]. \[D=R\backslash \left\{ k\pi |k\in Z \right\}\] .
[B]. \[D=R\] .
[C]. \[D=R\backslash \left\{ \dfrac{k\pi }{2}|k\in Z \right\}\].
[D]. \[D=R\backslash \left\{ k2\pi |k\in Z \right\}\].
Đáp án A.
Ta có $-1\le \cos 2x\le 1$ nên $5-3\cos 2x>0,\forall x\in \mathbb{R}$.
Mặt khác $\left| 1+\sin \left( 2x-\dfrac{\pi }{2} \right) \right|\ge 0$.
Hàm số đã cho xác định $\Leftrightarrow 1+\sin \left( 2x-\dfrac{\pi }{2} \right)\ne 0$
\[\Leftrightarrow \sin \left( 2x-\dfrac{\pi }{2} \right)\ne -1\Leftrightarrow 2x-\dfrac{\pi }{2}\ne -\dfrac{\pi }{2}+k2\pi \Leftrightarrow x\ne k\pi ,k\in Z.\]
Tập xác định $D=\mathbb{R}\backslash \left\{ k\pi ,k\in Z \right\}$.
Câu 45.
Tập xác định của hàm số \[y=\cot \left( x+\dfrac{\pi }{6} \right)+\sqrt{\dfrac{1+\cos x}{1-\cos x}}\] là:
[A]. \[D=R\backslash \left\{ -\dfrac{\pi }{6}+k2\pi |k\in Z \right\}\] .
[B]. \[D=R\backslash \left\{ \dfrac{7\pi }{6}+k\pi ,k2\pi |k\in Z \right\}\].
[C]. \[D=R\backslash \left\{ k2\pi |k\in Z \right\}\].
[D]. \[D=R\backslash \left\{ -\dfrac{\pi }{6}+k\pi |k\in Z \right\}\].
Đáp án B.
Vì $-1\le \cos x\le 1$ nên $1+\cos x\ge 0$ và $1-\cos x\ge 0\Rightarrow \dfrac{1+\cos x}{1-\cos x}\ge 0$.
Hàm số xác định
$\Leftrightarrow \left\{ \begin{align}
& \sin \left( x+\dfrac{\pi }{6} \right)\ne 0 \\
& 1-\cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x+\dfrac{\pi }{6}\ne k\pi \\
& x\ne k2\pi \\
\end{align} \right.,k\in Z$.
Tập xác định của hàm số là $\mathbb{R}\backslash \left\{ -\dfrac{\pi }{6}+k\pi ,k2\pi |k\in Z \right\}$.
Câu 46.
Tập xác định của hàm số \[y=\sqrt{2+\sin x}-\dfrac{1}{{{\tan }^{2}}x-1}\] là:
[A]. \[D=R\backslash \left\{ \pm \dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{2}+k\pi |k\in Z \right\}\]
[B]. \[D=R\backslash \left\{ \dfrac{k\pi }{2}|k\in Z \right\}\] .
[C]. \[D=R\backslash \left\{ \dfrac{\pi }{4}+k\pi |k\in Z \right\}\] .
[D]. \[D=R\backslash \left\{ \pm \dfrac{\pi }{4}+k\pi |k\in Z \right\}\].
Đáp án A.
Vì $-1\le \sin x\le 1$ neen $2+\sin x\ge 0,\forall x\in \mathbb{R}$.
Hàm số xác định
$\Leftrightarrow \left\{ \begin{align}
& 2+\sin x\ge 0 \\
& {{\tan }^{2}}x-1\ne 0 \\
& \cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& \tan x\ne \pm 1 \\
& \cos x\ne 0 \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \pm \dfrac{\pi }{4}+k\pi \\
& x\ne \dfrac{\pi }{2}+k\pi \\
\end{align} \right.,k\in Z$
Vậy $D=\mathbb{R}\backslash \left\{ \pm \dfrac{\pi }{4}+k\pi ,\dfrac{\pi }{2}+k\pi ,k\in Z \right\}$.
Câu 47.
Hàm số \[y=\dfrac{1+\tan \left( \dfrac{\pi }{3}+2x \right)}{{{\cot }^{2}}x+1}\] có tập xác định là:
[A]. \[D=R\backslash \left\{ \dfrac{\pi }{6}+k\dfrac{\pi }{2},k\pi |k\in Z \right\}\].
[B]. \[D=R\backslash \left\{ \dfrac{\pi }{12}+k\pi ,k\dfrac{\pi }{2}|k\in Z \right\}\] .
[C]. \[D=R\backslash \left\{ \dfrac{\pi }{12}+k\pi ;k\pi |k\in Z \right\}\] .
[D]. \[D=R\backslash \left\{ \dfrac{\pi }{12}+k\dfrac{\pi }{2};k\pi |k\in Z \right\}\].
Đáp án D.
Hàm số xác định khi
$\left\{ \begin{align}
& {{\cot }^{2}}x+1\ne 0 \\
& \cos \left( \dfrac{\pi }{3}+2x \right)\ne 0 \\
& \sin x\ne 0 \\
\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}
& \dfrac{\pi }{3}+2x\ne \dfrac{\pi }{2}+k\pi \\
& x\ne k\pi \\
\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}
& x\ne \dfrac{\pi }{12}+k\dfrac{\pi }{2} \\
& x\ne k\pi \\
\end{align} \right.,k\in Z$.
Vậy tập xác định của hàm số là $D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{12}+k\dfrac{\pi }{2},k\pi ,k\in Z \right\}$.