Hệ thức lượng trong tam giác, trắc nghiệm toán 10
Câu 1.
Cho $ a=80,\text{ }b=51$ và $ c=113$ . Tính $ C. $
[A]. $ 117,5{}^\circ . $
[B]. $ 27,5{}^\circ . $
[C]. $ 157,4{}^\circ . $
[D]. $ 62,5{}^\circ . $
Hướng dẫn giải:
$ \cos C=\dfrac{a2+b2-c2}{2ab}=\dfrac{{{80}^{2}}+{{51}^{2}}-{{133}^{2}}}{2. 80. 51}=-0,462\Rightarrow C=117,5{}^\circ . $ Chọn đáp án A.
Câu 2.
Cho $ a=2178,\text{ }c=1719$ và $ B=23{}^\circ $ . Tính $ b$ .
[A]. \[2184,9. \]
[B]. \[897,7. \]
[C]. \[80937,8. \]
[D]. \[2062,1. \]
Hướng dẫn giải:
$ {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos B$ $ ={{(2178)}^{2}}+{{(1719)}^{2}}-2\times 2178\times 1719\cos 23{}^\circ $
$ \Rightarrow b=897,7$ . Chọn đáp án B.
Câu 3.
Cho $ a=17,\text{ }b=39,\text{ }c=50$ . Tính góc nhỏ nhất trong tam giác $ ABC$ ?
[A]. $ 106,86{}^\circ . $
[B]. $ 73,12{}^\circ . $
[C]. $ 16,86{}^\circ . $
[D]. $ 163,12{}^\circ . $
Hướng dẫn giải:
Cạnh nhỏ nhất là $ a$ . Suy ra góc nhỏ nhất là $ A$ , ta có :
\[\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=\dfrac{3732}{3900}\Rightarrow A=16,86{}^\circ \]. Chọn đáp án C.
Câu 4.
Cho $ a=117,\text{ }b=230,\text{ }c=185$ . Tính góc lớn nhất trong tam giác $ ABC$ ?
[A]. $ 6,6{}^\circ . $
[B]. $ 96,6{}^\circ . $
[C]. $ 53{}^\circ . $
[D]. $ 37{}^\circ . $
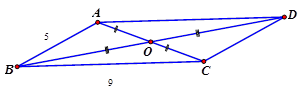
Hướng dẫn giải:
Cạnh $ b$ lớn nhất. Suy ra góc $ \cos B=\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}$ lớn nhất.
$ \cos B=\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}=\dfrac{{{117}^{2}}+{{185}^{2}}-{{230}^{2}}}{2. 117. 185}\Rightarrow B=96,6{}^\circ $ . Chọn đáp án B.
Câu 5.
Cho $ a=12,\text{ }c=21,\text{ }B=72{}^\circ $ . Tính $ C$ ?
[A]. $ 69,2{}^\circ . $
[B]. $ 81,0{}^\circ . $
[C]. $ 33,4{}^\circ . $
[D]. $ 74,6{}^\circ . $
Hướng dẫn giải:
$ {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos B={{12}^{2}}+{{21}^{2}}-2. 12. 21\cos 72{}^\circ \Rightarrow b=20,72$
$ \dfrac{s}{\sin c}=\dfrac{b}{\sin b}\Rightarrow \sin C=\dfrac{c\operatorname{sinB}}{b}=\dfrac{21\sin 72{}^\circ }{20,72}=0,964\Rightarrow C=74,6{}^\circ $ . Chọn đáp án D.
Câu 6.
Cho tam giác $ ABC$ có $ AC=8,\text{ }AB=5,\text{ }\widehat{BAC}=60{}^\circ $ . Khi đó, cạnh $ BC$ bằng:
[A]. $ 7. $
[B].
$ 6. $
[C]. $ \dfrac{49}{6}. $
[D].
$ \dfrac{35}{6}. $
Hướng dẫn giải:
$ B{{C}^{2}}={{a}^{2}}={{c}^{2}}+{{b}^{2}}-2bc\cos A$ $ =25+64-2. 5. 8. \dfrac{1}{2}=49\Rightarrow BC=7$ . Chọn đáp án A.
Câu 7.
Cho tam giác $ ABC$ có$ a=21,\text{ }b=17,\text{ }c=8$ . Góc $ A$ có số đo tính đến đơn vị phút là:
[A]. $ 82{}^\circ 35′. $
[B]. $ 108{}^\circ 53′. $
[C]. $ 105{}^\circ 12′. $
[D]. $ 96{}^\circ 32′. $
Hướng dẫn giải:
$ {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A\Rightarrow \cos A=\dfrac{{{y}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=\dfrac{{{17}^{2}}+{{8}^{2}}-21}{2. 17. 2}$ $ =-\dfrac{11}{34}=108{}^\circ 53’$ . Chọn đáp án B.
Câu 8.
Cho tam giác $ ABC$ có $ A=30{}^\circ ,\text{ }a=20,\text{ }b=20\sqrt{3}$ . Số đo của góc $ B$ là số nào sau đây:
[A]. $ 60{}^\circ . $
[B]. $ 45{}^\circ . $
[C]. $ 90{}^\circ . $
[D]. $ 60{}^\circ $ hoặc $ 120{}^\circ . $
Hướng dẫn giải:
Theo định lý hàm số $ \sin $ ta có :
\[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}\Rightarrow \operatorname{sinB}=\dfrac{b. \sin A}{a}=\dfrac{20\sqrt{3}\times \dfrac{1}{2}}{20}=\dfrac{\sqrt{3}}{2}\Rightarrow \left[ \begin{array}{l}
B=60{}^\circ
\\
B=120{}^\circ
\end{array} \right. \]
. Chọn đáp án D.
Câu 9.
Tam giác $ ABC$ có $ AB=6\text{cm},\text{ }AC=8\text{cm}$ và $ BC=10\text{cm}$ . Độ dài đường trung tuyến xuất phát từ đỉnh $ A$ của tam giác bằng:
[A]. $ 4\text{cm}\text{. }$
[B]. $ \sqrt{3}\text{cm}\text{. }$
[C]. $ 7\text{cm}\text{. }$
[D]. $ 5\text{cm}\text{. }$
Hướng dẫn giải:
Áp dụng công thức đường trung tuyến $ m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}$ ta được: $ m_{a}^{2}=\dfrac{A{{C}^{2}}+A{{B}^{2}}}{2}-\dfrac{B{{C}^{2}}}{4}=\dfrac{{{8}^{2}}+{{6}^{2}}}{2}-\dfrac{{{10}^{2}}}{4}=25$
$ \Rightarrow {{m}_{a}}=5. $
Chọn đáp án D.
Câu 10.
Tam giác $ ABC$ vuông tại $ A$ và có $ AB=AC=a$ . Tính độ dài đường trung tuyến $ BM$ của tam giác đã cho.
[A]. $ BM=1,5a. $
[B]. $ BM=a\sqrt{2}. $
[C]. $ BM=a\sqrt{3}. $
[D]. $ BM=\dfrac{a\sqrt{5}}{2}. $
Hướng dẫn giải:
$ M$ là trung điểm của $ AC\Rightarrow AM=\dfrac{AC}{2}=\dfrac{a}{2}. $
Tam giác $ \Delta BAM$ vuông tại $ A$ $ \Rightarrow BM=\sqrt{A{{B}^{2}}+A{{M}^{2}}}=\sqrt{{{a}^{2}}+\dfrac{{{a}^{2}}}{4}}=\dfrac{a\sqrt{5}}{2}. $
Chọn đáp án D.
Câu 11.
Tam giác $ ABC$ có $ AB=9$ cm, $ AC=12$ cm và $ BC=15$ cm. Tính độ dài đường trung tuyến $ AM$ của tam giác đã cho.
[A]. $ AM=\dfrac{15}{2}cm. $
[B]. $ AM=10cm. $
[C]. $ AM=9cm. $
[D]. $ AM=\dfrac{13}{2}cm. $
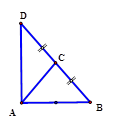
Hướng dẫn giải:
Áp dụng hệ thức đường trung tuyến $ m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}$ ta được: $ m_{a}^{2}=\dfrac{A{{C}^{2}}+A{{B}^{2}}}{2}-\dfrac{B{{C}^{2}}}{4}=\dfrac{{{12}^{2}}+{{9}^{2}}}{2}-\dfrac{{{15}^{2}}}{4}=\dfrac{225}{4}. $
$ \Rightarrow {{m}_{a}}=\dfrac{15}{2}. $ Chọn đáp án A.
Câu 12.
Tam giác $ ABC$ cân tại $ C$ , có $ AB=9\text{cm}$ và $ AC=\dfrac{15}{2}\text{cm}$ . Gọi $ D$ là điểm đối xứng của $ B$ qua $ C$ . Tính độ dài cạnh $ AD. $
[A]. $ AD=6$ $ cm. $
[B]. $ AD=9$ $ cm. $
[C]. $ AD=12$ $ cm. $
[D]. $ AD=12\sqrt{2}$ $ cm. $
Hướng dẫn giải:
Ta có: $ D$ là điểm đối xứng của $ B$ qua $ C$ $ \Rightarrow C$ là trung điểm của $ BD. $
$ \Rightarrow $ $ AC$ là trung tuyến của tam giác $ \Delta DAB. $
$ BD=2BC=2AC=15. $
Theo hệ thức trung tuyến ta có:
$ A{{C}^{2}}=\dfrac{A{{B}^{2}}+A{{D}^{2}}}{2}-\dfrac{B{{D}^{2}}}{4}$ $ \Rightarrow A{{D}^{2}}=2A{{C}^{2}}+\dfrac{B{{D}^{2}}}{2}-A{{B}^{2}}$
$ \Rightarrow A{{D}^{2}}=$ $ 2. {{\left( \dfrac{15}{2} \right)}^{2}}+\dfrac{{{15}^{2}}}{2}-{{9}^{2}}=144\Rightarrow AD=12. $ Chọn đáp án C.
Câu 13.
Tam giác $ ABC$ có $ AB=5,AC=9$ và đường trung tuyến $ AM=6. $ Tính độ dài cạnh $ BC. $
[A]. $ 2\sqrt{17}. $
[B]. $ \sqrt{17}. $
[C]. $ \sqrt{129}. $
[D]. $ 22. $
Hướng dẫn giải:
Áp dụng công thức đường trung tuyến trong tam giác ta có:
$ A{{M}^{2}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}}{2}-\dfrac{B{{C}^{2}}}{4}$
$ \Rightarrow BC=2\left( A{{B}^{2}}+A{{C}^{2}} \right)-4A{{M}^{2}}$ $ =2\left( {{5}^{2}}+{{9}^{2}} \right)-{{4. 6}^{2}}=68. $
$ \Rightarrow BC=\sqrt{68}=2\sqrt{17}. $
Chọn đáp án A.
Câu 14.
Tam giác $ ABC$ có $ AB=4,AC=10$ và đường trung tuyến $ AM=6. $ Tính độ dài cạnh $ BC. $
[A]. $ 2\sqrt{6}. $
[B]. $ 5. $
[C]. $ \sqrt{22}. $
[D]. $ 2\sqrt{22}. $
Hướng dẫn giải:
Áp dụng công thức đường trung tuyến trong tam giác ta có:
$ A{{M}^{2}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}}{2}-\dfrac{B{{C}^{2}}}{4}$
$ \Rightarrow BC=2\left( A{{B}^{2}}+A{{C}^{2}} \right)-4A{{M}^{2}}$ $ =2\left( {{4}^{2}}+{{10}^{2}} \right)-{{4. 6}^{2}}=88. $
$ \Rightarrow BC=\sqrt{88}=2\sqrt{22}. $
Chọn đáp án D.
Câu 15.
Tam giác $ ABC$ có $ AB=4,AC=6$ và đường trung tuyến $ BM=3. $ Tính độ dài cạnh $ BC. $
[A]. $ \sqrt{17}. $
[B]. $ 2\sqrt{5}. $
[C]. $ 4. $
[D]. $ 8. $
Hướng dẫn giải:
Áp dụng công thức đường trung tuyến trong tam giác ta có:
$ B{{M}^{2}}=\dfrac{B{{A}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}$
$ \Rightarrow 4B{{M}^{2}}=2B{{A}^{2}}+2B{{C}^{2}}-A{{C}^{2}}$
$ \Rightarrow B{{C}^{2}}=\dfrac{4B{{M}^{2}}-2B{{A}^{2}}+A{{C}^{2}}}{2}$ $ =\dfrac{{{4. 3}^{2}}-{{2. 4}^{2}}+{{6}^{2}}}{2}=20$
$ \Rightarrow BC=2\sqrt{5}. $
Chọn đáp án B.
Câu 16.
Hình bình hành có hai cạnh là $ 5$ và $ 9,$ một đường chéo bằng $ 11. $ Tìm đường chéo còn lại.
[A]. $ 9,5. $
[B]. $ 4\sqrt{6}. $
[C]. $ \sqrt{91}. $
[D]. $ 3\sqrt{10}. $
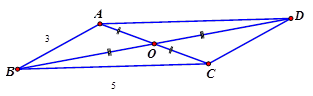
Hướng dẫn giải:
Hình bình hành $ ABCD$ có $ AB=5;BC=9. $
Gọi $ O=AC\cap BD\Rightarrow $ $ O$ là trung điểm của $ AC,BD. $
TH1: $ AC=11. $
$ \Rightarrow B{{O}^{2}}=\dfrac{B{{A}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}$ $ =\dfrac{{{5}^{2}}+{{9}^{2}}}{2}-\dfrac{{{11}^{2}}}{4}=\dfrac{91}{4}$
$ \Rightarrow BO=\dfrac{\sqrt{91}}{2}\Rightarrow BD=2BO=\sqrt{91}. $
TH2: $ BD=11\Rightarrow BO=\dfrac{11}{2}. $
Trong tam giác $ ABC$ ta có:
$ B{{O}^{2}}=\dfrac{B{{A}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}$
$ \Rightarrow A{{C}^{2}}=2\left( B{{A}^{2}}+B{{C}^{2}} \right)-4. B{{O}^{2}}$ $ =2\left( {{5}^{2}}+{{9}^{2}} \right)-4. {{\left( \dfrac{11}{2} \right)}^{2}}=91$
$ AC=\sqrt{91}$
Chọn đáp án C.
Câu 17.
Hình bình hành có hai cạnh là $ 3$ và $ 5$ một đường chéo bằng $ 5. $ Tìm đường chéo còn lại.
[A]. $ \sqrt{43}. $
[B]. $ 2\sqrt{13}. $
[C]. $ 8. $
[D]. $ 8\sqrt{3}. $
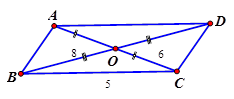
Hướng dẫn giải:
Hình bình hành $ ABCD$ có $ AB=3;BC=5. $
Gọi $ O=AC\cap BD\Rightarrow $ $ O$ là trung điểm của $ AC,BD. $
Đường chéo $ BD=5. $
Trong tam giác $ ABD$ ta có: $ A{{O}^{2}}=\dfrac{A{{B}^{2}}+A{{D}^{2}}}{2}-\dfrac{B{{D}^{2}}}{4}$ $ =\dfrac{{{3}^{2}}+{{5}^{2}}}{2}-\dfrac{{{5}^{2}}}{4}=\dfrac{43}{4}\Rightarrow AO=\dfrac{\sqrt{43}}{2}. $
$ \Rightarrow AC=2AO=\sqrt{43}. $
Chọn đáp án A.
Câu 18.
Hình bình hành có 1 cạnh là $ 5$ và hai đường chéo là $ 6$ và $ 8. $ Tính độ dài cạnh kề với cạnh có độ dài bằng $ 5. $
[A]. $ 3. $
[B]. $ 1. $
[C]. $ 5\sqrt{6}. $
[D]. $ 5. $
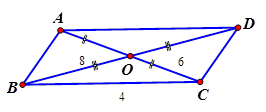
Hướng dẫn giải:
Hình bình hành $ ABCD$ có $ BC=5;AC=6;BD=8. $
Gọi $ O=AC\cap BD\Rightarrow O$ là trung điểm của $ BD$ và $ AC. $
Trong tam giác $ BCD$ ta có: $ CO$ là trung tuyến
$ \Rightarrow C{{O}^{2}}=\dfrac{C{{B}^{2}}+C{{D}^{2}}}{2}-\dfrac{B{{D}^{2}}}{4}$
$ \Rightarrow C{{D}^{2}}=\dfrac{4C{{O}^{2}}-2C{{B}^{2}}+B{{D}^{2}}}{2}$ $ =\dfrac{{{4. 3}^{2}}-{{2. 5}^{2}}+{{8}^{2}}}{2}=25$ $ \Rightarrow CD=5. $
Chọn đáp án D.
Câu 19.
Hình bình hành có 1 cạnh là $ 4$ và hai đường chéo là $ 6$ và $ 8. $ Tính độ dài cạnh kề với cạnh có độ dài bằng $ 4. $
[A]. $ \sqrt{34}. $
[B]. $ 6. $
[C]. $ \sqrt{42}. $
[D]. $ 5. $
Hướng dẫn giải:
Hình bình hành $ ABCD$ có $ BC=4;AC=6;BD=8. $
Gọi $ O=AC\cap BD\Rightarrow O$ là trung điểm của $ BD$ và $ AC. $
Trong tam giác $ BCD$ ta có: $ CO$ là trung tuyến
$ \Rightarrow C{{O}^{2}}=\dfrac{C{{B}^{2}}+C{{D}^{2}}}{2}-\dfrac{B{{D}^{2}}}{4}$
$ \Leftrightarrow 4C{{O}^{2}}=2\left( C{{B}^{2}}+C{{D}^{2}} \right)-B{{D}^{2}}$
$ \Rightarrow C{{D}^{2}}=\dfrac{4C{{O}^{2}}-2C{{B}^{2}}+B{{D}^{2}}}{2}$ $ =\dfrac{{{4. 3}^{2}}-{{2. 4}^{2}}+{{8}^{2}}}{2}=34$
$ \Rightarrow CD=\sqrt{34}. $
Chọn đáp án A.
Câu 20.
Tam giác $ ABC$ có $ AB=3,\,\,BC=8$ . Gọi $ M$ là trung điểm của $ BC$ . Biết $ \cos \widehat{AMB}=\dfrac{5\sqrt{13}}{26}$ và $ AM>3$ . Tính độ dài cạnh $ AC$ .
[A]. $ AC=\sqrt{13}. $
[B]. $ AC=\sqrt{7}. $
[C]. $ AC=13. $
[D]. $ AC=7. $
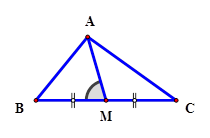
Hướng dẫn giải:
Ta có: $ M$ là trung điểm của $ BC$ $ \Rightarrow BM=\dfrac{BC}{2}=4. $
Trong tam giác $ ABM$ ta có: $ \cos \widehat{AMB}=\dfrac{A{{M}^{2}}+B{{M}^{2}}-A{{B}^{2}}}{2AM. BM}$
$ \Leftrightarrow A{{M}^{2}}-2AM. BM. \cos \widehat{AMB}+B{{M}^{2}}-A{{B}^{2}}=0. $
$ \Leftrightarrow A{{M}^{2}}-\dfrac{20\sqrt{13}}{13}AM+7=0\Leftrightarrow \left[ \begin{array}{l}
AM=\sqrt{13}>3\,\,\,(t/m) \\
AM=\dfrac{7\sqrt{13}}{13}<3\,\,\,(loai)
\end{array} \right. $
$ \Rightarrow AM=\sqrt{13}. $
Ta có: $ \widehat{AMB}$ và $ \widehat{AMC}$ là hai góc kề bù.
$ \Rightarrow \cos \widehat{AMC}=-\cos \widehat{AMB}=-\dfrac{5\sqrt{13}}{26}$
Trong tam giác $ \Delta AMC$ ta có:
$ A{{C}^{2}}=A{{M}^{2}}+C{{M}^{2}}-2AM. CM. \cos \widehat{AMC}$
$ =13+16-2. \sqrt{13}. 4. \left( -\dfrac{5\sqrt{13}}{26} \right)=49\Rightarrow AC=7. $ Chọn đáp án D.
Câu 21.
Tam giác $ ABC$ có trọng tâm $ G$ . Hai trung tuyến $ BM=6$ , $ CN=9$ và $ \widehat{BGC}={{120}^{0}}$ . Tính độ dài cạnh $ AB$ .
[A]. $ AB=\sqrt{11}$ .
[B]. $ AB=\sqrt{13}$ .
[C]. $ AB=2\sqrt{11}$ .
[D]. $ AB=2\sqrt{13}$ .
Hướng dẫn giải:
Ta có: $ \widehat{BGC}$ và $ \widehat{BGN}$ là hai góc kề bù mà $ \widehat{BGC}={{120}^{0}}\Rightarrow \widehat{BGN}={{120}^{0}}. $
$ G$ là trọng tâm của tam giác $ \Delta ABC$
$ \Rightarrow \left\{ \begin{array}{l}
BG=\dfrac{2}{3}BM=4. \\
GN=\dfrac{1}{3}CN=3.
\end{array} \right. $
Trong tam giác $ \Delta BGN$ ta có:
$ B{{N}^{2}}=G{{N}^{2}}+B{{G}^{2}}-2GN. BG. \cos \widehat{BGN}$
$ \Rightarrow B{{N}^{2}}=9+16-2. 3. 4. \dfrac{1}{2}=13\Rightarrow BN=\sqrt{13}. $
$ N$ là trung điểm của $ AB\Rightarrow AB=2BN=2\sqrt{13}. $ Chọn đáp án D.
Câu 22.
Cho tam giác $ ABC$ có $ AB=c,\text{ }BC=a,\text{ }CA=b$ . Nếu giữa $ a,\text{ }b,\text{ }c$ có liên hệ $ {{b}^{2}}+{{c}^{2}}=2{{a}^{2}}$ thì độ dài đường trung tuyến xuất phát từ đỉnh $ A$ của tam giác tính theo $ a$ bằng:
[A]. $ \dfrac{a\sqrt{3}}{2}. $
[B]. $ \dfrac{a\sqrt{3}}{3}. $
[C]. $ 2a\sqrt{3}. $
[D]. $ 3a\sqrt{3}. $
Hướng dẫn giải:
Hệ thức trung tuyến xuất phát từ đỉnh $ A$ của tam giác: $ m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}$
Mà: $ {{b}^{2}}+{{c}^{2}}=2{{a}^{2}}\Rightarrow $ $ m_{a}^{2}=\dfrac{2{{a}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}=\dfrac{3{{a}^{2}}}{4}\Rightarrow {{m}_{a}}=\dfrac{a\sqrt{3}}{2}. $ Chọn đáp án A.
Câu 23.
Tam giác $ ABC$ có tổng hai góc $ B$ và $ C$ bằng $ {{135}^{0}}$ và độ dài cạnh $ BC$ bằng $ a. $ Tính bán kính đường tròn ngoại tiếp tam giác.
[A]. $ \dfrac{a\sqrt{2}}{2}. $
[B]. $ a\sqrt{2}. $
[C]. $ \dfrac{a\sqrt{3}}{2}. $
[D]. $ a\sqrt{3}. $
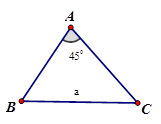
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow A={{180}^{0}}-\left( B+C \right)={{180}^{0}}-{{135}^{0}}={{45}^{0}}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{a}{\sin A}=2R\Rightarrow \dfrac{BC}{\sin A}=2R\Rightarrow R=\dfrac{BC}{2\sin A}=\dfrac{a}{2\sin {{45}^{0}}}=\dfrac{a}{2. \dfrac{\sqrt{2}}{2}}=\dfrac{a\sqrt{2}}{2}. $
Chọn đáp án A.
Câu 24.
Tính bán kính đường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=c$ và $ \cos \left( A+B \right)=\dfrac{1}{3}$
[A]. $ \dfrac{c\sqrt{2}}{2}. $
[B]. $ \dfrac{3c\sqrt{2}}{8}. $
[C]. $ \dfrac{9c\sqrt{2}}{8}. $
[D]. $ \dfrac{3c}{2}. $
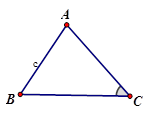
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \cos C=-\cos \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức: $ {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\Rightarrow {{\sin }^{2}}C=1-{{\cos }^{2}}C=1-\dfrac{1}{9}=\dfrac{8}{9}$
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{2\sqrt{2}}{3}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{c}{2. \dfrac{2\sqrt{2}}{3}}=\dfrac{3c\sqrt{2}}{8}. $
Chọn đáp án B.
Câu 25.
Tính bán kính đường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=10$ và $ \tan \left( A+B \right)=\dfrac{1}{3}$
[A]. $ \dfrac{5\sqrt{10}}{9}. $
[B]. $ \dfrac{10}{3}. $
[C]. $ \dfrac{\sqrt{10}}{5}. $
[D]. $ 5\sqrt{10}. $
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \tan C=-\tan \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức: \[\dfrac{1}{{{\cos }^{2}}\alpha }={{\tan }^{2}}\alpha +1\Rightarrow {{\cos }^{2}}\alpha =\dfrac{1}{{{\tan }^{2}}\alpha +1}\Rightarrow {{\cos }^{2}}C=\dfrac{1}{\dfrac{1}{9}+1}=\dfrac{9}{10}\]
$ \Rightarrow {{\sin }^{2}}C=1-{{\cos }^{2}}C=1-\dfrac{9}{10}=\dfrac{1}{10}$
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{\sqrt{10}}{10}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{10}{2. \dfrac{\sqrt{10}}{10}}=5\sqrt{10}. $
Chọn đáp án D.
Câu 26.
Tính bán kínhddường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=12$ và $ \cot \left( A+B \right)=\dfrac{1}{3}$
[A]. $ 2\sqrt{10}. $
[B]. $ \dfrac{9\sqrt{10}}{5}. $
[C]. $ 5\sqrt{10}. $
[D]. $ 3\sqrt{2}. $
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \cot C=-\cot \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức:
\[\dfrac{1}{{{\sin }^{2}}\alpha }={{\cot }^{2}}\alpha +1\Rightarrow {{\sin }^{2}}\alpha =\dfrac{1}{{{\cot }^{2}}\alpha +1}\Rightarrow {{\sin }^{2}}C=\dfrac{1}{\dfrac{1}{9}+1}=\dfrac{9}{10}\]
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{3\sqrt{10}}{10}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{12}{2. \dfrac{3\sqrt{10}}{10}}=2\sqrt{10}. $
Chọn đáp án A.
Câu 27.
Cho hình bình hành $ ABCD$ có $ AB=a,\text{ }BC=b,\text{ }BD=m$ và $ AC=n$ . Trong các biểu thức sau, biểu thức nào đúng:
[A]. $ {{m}^{2}}+{{n}^{2}}=3\left( {{a}^{2}}+{{b}^{2}} \right). $
[B]. $ {{m}^{2}}+{{n}^{2}}=2\left( {{a}^{2}}+{{b}^{2}} \right). $
[C]. \[2\left( {{m}^{2}}+{{n}^{2}} \right)={{a}^{2}}+{{b}^{2}}. \]
[D]. \[3\left( {{m}^{2}}+{{n}^{2}} \right)={{a}^{2}}+{{b}^{2}}. \]
Hướng dẫn giải:
Gọi $ O$ là giao điểm của $ AC$ và $ BD. $
Ta có: $ BO=\dfrac{1}{2}BD=\dfrac{m}{2}. $
$ BO$ là trung tuyến của tam giác $ \Delta ABC$
$ \Rightarrow B{{O}^{2}}=\dfrac{B{{A}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}$
$ \Leftrightarrow \dfrac{{{m}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{n}^{2}}}{4}\Leftrightarrow {{m}^{2}}+{{n}^{2}}=2\left( {{a}^{2}}+{{b}^{2}} \right)$ Chọn đáp án B.
Câu 28.
Tam giác $ ABC$ có $ AB=c,\text{ }BC=a,\text{ }CA=b$ . Các cạnh $ a,\text{ }b,\text{ }c$ liên hệ với nhau bởi đẳng thức $ {{a}^{2}}+{{b}^{2}}=5{{c}^{2}}$ . Góc giữa hai trung tuyến $ AM$ và $ BN$ là góc nào?
[A]. $ {{30}^{0}}. $
[B]. $ {{45}^{0}}. $
[C]. $ {{60}^{0}}. $
[D]. $ {{90}^{0}}. $
Hướng dẫn giải:
Gọi $ G$ là trọng tâm tam giác $ \Delta ABC. $
Ta có: $ A{{M}^{2}}=\dfrac{A{{C}^{2}}+A{{B}^{2}}}{2}-\dfrac{B{{C}^{2}}}{4}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}$
$ \Rightarrow A{{G}^{2}}=\dfrac{4}{9}A{{M}^{2}}=\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}$
$ B{{N}^{2}}=\dfrac{B{{A}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}=\dfrac{{{c}^{2}}+{{a}^{2}}}{2}-\dfrac{{{b}^{2}}}{4}$
$ \Rightarrow G{{N}^{2}}=\dfrac{1}{9}B{{N}^{2}}=\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}$
Trong tam giác $ \Delta AGN$ ta có:
\[\cos \widehat{AGN}=\dfrac{A{{G}^{2}}+G{{N}^{2}}-A{{N}^{2}}}{2. AG. GN}=\dfrac{\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}+\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}-\dfrac{{{b}^{2}}}{4}}{2. \sqrt{\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}}. \sqrt{\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}}}\]
\[=\dfrac{\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}+\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}-\dfrac{{{b}^{2}}}{4}}{2. \sqrt{\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}}. \sqrt{\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}}}\]
$ =\dfrac{10{{c}^{2}}-2\left( {{a}^{2}}+{{b}^{2}} \right)}{36. 2. \sqrt{\dfrac{2\left( {{b}^{2}}+{{c}^{2}} \right)}{9}-\dfrac{{{a}^{2}}}{9}}. \sqrt{\dfrac{{{c}^{2}}+{{a}^{2}}}{18}-\dfrac{{{b}^{2}}}{36}}}=0$ $ \Rightarrow \widehat{AGN}={{90}^{0}}. $
Câu 29.
Tam giác $ ABC$ có ba đường trung tuyến $ {{m}_{a}},\text{ }{{m}_{b}},\text{ }{{m}_{c}}$ thỏa mãn $ 5m_{a}^{2}=m_{b}^{2}+m_{c}^{2}$ . Khi đó tam giác này là tam giác gì?
[A]. Tam giác cân.
[B]. Tam giác đều.
[C]. Tam giác vuông.
[D]. Tam giác vuông cân.
Hướng dẫn giải:
Ta có: $ \left\{ \begin{array}{l}
m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4} \\
m_{b}^{2}=\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{{{b}^{2}}}{4} \\
m_{c}^{2}=\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}
\end{array} \right. $ Mà: $ 5m_{a}^{2}=m_{b}^{2}+m_{c}^{2}$
$ \Rightarrow 5\left( \dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4} \right)=\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{{{b}^{2}}}{4}+\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}$
$ \Leftrightarrow 10{{b}^{2}}+10{{c}^{2}}-5{{a}^{2}}=2{{a}^{2}}+2{{c}^{2}}-{{b}^{2}}+2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}}$
$ \Leftrightarrow {{b}^{2}}+{{c}^{2}}={{a}^{2}}\Rightarrow $ tam giác $ \Delta ABC$ vuông. Chọn đáp án C.
Câu 30.
Tam giác $ ABC$ có $ AB=c,\text{ }BC=a,\text{ }CA=b$ . Gọi $ {{m}_{a}},\text{ }{{m}_{b}},\text{ }{{m}_{c}}$ là độ dài ba đường trung tuyến, $ G$ trọng tâm. Xét các khẳng định sau:
$ \left( \text{I} \right)$ . $ m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=\dfrac{3}{4}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$ .
$ \left( \text{II} \right)$ . $ G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}=\dfrac{1}{3}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$ .
Trong các khẳng định đã cho có
[A]. $ \left( \text{I} \right)$ đúng.
[B]. Chỉ $ \left( \text{II} \right)$ đúng.
[C]. Cả hai cùng sai.
[D]. Cả hai cùng đúng.
Hướng dẫn giải
Ta có: $ \left\{ \begin{array}{l}
m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4} \\
m_{b}^{2}=\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{{{b}^{2}}}{4} \\
m_{c}^{2}=\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}
\end{array} \right. $ $ \Rightarrow m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=\dfrac{3}{4}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$
$ G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}=\dfrac{4}{9}\left( m_{a}^{2}+m_{b}^{2}+m_{c}^{2} \right)=\dfrac{4}{9}. \dfrac{3}{4}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)=\dfrac{1}{3}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$
Chọn đáp án D.
Câu 31.
Cho $ A=41{}^\circ ,\text{ }B=72{}^\circ $ và $ a=15$ . Tính c.
[A]. $ 19,6. $
[B]. $ 10,7. $
[C]. $ 21. $
[D].
D.
$ 7,8. $
Hướng dẫn giải:
$ C=180{}^\circ -\left( A+B \right)=180{}^\circ -\left( 41{}^\circ +72{}^\circ
\right)=67{}^\circ $
$ \dfrac{c}{\sin C}=\dfrac{a}{\sin A}\Rightarrow c=\dfrac{a\sin C}{\operatorname{sinA}}=\dfrac{15. \sin 67{}^\circ }{\sin 41{}^\circ }=21. 0$ . Chọn đáp án C.
Câu 32.
Cho $ B=24{}^\circ ,\text{ }C=87{}^\circ $ và $ a=113$ . Tính c.
[A]. $ 120,9. $
[B]. $ 49,2. $
[C]. $ 94,4. $
[D]. $ 142,7. $
Hướng dẫn giải:
$ A=180{}^\circ -\left( 24{}^\circ +87{}^\circ
\right)=69{}^\circ $
$ \dfrac{c}{\sin C}=\dfrac{113}{\sin 69{}^\circ }\Rightarrow c=\dfrac{113. \sin 87{}^\circ }{\sin 69{}^\circ }=120,9$ . Chọn đáp án A.
Câu 33.
Cho $ a=15,\text{ }b=19$ và $ A=82{}^\circ $ . Tính c.
[A]. $ 16,2$
và $ 1,4. $
[B]. $ 4,3. $
[C]. 7,6.
[D]. vô nghiệm.
Hướng dẫn giải:
$ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}\Rightarrow \sin B=\dfrac{b\sin A}{a}=\dfrac{19. \sin 82{}^\circ }{12}=1,568>1$ : vô lý
Vậy không có B, suy ra không có C. Chọn đáp án D.
Câu 34.
Cho $ b=41,6;\text{ }c=52,7$ và $ C=80,3{}^\circ $ . Tính $ B$ .
[A]. $ 77,7{}^\circ . $
[B]. $ 82,4{}^\circ . $
[C]. $ 51,1{}^\circ . $
[D]. $ 38,8{}^\circ . $
Hướng dẫn giải:
$ \sin B=\dfrac{b\sin C}{c}=\dfrac{41,6\sin 80,3{}^\circ }{52,7}\Rightarrow B=51,1{}^\circ $ . Chọn đáp án C.
Câu 35.
Cho $ a=91,60\text{ };\text{ }c=24,19$ và $ B=37{}^\circ $ . Tính diện tích tam giác $ S$ .
[A]. $ 1769,62. $
[B]. $ 666,75. $
[C]. $ 1107,91. $
[D]. $ 1212,54. $
Hướng dẫn giải:
$ S=\dfrac{1}{2}ac\sin B=\dfrac{1}{2}\times 91,60\times 24,19. \sin 37{}^\circ =666,75$ . Chọn đáp án B.
Câu 36.
Cho $ a=72,\text{ }b=51$ và $ A=27{}^\circ $ . Tính diện tích tam giác $ S$ .
[A]. \[833,5. \]
[B]. \[1315,2. \]
[C]. \[1635,9. \]
[D]. \[2630,6. \]
Hướng dẫn giải:
Cho $ a=72,b=51,\widehat{A}=27{}^\circ $ . Ta có :
$ \sin B=\dfrac{b\sin a}{a}=\dfrac{51. \sin 27{}^\circ }{72}=0,322\Rightarrow B=18,8{}^\circ $
$ C=180{}^\circ -\left( 27{}^\circ +18,8{}^\circ
\right)==134,2{}^\circ $
$ S=\dfrac{1}{2}ab\operatorname{sinC}=\dfrac{1}{2}\times 72\times 51\times \sin 134,2{}^\circ =1315,2$ . Chọn đáp án B.
Câu 37.
Cho tam giác $ ABC$ với ba cạnh có độ dài 4, 6, 8. Độ dài bán kính đường tròn nội tiếp tam giác $ ABC$ là:
[A]. $ \dfrac{\sqrt{15}}{2}. $
[B]. $ \dfrac{\sqrt{15}}{3}. $
[C]. $ \dfrac{\sqrt{15}}{4}. $
[D]. $ \dfrac{\sqrt{15}}{5}. $
Hướng dẫn giải:
Nửa chu vi của tam giác là $ p=\dfrac{a+b+c}{2}=\dfrac{4+6+8}{2}=9$
Diện tích tam giác là : $ S=pr=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}$
Do đó : $ 9. r=\sqrt{9\left( 9-4 \right)\left( 9-6 \right)\left( 9-8 \right)}\Rightarrow r=\dfrac{\sqrt{15}}{3}$ . Chọn đáp án B.
Câu 38.
Tam giác $ ABC$ có $ AB=6,\text{ }AC=10,\text{ }cosA=\dfrac{3}{5}$ . Diện tích tam giác là:
[A]. $ 12. $
[B]. $ 14. $
[C]. $ 20. $
[D]. $ 24. $
Hướng dẫn giải:
$ \cos A=\dfrac{3}{5}\Rightarrow {{\sin }^{2}}A=1-{{\left( \dfrac{3}{5} \right)}^{2}}=\dfrac{16}{25}\Rightarrow \sin A=\dfrac{4}{5}$
Diện tích $ S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}. 6. 10. \dfrac{4}{5}=24$ . Chọn đáp án D.
Câu 39.
Tam giác $ ABC$ có $ AB=8,\text{ }AC=5,\text{ }\widehat{BAC}=60{}^\circ $ . Chiều cao $ AH$ của tam giác là:
[A]. $ \dfrac{20\sqrt{3}}{7}. $
[B]. $ 40\sqrt{3}. $
[C]. $ 40\sqrt{7}. $
[D]. $ \dfrac{20\sqrt{21}}{7}. $
Hướng dẫn giải:
$ B{{C}^{2}}={{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A=82+52-2. 8. 5. cos60{}^\circ =49$ . Suy ra $ a=7$
$ S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}a{{h}_{a}}\Rightarrow AH={{h}_{a}}=\dfrac{bc. \sin A}{a}=\dfrac{8. 5. \dfrac{\sqrt{3}}{2}}{7}=\dfrac{20\sqrt{3}}{7}$ . Chọn đáp án A.
Câu 40.
Tam giác $ ABC$ có$ A=45{}^\circ ,a=2\sqrt{2},b=\sqrt{6}-\sqrt{2}$ . Tính cạnh $ c$ , ta được:
[A]. $ \sqrt{3}. $
[B]. $ 2\sqrt{3}. $
[C]. $ 4. $
[D]. $ 4\sqrt{2}. $
Hướng dẫn giải:
Từ $ {{a}^{2}}={{c}^{2}}+{{b}^{2}}-2cb\cos A$ ta có
$ {{\left( 2\sqrt{2} \right)}^{2}}={{\left( \sqrt{6}-\sqrt{2} \right)}^{2}}+{{c}^{2}}-2\left( \sqrt{6}-\sqrt{2} \right)c. \dfrac{\sqrt{2}}{2}$
Suy ra : $ 8=8-4\sqrt{3}+{{c}^{2}}-\sqrt{2}\left( \sqrt{6}-\sqrt{2} \right)c=0$
$ \Leftrightarrow {{c}^{2}}-2\left( \sqrt{3}-1 \right)c-4\sqrt{3}=0$ Có : $ \vartriangle ‘={{\left( \sqrt{3}-1 \right)}^{2}}+4\sqrt{3}={{\left( \sqrt{3}+1 \right)}^{2}}$
$ \Leftrightarrow \left[ \begin{array}{l}
c=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3} \\
c=\sqrt{3}-1-\sqrt{3}-1=-0<0)(L)
\end{array} \right. $
Vậy $ c=2\sqrt{3}$ . Chọn đáp án B.
Câu 41.
Cho tam giác $ ABC$ có $ AB=3,\text{ }AC=4$ , diện tích $ S=3\sqrt{3}$ . Giá trị của $ \cos A$ là:
[A]. $ \pm \dfrac{1}{3}. $
[B]. $ \dfrac{1}{2}. $
[C]. $ -\dfrac{1}{2}. $
[D]. $ \pm \dfrac{1}{2}. $
Hướng dẫn giải:
Từ $ S=\dfrac{1}{2}bc\sin A$ ta có : $ 3\sqrt{3}=\dfrac{1}{2}. 3. 4. \sin A\Leftrightarrow \sin A=\dfrac{\sqrt{3}}{2}$
$ {{\cos }^{2}}A=1-{{\sin }^{2}}A-1-\dfrac{3}{4}=\dfrac{1}{4}\Rightarrow \cos A=\pm \dfrac{1}{2}$ . Chọn đáp án D.
Câu 42.
Cho hình bình hành $ ABCD$ có diện tích $ S$ . Gọi $ M,N$ lần lượt là trung điểm của $ CD,\text{ }CB$ . Diện tích của tam giác $ AMN$ là:
[A]. $ \dfrac{1}{2}S. $
[B]. $ \dfrac{1}{3}S. $
[C]. $ \dfrac{3}{8}S. $
[D]. $ \dfrac{3}{7}S. $
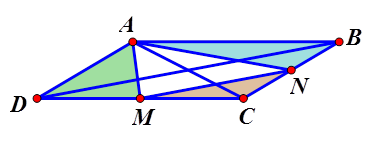
Hướng dẫn giải:
$ {{S}_{\Delta DAC}}={{S}_{\Delta BAC}}={{S}_{\Delta CBD}}=\dfrac{1}{2}{{S}_{ABCD}}$
$ \dfrac{{{S}_{\Delta DAM}}}{{{S}_{\Delta DAC}}}=\dfrac{\dfrac{1}{2}DA. DM. \sin \widehat{ADM}}{\dfrac{1}{2}DA. DC. \sin \widehat{ADC}}=\dfrac{DM}{DC}=\dfrac{1}{2}\Rightarrow {{S}_{\Delta DAM}}=\dfrac{1}{2}{{S}_{\Delta DAC}}=\dfrac{1}{4}{{S}_{ABCD}}=\dfrac{S}{4}. $
Tương tự ta có :
$ {{S}_{\Delta CMN}}=\dfrac{1}{4}{{S}_{\Delta CBD}}=\dfrac{1}{2}. \dfrac{1}{4}{{S}_{ABCD}}=\dfrac{S}{8}. $
$ {{S}_{\Delta BAN}}=\dfrac{1}{2}{{S}_{\Delta BAC}}=\dfrac{1}{2}. \dfrac{1}{2}{{S}_{ABCD}}=\dfrac{S}{4}$
$ {{S}_{\Delta AMN}}={{S}_{ABCD}}-{{S}_{\Delta DAM}}-{{S}_{\Delta CMN}}-{{S}_{\Delta ABN}}=S-\dfrac{S}{4}-\dfrac{S}{8}-\dfrac{S}{4}=\dfrac{3S}{8}. $
Chọn đáp án C.
Câu 43.
Cho tam giác $ ABC$ có 2 góc là $ 30{}^\circ ,\text{ }45{}^\circ $ , cạnh nhỏ nhất có độ dài bằng 10. Cạnh lớn nhất bằng số nào sau đây
[A]. \[15,2. \]
[B]. \[16,4. \]
[C]. \[19,4. \]
[D]. \[22,3. \]
Hướng dẫn giải:
Góc lớn nhất là $ 180{}^\circ -\left( 30{}^\circ +45{}^\circ
\right)=105{}^\circ $ . Gọi $ x$ là cạnh lớn nhất.
Ta có $ \dfrac{x}{\sin 105{}^\circ }=\dfrac{10}{\sin 30{}^\circ }\Rightarrow x=20\sin 105{}^\circ \approx 19,4$ . Chọn đáp án C.
Câu 44.
Cho tam giác $ ABC$ có 2 góc là $ 30{}^\circ ,\text{ }45{}^\circ $ , cạnh nhỏ nhất có độ dài bằng 10. Khi đó, bán kính đường tròn ngoại tiếp tam giác $ ABC$ là:
[A]. $ 10. $
[B]. $ 15. $
[C]. $ 20. $
[D]. $ 25. $
Hướng dẫn giải:
Cạnh nhỏ nhất là 10, góc nhỏ nhất là $ 30{}^\circ $ nên :
$ 2R=\dfrac{10}{\sin 30{}^\circ }=20\Rightarrow R=10$ . Chọn đáp án A.
Câu 45.
Cho hình thang $ ABCD$ vuông tại $ A,B$ có hai cạnh đáy $ AD=5a,\text{ }BC=3a,\text{ }AB=4a$ . Gọi $ I$ là trung điểm của $ AB$ . Diện tích tam giác $ ICD$ là:
[A]. $ 4{{a}^{2}}. $
[B]. $ 6{{a}^{2}}. $
[C]. $ 8{{a}^{2}}. $
[D]. $ 16{{a}^{2}}. $
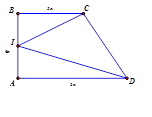
Hướng dẫn giải:
$ {{S}_{\Delta ICD}}={{S}_{ABCD}}-{{S}_{\Delta IBC}}-{{S}_{\Delta IAD}}$
$ =\dfrac{3a+5a}{2}. 4a-\left( \dfrac{1}{2}. 2a. 3a+\dfrac{1}{2}. 2a. 5a \right)=8{{a}^{2}}$
Chọn đáp án C.
Câu 46.
Tính diện tích tam giác có ba cạnh lần lượt là: $ 5,12,13. $
[A]. $ 60. $
[B]. $ 30. $
[C]. $ 34. $
[D]. $ 7\sqrt{5}. $
Hướng dẫn giải:
Ta có: $ {{5}^{2}}+{{12}^{2}}={{13}^{2}}$
$ \Rightarrow $ Độ dài 3 cạnh của tam giác vuông với 2 cạnh góc vuông lần lượt có độ dài là $ 5$ và $ 12. $
Diện tích tam giác: $ S=\dfrac{1}{2}. 5. 12=30. $
Chọn đáp án B.
Câu 47.
Tam giác có độ dài ba cạnh lần lượt là $ 5,12,13$ . Tính đường cao ứng với cạnh lớn nhất.
[A]. $ \dfrac{60}{13}. $
[B]. $ \dfrac{120}{13}. $
[C]. $ \dfrac{30}{13}. $
[D]. $ 12. $
Hướng dẫn giải:
Ta có: $ {{5}^{2}}+{{12}^{2}}={{13}^{2}}$
$ \Rightarrow $ Độ dài 3 cạnh của tam giác vuông với 2 cạnh góc vuông lần lượt có độ dài là $ 5$ và $ 12. $
Đường cao ứng với cạnh lớn nhất chính là đường cao ứng với cạnh huyền
Ta có: $ \dfrac{1}{{{h}^{2}}}=\dfrac{1}{{{5}^{2}}}+\dfrac{1}{{{12}^{2}}}=\dfrac{169}{3600}\Rightarrow h=\dfrac{60}{13}. $ Chọn đáp án A.
Câu 48.
Tam giác $ ABC$ có $ AB=12,AC=13,\widehat{A}={{30}^{0}}. $ Tính diện tích tam giác đó.
[A]. $ 39. $
[B]. $ 78. $
[C]. $ 39\sqrt{3}. $
[D]. $ 78\sqrt{3}. $
Hướng dẫn giải:
Diện tích tam giác: $ {{S}_{\Delta ABC}}=\dfrac{1}{2}AB. AC. \sin \widehat{A}=\dfrac{1}{2}. 12. 13. \sin {{30}^{0}}=39. $
Chọn đáp án A.
Câu 49.
Tam giác $ ABC$ có tổng hai góc $ B$ và $ C$ bằng $ {{135}^{0}}$ và độ dài cạnh $ BC$ bằng $ a. $ Tính bán kính đường tròn ngoại tiếp tam giác.
[A]. $ \dfrac{a\sqrt{2}}{2}. $
[B]. $ a\sqrt{2}. $
[C]. $ \dfrac{a\sqrt{3}}{2}. $
[D]. $ a\sqrt{3}. $
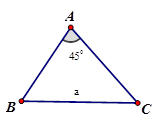
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow A={{180}^{0}}-\left( B+C \right)={{180}^{0}}-{{135}^{0}}={{45}^{0}}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{a}{\sin A}=2R\Rightarrow \dfrac{BC}{\sin A}=2R\Rightarrow R=\dfrac{BC}{2\sin A}=\dfrac{a}{2\sin {{45}^{0}}}=\dfrac{a}{2. \dfrac{\sqrt{2}}{2}}=\dfrac{a\sqrt{2}}{2}. $
Chọn đáp án A.
Câu 50.
Tính bán kính đường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=c$ và $ \cos \left( A+B \right)=\dfrac{1}{3}$
[A]. $ \dfrac{c\sqrt{2}}{2}. $
[B]. $ \dfrac{3c\sqrt{2}}{8}. $
[C]. $ \dfrac{9c\sqrt{2}}{8}. $
[D]. $ \dfrac{3c}{2}. $
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \cos C=-\cos \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức: $ {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\Rightarrow {{\sin }^{2}}C=1-{{\cos }^{2}}C=1-\dfrac{1}{9}=\dfrac{8}{9}$
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{2\sqrt{2}}{3}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{c}{2. \dfrac{2\sqrt{2}}{3}}=\dfrac{3c\sqrt{2}}{8}. $
Chọn đáp án B.
Câu 51.
Tính bán kính đường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=10$ và $ \tan \left( A+B \right)=\dfrac{1}{3}$
[A]. $ \dfrac{5\sqrt{10}}{9}. $
[B]. $ \dfrac{10}{3}. $
[C]. $ \dfrac{\sqrt{10}}{5}. $
[D]. $ 5\sqrt{10}. $
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \tan C=-\tan \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức:
\[\dfrac{1}{{{\cos }^{2}}\alpha }={{\tan }^{2}}\alpha +1\Rightarrow {{\cos }^{2}}\alpha =\dfrac{1}{{{\tan }^{2}}\alpha +1}\Rightarrow {{\cos }^{2}}C=\dfrac{1}{\dfrac{1}{9}+1}=\dfrac{9}{10}\]
$ \Rightarrow {{\sin }^{2}}C=1-{{\cos }^{2}}C=1-\dfrac{9}{10}=\dfrac{1}{10}$
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{\sqrt{10}}{10}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{10}{2. \dfrac{\sqrt{10}}{10}}=5\sqrt{10}. $ Chọn đáp án D.
Câu 52.
Tính bán kính dường tròn ngoại tiếp tam giác $ ABC$ biết $ AB=12$ và $ \cot \left( A+B \right)=\dfrac{1}{3}$
[A]. $ 2\sqrt{10}. $
[B]. $ \dfrac{9\sqrt{10}}{5}. $
[C]. $ 5\sqrt{10}. $
[D]. $ 3\sqrt{2}. $
Hướng dẫn giải:
Tổng ba góc trong tam giác bằng $ {{180}^{0}}\Rightarrow A+B+C={{180}^{0}}\Rightarrow C={{180}^{0}}-\left( A+B \right)$
$ \Rightarrow \cot C=-\cot \left( A+B \right)=-\dfrac{1}{3}. $
Áp dụng công thức:
\[\dfrac{1}{{{\sin }^{2}}\alpha }={{\cot }^{2}}\alpha +1\Rightarrow {{\sin }^{2}}\alpha =\dfrac{1}{{{\cot }^{2}}\alpha +1}\Rightarrow {{\sin }^{2}}C=\dfrac{1}{\dfrac{1}{9}+1}=\dfrac{9}{10}\]
$ 0<C<{{180}^{0}}\Rightarrow \sin C>0\Rightarrow \sin C=\dfrac{3\sqrt{10}}{10}. $
Áp dụng định lý sin trong tam giác ta có:
$ \dfrac{C}{\sin C}=2R\Rightarrow \dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2\sin C}=\dfrac{12}{2. \dfrac{3\sqrt{10}}{10}}=2\sqrt{10}. $ Chọn đáp án A.
Câu 53.
Tam giác $ ABC$ có độ dài ba trung tuyến lần lượt là $ 9;\text{ }12;\text{ }15$ . Diện tích của tam giác $ ABC$ bằng:
[A]. $ 24. $
[B]. $ 24\sqrt{2}. $
[C]. $ 72. $
[D]. $ 72\sqrt{2}. $
Hướng dẫn giải:
Ta có: $ \left\{ \begin{array}{l}
m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}=81 \\
m_{b}^{2}=\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{{{b}^{2}}}{4}=144 \\
m_{c}^{2}=\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}=225
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{{a}^{2}}=292 \\
{{b}^{2}}=208 \\
{{c}^{2}}=100
\end{array} \right. $ $ \Rightarrow \left\{ \begin{array}{l}
a=2\sqrt{73} \\
b=4\sqrt{13} \\
c=10
\end{array} \right. $
Ta có: $ \cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=\dfrac{208+100-292}{2. 4\sqrt{13}. 10}=\dfrac{1}{5\sqrt{13}}$
\[\sin A=\sqrt{1-{{\cos }^{2}}A}=\sqrt{1-{{\left( \dfrac{1}{5\sqrt{13}} \right)}^{2}}}=\dfrac{18\sqrt{13}}{65}. \]
Diện tích tam giác $ \Delta ABC: {{S}_{\Delta ABC}}=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}. 4\sqrt{13}. 10. \dfrac{18\sqrt{13}}{65}=72$
Câu 54.
Cho \[\Delta ABC\] có \[A\left( 1;-1 \right);B\left( 3;-3 \right);C\left( 6;0 \right)\]. Diện tích \[\Delta ABC\]là:
[A]. $ 12. $
[B]. $ 6. $
[C]. \[6\sqrt{2}. \]
[D]. $ 9. $
Hướng dẫn giải:
$ AB=\sqrt{4+4}=2\sqrt{2};AC=\sqrt{25+1}=\sqrt{26};BC=\sqrt{9+9}=3\sqrt{2}$
Ta có : $ A{{B}^{2}}+B{{C}^{2}}=8+18=26=A{{C}^{2}}\Rightarrow \Delta ABC$ vuông tại $ B. $
$ \Rightarrow {{S}_{\Delta ABC}}=\dfrac{1}{2}BA. BC=\dfrac{1}{2}. 2\sqrt{2}. 3\sqrt{2}=6. $ Chọn đáp án B.
Câu 55.
Giá trị nào sau đây là phương tích của điểm \[M\left( 1;2 \right)\]đối với đường tròn (C) tâm \[I\left( -2;1 \right)\], bán kính \[R=2\]:
[A]. $ 6. $
[B]. $ 8. $
[C]. $ 0. $
[D]. $ -5. $
Hướng dẫn giải:
Ta có: Phương tích của điểm $ M$ với đường tròn $ \left( C \right)$
$ {{\wp }_{M/\left( I \right)}}=I{{M}^{2}}-{{R}^{2}}=9+1-4=6. $ Chọn đáp án A.
Câu 56.
Cho đường tròn (C) đường kính AB với \[A\left( -1;-2 \right);B\left( 2;1 \right)\]. Kết quả nào sau đây là phương tích của điểm \[M\left( 1;2 \right)\] đối với đường tròn (C).
[A]. $ 3. $
[B]. $ 4. $
[C]. $ -5. $
[D]. $ 2. $
Hướng dẫn giải:
Đường tròn $ \left( C \right)$ có đường kính $ AB\Rightarrow $ tâm $ I$ là trung điểm của $ AB\Rightarrow I\left( \dfrac{1}{2};-\dfrac{1}{2} \right)$
Và bán kính $ R=\dfrac{AB}{2}=\dfrac{\sqrt{9+9}}{2}=\dfrac{3\sqrt{2}}{2}$
Phương tích của điểm $ M$ với đường tròn $ \left( C \right)$
$ {{\wp }_{M/\left( I \right)}}=I{{M}^{2}}-{{R}^{2}}=\dfrac{1}{4}+\dfrac{25}{4}-\dfrac{9}{2}=2. $ Chọn đáp án D.
Câu 57.
Khoảng cách từ A đến B không thể đo trực được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc \[{{78}^{0}}24’\] . Biết \[CA=250m,CB=120m\]. Khoảng cách AB bằng bao nhiêu?
[A]. $ 266m. $
[B]. $ 255m. $
[C]. $ 166m. $
[D]. $ 298m. $
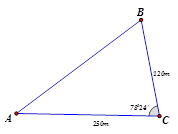
Hướng dẫn giải:
Dựa vào định lý cosin trong tam giác ta có:
$ A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}-2BC. AC. \cos \widehat{BAC}=64835,32473$
$ \Rightarrow AB\approx 255. $ Chọn đáp án B.
Câu 58.
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc
560 16 ‘ . Biết CA = 200m, CB = 180m. Khoảng cách AB bằng bao nhiêu?
[A]. $ 163m. $
[B]. $ 224m. $
[C]. $ 112m. $
[D]. $ 180m. $
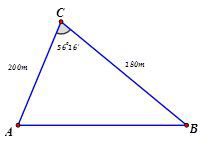
Hướng dẫn giải:
Dựa vào định lý cosin trong tam giác ta có:
$ A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}-2BC. AC. \cos \widehat{BAC}=32416,35917$
$ \Rightarrow AB\approx 180. $ Chọn đáp án D.
Câu 59.
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 600 . Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h . Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
[A]. $ 13. $
[B]. \[15\sqrt{13}. \]
[C]. \[20\sqrt{13}. \]
[D]. $ 15. $
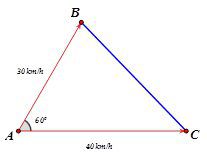
Hướng dẫn giải:
Sau $ 2$ giờ, quãng đường đi được của hai tầu lần lượt là: $ 60km$ và $ 80km. $
Gọi vị trí hai tàu khi đó là $ B,C$ như hình vẽ.
Khi đó, $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB. AC. \cos \widehat{BAC}={{60}^{2}}+{{80}^{2}}-2. 60. 80. \dfrac{1}{2}=5200$
$ \Rightarrow BC=20\sqrt{13}\Rightarrow $ Chọn đáp án C.
Câu 60.
Từ một đỉnh tháp chiều cao CD = 40m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc (so với phương thẳng đứng) là 720 12′ và 340 26′ . Ba điểm A, B, D thẳng hàng. Khoảng cách AB gần giá trị nào dưới đây nhất?
[A]. $ 71. $
[B]. $ 97. $
[C]. $ 79m. $
[D]. $ 40m. $
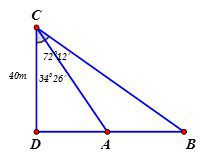
Hướng dẫn giải:
Trong tam giác vuông $ CDA$ ta có: $ AD=CD. \tan \widehat{DCA}=40. \tan {{34}^{0}}26’\approx 27,4. $
Trong tam giác vuông $ CDB$ ta có: $ DB=CD. \tan \widehat{DCB}=40. \tan {{72}^{0}}12’\approx 124,6$
$ \Rightarrow AB=BD-AD=124,6-27,4=97,2. $ Chọn đáp án B.