Tích vô hướng của hai véc tơ, trắc nghiệm toán 10
Câu 1.
Cho $ \overrightarrow{a}$ và $ \overrightarrow{b}$ thỏa $ \left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|=1$ và $ \left( \overrightarrow{a}+2\overrightarrow{b} \right)\bot \left( 5\overrightarrow{a}-4\overrightarrow{b} \right)$ . Tính $ \left( \overrightarrow{a},\overrightarrow{b} \right)$ .
[A]. $ {{30}^{0}}. $
[B]. $ {{60}^{0}}. $
[C]. $ {{120}^{0}}. $
[D]. $ {{150}^{0}}. $
Hướng dẫn giải:
$ \left( \overrightarrow{a}+2\overrightarrow{b} \right)\bot \left( 5\overrightarrow{a}-4\overrightarrow{b} \right)\Leftrightarrow \left( \overrightarrow{a}+2\overrightarrow{b} \right). \left( 5\overrightarrow{a}-4\overrightarrow{b} \right)=0$
$ \Leftrightarrow -3{{\overrightarrow{b}}^{2}}+6\overrightarrow{a}\overrightarrow{b}=0\Leftrightarrow \overrightarrow{a}. \overrightarrow{b}=\dfrac{1}{2}\Leftrightarrow \cos \left( \overrightarrow{a},\overrightarrow{b} \right)=\dfrac{1}{2}$ .
$ \Rightarrow \left( \vec{a},\vec{b} \right)={{60}^{0}}. $
Chọn đáp án B.
Câu 2.
. Cho
$ \left| \overrightarrow{a} \right|=2,\left| \overrightarrow{b} \right|=3,\left( \overrightarrow{a},\overrightarrow{b} \right)={{60}^{0}}$ . Tính giá trị biểu thức: $ A=\dfrac{1}{\overrightarrow{a}. \overrightarrow{b}-1}+\dfrac{1}{\overrightarrow{a}. \overrightarrow{b}-2}$
[A]. $ \dfrac{3}{2}. $
[B]. $ 1. $
[C]. $ \dfrac{1}{2}. $
[D]. $ 2. $
Hướng dẫn giải:
$ \overrightarrow{a}. \overrightarrow{b}=\left| \overrightarrow{a} \right|. \left| \overrightarrow{b} \right|. \cos \left( \overrightarrow{a},\overrightarrow{b} \right)=3$ . Vậy $ A=\dfrac{1}{2}+1=\dfrac{3}{2}$ .
Chọn đáp án A.
Câu 3.
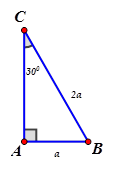
Cho $ \Delta ABC$ vuông tại A, đường cao AH có \[AB=a,\text{ }BC=2AB,\] giá trị $ \overrightarrow{CA}. \overrightarrow{CB}+\overrightarrow{BA}. \overrightarrow{BC}$ là :
[A]. $ 2{{a}^{2}}. $
[B]. $ 4{{a}^{2}}. $
[C]. $ {{a}^{2}}. $
[D]. $ 3{{a}^{2}}. $
Hướng dẫn giải:
Ta có: $ AB=\dfrac{1}{2}BC\Rightarrow \widehat{ACB}={{30}^{0}}. $
(Trong tam giác vuông, cạnh đối diện góc $ {{30}^{0}}$ thì có độ dài bằng $ \dfrac{1}{2}$ cạnh huyền)
$ \Rightarrow AC=\dfrac{AB}{\tan {{30}^{0}}}=a\sqrt{3}. $
$ \overrightarrow{CA}. \overrightarrow{CB}=CA. CB$
$ \overrightarrow{CA}. \overrightarrow{CB}+\overrightarrow{BA}. \overrightarrow{BC}=C{{A}^{2}}+B{{A}^{2}}={{\left( a\sqrt{3} \right)}^{2}}+{{a}^{2}}=4{{a}^{2}}. $
Chọn đáp án B.
Câu 4.
Cho $ \left| \overrightarrow{a} \right|+\left| \overrightarrow{b} \right|=2$ và $ \left( \overrightarrow{a};\overrightarrow{b} \right)={{0}^{0}},\left| 2\overrightarrow{a}+\overrightarrow{b} \right|=3$ . Tìm $ \left| \overrightarrow{a} \right|$ và $ \left| \overrightarrow{b} \right|$ .
[A]. $ \left| \overrightarrow{a} \right|=\dfrac{5}{3};\left| \overrightarrow{b} \right|=\dfrac{1}{3}. $
[B]. $ \left| \overrightarrow{a} \right|=\dfrac{4}{5};\left| \overrightarrow{b} \right|=\dfrac{6}{5}. $
[C]. $ \left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|=1. $
[D]. $ \left| \overrightarrow{a} \right|=\dfrac{1}{2};\left| \overrightarrow{b} \right|=\dfrac{3}{2}. $
Hướng dẫn giải:
$ \left| 2\overrightarrow{a}+\overrightarrow{b} \right|=3\Leftrightarrow 4{{\overrightarrow{a}}^{2}}+{{\overrightarrow{b}}^{2}}+4\overrightarrow{a}. \overrightarrow{b}=9$
$ \Leftrightarrow 4{{\left| {\vec{a}} \right|}^{2}}+4\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \left( \vec{a};\vec{b} \right)+{{\left| {\vec{b}} \right|}^{2}}=9$
$ \Leftrightarrow 4{{\left( 2-\left| {\vec{b}} \right| \right)}^{2}}+4\left( 2-\left| {\vec{b}} \right| \right)\left| {\vec{b}} \right|+{{\left| {\vec{b}} \right|}^{2}}=9$
$ \Leftrightarrow {{\left| {\vec{b}} \right|}^{2}}-8\left| {\vec{b}} \right|+7=0\Leftrightarrow \left[ \begin{array}{l}
\left| {\vec{b}} \right|=1\Rightarrow \left| {\vec{a}} \right|=1 \\
\left| {\vec{b}} \right|=7\Rightarrow \left| {\vec{a}} \right|=-5\,\,(loai)
\end{array} \right. $
Vậy, $ \left| {\vec{a}} \right|=1,\left| {\vec{b}} \right|=1. $
Chọn đáp án C.
.
Câu 5.
Cho $ \left| \overrightarrow{a} \right|=4,\left| \overrightarrow{b} \right|=6$
và $ \left| \overrightarrow{a}-\overrightarrow{b} \right|=2\sqrt{29}$ . Tính $ \left( \overrightarrow{a},\overrightarrow{b} \right)$ .
[A]. $ {{30}^{0}}. $
[B]. $ {{60}^{0}}. $
[C]. $ {{120}^{0}}. $
[D]. $ {{150}^{0}}. $
Hướng dẫn giải:
$ \left| \overrightarrow{a}-\overrightarrow{b} \right|=2\sqrt{19}\Leftrightarrow {{\overrightarrow{a}}^{2}}-2\overrightarrow{a}. \overrightarrow{b}+{{\overrightarrow{b}}^{2}}=76$ $ \Rightarrow \cos \left( \overrightarrow{a},\overrightarrow{b} \right)=-\dfrac{1}{2}\Rightarrow \left( \overrightarrow{a},\overrightarrow{b} \right)={{120}^{0}}$ .
Chọn đáp án C.
Câu 6.
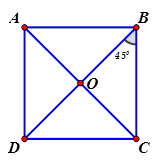
Cho hình vuông \[ABCD\] tâm $ O$ , cạnh $ a$ . Tính $ \overrightarrow{BO}. \overrightarrow{BC}$ ta được :
[A]. \[{{a}^{2}}. \]
[B]. \[-{{a}^{2}}. \]
[C]. \[\dfrac{3}{2}{{a}^{2}}. \]
[D]. \[\dfrac{{{a}^{2}}}{2}. \]
Hướng dẫn giải:
$ BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}. $
\[\overrightarrow{BO}. \overrightarrow{BC}=BO. BC. \cos \left( \overrightarrow{BO},\overrightarrow{BC} \right)=\dfrac{a\sqrt{2}}{2}. a. \dfrac{\sqrt{2}}{2}=\dfrac{{{a}^{2}}}{2}. \]
Chọn đáp án D.
.
Câu 7.
Cho
$ \left| \overrightarrow{a} \right|=2$ và
$ \left( \overrightarrow{a},\overrightarrow{b} \right)={{30}^{0}},\left| \overrightarrow{a}-2\overrightarrow{b} \right|=2,\overrightarrow{b}\ne \overrightarrow{0}$ . Tính $ \left| \overrightarrow{b} \right|$ .
[A]. $ \sqrt{2}. $
[B]. $ \sqrt{3}. $
[C]. $ 1. $
[D]. $ 2. $
Hướng dẫn giải:
$ \left| \overrightarrow{a}-2\overrightarrow{b} \right|=2\Leftrightarrow {{\overrightarrow{a}}^{2}}+4{{\overrightarrow{b}}^{2}}-4\left| \overrightarrow{a} \right|. \left| \overrightarrow{b} \right|. \cos \left( \overrightarrow{a},\overrightarrow{b} \right)={{2}^{2}}$ .
$ \Leftrightarrow 4+4{{\left| \overrightarrow{b} \right|}^{2}}-8. \left| \overrightarrow{b} \right|. \dfrac{\sqrt{3}}{2}={{2}^{2}}\Leftrightarrow 4{{\left| \overrightarrow{b} \right|}^{2}}-4\sqrt{3}\left| \overrightarrow{b} \right|+4-{{2}^{2}}=0$
$ \Leftrightarrow 4{{\left| \overrightarrow{b} \right|}^{2}}-4\sqrt{3}\left| \overrightarrow{b} \right|=0\Rightarrow \left| \overrightarrow{b} \right|=\sqrt{3}. $
Chọn đáp án B.
Câu 8.
Cho tam giác \[ABC\] có \[AB=2cm,BC=3cm,CA=5cm\]. Tính \[\overrightarrow{CA}. \overrightarrow{CB}\] là:
[A]. $ 13. $
[B]. $ 15. $
[C]. $ 17. $
[D]. Kết quả khác.
Hướng dẫn giải:
$ {{2}^{2}}=A{{B}^{2}}={{\overrightarrow{AB}}^{2}}={{\left( \overrightarrow{CB}-\overrightarrow{CA} \right)}^{2}}=C{{B}^{2}}-2\overrightarrow{CB}. \overrightarrow{CA}+C{{A}^{2}}$
$ \Rightarrow \overrightarrow{CA}. \overrightarrow{CB}=\dfrac{C{{B}^{2}}+C{{A}^{2}}-A{{B}^{2}}}{2}=\dfrac{{{3}^{2}}+{{5}^{2}}-{{2}^{2}}}{2}=15. $
Chọn đáp án B.
Câu 9.
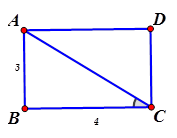
Cho hình chữ nhật ABCD có \[AB=3,BC=4\]. Giá trị \[\overrightarrow{AC}. \overrightarrow{CB}\] bằng
[A]. $ -16. $
[B]. $ 16. $
[C]. $ -20. $
[D]. $ 20. $
Hướng dẫn giải:
Ta có: \[\cos \left( \overrightarrow{CA},\overrightarrow{CB} \right)=\cos \widehat{ACB}=\dfrac{BC}{AC}=\dfrac{4}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=\dfrac{4}{5}\]
\[\overrightarrow{AC}. \overrightarrow{CB}=-\overrightarrow{CA}. \overrightarrow{CB}-CA. CB. \cos \left( \overrightarrow{CA},\overrightarrow{CB} \right)=-5. 4. \dfrac{4}{5}=-16. \]
Chọn đáp án A.
Câu 10.
Gọi $ G$ là trọng tâm tam giác đều $ ABC$ có cạnh bằng $ a$ . Trong các mệnh đề sau, tìm mệnh đề sai ?
[A]. $ \overrightarrow{AB}. \overrightarrow{AC}=\dfrac{1}{2}{{a}^{2}}$
[B]. $ \overrightarrow{AC}. \overrightarrow{CB}=-\dfrac{1}{2}{{a}^{2}}$
[C]. $ \overrightarrow{GA}. \overrightarrow{GB}=\dfrac{{{a}^{2}}}{6}$
[D]. $ \overrightarrow{AB}. \overrightarrow{AG}=\dfrac{1}{2}{{a}^{2}}$
Hướng dẫn giải:
Ta có: $ \left( \overrightarrow{GA},\overrightarrow{GB} \right)={{120}^{0}}\Rightarrow \cos \left( \overrightarrow{GA},\overrightarrow{GB} \right)<0\Rightarrow \overrightarrow{GA}. \overrightarrow{GB}<0$
Chọn đáp án C.