Bài toán trục tọa độ, hệ trục tọa độ, trắc nghiệm toán 10
Câu 1.
Cho ba điểm $ A,\,\,B,\,\,C$ trên trục $ x’Ox$ có vectơ đơn vị $ \overrightarrow{i}$ . Mệnh đề nào sau đây sai?
[A]. $ {{x}_{A}}$ là tọa độ của $ A\Leftrightarrow \overrightarrow{OA}={{x}_{A}}. \overrightarrow{i}$ .
[B]. $ {{x}_{B}},\,\,{{x}_{C}}$ là tọa độ của $ B$ và $ C$ thì : $ \overline{BC}={{x}_{B}}-{{x}_{C}}$ .
[C]. $ \overline{AC}+\overline{CB}=\overline{AB}$ .
[D]. $ M$ là trung điểm của $ AB\Leftrightarrow \overline{OM}=\dfrac{\overline{OA}+\overline{OB}}{2}$ .
Hướng dẫn giải:
Ta có: $ \overline{BC}={{x}_{C}}-{{x}_{B}}$ . Chọn đáp án B.
Câu 2.
Trên trục $ x’Ox$ , cho bốn điểm $ A,\,\,B,\,\,C,\,\,D$ có tọa độ lần lượt là $ 3,\,\,5,\,\,-7,\,\,9$ . Mệnh đề nào sau đây sai ?
[A]. $ \overline{AB}=2$ .
[B]. $ \overline{AC}=-10$ .
[C]. $ \overline{CD}=-16$ .
[D]. $ \overline{AB}+\overline{AC}=-8$ .
Hướng dẫn giải:
$ \overline{AB}=2,\,\,\overline{AC}=-10,\,\,\overline{CD}={{x}_{D}}-{{x}_{C}}=9-\left( -7 \right)=16,\,\,\overline{AB}+\overline{AC}=-8$ . Chọn đáp án C.
Câu 3.
Cho bốn điểm $ A,\,\,B,\,\,C,\,\,D$ trên trục $ \left( O\,;\,\overrightarrow{i} \right)$ . Mệnh đề nào sau đây sai ?
[A]. $ \overline{AB}=\overline{AD}+\overline{DB}$ .
[B]. $ \overline{AB}+\overline{CD}+\overline{BC}=\overline{AD}$ .
[C]. $ \overline{CD}=\overline{BD}-\overline{BC}$ .
[D]. $ \overline{AB}-\overline{BA}=0$ .
Hướng dẫn giải:
$ \overline{AB}-\overline{BA}=\overline{AB}+\overline{AB}=2\overline{AB}$ . Chọn đáp án D.
Câu 4.
Trên trục $ x’Ox$ cho hai điểm $ A,\,\,B$ có tọa độ lần lượt là 5 và 10. Điểm $ M$ nằm trên $ x’Ox$ thỏa $ 5\overrightarrow{MA}=3\overrightarrow{MB}$ có tọa độ là :
[A]. $ \dfrac{5}{2}$ .
[B]. $ -\dfrac{5}{2}$ .
[C]. $ \dfrac{3}{2}$ .
[D]. $ -2$ .
Hướng dẫn giải:
$ 5\overrightarrow{MA}=3\overrightarrow{MB}\Leftrightarrow 5\overline{MA}=3\overline{MB}\Leftrightarrow 5\left( 5-x \right)=3\left( 10-x \right)\Leftrightarrow x=-\dfrac{5}{2}$ . Chọn đáp án B.
Câu 5.
Trên trục $ x’Ox$ , cho ba điểm $ A,\,\,B,\,\,C$ . Nếu biết $ \overline{AB}=5,\,\,\overline{AC}=7$ thì $ \overline{CB}$ bằng :
[A]. $ -2$ .
[B]. $ 2$ .
[C]. $ 4$ .
[D]. $ 3$ .
Hướng dẫn giải:
$ \overline{CB}=\overline{AB}-\overline{AC}=5-7=-2$ . Chọn đáp án A.
Câu 6.
Trên trục $ \left( O\,;\,\overrightarrow{i} \right)$ , cho bốn điểm $ A,\,\,B,\,\,C,\,\,D$ có tọa độ lần lượt là $ a,\,\,b,\,\,c,\,\,d$ và điểm $ M$ có tọa độ $ x$ . Hỏi mệnh đề nào sau đây sai ?
[A]. Nếu $ \overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$ thì $ x=\dfrac{a+b}{2}$ .
[B]. Nếu $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}$ thì $ x=\dfrac{a+b+c}{3}$ .
[C]. Nếu $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{0}$ thì $ x=\dfrac{a+b+c+d}{4}$ .
[D]. $ \overline{MA}+\overline{AB}+\overline{BD}+\overline{MD}=0$ .
Hướng dẫn giải:
$ \overline{MA}+\overline{AB}+\overline{BD}+\overline{MD}=\overline{MB}+\overline{BD}+\overline{MD}=\overline{MD}+\overline{MD}=2\overline{MD}$ . Chọn đáp án D.
Câu 7.
Cho ba điểm $ A,\,\,B,\,\,C$ có tọa độ theo thứ tự là $ 2,\,\,4,\,\,-5$ . Tìm tọa độ điểm $ M$ trên trục này sao cho $ 3\overrightarrow{MA}+4\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$ .
[A]. $ \dfrac{4}{3}$ .
[B]. $ -\dfrac{2}{3}$ .
[C]. $ \dfrac{7}{9}$ .
[D]. Một số khác.
Hướng dẫn giải:
$ 3\overrightarrow{MA}+4\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow 3\overline{MA}+4\overline{MB}+2\overline{MC}=0$ $ \Leftrightarrow 3\left( 2-x \right)+4\left( 4-x \right)+2\left( -5-x \right)=0$
$ \Leftrightarrow 9x=12\Leftrightarrow x=\dfrac{4}{3}$ . Chọn đáp án A.
Câu 8.
Cho bốn điểm $ A,\,\,B,\,\,C,\,\,D$ trên một trục $ \left( O\,;\,\overrightarrow{i} \right)$ , có tọa độ lần lượt là $ a,\,\,b,\,\,c,\,\,d$ . Tìm hệ thức giữa $ a,\,\,b,\,\,c,\,\,d$ để $ \dfrac{\overline{CA}}{\overline{CB}}=-\dfrac{\overline{DA}}{\overline{DB}}$ .
[A]. $ \left( a+b \right)\left( c+d \right)=ab+cd$ .
[B]. $ \left( a+b \right)\left( c+d \right)=2\left( ab+cd \right)$ .
[C]. $ \left( a+b \right)\left( c+d \right)=ab-cd$ .
[D]. $ \left( a+b \right)\left( c+d \right)=2\left( ab-cd \right)$ .
Hướng dẫn giải:
$ \dfrac{\overline{CA}}{\overline{CB}}=-\dfrac{\overline{DA}}{\overline{DB}}\Leftrightarrow \overline{CA}. \overline{DB}+\overline{CB}. \overline{DA}=0$
$ \Leftrightarrow \left( a-c \right)\left( b-d \right)+\left( b-c \right)\left( a-d \right)=0\Leftrightarrow ab-ad-bc+cd+ab-bd-ac+cd=0$
$ \Leftrightarrow 2\left( ab+cd \right)=a\left( c+d \right)+b\left( c+d \right)=\left( a+b \right)\left( c+d \right)$ . Chọn đáp án B.
Câu 9.
Cho hai điểm $ A,\,\,B$ trên trục $ x’Ox$ có tọa độ 2 và 5. Tìm điểm $ C$ đối xứng với $ B$ qua điểm $ A$ .
[A]. $ -1$ .
[B]. $ -2$ .
[C]. $ 1$ .
[D]. $ 2$ .
Hướng dẫn giải:
$ C$ đối xứng với $ B$ qua $ A$ $ \Leftrightarrow A$ là trung điểm của $ BC$
$ \Leftrightarrow 2=\dfrac{5+{{x}_{C}}}{2}\Leftrightarrow {{x}_{C}}=-1$ . Chọn đáp án A.
Câu 10.
Trong hệ trục $ \left( O\,\,;\,\overrightarrow{i},\overrightarrow{j} \right)$ cho 2 vectơ $ \overrightarrow{a}=\left( 3\,\,;\,\,2 \right)$ , $ \overrightarrow{b}=-\overrightarrow{i}+5\overrightarrow{j}$ . Mệnh đề nào sau đây sai ?
[A]. $ \overrightarrow{a}=3\,\overrightarrow{i}+2\,\overrightarrow{j}$ .
[B]. $ \overrightarrow{b}=\left( -1\,;\,\,5 \right)$ .
[C]. $ \overrightarrow{a}+\overrightarrow{b}=\left( 2\,\,;\,\,7 \right)$ .
[D]. $ \overrightarrow{a}-\overrightarrow{b}=\left( 2\,\,;\,\,-3 \right)$ .
Hướng dẫn giải:
$ \overrightarrow{a}=\left( 3\,\,;\,\,2 \right),\,\,\overrightarrow{b}=\left( -1\,\,;\,\,5 \right)\Rightarrow \overrightarrow{a}-\overrightarrow{b}=\left( 4\,\,;-3 \right)$ . Chọn đáp án D.
Câu 11.
Cho $ \overrightarrow{a}=2\overrightarrow{i}-3\overrightarrow{j}$ và $ \overrightarrow{b}=-\overrightarrow{i}+2\overrightarrow{j}$ . Tìm tọa độ của $ \overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}$ .
[A]. $ \overrightarrow{c}=\left( 1\,\,;\,-1 \right)$ .
[B]. $ \overrightarrow{c}=\left( 3\,\,;\,-5 \right)$ .
[C]. $ \overrightarrow{c}=\left( -3\,\,;\,\,5 \right)$ .
[D]. $ \overrightarrow{c}=\left( 2\,\,;\,\,7 \right)$ .
Hướng dẫn giải:
$ \overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}=\left( 2\overrightarrow{i}-3\overrightarrow{j} \right)-\left( -\overrightarrow{i}+2\overrightarrow{j} \right)=3\overrightarrow{i}-5\overrightarrow{j}\Rightarrow \overrightarrow{c}=\left( 3\,\,;-5 \right)$ . Chọn đáp án B.
Câu 12.
Cho $ \overrightarrow{u}=2\overrightarrow{i}-3\overrightarrow{j}$ , $ \overrightarrow{v}=-5\,\overrightarrow{i}-\overrightarrow{j}$ . Gọi $ \left( X;Y \right)$ là tọa độ của $ \overrightarrow{w}=2\overrightarrow{u}-3\overrightarrow{v}$ thì tích $ XY$ bằng :
[A]. $ -57$ .
[B]. $ 57$ .
[C]. $ -63$ .
[D]. Một đáp án khác.
Hướng dẫn giải:
$ \overrightarrow{w}=2\overrightarrow{u}-3\overrightarrow{v}=2\left( 2\overrightarrow{i}-3\overrightarrow{j} \right)-3\left( -5\overrightarrow{i}-\overrightarrow{j} \right)=19\overrightarrow{i}-3\overrightarrow{j}$ .
$ X=19,\,\,Y=-3\Rightarrow XY=-57$ . Chọn đáp án A.
Câu 13.
Trọng tâm $ G$ của tam giác $ ABC$ với $ A\left( -4\,\,;\,\,7 \right),B\left( 2\,\,;\,\,5 \right),C\left( -1\,\,;-3 \right)$ có tọa độ là :
[A]. $ \left( -1\,\,;\,\,4 \right)$ .
[B]. $ \left( 2\,\,;\,\,6 \right)$ .
[C]. $ \left( -1\,\,;\,\,2 \right)$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ \left\{ \begin{array}{l}
{{x}_{G}}=\dfrac{-4+2-1}{3}=-1 \\
{{y}_{G}}=\dfrac{7+5-3}{3}=3
\end{array} \right. \Rightarrow G\left( -1\,\,;\,\,3 \right)$ . Chọn đáp án D.
Câu 14.
Cho $ A\left( 1\,\,;\,\,5 \right),B\left( -2\,\,;\,\,4 \right),G\left( 3\,\,;\,\,3 \right)$ . Nếu $ G$ là trọng tâm tam giác $ ABC$ thì tọa độ của $ C$ là:
[A]. $ \left( 3\,\,;\,\,1 \right)$ .
[B]. $ \left( 5\,\,;\,\,7 \right)$ .
[C]. $ \left( 10\,\,;\,\,0 \right)$ .
[D]. $ \left( -10\,\,;\,\,0 \right)$ .
Hướng dẫn giải:
$ \left\{ \begin{array}{l}
{{x}_{A}}+{{x}_{B}}+{{x}_{C}}=3{{x}_{G}} \\
{{y}_{A}}+{{y}_{B}}+{{y}_{C}}=3{{y}_{G}}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
1-2+{{x}_{C}}=9 \\
5+4+{{y}_{C}}=9
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{{x}_{C}}=10 \\
{{y}_{C}}=0
\end{array} \right. $ . Chọn đáp án C.
Câu 15.
Tìm tọa độ trung điểm $ M$ của đoạn nối hai điểm $ A\left( 3\,\,;\,\,7 \right)$ và $ B\left( -6\,\,;\,\,1 \right)$ .
[A]. $ \left( \dfrac{9}{2}\,\,;\,\,3 \right)$ .
[B]. $ \left( -\dfrac{3}{2}\,\,;\,\,4 \right)$ .
[C]. $ \left( -3\,\,;\,\,6 \right)$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ \left\{ \begin{array}{l}
{{x}_{M}}=\dfrac{{{x}_{A}}+{{x}_{B}}}{2}=\dfrac{3-6}{2}=-\dfrac{3}{2} \\
{{y}_{M}}=\dfrac{{{y}_{A}}+{{y}_{B}}}{2}=\dfrac{7+1}{2}=4
\end{array} \right. \Rightarrow M\left( -\dfrac{3}{2}\,\,;\,\,4 \right)$ . Chọn đáp án B.
Câu 16.
Cho $ A\left( 0\,\,;-2 \right)$ , $ B\left( -3\,\,;\,\,1 \right)$ . Tìm tọa độ giao điểm $ M$ của $ AB$ với trục $ x’Ox$ .
[A]. $ M\left( -2\,\,;\,\,0 \right)$ .
[B]. $ M\left( 2\,\,;\,\,0 \right)$ .
[C]. $ M\left( -\dfrac{1}{2}\,\,;\,\,0 \right)$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ M\left( x\,\,;\,\,0 \right)\in x’Ox\Rightarrow \overrightarrow{AM}=\left( x\,\,;\,\,2 \right)\,\,;\,\,\overrightarrow{AB}=\left( -3\,\,;\,\,3 \right). $
$ A,\,\,B,\,\,M$ thẳng hàng $ \Leftrightarrow \overrightarrow{AB},\overrightarrow{AM}$ cùng phương$ \Leftrightarrow \dfrac{x}{-3}=\dfrac{2}{3}\Leftrightarrow x=-2$ .
Vậy, $ M\left( -2\,\,;\,\,0 \right)$ . Chọn đáp án A.
Câu 17.
Cho $ \overrightarrow{a}=2\overrightarrow{i}-3\overrightarrow{j}$ , $ \overrightarrow{b}=m\,\overrightarrow{j}+\overrightarrow{i}$ . Nếu $ \overrightarrow{a},\,\,\overrightarrow{b}$ cùng phương thì :
[A]. $ m=-6$ .
[B]. $ m=6$ .
[C]. $ m=-\dfrac{2}{3}$ .
[D]. $ m=-\dfrac{3}{2}$ .
Hướng dẫn giải:
$ \overrightarrow{a}=\left( 2\,\,;-3 \right)$ và $ \overrightarrow{b}=\left( 1\,\,;\,\,m \right)$ cùng phương$ \Leftrightarrow \dfrac{1}{2}=\dfrac{m}{-3}\Leftrightarrow m=-\dfrac{3}{2}$ . Chọn đáp án D.
Câu 18.
Cho $ \overrightarrow{u}=\left( 2x-1\,;\,\,3 \right)$ , $ \overrightarrow{v}=\left( 1\,\,;\,\,x+2 \right)$ . Có hai giá trị $ {{x}_{1}},\,\,{{x}_{2}}$ của $ x$ để $ \overrightarrow{u}$ cùng phương với $ \overrightarrow{v}$ . Tính $ {{x}_{1}}. {{x}_{2}}$ .
[A]. $ \dfrac{5}{3}$ .
[B]. $ -\dfrac{5}{3}$ .
[C]. $ -\dfrac{5}{2}$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ \overrightarrow{u},\,\,\overrightarrow{v}$ cùng phương$ \Leftrightarrow \dfrac{2x-1}{1}=\dfrac{3}{x+2}$ (với $ x\ne -2$ )
$ \Leftrightarrow \left( 2x-1 \right)\left( x+2 \right)=3\Leftrightarrow 2{{x}^{2}}+3x-5=0$ . Vậy $ {{x}_{1}}. {{x}_{2}}=-\dfrac{5}{2}$ . Chọn đáp án C.
Câu 19.
Cho ba điểm $ A\left( 0\,\,;\,\,1 \right),B\left( 0\,\,;-2 \right),C\left( 3\,\,;\,\,0 \right)$ . Vẽ hình bình hành $ ABDC$ . Tìm tọa độ điểm $ D$ .
[A]. $ D\left( -3\,\,;\,\,3 \right)$ .
[B]. $ D\left( 3\,\,;-3 \right)$ .
[C]. $ D\left( 3\,\,;\,\,3 \right)$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ ABDC$ là hình bình hành $ \Leftrightarrow \overrightarrow{CD}=\overrightarrow{AB}\Leftrightarrow \left\{ \begin{array}{l}
{{x}_{D}}-3=0 \\
{{y}_{D}}-0=-3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{{x}_{D}}=3 \\
{{y}_{D}}=-3
\end{array} \right. $
Vậy $ D\left( 3\,\,;-3 \right)$ . Chọn đáp án B.
Câu 20.
Hai vectơ nào sau đây không cùng phương :
[A]. $ \overrightarrow{a}=\left( 3\,\,;\,\,5 \right)$ và $ \overrightarrow{b}=\left( -\dfrac{6}{7}\,\,;-\dfrac{10}{7} \right)$ .
[B]. $ \overrightarrow{c}$ và $ -4\overrightarrow{c}$ .
[C]. $ \overrightarrow{i}=\left( 1\,\,;\,\,0 \right)$ và $ \overrightarrow{m}=\left( -\dfrac{5}{2}\,\,;\,\,0 \right)$ .
[D]. $ \overrightarrow{m}=\left( -\sqrt{3}\,\,;\,\,0 \right)$ và $ \overrightarrow{n}=\left( 0\,\,;-\sqrt{3} \right)$ .
Hướng dẫn giải:
$ \overrightarrow{m}=\left( -\sqrt{3}\,\,;\,\,0 \right)$ và $ \overrightarrow{n}=\left( 0\,\,;-\sqrt{3} \right)$ . Ta có: $ {{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}=\left( -\sqrt{3} \right)\left( -\sqrt{3} \right)-0=3\ne 0$
Vậy $ \overrightarrow{m}$ và $ \overrightarrow{n}$ không cùng phương. Chọn đáp án D.
Câu 21.
Các điểm và các vectơ sau đây cho trong hệ trục $ \left( O\,\,;\,\overrightarrow{i},\overrightarrow{j} \right)$ (giả thiết $ m,\,\,n,\,\,p\,\,,q$ là những số thực khác $ 0$ ). Mệnh đề nào sau đây sai ?
[A]. $ \overrightarrow{a}=\left( m\,\,;\,\,0 \right)\Leftrightarrow \overrightarrow{a}\,\text{//}\,\overrightarrow{i}$ .
[B]. $ \overrightarrow{b}=\left( 0\,\,;\,\,n \right)\Leftrightarrow \overrightarrow{b}\,\text{//}\,\overrightarrow{j}$ .
[C]. Điểm $ A\left( n\,\,;\,\,p \right)\in x’Ox\Leftrightarrow n=0$ .
[D]. $ A\left( 0\,\,;\,\,p \right),B\left( q\,\,;\,\,p \right)$ thì$ AB\,\text{//}\,x’Ox$ .
Hướng dẫn giải:
$ A\left( n\,\,;\,\,p \right)\in x’Ox\Leftrightarrow p=0$ . Chọn đáp án C.
Câu 22.
Cho ba điểm $ A\left( 2\,\,;-4 \right),B\left( 6\,\,;\,\,0 \right),C\left( m\,\,;\,\,4 \right)$ . Định $ m$ để $ A,B,C$ thẳng hàng ?
[A]. $ m=10$ .
[B]. $ m=-6$ .
[C]. $ m=2$ .
[D]. Một số khác.
Hướng dẫn giải:
$ \overrightarrow{AB}=\left( 4\,\,;\,\,4 \right)\,\,;\,\,\overrightarrow{AC}=\left( m-2\,\,;\,\,8 \right). $
$ A,\,\,B,\,\,C$ thẳng hàng $ \Leftrightarrow \overrightarrow{AB},\,\,\overrightarrow{AC}$ cùng phương$ \Leftrightarrow \dfrac{m-2}{4}=\dfrac{8}{4}\Leftrightarrow m=10$ . Chọn đáp án A.
Câu 23.
Cho hai điểm \[A\left( {{x}_{A}}\,;\,{{y}_{A}} \right),B\left( {{x}_{B}}\,;\,{{y}_{B}} \right)\]. Tọa độ của điểm $ M$ mà $ \overrightarrow{MA}=k\overrightarrow{MB}\,\,\left( k\ne 1 \right)$ là :
[A]. $ \left\{ \begin{array}{l}
{{x}_{M}}=\dfrac{{{x}_{A}}+k. {{x}_{B}}}{1+k} \\
{{y}_{M}}=\dfrac{{{y}_{A}}+k. {{y}_{B}}}{1+k}
\end{array} \right. $ .
[B]. $ \left\{ \begin{array}{l}
{{x}_{M}}=\dfrac{{{x}_{A}}-{{x}_{B}}}{1-k} \\
{{y}_{M}}=\dfrac{{{y}_{A}}-{{y}_{B}}}{1-k}
\end{array} \right. $ .
[C]. $ \left\{ \begin{array}{l}
{{x}_{M}}=\dfrac{{{x}_{A}}-k. {{x}_{B}}}{1-k} \\
{{y}_{M}}=\dfrac{{{y}_{A}}-k. {{y}_{B}}}{1-k}
\end{array} \right. $ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ \overrightarrow{MA}=k\overrightarrow{MB}\Leftrightarrow \left\{ \begin{array}{l}
{{x}_{A}}-{{x}_{M}}=k\left( {{x}_{B}}-{{x}_{M}} \right) \\
{{y}_{A}}-{{y}_{M}}=k\left( {{y}_{B}}-{{y}_{M}} \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{{x}_{M}}=\dfrac{{{x}_{A}}-k. {{x}_{B}}}{1-k} \\
{{y}_{M}}=\dfrac{{{y}_{A}}-k. {{y}_{B}}}{1-k}
\end{array} \right. $ . Chọn đáp án C.
Câu 24.
Cho hai điểm $ M\left( 1\,\,;\,\,6 \right)$ và $ N\left( 6\,\,;\,\,3 \right)$ . Tìm điểm $ P$ mà $ \overrightarrow{PM}=2\overrightarrow{PN}$ .
[A]. $ P\left( 11\,\,;\,\,0 \right)$ .
[B]. $ P\left( 6\,\,;\,\,5 \right)$ .
[C]. $ P\left( 2\,\,;\,\,4 \right)$ .
[D]. Một đáp số khác.
Hướng dẫn giải:
$ \overrightarrow{PM}=2\overrightarrow{PN}\Leftrightarrow \left\{ \begin{array}{l}
{{x}_{P}}=\dfrac{1-2. 6}{1-2}=11 \\
{{y}_{P}}=\dfrac{6-2. 3}{1-2}=0
\end{array} \right. \Rightarrow P\left( 11\,\,;\,\,0 \right)$ . Chọn đáp án A.
Câu 25.
Cho hai điểm $ A\left( -3\,\,;\,\,1 \right)$ và $ B\left( -5\,\,;\,\,5 \right)$ . Tìm điểm $ M$ trên trục $ y’Oy$ sao cho $ MB-MA$ lớn nhất.
[A]. $ M\left( 0\,\,;-5 \right)$ .
[B]. $ M\left( 0\,\,;\,\,5 \right)$ .
[C]. $ M\left( 0\,\,;\,\,3 \right)$ .
[D]. $ M\left( 0\,\,;-6 \right)$ .
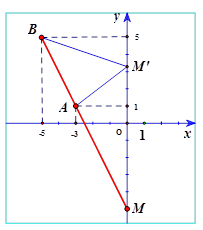
Hướng dẫn giải:
Lấy $ M\left( 0\,\,;\,\,y \right)\in y’Oy$ , với $ y$ bất kì.
Ta có : $ MB-MA\le AB$ ;
$ {{x}_{A}}. {{x}_{B}}=\left( -3 \right)\left( -5 \right)=15>0$ .
Vậy $ A,\,\,B$ nằm cùng bên đối với $ y’Oy$ (hình vẽ)
Do đó $ MB-MA$ lớn nhất khi $ MB-MA=AB$ , khi đó $ M,\,\,A,\,\,B$ thẳng hàng và $ M$ nằm ngoài đoạn $ AB$ .
$ \overrightarrow{MB}=\left( -5\,\,;\,\,5-y \right)\,\,;\,\,\overrightarrow{MA}=\left( -3\,\,;\,\,1-y \right). $
$ \overrightarrow{MB}=k\overrightarrow{MA}\Leftrightarrow \left\{ \begin{array}{l}
-5=-3k \\
5-y=k\left( 1-y \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
k=\dfrac{5}{3} \\
y=-5
\end{array} \right. $
Do đó $ M\left( 0\,\,;-5 \right)$ . Chọn đáp án A.