Bài toán tích của véc tơ với một số, trắc nghiệm toán 10
Câu 1.
Hai điểm \[M,N\] lần lượt chia đoạn $ AB$ thành $ 3$ đoạn bằng nhau. Tìm mệnh đề sai.
[A]. $ \overrightarrow{AM}=\overrightarrow{NB}. $
[B]. $ \overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AB}. $
[C]. $ \overrightarrow{AB}=3\overrightarrow{NM}. $
[D]. $ N$ là trung điểm $ MB. $

HD Ta có. $ \overrightarrow{AB}=-3\overrightarrow{NM}\Rightarrow $ Mệnh đề C sai. Chọn đáp án C.
Câu 2.
Cho $ \Delta ABC$ có trọng tâm $ G. $ Gọi $ I$ là trung điểm $ BC. $ Tìm mệnh đề đúng.
[A]. $ \overrightarrow{AI}=3\overrightarrow{IG}. $
[B]. \[\overrightarrow{IA}=\dfrac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right). \]
[C]. $ \overrightarrow{AG}=\dfrac{1}{3}\left( \overrightarrow{AB}+\overrightarrow{AC} \right). $
[D]. \[\overrightarrow{IG}=\dfrac{1}{4}\left( \overrightarrow{AB}+\overrightarrow{AC} \right). \]
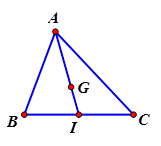
HD Ta có. $ \overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}=\dfrac{2}{3}. \dfrac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right)=\dfrac{1}{3}\left( \overrightarrow{AB}+\overrightarrow{AC} \right). $ Chọn đáp án C.
Câu 3.
Cho $ AB$ sao cho $ \overrightarrow{AM}=\dfrac{1}{6}\overrightarrow{AB}$ . Số $ k$ thỏa mãn $ \overrightarrow{MB}=k\overrightarrow{MA}$ là.
[A]. $ 5. $
[B]. $ -5. $
[C]. $ 4. $
[D]. Đáp án khác.
HD $ \overrightarrow{AM}=\dfrac{1}{6}\overrightarrow{AB}\Leftrightarrow \overrightarrow{AM}=\dfrac{1}{6}\overrightarrow{AM}+\dfrac{1}{6}\overrightarrow{MB}$ $ \Leftrightarrow \dfrac{5}{6}\overrightarrow{AM}=\dfrac{1}{6}\overrightarrow{MB}\Leftrightarrow \overrightarrow{MB}=-5\overrightarrow{MA}. $ Chọn đáp án B.
Câu 4.
Cho hai vectơ $ \vec{a}$ và $ \vec{b}$ không cùng phương. Tìm cặp vectơ cùng hướng với nhau trong các cặp vectơ sau.
[A]. \[\vec{c}=\dfrac{1}{2}\vec{a}+3\overrightarrow{b}\] và $ \overrightarrow{d}=2\vec{a}+7\overrightarrow{b}. $
[B]. $ \vec{u}=-\vec{a}+3\overrightarrow{b}$ và $ \vec{a}=\sqrt{5}\overrightarrow{b}. $
[C]. $ \vec{x}=\vec{a}+3\overrightarrow{b}$ và $ \vec{y}=\dfrac{1}{2}\vec{a}+\dfrac{3}{2}\overrightarrow{b}. $
[D]. $ \vec{m}=\vec{a}+2\overrightarrow{b}$ và $ \vec{n}=-\vec{a}-2\overrightarrow{b}. $
HD Xét $ \vec{c}$ và $ \vec{d}$ ta có. $ \dfrac{\dfrac{1}{2}}{2}\ne \dfrac{3}{7}\Rightarrow \vec{c},\vec{d}$ không cùng phương. Xét $ \vec{u}$ và $ \vec{a}$ ta có. $ \dfrac{0}{-1}\ne \dfrac{\sqrt{5}}{3}\Rightarrow \vec{u},\vec{a}$ không cùng phương. Xét $ \vec{x}$ và $ \vec{y}$ ta có. $ \dfrac{1}{\dfrac{1}{2}}=\dfrac{3}{\dfrac{3}{2}}=2>0\Rightarrow \vec{x}$ và $ \vec{y}$ cùng hướng. Chọn đáp án C.
Câu 5.
Cho $ \Delta ABC$ . Gọi $ M$ là điểm nằm trên đoạn $ BC$ sao cho $ \overrightarrow{MB}=-2\overrightarrow{MC}$ . Trong các biểu thức sau biểu thức nào đúng?
[A]. \[\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}. \]
[B]. \[\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}. \]
[C]. \[\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}. \]
[D]. \[\overrightarrow{AM}=-2\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}. \]
HD $ \overrightarrow{MB}=-2\overrightarrow{MC}\Leftrightarrow \overrightarrow{AB}-\overrightarrow{AM}=-2\left( \overrightarrow{AC}-\overrightarrow{AM} \right)$ $ \Leftrightarrow \overrightarrow{AB}+2\overrightarrow{AC}=3\overrightarrow{AM}\Leftrightarrow \overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}. $ Chọn đáp án C.
Câu 6.
Cho tam giác $ ABC$ có trọng tâm $ G,M$ là trung điểm của $ BC$ và $ O$ là điểm bất kì. Mệnh đề nào sau đây là sai?
[A]. $ \overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}. $
[B]. $ \overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OM}. $
[C]. $ \overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}. $
[D]. \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}. \]
HD $ G$ là trọng tâm của tam giác $ ABC$ Ta có. $ \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}. $ $ \Leftrightarrow \left( \overrightarrow{GO}+\overrightarrow{OA} \right)+\left( \overrightarrow{GO}+\overrightarrow{OB} \right)+\left( \overrightarrow{GO}+\overrightarrow{OB} \right)=\vec{0}$ $ \Leftrightarrow $ $ 3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ . $ \Rightarrow $ Mệnh đề ở C sai. Chọn đáp án C.
Câu 7.
Cho tam giác $ ABC$ có trọng tâm $ G$ và điểm $ M$ thỏa mãn $ 2\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}$ thì $ \overrightarrow{GM}$ bằng.
[A]. \[ – \dfrac{1}{6}\overrightarrow {BC} .\]
[B]. \[\dfrac{1}{6}\overrightarrow{CA}. \]
[C]. $ \dfrac{1}{6}\overrightarrow{AB}. $
[D]. Một vectơ khác
$ 2\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow 2\left( \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right)+\left( \overrightarrow{MC}-\overrightarrow{M}B \right)=\overrightarrow{0}\,\,\,\left( * \right)$ . Theo tính chất trọng tâm trong tam giác. $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG},\forall M$ $ \Rightarrow $ $ \left( * \right)\Leftrightarrow 2. 3\overrightarrow{MG}-\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{MG}=\dfrac{1}{6}\overrightarrow{BC}. $ Chọn đáp án A.
Câu 8.
Gọi $ G$ là trọng tâm của tam giác $ \Delta ABC$ , nếu điểm $ M$ thỏa hệ thức $ \overrightarrow{MA}+\overrightarrow{MB}+4\overrightarrow{MC}=\overrightarrow{0}$ thì vị trí của điểm $ M$ trong hình vẽ ?
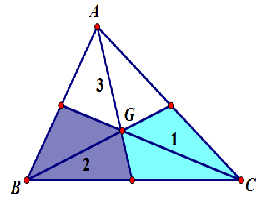
[A]. Miền 1
[B]. Miền 2
[C]. Miền 3
[D]. ở ngoài tam giác $ ABC$
HD $ \overrightarrow{MA}+\overrightarrow{MB}+4\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{MC}$ $ \Leftrightarrow 3\overrightarrow{MG}=-3\overrightarrow{MC}\Leftrightarrow \overrightarrow{MG}=-\overrightarrow{MC}\Leftrightarrow \overrightarrow{MG}=-\overrightarrow{MG}-\overrightarrow{GC}$ $ \Leftrightarrow \overrightarrow{GM}=\dfrac{1}{2}\overrightarrow{GC}. $ $ \Rightarrow $ $ M$ là trung điểm của $ GC$ . Chọn đáp án A.
Câu 9.
Cho tam giác $ \Delta ABC$ . Trên cạnh $ BC$ lấy điểm $ D$ sao cho $ \overrightarrow{BD}=\dfrac{1}{3}\overrightarrow{BC}$ , vectơ $ \overrightarrow{AD}$ bằng.
[A]. $ \dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}. $
[B]. $ \dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}. $
[C]. $ \overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}. $
[D]. $ \dfrac{5}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}. $
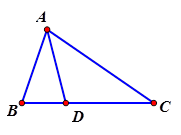
HD: \[\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{1}{3}\left( \overrightarrow{BA}+\overrightarrow{AC} \right)\] \[=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}. \] Chọn đáp án A.
Câu 10.
Cho hình bình hành $ ABCD$ . Nếu $ \overrightarrow{AB}=-2\overrightarrow{CI}$ thì câu nào sau đây đúng?
[A]. $ I\equiv D. $
[B]. $ I$ và \[D\] đối xứng nhau qua $ C. $
[C]. $ I\equiv B. $
[D]. $ I$ là trung điểm của $ CD. $
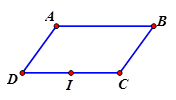
HD $ \overrightarrow{AB}=-2\overrightarrow{CI}\Leftrightarrow \overrightarrow{DC}=-2\overrightarrow{CI}\Leftrightarrow \overrightarrow{CI}=\dfrac{1}{2}\overrightarrow{CD}$ . Suy ra $ I$ là trung điểm của $ CD$ . Chọn đáp án D.
Câu 11.
Cho tứ giác lồi $ ABCD$ . Gọi $ M,N,I$ lần lượt là trung điểm của $ AB,CD,MN$ . Mệnh đề nào sau đây là sai ?
[A]. $ \overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IM}$
[B]. $ \overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IN}$
[C]. $ \overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}$
[D]. $ \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$
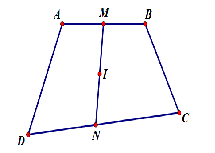
HD Mệnh đề A, B đúng do tính chất của trung điểm. Xét mệnh đề C. $ \overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IM}+2\overrightarrow{IN}=\overrightarrow{0}$ $ \Rightarrow $ Mệnh đề C đúng. Chọn đáp án D.
Câu 12.
Cho tứ giác $ ABCD$ và điểm $ G$ thỏa mãn $ \overrightarrow{GA}+\overrightarrow{GB}+2\overrightarrow{GC}+2\overrightarrow{GD}=\overrightarrow{0}$ . Gọi $ I,J$ lần lượt là các trọng tâm của cả tam giác $ ACD,BCD$ . $ \overrightarrow{GI}+\overrightarrow{GJ}$ bằng.
[A]. $ \overrightarrow{GA}. $
[B]. $ 3. \overrightarrow{GB}. $
[C]. $ 2. \overrightarrow{GC}. $
[D]. $ \overrightarrow{0}. $
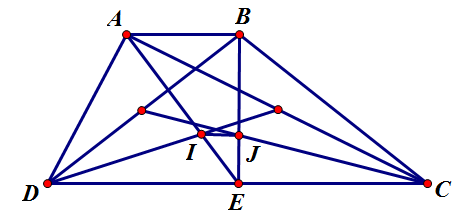
HD $ \overrightarrow{GA}+\overrightarrow{GB}+2\overrightarrow{GC}+2\overrightarrow{GD}=\left( \overrightarrow{GA}+\overrightarrow{GC}+\overrightarrow{GD} \right)+\left( \overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD} \right)$ $ =3\overrightarrow{GI}+3\overrightarrow{GJ}=\overrightarrow{0}$ . $ \Rightarrow $ $ G$ là trung điểm của \[IJ\]. Chọn đáp án D.
Câu 13.
Cho tứ giác $ ABCD$ và điểm $ G$ thỏa mãn $ \overrightarrow{GA}+\overrightarrow{GB}+2\overrightarrow{GC}+2\overrightarrow{GD}=\overrightarrow{0}$ . Gọi $ I,J$ lần lượt là các trọng tâm của cả tam giác $ ACD,BCD$ . Vectơ \[\overrightarrow{IJ}\] bằng.
[A]. $ \dfrac{1}{3}\overrightarrow{AB}. $
[B]. $ \dfrac{1}{3}\overrightarrow{BD}. $
[C]. $ \dfrac{1}{2}\overrightarrow{CD}. $
[D]. $ -\dfrac{1}{2}\overrightarrow{DB}. $
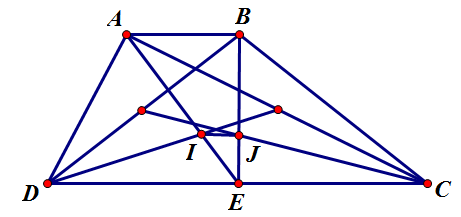
$ I,J$ là trọng tâm của các tam giác $ \Delta ACD,\Delta BCD$ .
\[ \Rightarrow \dfrac{{IE}}{{AE}} = \dfrac{{JE}}{{BE}} = \dfrac{1}{3} \Rightarrow IJ//AB \Rightarrow \dfrac{{{\rm{IJ}}}}{{AB}} = \dfrac{1}{3} \Rightarrow \overrightarrow {IJ} = \dfrac{1}{3}\overrightarrow {AB} \]
. Chọn đáp án A.
Câu 14.
Cho tam giác $ ABC$ . Gọi $ I,J,K$ là các điểm sao cho. $ \overrightarrow{CI}=2\overrightarrow{CB};\overrightarrow{CJ}=\dfrac{3}{4}\overrightarrow{CA};\overrightarrow{AK}=-2\overrightarrow{AB}$ . Ba đường thẳng $ AI,BJ,CK$ .
[A]. song song với nhau.
[B]. Đồng quy.
[C]. Trùng nhau.
[D]. Đáp án khác.
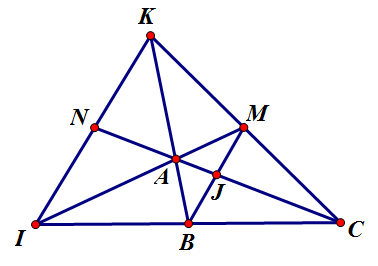
$ \overrightarrow{CI}=2\overrightarrow{CB}$ $ \Rightarrow $ $ B$ là trung điểm của $ CI$ . Vậy $ KB$ là trung tuyến của tam giác$ KIC$ , $ \overrightarrow{AK}=-2\overrightarrow{AB}$ nên $ A$ là trọng tâm của tam giác $ KIC$ .
Do đó $ AI$ cắt $ CK$ là trung điểm $ M$ của $ KC$ . Ta có. $ \overrightarrow{CJ}=\dfrac{3}{4}\overrightarrow{CA}=\dfrac{3}{4}. \dfrac{2}{3}\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{CN}$ .
Suy ra $ J$ cũng là trung điểm của $ CN$ . Do đó $ BJ$ đi qua $ M$ . Chọn đáp án B.
Câu 15.
Cho tam giác $ ABC$ có trọng tâm $ G,I$ là trung điểm của $ BC$ , $ {A}’$ là điểm đối xứng của $ A$ qua $ B;M$ là điểm tùy ý. Hỏi mệnh đề nào sau đây là đúng?
I. $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
II. $ \overrightarrow{MA}+\overrightarrow{M{A}’}+2\overrightarrow{MC}=2\overrightarrow{MB}+2\overrightarrow{MC}$
III. Nếu $ \overrightarrow{MA}+\overrightarrow{M{A}’}+2\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ thì $ M,I,G$ thẳng hàng.
[A]. Chỉ I và II.
[B]. Chỉ I và III.
[C]. Chỉ II và III.
[D]. Cả I, II, III.
HD I. Đúng (tính chất của trọng tâm tam giác) II. $ \overrightarrow{MA}+\overrightarrow{M{A}’}+2\overrightarrow{MC}=2\overrightarrow{MB}+2\overrightarrow{MC}=2\left( \overrightarrow{MB}+\overrightarrow{MC} \right)=4. \overrightarrow{MI}$ . Ta có. \[\overrightarrow{MA}+\overrightarrow{M{A}’}+2\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}. \] Suy ra $ M,I,G$ thẳng hàng. Vậy III đúng. Chọn đáp án D.
Câu 16.
Cho hình bình hành $ ABCD$ tâm $ O$ và điểm $ M$ thỏa mãn hệ thức $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=k\overrightarrow{MD}$ (trong đó $ k$ là một số thực khác 3). Khi $ k$ thay đổi $ M$ luôn nằm trên một đường thẳng.
[A]. $ DA. $
[B]. $ DC. $
[C]. $ BD. $
[D]. $ AC. $
HD $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=k\overrightarrow{MD}\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\left( k+1 \right)\overrightarrow{MD}$ . Suy ra. $ 4\overrightarrow{MO}=\left( k+1 \right)\overrightarrow{MD}\Leftrightarrow 4\overrightarrow{MO}=\left( k+1 \right)\overrightarrow{MO}+\left( k+1 \right)\overrightarrow{OD}$ . \[\Leftrightarrow \left( k-3 \right)\overrightarrow{MO}=\left( k+1 \right)\overrightarrow{OD}\Leftrightarrow \overrightarrow{OM}=-\dfrac{\left( k+1 \right)}{\left( k-3 \right)}\overrightarrow{OD}\] Do đó, nếu $ k\ne -1;k\ne 3$ thì $ \overrightarrow{OM}$ cùng phương $ \overrightarrow{OD}$ hay $ O,M,D$ thẳng hàng. Từ đó, suy ra $ M\in OD$ hay $ M\in BD$ . Chọn đáp án C.
Câu 17.
Cho tứ giác $ ABCD$ . Gọi $ G$ là trọng tâm của tam giác $ ABC$ và $ O$ là trung điểm của $ BC$ . Vẽ $ \overrightarrow{OM}=\dfrac{1}{2}\overrightarrow{DA}$ . Ba điểm nào sau đây thẳng hàng.
[A]. $ M,G,D. $
[B]. $ M,G,A. $
[C]. $ M,G,B. $
[D]. $ M,G,C. $
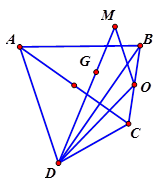
G là trọng tâm của tam giác $ ABC$ , ta có.
$ \overrightarrow{DG}=\dfrac{1}{3}\left( \underbrace{\overrightarrow{DA}}_{2\overrightarrow{OM}}+\underbrace{\overrightarrow{DB}+\overrightarrow{DC}}_{\overrightarrow{OM}} \right)=\dfrac{2}{3}\left( \overrightarrow{DO}+\overrightarrow{OM} \right)=\dfrac{2}{3}\overrightarrow{DM}$
Chọn đáp án A.
Câu 18.
Cho tam giác $ ABC$ có trung tuyến $ AD$ . Xét các điểm $ M,N,P$ cho bởi. $ \overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}$ , $ \overrightarrow{AN}=\dfrac{1}{4}\overrightarrow{AC}$ , $ \overrightarrow{AP}=t\overrightarrow{AD}$ . Tìm $ t$ để ba điểm $ M,N,P$ thẳng hàng.
[A]. $ t=\dfrac{1}{6}. $
[B]. $ t=\dfrac{1}{3}. $
[C]. $ t=\dfrac{1}{4}. $
[D]. Đáp án khác.
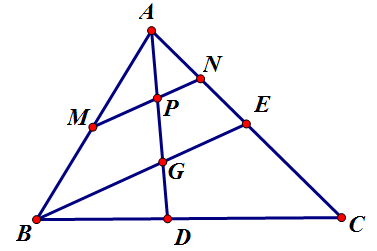
HD Gọi $ E$ là trung điểm của$ AC$ , ta có. $ AN=\dfrac{1}{2}\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}$ . Vậy $ MN$ //$ BE$ và$ G$ là trọng tâm của tam giác $ ABC$ . Ta có. $ \overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}$ . $ M,N,P$ thẳng hàng $ \Leftrightarrow $ $ P$ là trung điểm của $ AG$ . Vậy $ \overrightarrow{AP}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AD}$ . Chọn đáp án B.
Câu 19.
Cho hình bình hành $ ABCD$ , tâm $ O$ và $ I$ là trung điểm của$ CD$ . Tập hợp những điểm $ M$ mà $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=2. \overrightarrow{MI}$ là.
[A]. Chỉ gồm một điểm trên cạnh $ CD. $
[B]. Chỉ gồm một điểm trên cạnh $ AB. $
[C]. Chỉ gồm điểm $ O. $
[D]. Là một đường thảng đi qua hai điểm $ A,B. $
HD $ \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=2. \overrightarrow{MI}\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MI}=2\overrightarrow{MI}\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$ . Vậy $ M$ là trung điểm của $ AB$ . Chọn đáp án B.
Câu 20.
Cho tam giác$ ABC$ . Tập hợp những điểm$ M$ mà $ \left| \overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC} \right|=\left| \overrightarrow{MB}+\overrightarrow{MC} \right|$ là đường tròn có.
[A]. Tâm$ I$ , bán kính \[CJ\] ($ I$ là trung điểm của $ BC$ )
[B]. Tâm$ J$ , bán kính $ BI$ ($ J$ là trung điểm của$ AB$ )
[C]. Tâm$ B$ , bán kính $ \dfrac{AB}{2}$
[D]. Tâm$ C$ , bán kính $ \dfrac{AC}{2}$
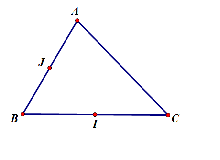
HD Gọi$ I$ là trung điểm $ BC$ ,$ J$ là trung điểm của$ AB$ $ \left| \overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC} \right|=\left| \overrightarrow{MB}+\overrightarrow{MC} \right|\Leftrightarrow \left| \left( \overrightarrow{MA}-\overrightarrow{MC} \right)+\left( \overrightarrow{MB}-\overrightarrow{MC} \right) \right|=\left| \overrightarrow{MB}+\overrightarrow{MC} \right|$ \[\Leftrightarrow \left| \overrightarrow{CA}+\overrightarrow{CB} \right|=\left| \overrightarrow{MB}+\overrightarrow{MC} \right|\Leftrightarrow 2\left| \overrightarrow{CJ} \right|=2\left| \overrightarrow{MI} \right|\Leftrightarrow IM=CJ\] (Tập hợp các điểm$ M$ là đường tròn tâm$ I$ , bán kính$ CJ$ . Chọn đáp án A.