Bài toán tổng, hiệu các véc tơ, trắc nghiệm toán 10
Câu 1.
Cho ba điểm $ A,B,C$ phân biệt thẳng hàng. Câu nào sau đây đúng?
[A]. Nếu $ B$ là trung điểm của $ AC$ thì $ \overrightarrow{AB}=\overrightarrow{CB}. $
[B]. Nếu điểm $ B$ nằm giữa $ A$ và $ C$ thì $ \overrightarrow{BC},\overrightarrow{BA}$ ngược hướng.
[C]. Nếu $ \left| \overrightarrow{AB} \right|>\left| \overrightarrow{AB} \right|$ thì B nằm trên đoạn$ AC$ .
[D]. $ \left| \overrightarrow{CA}+\overrightarrow{AB} \right|=\left| \overrightarrow{CA} \right|+\left| \overrightarrow{AB} \right|. $
HD B nằm giữa $ A,C$ thì hai điểm $ A,C$ nằm hai phía so với $ B$ nên thì $ \overrightarrow{BC},\overrightarrow{BA}$ ngược hướng. Chọn đáp án B.
Câu 2.
Mệnh đề nào sau đây là sai.
[A]. $ \overrightarrow{AB}=\overrightarrow{AC}\Rightarrow B\equiv C. $
[B]. Với mọi điểm $ A,B,C$ bất kì ta luôn có. $ \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}. $
[C]. \[\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{0}\] khi và chỉ khi B là trung điểm $ AC$ .
[D]. Tứ giác \[ABCD\]là hình bình hành khi và chỉ khi $ \overrightarrow{AB}=\overrightarrow{CD}. $ `
HD Tứ giác \[ABCD\]là hình bình hành suy ra $ \overrightarrow{AB}=\overrightarrow{DC}$ Chọn đáp án D.
Câu 3.
Cho tam giác $ ABC$ có trực tâm $ H$ và nội tiếp trong đường tròn tâm $ O$ . $ {B}’$ là điểm đối xứng của $ B$ qua $ O$ . Mệnh đề nào sau đây là sai?
[A]. $ \overrightarrow{AH},\overrightarrow{{B}’C}$ cùng phương.
[B]. $ \overrightarrow{CH},\overrightarrow{{B}’A}$ cùng phương.
[C]. \[AHC{B}’\] là hình bình hành.
[D]. $ \overrightarrow{HB}=\overrightarrow{HA}+\overrightarrow{HC}. $
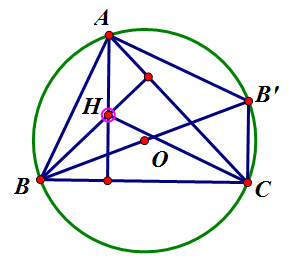
HD Vì $ \text{H}$ là trực tâm của tam giác \[\text{ABC}\] nên tứ giác \[\text{AHC{B}’}~\] là hình bình hành. Do đó, các câu A, B, C đúng. $ \overrightarrow{H{B}’}=\overrightarrow{HA}+\overrightarrow{HC}$ nên câu D sai. Chọn đáp án D.
Câu 4.
Cho tam giác $ ABC$ câu nào sau đây là đúng?
[A]. $ \overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}. $
[B]. $ \overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}=\overrightarrow{0}. $
[C]. $ \overrightarrow{AC}+\overrightarrow{BA}=\overrightarrow{CB}. $
[D]. $ \overrightarrow{AB}+\overrightarrow{AC}>\overrightarrow{BC}. $
HD $ \overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow \left( \overrightarrow{CA}+\overrightarrow{AB} \right)+\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}$ Chọn đáp án B.
Câu 5.
Cho tam giác $ ABC$ cân tại đỉnh $ A$ . Mệnh đề nào sau đây sai?
[A]. $ \overrightarrow{AB}=\overrightarrow{AC}$
[B]. \[\left| \overrightarrow{AB}-\overrightarrow{AC} \right|=\left| \overrightarrow{BC} \right|\]
[C]. \[\left| \overrightarrow{BC}+\overrightarrow{AB} \right|=\left| \overrightarrow{AB} \right|\]
[D]. $ \left| \overrightarrow{AB} \right|=\left| \overrightarrow{AC} \right|$
HD $ \overrightarrow{AB},\overrightarrow{AC}$ là hai vectơ không cùng phương nên $ \overrightarrow{AB}\ne \overrightarrow{AC}$ . Chọn đáp án A.
Câu 6.
Cho tam giác $ ABC$ đều cạnh a. Khi đó $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|$ bằng.
[A]. $ a\sqrt{3}. $
[B]. $ \dfrac{a\sqrt{3}}{2}. $
[C]. $ 2a. $
[D]. Một đáp án khác.
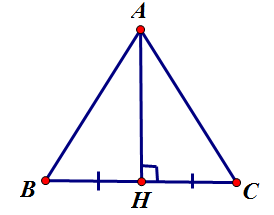
HD Gọi \[H\] là trung điểm của $ BC$ , $ \Rightarrow AH\bot BC. $ Suy ra. $ AH=\dfrac{BC\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}$ . Ta lại có. $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\left| 2\overrightarrow{AH} \right|=2. \dfrac{a\sqrt{3}}{2}=a\sqrt{3}$ Chọn đáp án A.
Câu 7.
Cho tam giác đều $ ABC$ cạnh a. Khi đó $ \left| \overrightarrow{AB}-\overrightarrow{AC} \right|$ bằng.
[A]. $ 0. $
[B]. $ \dfrac{a}{2}. $
[C]. $ a. $
[D]. $ a\sqrt{3}. $
HD $ \left| \overrightarrow{AB}-\overrightarrow{AC} \right|=\left| \overrightarrow{CB} \right|=a$ Chọn đáp án C.
Câu 8.
Cho bốn vectơ $ \overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{d}$ bất kì. Câu nào sau đây sai ?
[A]. $ \left( \overrightarrow{a}+\overrightarrow{b} \right)+\left( \overrightarrow{c}+\overrightarrow{d} \right)=\left( \overrightarrow{a}+\overrightarrow{d} \right)+\left( \overrightarrow{b}+\overrightarrow{c} \right). $
[B]. $ \left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|\Leftrightarrow \overrightarrow{a}=\pm \,\,\,\overrightarrow{b}. $
[C]. $ \overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\Rightarrow \overrightarrow{b}=\overrightarrow{a}-\overrightarrow{c}. $
[D]. $ \overrightarrow{a}+\left( -\overrightarrow{a} \right)=\overrightarrow{0}. $
HD Đáp án$ B$ sai. Ví dụ. khi tam giác $ ABC$ cân tại đỉnh $ A$ ta có $ \left| \overrightarrow{AB} \right|=\left| \overrightarrow{AC} \right|$ nhưng $ \overrightarrow{AB}\ne \pm \overrightarrow{AC}$ . Chọn đáp án B.
Câu 9.
Cho tam giác $ ABC$ vuông cân tại $ A$ có $ AB=6$ . Độ dài của vectơ $ \overrightarrow{BC}-\overrightarrow{BA}$ bằng.
[A]. $ 6\sqrt{2}. $
[B]. $ 6. $
[C]. $ 3\sqrt{2}. $
[D]. $ 3. $
HD $ \left| \overrightarrow{BC}-\overrightarrow{BA} \right|=\left| \overrightarrow{AC} \right|=6$ . Chọn đáp án B.
Câu 10.
Cho hình bình hành $ ABCD$ . Vectơ $ \overrightarrow{BC}-\overrightarrow{AB}$ bằng vectơ.
[A]. $ \overrightarrow{AC}. $
[B]. $ \overrightarrow{DB}. $
[C]. $ \overrightarrow{BD}. $
[D]. $ \overrightarrow{CA}. $
HD $ \overrightarrow{BC}-\overrightarrow{AB}=\overrightarrow{BC}+\overrightarrow{BA}=\overrightarrow{BD}$ . Chọn đáp án C.
Câu 11.
Cho hình chữ nhật $ ABCD$ . Biểu thức $ \overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}$ bằng.
[A]. $ \overrightarrow{AB}. $
[B]. $ \overrightarrow{AC}. $
[C]. $ \overrightarrow{DB}. $
[D]. $ \overrightarrow{0}. $
HD $ \overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{CD}+\overrightarrow{DC}=\overrightarrow{0}$ . Chọn đáp án D.
Câu 12.
Cho hình bình hành\[ABCD\]. Gọi O là điểm bất kỳ trên đường chéo BD sao cho $ OB>OD. $ Tìm mệnh đề đúng.
[A]. $ \overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OC}. $
[B]. $ \overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OD}. $
[C]. $ \overrightarrow{OB}+\overrightarrow{OA}=\overrightarrow{OC}+\overrightarrow{OD}. $
[D]. $ \overrightarrow{AB}-\overrightarrow{OD}+\overrightarrow{AD}-\overrightarrow{BO}=\overrightarrow{0}. $
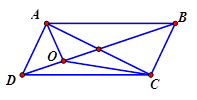
HD $ \overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OC}\Leftrightarrow \overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OC}-\overrightarrow{OD}\Leftrightarrow \overrightarrow{AB}=\overrightarrow{DC}$ (đúng) $ \overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OD}\Leftrightarrow \overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OD}-\overrightarrow{OC}\Leftrightarrow \overrightarrow{AB}=\overrightarrow{CD}$ sai. $ \overrightarrow{OB}+\overrightarrow{OA}=\overrightarrow{OC}+\overrightarrow{OD}\Leftrightarrow \overrightarrow{OB}-\overrightarrow{OC}=\overrightarrow{OD}-\overrightarrow{OA}\Leftrightarrow \overrightarrow{CB}=\overrightarrow{AD}$ sai. $ \overrightarrow{AB}-\overrightarrow{OD}+\overrightarrow{AD}-\overrightarrow{BO}=\overrightarrow{0}. $ $ \Leftrightarrow \left( \overrightarrow{AB}+\overrightarrow{AD} \right)+\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}. $ $ \Leftrightarrow \overrightarrow{AC}+\overrightarrow{DB}=\vec{0}$ sai. Chọn đáp án A.
Câu 13.
Cho $ \Delta ABC$ có G là trọng tâm. Tìm mệnh đề đúng.
[A]. $ \overrightarrow{GA}+\overrightarrow{GB}=\overrightarrow{GC}. $
[B]. $ \overrightarrow{GA}+\overrightarrow{GC}=\overrightarrow{GB}. $
[C]. $ \overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{AG}. $
[D]. $ \overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GA}. $
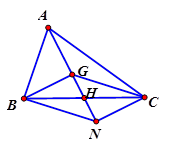
HD Gọi $ H$ là trung điểm của $ BC. $ Gọi \[N\] là điểm để $ BGCN$ là hình bình hành. $ \overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GN}. $ Ta có. $ GN=2GH=AG\Rightarrow \overrightarrow{GN}=\overrightarrow{AG}$ $ \Rightarrow $ $ \overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{AG}. $ Chọn đáp án C.
Câu 14.
Cho lục giác ABCDEF. Tìm mệnh đề đúng
[A]. $ \overrightarrow{AF}-\overrightarrow{DA}+\overrightarrow{FC}-\overrightarrow{DC}=\overrightarrow{0}. $
[B]. $ \overrightarrow{BE}-\overrightarrow{AE}+\overrightarrow{AD}-\overrightarrow{BD}=\overrightarrow{0}. $
[C]. $ \overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}. $
[D]. \[\overrightarrow{EB}+\overrightarrow{FC}+\overrightarrow{AD}=\overrightarrow{EC}+\overrightarrow{FD}+\overrightarrow{EA}. \]
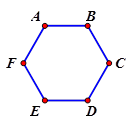
HD $ \overrightarrow{AF}-\overrightarrow{DA}+\overrightarrow{FC}-\overrightarrow{DC}=\overrightarrow{0}\Leftrightarrow $ $ \left( \overrightarrow{AF}+\overrightarrow{FC} \right)+\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{0}. $ $ \Leftrightarrow \overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{DC}$ sai $ \Rightarrow A$ sai. $ \overrightarrow{BE}-\overrightarrow{AE}+\overrightarrow{AD}-\overrightarrow{BD}=\overrightarrow{0}$ $ \Leftrightarrow \overrightarrow{EA}-\overrightarrow{EB}+\overrightarrow{AD}+\overrightarrow{DB}=\vec{0}$ $ \Leftrightarrow \overrightarrow{BA}+\overrightarrow{AB}=\vec{0}$ đúng. Chọn đáp án B.
Câu 15.
Nếu $ \Delta ABC$ có $ \left| \overrightarrow{CA}+\overrightarrow{CB} \right|=\left| \overrightarrow{CA}-\overrightarrow{CB} \right|$ thì $ \Delta ABC$ là.
[A]. Tam giác vuông tại A.
[B]. Tam giác cân tại A.
[C]. Tam giác vuông tại
[D]. Tam giác đều.
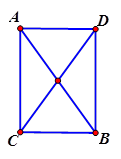
HD Gọi $ D$ là điểm để tứ giác $ ACBD$ là hình bình hành. $ \left| \overrightarrow{CA}+\overrightarrow{CB} \right|=\left| \overrightarrow{CA}-\overrightarrow{CB} \right|\Leftrightarrow \left| \overrightarrow{CD} \right|=\left| \overrightarrow{BA} \right|\Leftrightarrow CD=AB$ $ \Rightarrow $ hình bình hành $ ACBD$ có hai đường chéo bằng nhau. $ \Rightarrow $ $ ACBD$ là hình chữ nhật. $ \Rightarrow \Delta ABC$ vuông tại $ C. $ Chọn đáp án C.
Câu 16.
Cho hai vectơ $ \vec{a}$ và $ \vec{b}$ khác $ \vec{a}$ và $ \vec{b}$ khác $ \overrightarrow{0}$ sao cho $ \vec{a}+\vec{b}=\overrightarrow{0}$ . Dựng $ \overrightarrow{OA}=\vec{a},\overrightarrow{OB}=\vec{b}$ . Tìm mệnh đề đúng
[A]. $ \overrightarrow{OA}=\overrightarrow{AB}. $
[B]. O là trung điểm AB.
[C]. $ \overrightarrow{OA}=\overrightarrow{OB}. $
[D]. $ A\equiv B. $
HD $ \vec{a}+\vec{b}=\overrightarrow{0}$ $ \Rightarrow \vec{a},\vec{b}$ là hai vectơ đối nhau. $ \Rightarrow O$ là trung điểm của $ AB. $ Chọn đáp án B.
Câu 17.
Cho đều cạnh bằng 5cm. Gọi H là trung điểm BC. Tìm mệnh đề sai.
[A]. $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|=5\sqrt{3}. $
[B]. $ \left| \overrightarrow{HA}-\overrightarrow{HB} \right|=5. $
[C]. $ \left| \overrightarrow{CA}+\overrightarrow{CH} \right|=14. $
[D]. $ \left| \overrightarrow{HA}+\overrightarrow{HC} \right|=5. $
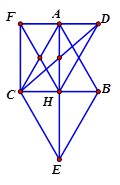
HD Gọi $ D,E,F$ lần lượt là các điểm để các tứ giác $ ACHD,ACEB,AHCF$ là hình bình hành. $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\left| \overrightarrow{AE} \right|=AE=2AH=2. \dfrac{5\sqrt{3}}{2}=5\sqrt{3}\Rightarrow A$ đúng. $ \left| \overrightarrow{HA}-\overrightarrow{HB} \right|=\left| \overrightarrow{BA} \right|=BA=5\Rightarrow B$ đúng. $ \left| \overrightarrow{CA}+\overrightarrow{CH} \right|=\left| \overrightarrow{CD} \right|=CD<CA+AD=5+\dfrac{5}{2}<14\Rightarrow C$ sai. $ \left| \overrightarrow{HA}+\overrightarrow{HC} \right|=\left| \overrightarrow{HF} \right|=HF=AC=5\Rightarrow D$ đúng. Chọn đáp án C.
Câu 18.
Cho $ \Delta ABC$ có trung tuyến CI. Gọi M, N lần lượt nằm trên BC sao cho $ BM=MN=NC. $ AN cắt IC tại E. Tìm mệnh đề đúng.
[A]. $ \overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}=\vec{0}. $
[B]. $ \overrightarrow{EI}+\overrightarrow{EC}=\vec{0}. $
[C]. $ \overrightarrow{EA}+\overrightarrow{EN}=\vec{0}. $
[D]. $ \overrightarrow{MI}+\overrightarrow{ME}=\overrightarrow{MC}. $
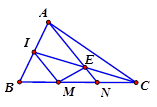
HD IM là đường trung bình $ \Delta BAN$ $ \Rightarrow IM//EN$ $ \Delta CMI$ có N là trung điểm MC, NE // IM $ \Rightarrow $ E là trung điểm IC $ \Rightarrow $ $ \overrightarrow{EI}+\overrightarrow{EC}=\overrightarrow{0}$ Chọn đáp án B.
Câu 19.
Cho $ \Delta ABC$ đều cạnh 2cm. Gọi H là trung điểm cạnh BC. Tìm các mệnh đề sai.
[A]. $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2\sqrt{3}. $
[B]. $ \left| \overrightarrow{HB}+\overrightarrow{HA} \right|=2. $
[C]. $ \left| \overrightarrow{HA}-\overrightarrow{HC} \right|=2. $
[D]. $ \left| \overrightarrow{AH}+\overrightarrow{AC} \right|=10. $
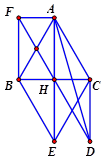
HD Gọi $ D,E,F$ lần lượt là các điểm để $ AHDC,ABEC,AHBF$ là các hình bình hành. Ta có. $ \left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\left| \overrightarrow{AE} \right|=AE=2AH=2. \dfrac{2. \sqrt{3}}{2}=2\sqrt{3}\Rightarrow A$ đúng. $ \left| \overrightarrow{HB}+\overrightarrow{HA} \right|=HF$ mà $ AHBF$ là hình chữ nhật $ \Rightarrow HF=AB=2\Rightarrow B$ đúng. $ \left| \overrightarrow{HA}-\overrightarrow{HC} \right|=CA=2\Rightarrow C$ đúng. $ \left| \overrightarrow{AH}+\overrightarrow{AC} \right|=\left| \overrightarrow{AD} \right|=AD<AC+CD=2+\sqrt{3}<10$ $ \Rightarrow D$ sai. Chọn đáp án D.
Câu 20.
Cho tam giác đều $ ABC$ cạnh $ a$ . Tập hợp các điểm $ M$ sao cho $ \left| \overrightarrow{MA}-\overrightarrow{MB} \right|=\overrightarrow{MC}$ là.
[A]. Một đường thẳng.
[B]. Một đường tròn tâm $ B. $
[C]. Một đường tròn tâm $ C. $
[D]. Một đường tròn tâm $ A. $
HD \[\left| \overrightarrow{MA}-\overrightarrow{MB} \right|=\left| \overrightarrow{MC} \right|\Leftrightarrow CM=BA=a\] không đổi. Tập hợp các điểm $ M$ là đường tròn tâm $ C$ , bán kính a. Chọn đáp án C.