Các định nghĩa véc-tơ, trắc nghiệm toán 10
Câu 1.
Các khẳng định sau khẳng định nào đúng ?
[A]. Vectơ là một đường thẳng.
[B]. Vectơ là một đoạn thẳng có hướng.
[C]. Vectơ là một trục.
[D]. Vectơ là một đoạn thẳng.
HD Chọn đáp án B.
Câu 2.
Gọi $$O$$ là trung điểm của $$AB. $$ Khẳng định nào sau đây là đúng?
[A]. $$\overrightarrow{OA}=\overrightarrow{OB}. $$
[B]. $$\left| \overrightarrow{OA} \right|=-\left| \overrightarrow{OB} \right|. $$
[C]. $$\overrightarrow{OA}=\overrightarrow{BO}. $$
[D]. $$\overrightarrow{AO}=\overrightarrow{AB}. $$
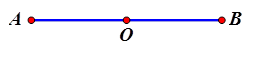
HD $$\overrightarrow{OA}=-\overrightarrow{OB}\Rightarrow A$$ sai. $$OA=OB\Rightarrow B$$ sai. $$\overrightarrow{AO}\ne \overrightarrow{AB}\Rightarrow D$$ sai. Chọn đáp án C.
Câu 3.
Tứ giác $$ABCD$$ có $$\overrightarrow{AB}=\overrightarrow{DC}$$ thì tứ giác $$ABCD$$
[A]. là hình thang.
[B]. là hình bình hành.
[C]. là hình thoi.
[D]. là hình chữ nhật.
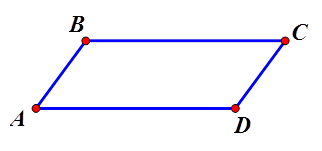
HD Chọn đáp án B.
Câu 4.
Cho đoạn thẳng AB và điểm O bất kỳ. Dựng $$\overrightarrow{OC}=\overrightarrow{AB}$$thì
[A]. có duy nhất điểm $$C. $$
[B]. có vô số điểm $$C. $$
[C]. không có điểm $$C. $$
[D]. có hai điểm $$C. $$
HD $$\overrightarrow{OC}=\overrightarrow{AB}\Rightarrow OCBA$$là hình bình hành. $$\Rightarrow $$ Chọn đáp án A.
Câu 5.
Cho tứ giác $$ABCD,$$ có bao nhiêu vectơ khác vectơ $$\vec{0}$$ mà có gốc và ngọn được lấy từ các điểm $$A,B,C,D$$?
[A]. $$4. $$
[B]. $$8. $$
[C]. $$12. $$
[D]. $$16. $$
HD Mỗi đỉnh sẽ ghép với $$3$$ đỉnh còn lại để tạo thành vectơ. $$\Rightarrow $$ Số vectơ tạo thành. $$4. 3=12$$ vectơ. Chọn đáp án C.
Công thức tổng quát, $$n$$ điểm phân biệt, số vectơ $$\ne \vec{0}$$ có điểm đầu và điểm cuối từ $$n$$ điểm đã cho bằng. $$n\left( n-1 \right)$$ vectơ.
Câu 6.
Cho tam giác$$ABC,$$ có bao nhiêu vectơ khác vectơ $$\vec{0}$$ mà có gốc và ngọn được lấy từ các điểm $$A,B,C$$?
[A]. $$3. $$
[B]. $$4. $$
[C]. $$6. $$
[D]. $$8. $$
HD Áp dụng công thức. $$n\left( n-1 \right)=3. 2=6$$ vectơ. Chọn đáp án C.
Câu 7.
Cho lục giác $$ABCDEF$$, có bao nhiêu vectơ khác vectơ $$\vec{0}$$ mà có gốc và ngọn được lấy từ các điểm $$A,B,C,D,E,F$$?
[A]. $$12. $$
[B]. $$24. $$
[C]. $$28. $$
[D]. $$30. $$
HD Áp dụng công thức. $$n\left( n-1 \right)=6. 5=30$$ vectơ. Chọn đáp án D.
Câu 8.
Cho hình bình hành \[ABCD\] tâm O. Tìm mệnh đề đúng.
[A]. \[\overrightarrow{AB}=\overrightarrow{CD}. \]
[B]. \[\overrightarrow{DO}=\overrightarrow{CO}. \]
[C]. \[\overrightarrow{OA}=\overrightarrow{OC}. \]
[D]. \[\overrightarrow{CB}=\overrightarrow{DA}. \]
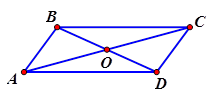
HD \[\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow A\] sai. \[\overrightarrow{DO},\overrightarrow{CO}\]không cùng phương $$\Rightarrow B$$ sai. \[\overrightarrow{OA},\overrightarrow{OC}\]ngược chiều $$\Rightarrow C$$ sai. Chọn đáp án D.
Câu 9.
Cho $$\Delta ABC$$ vuông tại A có $$AB=1,BC=2AB. $$ Dựng hình bình hành \[ABCD\]. Xác định $$\left| \overrightarrow{BD} \right|$$.
[A]. $$\sqrt{3}. $$
[B]. $$\sqrt{7}. $$
[C]. $$\sqrt{6}. $$
[D]. $$2\sqrt{2}. $$
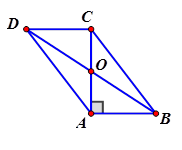
HD Gọi $$O=AC\cap BD\Rightarrow BD=2OB. $$ $$BC=2AB=2\Rightarrow AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=\sqrt{3}. $$ $$\Rightarrow OA=\dfrac{1}{2}AC=\dfrac{\sqrt{3}}{2}. $$ $$\Rightarrow BO=\sqrt{A{{O}^{2}}+A{{B}^{2}}}=\sqrt{\dfrac{3}{4}+1}=\dfrac{\sqrt{7}}{2}. $$ $$\Rightarrow BD=2BO=\sqrt{7}. $$ Chọn đáp án B.
Câu 10.
Cho hình thoi \[ABCD\] có $$\widehat{A}={{60}^{0}}$$,\[AB\text{ }=\text{ }1\]. Độ dài của $$\overrightarrow{AC}$$ là.
[A]. $$2. $$
[B]. $$\sqrt{3}. $$
[C]. $$\dfrac{1}{3}. $$
[D]. $$\dfrac{\sqrt{3}}{2}. $$
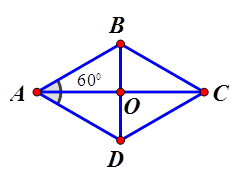
HD Gọi $$O=AC\cap BD\Rightarrow O$$ là trung điểm $$AC. $$ $$\Rightarrow AO=\dfrac{1}{2}AC. $$ Ta có. $$ABD$$ là tam giác đều cạnh bằng $$1\Rightarrow AO=\dfrac{\sqrt{3}}{2}\Rightarrow AC=\sqrt{3}. $$ Chọn đáp án B.
Câu 11.
Cho hình bình hành \[ABCD\]. Dựng,\[\overrightarrow{BR}=\overrightarrow{CB},\overrightarrow{RQ}=\overrightarrow{AB},\overrightarrow{QP}=\overrightarrow{BC},\overrightarrow{PS}=\overrightarrow{BA}\]. Tìm mệnh đề đúng.
[A]. \[\left| \overrightarrow{RA} \right|=\left| \overrightarrow{AC} \right|. \]
[B]. \[\overrightarrow{BS}=\overrightarrow{RP}. \]
[C]. \[\overrightarrow{AS}=\overrightarrow{AC}. \]
[D]. \[\overrightarrow{BS}=\overrightarrow{0}. \]
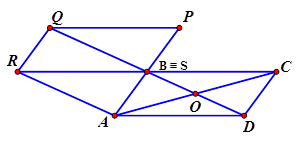
HD \[\overrightarrow{BR}=\overrightarrow{CB}=\overrightarrow{DA}\Rightarrow ADBR\]là hình bình hành. $$\Rightarrow RA=BD\ne AC\Rightarrow A$$ sai. $$B\equiv S\Rightarrow \overrightarrow{BS}=\vec{0}$$ Chọn đáp án D.
Câu 12.
Cho \[ABCDEF\]là lục giác đều tâm O. Đẳng thức nào sau đây đúng.
[A]. \[\overrightarrow{AB}=\overrightarrow{EF}. \]
[B]. \[\overrightarrow{BO}=\overrightarrow{EO}. \]
[C]. \[\overrightarrow{BC}=\overrightarrow{FE}. \]
[D]. \[\overrightarrow{OA}=\overrightarrow{OC}. \]
HD Chọn đáp án C.
Câu 13.
Cho lục giác đều \[ABCDEF\] tâm O. Số các vectơ bằng $$\overrightarrow{OC}$$ có điểm đầu và cuối là đỉnh của lục giác là.
[A]. $$2. $$
[B]. $$3. $$
[C]. $$4. $$
[D]. $$6. $$
HD Vectơ bằng $$\overrightarrow{OC}$$ có điểm đầu và cuối là đỉnh của lục giác là. $$\overrightarrow{AB},\overrightarrow{ED}\Rightarrow $$ có $$2$$ vectơ thỏa mãn. Chọn đáp án A.
Câu 14.
Cho $$\overrightarrow{AB}$$ ≠ $$\vec{0}$$ và một điểm C, có bao nhiêu điểm D thỏa mãn. $$\left| \overrightarrow{AB} \right|=\left| \overrightarrow{C\text{D}} \right|$$
[A]. $$0. $$
[B]. $$1. $$
[C]. $$2. $$
[D]. Vô số.
HD $$\left| \overrightarrow{AB} \right|=\left| \overrightarrow{C\text{D}} \right|\Leftrightarrow AB=CD\Rightarrow $$Tập hợp điểm $$D$$ là đường tròn tâm $$C$$ bán kính $$AB$$ $$\Rightarrow $$ Có vô số điểm $$D$$ thỏa mãn. Chọn đáp án D.
Câu 15.
Cho $$\overrightarrow{AB}$$ ≠ $$\vec{0}$$ và một điểm C, có bao nhiêu điểm D thỏa mãn. $$\overrightarrow{AB}=\overrightarrow{CD}$$
[A]. $$0. $$
[B]. $$1. $$
[C]. $$2. $$
[D]. Vô số.
HD Với $$A,B,C$$ cố định thì có duy nhất $$1$$ điểm $$D$$ để $$\overrightarrow{AB}=\overrightarrow{CD}$$ Chọn đáp án B.
Câu 16.
Điều kiện nào là điều kiện cần và đủ để $$\overrightarrow{AB}=\overrightarrow{CD}$$.
[A]. A. ABCD là hình bình hành.
[B]. ABDC là hình bình hành.
[C]. C. AD và BC có cùng trung điểm
[D]. AB = CD và AB // CD
HD Chọn đáp án B.
Câu 17.
Cho 2 điểm $$A$$ và $$B$$. Nếu \[\overrightarrow{AB}=\overrightarrow{BA}\] thì
[A]. \[\overrightarrow{AB}\] không cùng phương \[\overrightarrow{BA}. \]
[B]. \[\overrightarrow{AB}=\overrightarrow{0}. \]
[C]. \[AB>0. \]
[D]. $$A\ne B. $$
HD \[\overrightarrow{AB}=\overrightarrow{BA}\Rightarrow A\equiv B\Leftrightarrow \overrightarrow{AB}=\vec{0}\] Chọn đáp án B.
Câu 18.
Cho 3 điểm $$A,B,C$$ phân biệt, thẳng hàng theo thứ tự đó. Tìm mệnh đề sai.
[A]. \[\overrightarrow{AC}\] cùng hướng \[\overrightarrow{BC}. \]
[B]. \[\overrightarrow{AB}\] cùng phương \[\overrightarrow{BC}. \]
[C]. \[\overrightarrow{AB}\] ngược hướng \[\overrightarrow{CB}. \]
[D]. \[\overrightarrow{AC}\] ngược hướng \[\overrightarrow{AB}. \]
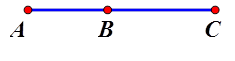
HD Chọn đáp án D.
Câu 19.
Cho hình thoi \[ABCD\] tâm O. Gọi I, J, K lần lượt là trung điểm BC, CD, AD. Tìm mệnh đề sai.
[A]. Có 2 vectơ bằng vectơ $$\overrightarrow{IJ}. $$
[B]. Có 5 vectơ có độ dài bằng vectơ $$\overrightarrow{BO}. $$
[C]. Có 3 vectơ bằng vectơ $$\overrightarrow{BI}. $$
[D]. Có 4 vectơ bằng vectơ $$\overrightarrow{AB}. $$
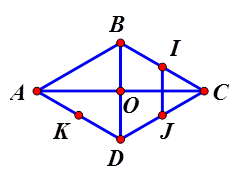
Có 2 vectơ bằng vectơ $$\overrightarrow{IJ}$$là. $$\overrightarrow{BO},\overrightarrow{OD}$$
Có 5 vectơ có độ dài bằng vectơ $$\overrightarrow{BO}$$là. $$\overrightarrow{IJ},\overrightarrow{JI},\overrightarrow{OD},\overrightarrow{DO},\overrightarrow{OB}$$
Có 3 vectơ bằng vectơ $$\overrightarrow{BI}$$ là. $$\overrightarrow{IC},\overrightarrow{AK},\overrightarrow{KD}. $$
Có 2 vectơ bằng vectơ $$\overrightarrow{AB}$$là \[\overrightarrow {DC} ,\overrightarrow {KI} \]
Chọn đáp án D.
Câu 20.
Cho $$\Delta ABC$$ có trực tâm H, nội tiếp trong (O). Gọi M là trung điểm của BC. Gọi A’, B’ lần lượt là điểm đối xứng của A, B qua O. Tìm mệnh đề sai.
[A]. $$\overrightarrow{AB}=\overrightarrow{B’A’}. $$
[B]. $$\overrightarrow{AH}=\overrightarrow{B’C}. $$
[C]. $$\overrightarrow{BH}=\overrightarrow{A’C}. $$
[D]. $$\overrightarrow{MH}=\overrightarrow{MA’}. $$
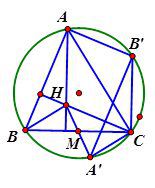
HD Ta có. $$BH\bot AC$$ mà $$\widehat{A’CA}={{90}^{0}}$$ (góc nội tiếp chắn nửa đường tròn) $$\Rightarrow A’C\bot AC\Rightarrow BH//A’C. $$ Chứng min tương tự ta có. $$CH//A’B\Rightarrow A’CHB$$ là hình bình hành. $$\Rightarrow M$$ là trung điểm của $$A’H\Rightarrow \overrightarrow{MA’}=\overrightarrow{MH}$$ Chọn đáp án D.