Dấu của tam thức bậc hai, trắc nghiệm toán 10
Câu 1.
Tam thức bậc hai \[f\left( x \right)=\sqrt{3}{{x}^{2}}+\left( 1+\sqrt{3} \right)x+1\] nhận giá trị âm khi và chỉ khi
[A]. \[x\in \left( -1;-\dfrac{1}{\sqrt{3}} \right). \]
[B]. \[\left( -\dfrac{1}{\sqrt{3}};+\infty
\right). \]
[C]. \[\left( -\infty ;-1 \right). \]
[D]. \[\left( -1;+\infty
\right). \]
\[f\left( x \right)=\sqrt{3}{{x}^{2}}+\left( 1+\sqrt{3} \right)x+1=0\Leftrightarrow \left[ \begin{array}{l}
x=-1 \\
x=-\dfrac{1}{\sqrt{3}}
\end{array} \right. \]
Trục xét dấu:

$\Rightarrow f\left( x \right)<0\Leftrightarrow -1<x<-\dfrac{1}{\sqrt{3}}. $ Chọn đáp án A.
Câu 2.
Tìm điều kiện của $m$để phương trình $(1+m){{x}^{2}}-2mx+2m=0$có hai nghiệm phân biệt:
[A]. $m\in \left( -2;1 \right). $
[B]. $m\in \left[ -2;1 \right]. $
[C]. $m\in \left( -\infty ;-2 \right)\cup \left( 1;+\infty
\right). $
[D]. $m\in \left( -2;1 \right)\backslash \left\{ -1 \right\}. $
Phương trình có hai nghiệm phân biệt
$\Leftrightarrow \left\{ \begin{array}{l}
1+m\ne 0 \\
\Delta ‘={{m}^{2}}-2m\left( 1+m \right)>0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m\ne -1 \\
-{{m}^{2}}-2m>0
\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}
m\ne -1 \\
-2<m<0
\end{array} \right.. $ Chọn đáp án D.
Câu 3.
Tam thức bậc hai \[f\left( x \right)=-{{x}^{2}}+5x-6\] nhận giá trị dương khi và chỉ khi
[A]. \[x\in \left( -\infty ;2 \right). \]
[B]. \[\left( 3;+\infty
\right). \]
[C]. \[x\in \left( 2;+\infty
\right). \]
[D]. \[x\in \left( 2;3 \right). \]
\[f\left( x \right)=-{{x}^{2}}+5x-6=0\Leftrightarrow \left[ \begin{array}{l}
x=2 \\
x=3
\end{array} \right. \]
Trục xét dấu:

$\Rightarrow f\left( x \right)>0\Leftrightarrow 2<x<3. $ Chọn đáp án D.
Câu 4.
Biểu thức \[M\left( x \right)=\dfrac{2{{x}^{2}}+3x-5}{{{x}^{2}}-x-2}\] luôn không âm trên khoảng
[A]. \[\left( -\dfrac{5}{2};-1 \right)\]và \[\left( 1;2 \right). \]
[B]. \[\left[ -\dfrac{5}{2};-1 \right)\]và \[\left( 2;+\infty
\right). \]
[C]. \[\left( -\infty ;\dfrac{5}{2} \right]\] và \[\left[ 1,2 \right). \]
[D]. \[\left( -\infty ;\dfrac{5}{2} \right]\]; \[\left( -1;1 \right]\] và \[\left( 2;+\infty
\right). \]
Xét: $2{{x}^{2}}+3x-5=0\Leftrightarrow \left[ \begin{array}{l}
x=1 \\
x=-\dfrac{5}{2}
\end{array} \right. ;{{x}^{2}}-x-2=0\Leftrightarrow \left[ \begin{array}{l}
x=-1 \\
x=2
\end{array} \right. $
Trục xét dấu:

$\Rightarrow M\left( x \right)\ge 0\Leftrightarrow \left[ \begin{array}{l}
x\le -\dfrac{5}{2} \\
-1<x\le 1 \\
x>2
\end{array} \right.. $ Chọn đáp án D.
Câu 5.
Có bao nhiêu giá trị $m$ nguyên để phương trình $(3-m){{x}^{2}}-2(m+3)x+m+2=0$ vô nghiệm?
[A]. $0. $
[B]. $2. $
[C]. $3. $
[D]. $1. $
Với $m=3\Rightarrow pt\Leftrightarrow x=\dfrac{5}{12}\Rightarrow m=3$ Loại.
Với $m\ne 3. $ Phương trình vô nghiệm $\Leftrightarrow \Delta ‘={{\left( m+3 \right)}^{2}}-\left( 3-m \right)\left( m+2 \right)<0$
$\Leftrightarrow 2{{m}^{2}}+5m+3<0\Leftrightarrow -\dfrac{3}{2}<m<-1\xrightarrow{m\in \mathbb{Z}}$ Không có giá trị $m$ nguyên thỏa mãn.
Chọn đáp án A.
Câu 6.
Số giá trị nguyên của $m$để bất phương trình $3{{x}^{2}}+2(m-1)x+m+5\ge 0$nghiệm đúng với mọi $x$ là:
[A]. $0. $
[B]. $3. $
[C]. $7. $
[D]. $10. $
$3{{x}^{2}}+2(m-1)x+m+5\ge 0,\forall x\in \mathbb{R}$
$\Leftrightarrow \Delta ‘={{\left( m-1 \right)}^{2}}-3\left( m+5 \right)\le 0$
$\Leftrightarrow {{m}^{2}}-5m-14\le 0\Leftrightarrow -2\le m\le 7\xrightarrow{m\in \mathbb{Z}}m=\left\{ -2;-1;0;1;2;3;4;5;6;7 \right\}$
Chọn đáp án D.
Câu 7.
Các giá trị $m$ làm cho biểu thức \[{{x}^{2}}+4x+m5\] luôn luôn dương là:
[A]. \[m<9. \]
[B]. \[m>9. \]
[C]. \[m\ge 9. \]
[D]. \[m\in \varnothing . \]
\[{{x}^{2}}+4x+m5>0,\forall x\in \mathbb{R}\Leftrightarrow \Delta ‘<0\Leftrightarrow 4-m+5<0\Leftrightarrow m>9. \] Chọn đáp án B.
Câu 8.
Số nghiệm nguyên của bất phương trình ${{x}^{2}}-7x+10<0$là:
[A]. $0. $
[B]. $1. $
[C]. $2. $
[D]. \[3. \]
Xét: ${{x}^{2}}-7x+10=0\Leftrightarrow \left[ \begin{array}{l}
x=2 \\
x=5
\end{array} \right. $
Trục xét dấu:

$\Rightarrow {{x}^{2}}-7x+10<0\Leftrightarrow 2<x<5\xrightarrow{x\in \mathbb{Z}}x=\left\{ 3;4 \right\}. $ Chọn đáp án C.
Câu 9.
Cho tam thức bậc hai được liệt kê ở một trong bốn phương án A, B, C, D có bảng xét dấu như hình bên dưới. Hỏi đó là tam thức bậc hai nào?
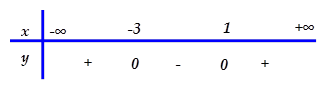
[A]. $y={{x}^{2}}+2x-3. $
[B]. $y=-{{x}^{2}}-2x+3. $
[C]. $y={{x}^{2}}-4x+3. $
[D]. $y=-{{x}^{2}}+4x-3. $
Áp dụng “trong trái, ngoài cùng” $\Rightarrow a>0$ $\Rightarrow $ Loại B, D.
Tam thức có nghiệm $x=-3;x=1\Rightarrow $ Chọn đáp án A.
Câu 10.
Bảng xét dấu nào sau đây là của tam thức: $f\left( x \right)={{x}^{2}}+6x+9$
[A]. 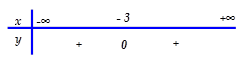
[B]. 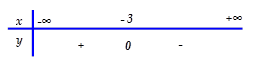
[C]. 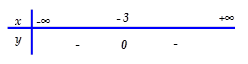
[D]. 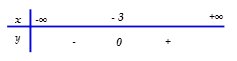
$f\left( x \right)={{x}^{2}}+6x+9=0\Leftrightarrow x=-3$ $\Rightarrow $ Phương trình có nghiệm kép.
$\Rightarrow f\left( x \right)\ge 0,\forall x\in \mathbb{R}. $ Chọn đáp án A.
Câu 11.
Tam thức bậc hai \[f\left( x \right)=-0,3{{x}^{2}}+x-1,5\] nhận giá trị âm khi và chỉ khi
[A]. \[x\in \left( -1;3 \right). \]
[B]. \[x\in \left( -\infty ;3 \right). \]
[C]. \[x\in \mathbb{R}. \]
[D]. \[\left( -1;+\infty
\right). \]
\[f\left( x \right)=-0,3{{x}^{2}}+x-1,5=0\Leftrightarrow \] Vô nghiệm.
$a=-0,3<0\Rightarrow f\left( x \right)<0,\forall x\in \mathbb{R}. $ Chọn đáp án C.
Câu 12.
Biểu thức $f\left( x \right)=\dfrac{{{x}^{2}}+9}{\left( {{x}^{2}}-1 \right)\left( 4-{{x}^{2}} \right)}$ không dương khi
[A]. $x\in \left( -\infty ;-2 \right)\cup \left( -1;1 \right)\cup \left( 2;+\infty
\right). $
[B]. $x\in \left( -2;-1 \right)\cup \left( 1;2 \right). $
[C]. $x\in \left( -\infty ;-2 \right]\cup \left[ -1;1 \right]\cup \left[ 2;+\infty
\right). $
[D]. $x\in \left[ -2;-1 \right]\cup \left[ 1;2 \right]. $
${{x}^{2}}+9=0\Leftrightarrow $ Vô nghiệm; ${{x}^{2}}-1=0\Leftrightarrow x=\pm 1;4-{{x}^{2}}=0\Leftrightarrow x=\pm 2. $
Trục xét dấu:

$f\left( x \right)\le 0\Leftrightarrow x\in \left( -\infty ;-2 \right)\cup \left( -1;1 \right)\cup \left( 2;+\infty
\right). $ Chọn đáp án A.
Câu 13.
Tìm tập xác định của hàm số $y=\sqrt{\dfrac{{{x}^{2}}+3}{{{x}^{2}}+5x+4}}$ là:
[A]. $D=\mathbb{R}. $
[B]. $D=\mathbb{R}\backslash \left[ -4;-1 \right]. $
[C]. $D=\mathbb{R}\backslash \left( -4;-1 \right). $
[D]. $\text{D}=\left[ -4;-1 \right]. $
Điều kiện xác định của hàm số: $\left\{ \begin{array}{l}
\dfrac{{{x}^{2}}+3}{{{x}^{2}}+5x+4}\ge 0 \\
{{x}^{2}}+5x+4\ne 0
\end{array} \right. \Leftrightarrow {{x}^{2}}+5x+4>0\Leftrightarrow \left[ \begin{array}{l}
x>-1 \\
x<-4
\end{array} \right.. $ Chọn đáp án B.
Câu 14.
Tìm tất cả các giá trị thực của tham số \[m\] sao cho phương trình \[{{x}^{2}}+\left( m+1 \right)x+m-\dfrac{1}{3}=0\] có nghiệm.
[A]. \[m\in \mathbb{R}. \]
[B]. \[m>1. \]
[C]. \[-\dfrac{3}{4}<m<1. \]
[D]. \[m>-\dfrac{3}{4}. \]
Phương trình có nghiệm $\Leftrightarrow \Delta ={{\left( m+1 \right)}^{2}}-4\left( m-\dfrac{1}{3} \right)\ge 0$
$\Leftrightarrow {{m}^{2}}-2m+\dfrac{7}{3}\ge 0\Leftrightarrow \forall m. $ Chọn đáp án A.
Câu 15.
Biểu thức $\left( 3{{x}^{2}}-10x+3 \right)\left( 4x-5 \right)$ âm khi
[A]. $x\in \left( -\infty ;\dfrac{5}{4} \right). $
[B]. $x\in \left( -\infty ;\dfrac{1}{3} \right)\cup \left( \dfrac{5}{4};3 \right). $
[C]. $x\in \left( \dfrac{1}{3};\dfrac{5}{4} \right)\cup \left( 3;+\infty
\right). $
[D]. $x\in \left( \dfrac{1}{3};3 \right). $
Xét $3{{x}^{2}}-10x+3=0\Leftrightarrow \left[ \begin{array}{l}
x=3 \\
x=\dfrac{1}{3}
\end{array} \right. ;4x-5=0\Leftrightarrow x=\dfrac{5}{4}$
Trục xét dấu:
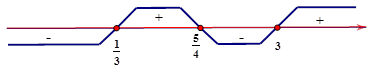
$\Rightarrow f\left( x \right)<0\Leftrightarrow \left[ \begin{array}{l}
x<\dfrac{1}{3} \\
\dfrac{5}{4}<x<3
\end{array} \right.. $ Chọn đáp án B.
Câu 16.
Biểu thức $f\left( x \right)=\dfrac{\left( 3{{x}^{2}}-x \right)\left( 4-{{x}^{2}} \right)}{{{x}^{2}}+2x+3}$ dương khi
[A]. $x\in \left( -\infty ;-2 \right)\cup \left( 0;\dfrac{1}{3} \right)\cup \left( 2;+\infty
\right). $
[B]. $x\in \left( -\infty ;0 \right)\cup \left( \dfrac{1}{3};+\infty
\right). $
[C]. $x\in \left( -2;0 \right)\cup \left( \dfrac{1}{3};2 \right). $
[D]. $x\in \left( -2;2 \right). $
$3{{x}^{2}}-x=0\Leftrightarrow \left[ \begin{array}{l}
x=0 \\
x=\dfrac{1}{3}
\end{array} \right. ;4-{{x}^{2}}=0\Leftrightarrow x=\pm 2;{{x}^{2}}+2x+3=0\Leftrightarrow $ Vô nghiệm.
Trục xét dấu:

$f\left( x \right)>0\Leftrightarrow \left[ \begin{array}{l}
-2<x<0 \\
\dfrac{1}{3}<x<2
\end{array} \right.. $ Chọn đáp án C.
Câu 17.
Tìm tất cả các giá trị của $m$để phương trình ${{x}^{2}}+\left( m+3 \right)x+m+2=0$ có nghiệm:
[A]. $m\in \varnothing . $
[B]. $m\in \left( -1;1 \right). $
[C]. $m\in \left( 0;1 \right). $
[D]. $m\in \mathbb{R}. $
Phương trình có nghiệm $\Leftrightarrow \Delta ={{\left( m+3 \right)}^{2}}-4\left( m+2 \right)={{m}^{2}}+2m+1\ge 0,\forall m. $ Chọn đáp án D.
Câu 18.
Tam thức bậc hai \[f\left( x \right)={{x}^{2}}+\left( \sqrt{5}-1 \right)x-\sqrt{5}\] nhận giá trị dương khi và chỉ khi
[A]. \[x\in \left( -\sqrt{5};1 \right). \]
[B]. \[x\in \left( -\sqrt{5};+\infty
\right). \]
[C]. \[x\in \left( -\infty ;-\sqrt{5} \right)\cup \left( 1;+\infty
\right). \]
[D]. \[x\in \left( -\infty ;1 \right). \]
\[f\left( x \right)={{x}^{2}}+\left( \sqrt{5}-1 \right)x-\sqrt{5}=0\Leftrightarrow \left[ \begin{array}{l}
x=1 \\
x=-\sqrt{5}
\end{array} \right. \]
Trục xét dấu:

$f\left( x \right)>0\Leftrightarrow \left[ \begin{array}{l}
x<-\sqrt{5} \\
x>1
\end{array} \right.. $ Chọn đáp án C.
Câu 19.
Biểu thức $f\left( x \right)=-{{x}^{2}}+3x-2$ không âm khi
[A]. $x\in \left( -\infty ;1 \right)\cup \left( 2;+\infty
\right). $
[B]. $x\in \left[ 1;2 \right]. $
[C]. $x\in \left( -\infty ;1 \right]\cup \left[ 2;+\infty
\right). $
[D]. $x\in \left( 1;2 \right). $
$f\left( x \right)=-{{x}^{2}}+3x-2=0\Leftrightarrow \left[ \begin{array}{l}
x=1 \\
x=2
\end{array} \right. $
Trục xét dấu:

$f\left( x \right)\ge 0\Leftrightarrow 1\le x\le 2. $ Chọn đáp án B.
Câu 20.
Tìm điều kiện của $m$để phương trình $(m-2){{x}^{2}}-4mx+2m-6=0$vô nghiệm:
[A]. $m\in \left( -6;1 \right). $
[B]. $m\in \left( -\infty ;-6 \right)\cup \left( 1;+\infty
\right). $
[C]. $m\in \left( -6;1 \right)\backslash \left\{ 0 \right\}. $
[D]. $m\in \mathbb{R}\backslash \left\{ 2 \right\}. $
Với $m=2\Rightarrow pt\Leftrightarrow x=-\dfrac{1}{4}\Rightarrow m=2$ Loại
Với $m\ne 2. $ Phương trình vô nghiệm $\Leftrightarrow \Delta ‘=4{{m}^{2}}-\left( 2m-6 \right)\left( m-2 \right)<0$
$\Leftrightarrow 2{{m}^{2}}+10m-12<0\Leftrightarrow -6<m<1. $ Chọn đáp án A.