Bất phương trình và hệ bất phương trình bậc nhất hai ẩn, trắc nghiệm toán 10
Câu 1.
Cặp số \[\left( 1;-1 \right)\] là nghiệm của bất phương trình nào sau đây ?
[A]. \[x+y-3>0. \]
[B]. \[-x-y<0. \]
[C]. \[x+3y+1<0. \]
[D]. \[-x-3y-1<0. \]
Thay $\left\{ \begin{array}{l}
x=1 \\
y=-1
\end{array} \right. $ vào các bất phương trình ta chọn đáp án C.
Câu 2.
Cặp số nào là nghiệm của bất phương trình $-2x+3y-3>0?$
[A]. \[\left( 4;-4 \right). \]
[B]. \[\left( 2;1 \right). \]
[C]. \[\left( -1;-2 \right). \]
[D]. \[\left( 4;4 \right). \]
Thử các đáp án ta chọn đáp án D.
Câu 3.
Cặp số nào không là nghiệm của bất phương trình $5x-2y+2\le 0$
[A]. \[\left( 0;1 \right). \]
[B]. \[\left( 1;3 \right). \]
[C]. \[\left( -1;1 \right). \]
[D]. \[\left( -1;0 \right). \]
Thử các đáp án ta chọn đáp án B.
Câu 4.
Trong các cặp số sau, cặp số nào là nghiệm của bất phương trình $3x-2y+1>0$
[A]. $\left( 0;0 \right). $
[B]. $\left( -1;0 \right). $
[C]. $\left( -2;-1 \right). $
[D]. $\left( 0;1 \right). $
Thử các đáp án ta chọn đáp án A.
Câu 5.
Tập nghiệm của bất phương trình $x-2y+5<0$ là:
[A]. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng $y=\dfrac{1}{2}x+\dfrac{5}{2}$ (không bao gồm đường thẳng).
[B]. Nửa mặt phẳng
chứa gốc tọa độ, bờ là đường thẳng $y=\dfrac{1}{2}x+\dfrac{5}{2}$ (không bao gồm đường thẳng).
[C]. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng $y=\dfrac{1}{2}x+\dfrac{5}{2}$ (bao gồm đường thẳng).
[D]. Nửa mặt phẳng
chứa gốc tọa độ, bờ là đường thẳng $y=\dfrac{1}{2}x+\dfrac{5}{2}$ (không bao gồm đường thẳng).
Xét đường thẳng $x-2y+5=0\Leftrightarrow y=\dfrac{x}{2}+\dfrac{5}{2}. $
Thay tọa độ điểm $O\left( 0;0 \right)$ vào bất phương trình ta được: $5<0$ $\Rightarrow $ không thỏa mãn.
Chọn đáp án A.
Câu 6.
Biểu diễn hình học tập nghiệm của bất phương trình $-4x+y<2$ là
[A]. Nửa mặt phẳng bờ là đường thẳng $\Delta : -4x+y-2=0$ và chứa điểm $O(0;0)$ – không kể đường thẳng $\Delta $.
[B]. Nửa mặt phẳng bờ là đường thẳng $\Delta : -4x+y-2=0$.
[C]. Nửa mặt phẳng bờ là đường thẳng $\Delta : -4x+y-2=0$ và không chứa điểm $O(0;0)$ – không kể đường thẳng $\Delta $.
[D]. Nửa mặt phẳng bờ là đường thẳng $\Delta : -4x+y-2=0$ và chứa điểm $O(0;0)$ – kể cả đường thẳng $\Delta $.
Xét đường thẳng $-4x+y=2\Leftrightarrow y=4x+2. $
Thay tọa độ điểm $O\left( 0;0 \right)$ vào bất phương trình ta được: $0<2$ (thỏa mãn).
Chọn đáp án A.
Câu 7.
Chọn câu
đúng. Miền nghiệm của bất phương trình: \[3x+2\left( y+3 \right)>4\left( x+1 \right)-y+3\] là phần mặt
phẳng chứa điểm:
[A]. \[\left( 3;0 \right). \]
[B]. \[\left( 3;1 \right). \]
[C]. \[\left( 1;2 \right). \]
[D]. \[\left( 0;0 \right). \]
\[3x+2\left( y+3 \right)>4\left( x+1 \right)-y+3\Leftrightarrow x-3y+1<0\]
Thay tọa độ các điểm vào bất phương trình ta chọn đáp án C.
Câu 8.
Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình
\[\left\{ \begin{array}{l}
x+3y-2\ge 0 \\
2x+y+1\le 0
\end{array} \right. \]:
[A]. \[\left( 0;1 \right). \]
[B]. \[\left( -1;1 \right). \]
[C]. \[\left( 1;3 \right). \]
[D]. \[\left( -1;0 \right). \]
Lần lượt thay tọa độ các điểm vào hệ ta chọn đáp án B.
Câu 9.
Trong các điểm sau , điểm nào thuộc miền nghiệm của hệ bất phương trình
\[\left\{ \begin{array}{l}
x-y-2\le 0 \\
x+2y+1>0
\end{array} \right. \]:
[A]. \[\left( 0;-1 \right). \]
[B]. \[\left( -1;-2 \right). \]
[C]. \[\left( 11;3 \right). \]
[D]. \[\left( 1;0 \right). \]
Lần lượt thay tọa độ các điểm vào hệ ta chọn đáp án D.
Câu 10.
Hệ bất phương trình sau có bao nhiêu cặp \[\left( x,y \right)\] nghiệm và\[x\],\[y\] đều nguyên\[\left\{ \begin{array}{l}
x+y<5 \\
x>1 \\
y>-1
\end{array} \right. \]
[A]. $4. $
[B]. $6. $
[C]. $5. $
[D]. Vô số.
Ta có: $x+y<5\Leftrightarrow x<5-y$
Mà $x>1\Leftrightarrow 5-y>1\Leftrightarrow y<4. $
Ta có: $-1<y<4\Rightarrow y=\left\{ 0;1;2;3 \right\}$
Với $y=0\Rightarrow 1<x<5\Rightarrow x=\left\{ 2;3;4 \right\}\Rightarrow $ Nghiệm nguyên của hệ $\left( 2;0 \right),\left( 3;0 \right),\left( 4;0 \right)$
Với $y=1\Rightarrow 1<x<4\Rightarrow x=\left\{ 2;3 \right\}\Rightarrow $ Nghiệm nguyên của hệ $\left( 2;1 \right);\left( 3;1 \right)$
Với $y=2\Rightarrow 1<x<3\Rightarrow x=2\Rightarrow $ Nghiệm nguyên của hệ $\left( 2;2 \right)$
Với $y=4\Rightarrow 1<x<1\Leftrightarrow $ không có $x$ nguyên.
Vậy, hệ có $6$ nghiệm mà $x,y$ đều nguyên. Chọn đáp án B.
Câu 11.
Hệ bất phương trình sau có bao nhiêu cặp \[\left( x,y \right)\] nghiệm và\[x\],\[y\] đều nguyên dương \[\left\{ \begin{array}{l}
x+y<5 \\
x+2y>5
\end{array} \right. \]
[A]. $3. $
[B]. $2. $
[C]. $6. $
[D]. $4. $
$x+y<5\Leftrightarrow x<5-y$ Mà $x>0\Rightarrow 5-y>0\Leftrightarrow y<5$
$\xrightarrow{y\in \mathbb{Z}*}y=\left\{ 1;2;3;4 \right\}$
Với $y=1\Rightarrow \left\{ \begin{array}{l}
x<4 \\
x>3
\end{array} \right. \Rightarrow $ Không có giá trị $x$ nguyên dương thỏa mãn.
Với $y=2\Rightarrow \left\{ \begin{array}{l}
x<3 \\
x>1
\end{array} \right. \xrightarrow{x\in \mathbb{Z}*}x=2\Rightarrow $ Nghiệm nguyên dương của hệ $\left( 2;2 \right)$
Với $y=3\Rightarrow \left\{ \begin{array}{l}
x<2 \\
x>-1
\end{array} \right. \xrightarrow{x\in \mathbb{Z}*}x=1\Rightarrow $ Nghiệm nguyên dương của hệ $\left( 1;3 \right)$
Với $y=4\Rightarrow \left\{ \begin{array}{l}
x<1 \\
x>-3
\end{array} \right. \xrightarrow{x\in \mathbb{Z}*}$ không có $x$ thỏa mãn.
Chọn đáp án B.
Câu 12.
Hình sau đây biểu diễn miền nghiệm cho bất phương trình nào? (Miền nghiệm là phần tô màu)
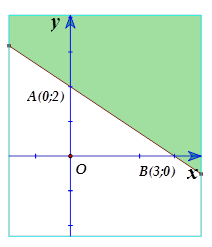
[A]. \[x+3y-6>0. \]
[B]. \[2x+y-2<0. \]
[C]. \[2x+3y-6>0. \]
[D]. \[2x+3y-6<0. \]
Đường “ranh giới” đi qua hai điểm $A\left( 0;2 \right);B\left( 3;0 \right)\Rightarrow $ Loại A, B.
Gốc tọa độ $O\left( 0;0 \right)$ không thuộc miền nghiệm của bất phương trình. Chọn đáp án C.
Câu 13.
Hình sau đây biểu diễn cho hệ bất phương trình nào? (Miền nghiệm là phần tô màu)
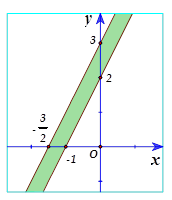
[A]. $\left\{ \begin{array}{l}
x-y\le 3 \\
x+2y\ge 5x+4
\end{array} \right.. $
[B]. $\left\{ \begin{array}{l}
2x-y\le 3 \\
2x+4y\ge 10x+8
\end{array} \right.. $
[C]. $\left\{ \begin{array}{l}
2x-y\le 3 \\
2x-y+2\le 0
\end{array} \right.. $
[D]. $\left\{ \begin{array}{l}
-2x+y\le 3 \\
2x+4y\ge 10x+8
\end{array} \right.. $
Điểm $O\left( 0;0 \right)$ không thuộc miền nghiệm của hệ. Thử các đáp án ta chọn đáp án D.
Chọn câu sai.
Câu 14.
Miền nghiệm của hệ bất phương trình$\left\{ \begin{matrix}
2x+3y-1>0
\\
5x-y+4<0
\\
\end{matrix} \right. $ là phần mặt phẳng không chứa điểm:
[A]. \[\left( -1;4 \right). \]
[B]. \[\left( 0;0 \right). \]
[C]. \[\left( -2;4 \right). \]
[D]. \[\left( -3;4 \right). \]
Thử từng đáp án. Chọn đáp án B.
Câu 15.
[A]. \[\left( 0;0 \right). \]
[B]. \[\left( 1;0 \right). \]
[C]. \[\left( 0;-2 \right). \]
[D]. \[\left( 0;2 \right). \]
Thử từng đáp án. Chọn đáp án C.
Câu 16.
Giá trị nhỏ nhất của biết thức \[F(x;y)=\text{ }y-x\] trên miền xác định bởi hệ: $\left\{ \begin{matrix}
y-2x\le 2
\\
2y-x\ge 4
\\
x+y\le 5
\\
\end{matrix} \right. $
là:
[A]. \[min\text{ }F=1\text{ }\] khi \[x\text{ }=2,\text{ }y=3. \]
[B]. \[min\text{ }F=\text{ }2\text{ }\] khi \[x=0,\text{ }y=2. \]
[C]. \[min\text{ }F=3\] khi \[x=1,\text{ }y=4. \]
[D]. Một kết quả khác.
Ta có: $\left\{ \begin{matrix}
y-2x\le 2
\\
2y-x\ge 4
\\
x+y\le 5
\\
\end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix}
y-2x-2\le 0
\\
2y-x-4\ge 0
\\
x+y-5\le 0
\\
\end{matrix} \right. \,\,\,\,\,(*)$
Trước hết, ta vẽ ba đường thẳng:
${{d}_{1}}: y-2x-2=0,{{d}_{2}}: 2y-x-4=0,{{d}_{3}}: x+y-5=0. $
Tọa độ giao điểm của ${{d}_{1}},{{d}_{2}}$ là nghiệm của hệ phương trình:
$\left\{ \begin{array}{l}
y-2x-2=0 \\
2y-x-4=0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=0 \\
y=2
\end{array} \right. \Rightarrow A\left( 0;2 \right). $
Tọa độ giao điểm của ${{d}_{2}},{{d}_{3}}$ là nghiệm của hệ phương trình:
$\left\{ \begin{array}{l}
2y-x-4=0 \\
x+y-5=0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=2 \\
y=3
\end{array} \right. \Rightarrow B\left( 2;3 \right). $
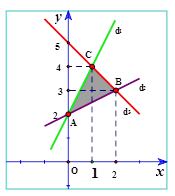
Tọa độ giao điểm của ${{d}_{1}},{{d}_{3}}$ là nghiệm của hệ phương trình:
$\left\{ \begin{array}{l}
y-2x-2=0 \\
x+y-5=0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=1 \\
y=4
\end{array} \right. \Rightarrow C\left( 1;4 \right). $
Khi đó, miền nghiệm của hệ bất phương trình $\left( * \right)$ là phần mặt phẳng (tam giác $ABC)$ (hình vẽ)
Giá trị nhỏ nhất của biết thức \[F(x;y)=\text{ }yx\] sẽ đạt được tại một trong các điểm $A,B,C. $
Ta có: $F\left( 0;2 \right)=2,F\left( 2;3 \right)=1,F\left( 1;4 \right)=3. $
$\Rightarrow $ \[min\text{ }F=1\text{ }\] khi \[x\text{ }=2,\text{ }y=3. \] Chọn đáp án A.
Câu 17.
Biểu thức \[F=y-x\] đạt giá trị nhỏ nhất với điều kiện: \[\left\{ \begin{matrix}
2x-y\ge 2
\\
x-2y\le 2
\\
x+y\le 5
\\
x\ge 0
\\
\end{matrix} \right. \]tại điểm \[M\] có toạ độ là:
[A]. \[\left( 4;1 \right). \]
[B]. \[\left( \dfrac{8}{3};-\dfrac{7}{3} \right). \]
[C]. \[\left( \dfrac{2}{3};-\dfrac{2}{3} \right). \]
[D]. \[\left( 5;0 \right). \]
Giải các hệ phương trình \[\left\{ \begin{array}{l}
2x-y=2 \\
x-2y=2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=\dfrac{2}{3} \\
y=-\dfrac{2}{3}
\end{array} \right. \] ; \[\left\{ \begin{array}{l}
2x-y=2 \\
x+y=5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=\dfrac{7}{3} \\
y=\dfrac{8}{3}
\end{array} \right. \] ; \[\left\{ \begin{array}{l}
x-2y=2 \\
x+y=5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x=4 \\
y=1
\end{array} \right. \] nên chỉ có đáp án A và C là đỉnh của đa giác miền nghiệm.
So sánh \[F=y-x\] ứng với tọa độ ở đáp án A và C, ta được đáp án \[\left( 4;1 \right)\]. Chọn đáp án A.
Câu 18.
Cho \[x,y\] thoả mãn hệ \[\left\{ \begin{array}{l}
x+2y-100\le 0 \\
2x\,\,+\,y-80\,\,\le 0 \\
x\ge 0 \\
y\ge 0
\end{array} \right. \] . Giá trị lớn nhất của \[L\left( x;y \right)=40000x+30000y\]
bằng?
[A]. $\underset{{}}{\mathop{Max}}\,L=2000000$ khi $x=20,y=40. $
[B]. $\underset{{}}{\mathop{Max}}\,L=2400000$ khi $x=30,y=40. $
[C]. $\underset{{}}{\mathop{Max}}\,L=1800000$ khi $x=30,y=20. $
[D]. Một giá trị khác.
Trong mặt phẳng tọa độ $Oxy,$vẽ các đường thẳng $\left( d \right): x+2y-100=0,\,\,\left( d’ \right): 2x+y-80=0$
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác $OABC$) tô màu trên hình vẽ
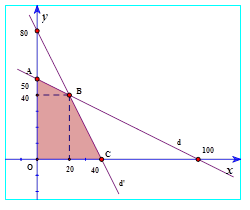
Giá trị lớn nhất của \[L\left( x;y \right)=40000x+30000y\] đạt tại một trong các điểm \[\left( 0;0 \right),\,\,\left( 40;0 \right),\,\,\left( 0;50 \right),\,\,\left( 20;40 \right)\]. Ta có \[L\left( 0;0 \right)=0,\,\,L\left( 40;0 \right)=1600000,\] \[L\left( 0;50 \right)=1500000,\,\,L\left( 20;40 \right)=2000000\] suy ra giá trị lớn nhất của \[L\left( x;y \right)\] là \[2000000\] khi $\left( x;y \right)=\left( 20;40 \right)$. Chọn đáp án A.
Câu 19.
Giá trị lớn nhất của biết thức \[F\left( x;y \right)=\text{ }x+2y\] với điều kiện: $\left\{ \begin{matrix}
0\le y\le 4
\\
x\ge 0
\\
x-y-1\le 0
\\
x+2y-10\le 0
\\
\end{matrix} \right. $
là:
[A]. \[6. \]
[B]. \[8. \]
[C]. \[10. \]
[D].
\[12. \]
Trong mặt phẳng tọa độ vẽ các đường thẳng $\left( d \right): x-y-1=0,\,\,\left( d’ \right): x+2y-10=0,\left( \Delta
\right): y=4. $
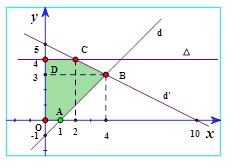
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(ngũ giác $OABCD$) tô màu trên hình vẽ
Giá trị lớn nhất của \[F\left( x;y \right)=\text{ }x+2y\]đạt tại một trong các điểm:
$O\left( 0;0 \right),A\left( 1;0 \right),B\left( 4;3 \right),C\left( 2;4 \right),D\left( 0;4 \right)$
Ta có: $F\left( 0;0 \right)=0,F\left( 1;0 \right)=1,F\left( 4;3 \right)=10,F\left( 2;4 \right)=10,F\left( 0;4 \right)=8. $
$\Rightarrow $ Giá trị lớn nhất của \[F\left( x;y \right)=\text{ }x+2y\]bằng $10. $ Chọn đáp án C.
Câu 20.
Giá trị nhỏ nhất của \[T\left( x,\text{ }y \right)=4x+3y\] với điều kiện: \[\,\,\left\{ \begin{array}{l}
0\le \,\,x\,\,\le \,\,10 \\
0\,\,\le \,\,y\,\,\le \,\,9 \\
2x\,\,+\,\,y\,\,\ge \,\,14 \\
2x\,\,+\,\,5y\,\,\ge \,\,30
\end{array} \right. \]
[A]. \[28. \]
[B]. \[32. \]
[C]. \[12. \]
[D]. \[46. \]
Trong mặt phẳng tọa độ $Oxy,$vẽ các đường thẳng:
$\left( d \right): 2x+y-14=0,\,\,\left( d’ \right): 2x+5y-30=0,$
$\left( \Delta
\right): y=9,\left( \Delta ‘ \right): x=10. $
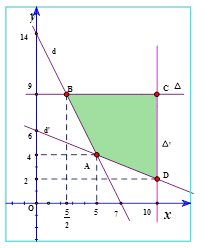
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng (tứ giác $ABCD$) tô màu trên hình vẽ
Giá trị nhỏ nhất của \[T\left( x,\text{ }y \right)=4x+3y\]đạt tại một trong các điểm:
$A\left( 5;4 \right),B\left( \dfrac{5}{2};9 \right),C\left( 10;9 \right),D\left( 10;2 \right)$
Ta có: $T\left( 5;4 \right)=32,T\left( \dfrac{5}{2};9 \right)=37,T\left( 10;9 \right)=67,T\left( 10;2 \right)=46. $
$\Rightarrow $ Giá trị nhỏ nhất của \[T\left( x,\text{ }y \right)=4x+3y\] bằng $32$ tại $x=5,y=4. $ Chọn đáp án B.
Câu 21.
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.
+ Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;
+ Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
[A]. $5$ lít nước cam và $4$ lít nước táo.
[B]. $6$ lít nước cam và $5$ lít nước táo.
[C]. $4$ lít nước cam và $5$ lít nước táo.
[D].
$4$ lít nước cam và $6$ lít nước táo.
Giả sử \[x,\text{ }y\] lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
Suy ra
\[30x+10y\] là số gam đường cần dùng;
\[x+y\] là số lít nước cần dùng;
\[x+4y\] là số gam hương liệu cần dùng.
Theo giả thiết ta có \[\left\{ \begin{array}{l}
x\ge 0 \\
y\ge 0 \\
30x+10y\le 210 \\
x+y\le 9 \\
x+4y\le 24
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x\ge 0 \\
y\ge 0 \\
3x+y\le 21 \\
x+y\le 9 \\
x+4y\le 24
\end{array} \right. \].
$\left( * \right)$
Số điểm thưởng nhận được sẽ là \[P=60x+80y. \]
Trong mặt phẳng tọa độ $Oxy,$vẽ các đường thẳng:
$\left( d \right): 3x+y-21=0,\,\,\left( d’ \right): x+y-9=0,\left( \Delta
\right): x+4y-24=0$
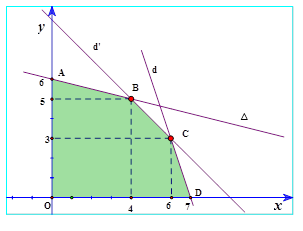
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(ngũ giác $OABCD$) tô màu trên hình vẽ
Xét các đỉnh của miền khép kín tạo ra bởi hệ $\left( * \right)$ là
\[O\left( 0;0 \right),\text{ }A\left( 0;6 \right),\text{ }B\left( 4;5 \right),\text{ }C\left( 6;3 \right)\] và \[D\left( 7;0 \right)\].
Ta thấy \[P\] đạt giá trị lớn nhất tại \[x=4,\text{ }y=5\]. Khi đó \[P=60. 4+80. 5=640. \]
Vậy cần pha chế 4 lít nước cam và 5 lít nước táo để được số điểm cao nhất là $640$.
Chọn đáp án C.
Câu 22.
Một xưởng sản xuất hai loại sản phẩm
+ Mỗi kg sản phẩm loại I cần 2kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;
+ Mỗi kg sản phẩm loại II cần 4kg nguyên liệu và 15giờ, đem lại mức lời 30 nghìn.
Xưởng có 200kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
[A]. $30$kg loại I và $40$ kg loại II.
[B]. $20$kg loại I và $40$ kg loại II.
[C]. $30$kg loại I và $20$ kg loại II.
[D]. $25$kg loại I và $45$ kg loại II.
Gọi \[x,y\,\,(kg)\] lần lượt là số sản phẩm loại I và loại II cần sản xuất. $(x\ge 0,y\ge 0)$
Khi đó, tổng số nguyên liệu sử dụng: $2x+4y\le 200. $
Tổng số giờ làm việc: $30x+15y\le 1200. $
Lợi nhuận tạo thành: $L=40x+30y$ (nghìn)
Thực chất của bài toán này là phải tìm $x\,\,\ge \,\,0$, $y\,\,\ge \,\,0$ thoả mãn hệ $\left\{ \begin{array}{l}
2x\,\,+\,\,4y\,\,\le \,\,200 \\
30x\,\,+\,\,15y\,\,\le \,\,1200
\end{array} \right. $
sao cho $L=40x+30y$đạt giá trị lớn nhất.
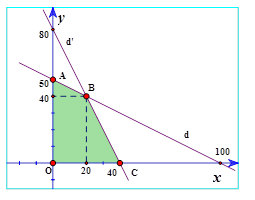
Trong mặt phẳng tọa độ $Oxy,$vẽ các đường thẳng: $\left( d \right): x+2y-100,\,\,\left( d’ \right): 2x+y-80$
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(ngũ giác $OABCD$) tô màu trên hình vẽ
Xét các đỉnh của miền khép kín tạo ra bởi hệ $\left( * \right)$ là
\[O\left( 0;0 \right),\text{ }A\left( 0;50 \right),\text{ }B\left( 20;40 \right),\text{ }C\left( 40;0 \right)\]
Ta có: $L\left( 0;0 \right)=0,L\left( 0;50 \right)=1500,L\left( 20;40 \right)=2000,L\left( 0;40 \right)=1200$
$\Rightarrow $ Giá trị lớn nhất của $L=40x+30y$bằng $2000$ khi $x=20,y=40. $
Chọn đáp án B.
Câu 23.
Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin B và không quá 500 đơn vị vitamin B. Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A. Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.
[A]. $600$ đơn vị Vitamin A, $400$ đơn vị Vitamin $B. $
[B]. $600$ đơn vị Vitamin A, $300$ đơn vị Vitamin $B. $
[C]. $500$ đơn vị Vitamin A, $500$ đơn vị Vitamin $B. $
[D]. $100$ đơn vị Vitamin A, $300$ đơn vị Vitamin $B. $
Gọi $x,y$$(x\ge 0,y\ge 0)$ lần lượt là số đơn vị vitamin A và B để một người cần dùng trong một ngày.
Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B nên ta có:
$400\le x+y\le 1000.$
Hàng ngày, tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên ta có: $x\le 600,y\le 500.$
Mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A nên ta có: $0,5x\le y\le 3x.$
Số tiền cần dùng mỗi ngày là: $T\left( x,y \right)=9x+7,5y$
Bài toán trở thành, tìm $x,y$ thỏa mãn hệ $\left( * \right):\left\{ \begin{align} & 0\le x\le 600,0\le y\le 500 \\ & 400\le x+y\le 1000 \\ & 0,5x\le y\le 3x \\ \end{align} \right.$ để $T\left( x,y \right)=9x+7,5y$ đạt giá trị nhỏ nhất.
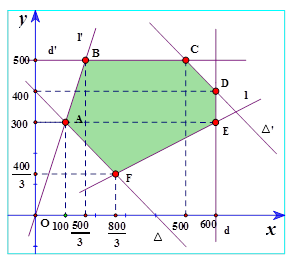
Trong mặt phẳng tọa độ $Oxy,$vẽ các đường thẳng:
$\left( d \right):x-600=0;\left( d’ \right):y-500=0,\left( \Delta \right):x+y-400=0,\left( \Delta ‘ \right):x+y-1000=0,$$\left( l \right):0,5x-y=0,\left( l’ \right):3x-y=0.$
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(lục giác $ABCDEFT\left( x,y \right)=9x+7,5y$đạt tại một trong các điểm:
$A\left( 100;300 \right),B\left( \dfrac{500}{3};500 \right),C\left( 500;500 \right),D\left( 600;400 \right),E\left( 600;300 \right),F\left( \dfrac{800}{3};\dfrac{400}{3} \right)$
Ta có: $T\left( 100;300 \right)=3150,T\left( \dfrac{500}{3};500 \right)=5250,T\left( 500;500 \right)=8250$
$T\left( 600;400 \right)=8400,T\left( 600;300 \right)=7650,T\left( \dfrac{800}{3};\dfrac{400}{3} \right)=3400$
$\Rightarrow$ Giá trị nhỏ nhất của $T\left( x,y \right)=9x+7,5y$ bằng $3150$ khi $x=100,y=300.$
Chọn đáp án D.
Câu 24.
Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.
Cách thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng và 6 hộp Quy sâm.
Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
[A]. Cắt theo cách một $100$ tấm, cắt theo cách hai $300$ tấm.
[B]. Cắt theo cách một $150$ tấm, cắt theo cách hai $100$ tấm.
[C]. Cắt theo cách một $50$ tấm, cắt theo cách hai $300$ tấm.
[D]. Cắt theo cách một $100$ tấm, cắt theo cách hai $200$ tấm.
Gọi x, y lần lượt là số tấm bìa cắt theo cách thứ nhất, thứ hai.
Bài toán đưa đến tìm $x,y\ge 0$ thoả mãn hệ
$\left\{ \begin{align} & 3x\,\,+\,\,2y\,\,\ge \,\,900 \\ & x\,\,+\,\,3y\,\,\ge \,\,1000 \\ & 6x\,\,+\,\,y\,\,=\,\,900 \\ \end{align} \right.$
sao cho $L=x+y$ nhỏ nhất
Trong mặt phẳng tọa độ $Oxy,$
vẽ các đường thẳng:
$\left( d \right):3x+2y-900=0,\left( d’ \right):x+3y-1000=0,\left( \Delta \right):6x+y-900=0.$
Khi đó miền nghiệm của hệ bất phương trình (*) nửa đường thẳng $BC$ nằm trong phần tô màu trên hình vẽ.
$\Rightarrow$ $L=x+y$ nhỏ nhất đạt được tại điểm $B. $
Khi đó, $L\left( x;y \right)=100+300=400.$
Chọn đáp án A.
Câu 25.
Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm $A$ và sản phẩm $B$ trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm $A$ lãi $4$ triệu đồng người ta sử dụng máy $I$ trong $1$ giờ, máy $II$ trong $2$ giờ và máy $III$ trong $3$ giờ. Để sản xuất ra một tấn sản phẩm $B$ lãi được $3$ triệu đồng người ta sử dụng máy $I$ trong $6$ giờ, máy $II$ trong giờ và máy x$III$ trong $2$ giờ. Biết rằng máy $I$ chỉ hoạt động không quá $36$ giờ, máy hai hoạt động không quá $23$ giờ và máy $III$ hoạt động không quá $27$ giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.
[A]. Sản xuất $9$ tấn sản phẩm $A$ và không sản xuất sản phẩm $B. $
[B]. Sản xuất $7$ tấn sản phẩm $A$ và $3$ tấn sản phẩm $B. $
[C]. Sản xuất $\dfrac{10}{3}$ tấn sản phẩm $A$ và $\dfrac{49}{9}$ tấn sản phẩm $B. $
[D]. Sản xuất $6$ tấn sản phẩm $B$ và không sản xuất sản phẩm $A. $
Gọi $x,y$ (tấn) là sản lượng cần sản xuất của sản phẩm $A$ và sản phẩm $B. $ $\left( x,y\ge 0 \right)$
Ta có: $x+6y$ là thời gian hoạt động của máy $I. $
$2x+3y$ là thời gian hoạt động của máy $II. $
$3x+2y$ là thời gian hoạt động của máy $III. $
Số tiền lãi của nhà máy: $T=4x+3y$ (triệu đồng)
Bài toán trở thành: Tìm $x,y$ thỏa mãn hệ $\left\{ \begin{array}{l}
x+6y\le 36 \\
2x+3y\le 23 \\
3x+2y\le 27
\end{array} \right. \,\,\,(*)$ để $T=4x+3y$đạt giá trị lớn nhất.
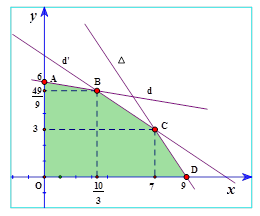
Trong mặt phẳng tọa độ $Oxy,$
vẽ các đường thẳng:
$\left( d \right): x+6y-36=0,\left( d’ \right): 2x+3y-23=0,\left( \Delta
\right): 3x+2y-27=0. $
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(ngũ giác $OABCD$) tô màu trên hình vẽ.
Giá trị lớn nhất của $T=4x+3y$đạt tại một trong các điểm:
$O\left( 0;0 \right),A\left( 0;6 \right),B\left( \dfrac{10}{3};\dfrac{49}{9} \right),C\left( 7;3 \right),D\left( 9;0 \right)$
Khi đó, $T\left( 0;0 \right)=0,T\left( 0;6 \right)=18,T\left( \dfrac{10}{3};\dfrac{49}{9} \right)=\dfrac{89}{3},T\left( 7;3 \right)=37,T\left( 9;0 \right)=36. $
$\Rightarrow $ Giá trị lớn nhất của $T=4x+3y$bằng $37$ khi $x=7,y=3. $
Như vậy, sản xuất $7$ tấn sản phẩm $A$ và $3$ tấn sản phẩm $B. $
Chọn đáp án B.