Dấu của nhị thức bậc nhất, trắc nghiệm toán 10
Câu 1.
Cho \[f(x)=\dfrac{x-1}{2x+5}\]. Khi đó \[f(x)\le 0\]khi
[A]. \[x<\dfrac{-5}{2}. \]
[B]. \[\dfrac{-5}{2}\le x\le 1. \]
[C]. \[\dfrac{-5}{2}<x\le 1. \]
[D]. \[\dfrac{-5}{2}\le x<1. \]

$x-1=0\Leftrightarrow x=1;2x+5=0\Leftrightarrow x=-\dfrac{5}{2}. $
Sử dụng trục số.
Chú ý: $x=-\dfrac{5}{2}$ là giá trị không thỏa mãn.
$f\left( x \right)\le 0\Leftrightarrow -\dfrac{5}{2}<x\le 1. $ Chọn đáp án C.
Câu 2.
Nhị thức nào sau đây nhận giá trị âm với \[x\] nhỏ hơn \[\dfrac{-2}{3}\].
[A]. \[f(x)=-6x-4. \]
[B]. \[f(x)=3x+2. \]
[C]. \[f(x)=-3x-2. \]
[D]. \[f(x)=2x+3. \]
$-6x-4<0\Leftrightarrow x>-\dfrac{2}{3};3x+2<0\Leftrightarrow x<-\dfrac{2}{3}. $
$-3x-2<0\Leftrightarrow x>-\dfrac{2}{3};2x+3<0\Leftrightarrow x<-\dfrac{3}{2}. $ Chọn đáp án B.
Câu 3.
Nghiệm của bất phương trình $\left| x-1 \right|\le 2$ là
[A]. $x<-1\,\,$hoặc $x>3. $
[B]. $-1\le x\le 3. $
[C]. $x\ge 3. $
[D]. $\left[ \begin{array}{l}
x\le 1 \\
x\ge 2
\end{array} \right.. $
$\left| x-1 \right|\le 2\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x-1\ge 0 \\
x-1\le 2
\end{array} \right. \\
\left\{ \begin{array}{l}
x-1<0 \\
-x+1\le 2
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x\ge 1 \\
x\le 3
\end{array} \right. \\
\left[ \begin{array}{l}
x<1 \\
x\ge -1
\end{array} \right.
\end{array} \right. \Leftrightarrow -1\le x\le 3. $ Chọn đáp án B.
Câu 4.
Tập xác định của hàm số \[y=\sqrt{m-2x}-\sqrt{x+1}\] là một đoạn trên trục số khi và chỉ khi
[A]. \[m<-2. \]
[B]. \[m>2. \]
[C]. \[m>\dfrac{-1}{2}. \]
[D]. \[m>-2. \]
Hàm số \[y=\sqrt{m-2x}-\sqrt{x+1}\] xác định\[\Leftrightarrow \left\{ \begin{array}{l}
m-2x\ge 0 \\
x+1\ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x\le \dfrac{m}{2} \\
x\ge -1
\end{array} \right. \].
Tập xác định của hàm số \[y=\sqrt{m-2x}-\sqrt{x+1}\] là một đoạn trên trục số khi \[\dfrac{m}{2}>-1\Leftrightarrow m>-2\].
Chọn đáp án D.
Câu 5.
Tập xác định của hàm số \[y=\sqrt{x-2m}-\sqrt{4-2x}\] là \[\left[ 1;2 \right]\] khi và chỉ khi
[A]. \[m=\dfrac{-1}{2}. \]
[B]. \[m=1. \]
[C]. \[m=\dfrac{1}{2}. \]
[D]. \[m>\dfrac{1}{2}. \]
Hàm số \[y=\sqrt{x-2m}-\sqrt{4-2x}\] xác định \[\Leftrightarrow \left\{ \begin{array}{l}
x-2m\ge 0 \\
4-2x\ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x\ge 2m \\
x\le 2
\end{array} \right. \].
Tập xác định là \[\left[ 1;2 \right]\]khi \[2m=1\Leftrightarrow m=\dfrac{1}{2}\]. Chọn đáp án C.
Câu 6.
Nhị thức nào sau đây nhận giá trị âm với \[x\] nhỏ hơn \[2\]?
[A]. \[f(x)=3x+6. \]
[B]. \[f(x)=6-3x. \]
[C]. \[f(x)=4-2x. \]
[D]. \[f(x)=3x-6. \]
$3x+6<0\Leftrightarrow x<-2;6-3x<0\Leftrightarrow x>2$
$4-2x<0\Leftrightarrow x>2;3x-6<0\Leftrightarrow x<2. $ Chọn đáp án D.
Câu 7.
Với giá trị nào của $m$ thì biểu thức $f(x)=\left( m-2 \right)x+m-5$ là một nhị thức bậc nhất?
[A]. $m>2. $
[B]. $m<2. $
[C]. $m\ne 2\,\,\text{v }\!\!\grave{\mathrm{a}}\!\!\text{ }\,\,\text{m}\ne \text{5}\text{. }$
[D]. $m\ne 2. $
Biểu thức $f\left( x \right)=ax+b$ là một nhị thức bậc nhất khi $a\ne 0$
$\Rightarrow m-2\ne 0\Leftrightarrow m\ne 2. $ Chọn đáp án D.
Câu 8.
Nhị thức \[-5x+1\] nhận giá trị âm khi
[A]. \[x<\dfrac{1}{5}. \]
[B]. \[x<\dfrac{-1}{5}. \]
[C]. \[x>\dfrac{-1}{5}. \]
[D]. \[x>\dfrac{1}{5}. \]
$-5x+1<0\Leftrightarrow x>\dfrac{1}{5}. $ Chọn đáp án D.
Câu 9.
Nhị thức \[2x-4\] nhận giá trị dương khi
[A]. \[x>6. \]
[B]. \[x<6. \]
[C]. \[x>2. \]
[D]. \[x<2. \]
$2x-4>0\Leftrightarrow x>2. $ Chọn đáp án C.
Câu 10.
Nghiệm của bất phương trình \[\left| 2x-3 \right|\le 1\] là
[A]. \[1\le x\le 3. \]
[B]. \[-1\le x\le 1. \]
[C]. \[1\le x\le 2. \]
[D]. \[-1\le x\le 2. \]
TH1: $2x-3\ge 0\Leftrightarrow x\ge \dfrac{3}{2}$ $\Rightarrow $ bpt trở thành: $2x-3\le 1\Leftrightarrow x\le 2. $
Kết hợp điều kiện: $\dfrac{3}{2}\le x\le 2. $
TH2: $2x-3<0\Leftrightarrow x<\dfrac{3}{2}$ $\Rightarrow $ bpt trở thành: $-2x+3\le 1\Leftrightarrow x\ge 1. $
Kết hợp điều kiện: $1\le x<\dfrac{3}{2}. $
Kết hợp $2$ trường hợp ta được: $1\le x\le 2. $ Chọn đáp án C.
Câu 11.
Với giá trị nào của m thì bất phương trình \[mx-{{m}^{2}}>2x-4\] vô nghiệm
[A]. \[m<2. \]
[B]. \[m=2. \]
[C]. \[m>2. \]
[D]. \[m=\pm 2. \]
Ta có : \[mx-{{m}^{2}}>2x-4\Leftrightarrow \left( m-2 \right)x>{{m}^{2}}-4\]
Nếu \[m=2\] khi đó bất phương trình trở thành \[0x>0\] suy ra bất phương trình vô nghiệm.
Chọn đáp án B.
Câu 12.
Cho \[f(x)=\dfrac{2-3x}{5x-1}\] thì $f\left( x \right)>0$ khi
[A]. \[\dfrac{1}{5}<x<\dfrac{2}{3}. \]
[B]. \[\dfrac{1}{5}\le x\le \dfrac{2}{3}. \]
[C]. \[x\le \dfrac{1}{5}\vee x\ge \dfrac{2}{3}. \]
[D]. \[x<\dfrac{1}{5}\vee x>\dfrac{2}{3}. \]
$2-3x=0\Leftrightarrow x=\dfrac{2}{3};5x-1=0\Leftrightarrow x=\dfrac{1}{5}. $
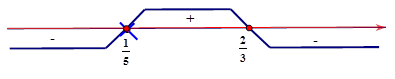
$\Rightarrow f\left( x \right)>0\Leftrightarrow \dfrac{1}{5}<x<\dfrac{2}{3}. $ Chọn đáp án A.
Câu 13.
Biểu thức \[f(x)=\left( -x+3 \right)\left( x+1 \right)\] nhận giá trị dương khi
[A]. \[x>3. \]
[B]. \[-1<x<3. \]
[C]. \[x<-2\vee x>3. \]
[D]. \[x<-1. \]
$-x+3=0\Leftrightarrow x=3;x+1=0\Leftrightarrow x=-1. $
Sử dụng trục xét dấu

$\Rightarrow f\left( x \right)>0\Leftrightarrow -1<x<3. $ Chọn đáp án B.
Câu 14.
Nhị thức \[-3x+2\] nhận giá trị dương khi
[A]. \[x<\dfrac{3}{2}. \]
[B]. \[x<\dfrac{2}{3}. \]
[C]. \[x>\dfrac{-3}{2}. \]
[D]. \[x>\dfrac{2}{3}. \]
$-3x+2>0\Leftrightarrow x<\dfrac{2}{3}. $ Chọn đáp án B.
Câu 15.
Nhị thức \[-2x-3\] nhận giá trị dương khi
[A]. \[x<\dfrac{-3}{2}. \]
[B]. \[x<\dfrac{-2}{3}. \]
[C]. \[x>\dfrac{-3}{2}. \]
[D]. \[x>\dfrac{-2}{3}. \]
$-2x-3>0\Leftrightarrow x<-\dfrac{3}{2}. $ Chọn đáp án A.
Câu 16.
Cho \[a\], \[b\], \[c\], \[d\] là các số thực, trong đó \[a\], \[c\] khác \[0\]. Nghiệm của nhị thức \[ax+b\] nhỏ hơn nghiệm của nhị thức \[cx+d\] khi và chỉ khi
[A]. \[\dfrac{d}{c}<\dfrac{b}{a}. \]
[B]. \[\dfrac{c}{d}<\dfrac{b}{a}. \]
[C]. \[\dfrac{b}{d}>\dfrac{a}{c}. \]
[D]. \[\dfrac{b}{a}<\dfrac{c}{d}. \]
Ta có: \[ax+b=0\Leftrightarrow x=\dfrac{-b}{a}\]; \[cx+d=0\Leftrightarrow x=\dfrac{-d}{c}\].
Theo giả thiết, ta có: \[\dfrac{-b}{a}<\dfrac{-d}{c}\Leftrightarrow \dfrac{b}{a}>\dfrac{d}{c}\]. Chọn đáp án A.
Câu 17.
Tập xác định của hàm số \[y=\sqrt{x-m}-\sqrt{6-2x}\] là một đoạn trên trục số khi và chỉ khi
[A]. \[m=3. \]
[B]. \[m<3. \]
[C]. \[m>3. \]
[D]. \[m<\dfrac{1}{3}. \]
Hàm số \[y=\sqrt{x-m}-\sqrt{6-2x}\] xác định\[\Leftrightarrow \left\{ \begin{array}{l}
x-m\ge 0 \\
6-2x\ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x\ge m \\
x\le 3
\end{array} \right. \].
Tập xác định của hàm số \[y=\sqrt{x-m}-\sqrt{6-2x}\] là một đoạn trên trục số khi\[m<3\]. Chọn đáp án B.
Câu 18.
Trong các biểu thức sau, đâu là một nhị thức bậc nhất?
[A]. $f(x)=2{{x}^{2}}+x+1. $
[B]. $f(x)=2mx+5. $
[C]. $f(x)=2. $
[D]. $f(x)=3x-5. $
Biểu thức $f\left( x \right)=ax+b$ là một nhị thức bậc nhất khi $a\ne 0. $ Chọn đáp án D.
Câu 19.
Nghiệm của bất phương trình $\dfrac{2x+3}{5x-7}>1$ là
[A]. $x<\dfrac{10}{3}. $
[B]. $x>\dfrac{10}{3}. $
[C]. $\dfrac{7}{5}<x<\dfrac{10}{3}. $
[D]. $x<\dfrac{7}{5}. $
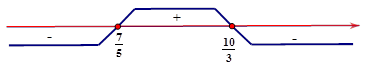
$\dfrac{2x+3}{5x-7}>1\Leftrightarrow \dfrac{2x+3}{5x-7}-1>0\Leftrightarrow \dfrac{-3x+10}{5x-7}>0$
$-3x+10=0\Leftrightarrow x=\dfrac{10}{3};5x-7=0\Leftrightarrow x=\dfrac{7}{5}. $
$\Rightarrow \dfrac{-3x+10}{5x-7}>0\Leftrightarrow \dfrac{7}{5}<x<\dfrac{10}{3}. $ Chọn đáp án C.
Câu 20.
Cho \[f(x)=\dfrac{x-1}{2x+5}\]. Khi đó \[f(x)\le 0\]khi
[A]. \[x<\dfrac{-5}{2}. \]
[B]. \[\dfrac{-5}{2}\le x\le 1. \]
[C]. \[\dfrac{-5}{2}<x\le 1. \]
[D]. \[\dfrac{-5}{2}\le x<1. \]
$x-1=0\Leftrightarrow x=1;2x+5=0\Leftrightarrow x=-\dfrac{5}{2}. $
Sử dụng trục số.

Chú ý: $x=-\dfrac{5}{2}$ là giá trị không thỏa mãn.
$f\left( x \right)\le 0\Leftrightarrow -\dfrac{5}{2}<x\le 1. $ Chọn đáp án C.