Các phép toán trên tập hợp, trắc nghiệm toán lớp 10
Câu 1.
Cho $X=\left\{ 7;2;8;4;9;12 \right\};Y=\left\{ 1;3;7;4 \right\}. $ Tập nào sau đây bằng tập $X\cap Y?$
[A]. $\left\{ 1;2;3;4;8;9;7;12 \right\}. $
[B]. $\left\{ 2;8;9;12 \right\}. $
[C]. $\left\{ 4;7 \right\}. $
[D]. $\left\{ 1;3 \right\}. $
HD: Tập hợp $X\cap Y$ gồm những phần tử vừa thuộc $X$ vừa thuộc $Y$ $\Rightarrow X\cap Y=\left\{ 4;7 \right\}. $ Chọn đáp án C.
Câu 2.
Cho tập hợp $A=\left\{ 2;4;6;9 \right\}$ và $B=\left\{ 1;2;3;4 \right\}. $ Tập hợp $A\backslash B$ bằng tập nào sau đây?
[A]. $\left\{ 1;2;3;5 \right\}. $
[B]. $\left\{ 1;3;6;9 \right\}. $
[C]. $\left\{ 6;9 \right\}. $
[D]. $\varnothing . $
HD: Tập hợp $A\backslash B$ gồm những phần tử thuộc $A$ nhưng không thuộc $B$ $\Rightarrow A\backslash B=\left\{ 6;9 \right\}. $ Chọn đáp án C.
Câu 3.
(NB) Cho $A=\left\{ 0;1;2;3;4 \right\},$ $B=\left\{ 2;3;4;5;6 \right\}. $ Tập hợp $\left( A\backslash B\cap B\backslash A \right)$ bằng
[A]. $\left\{ 0;1;5;6 \right\}. $
[B]. $\left\{ 1;2 \right\}. $
[C]. $\varnothing . $
[D]. $\left\{ 5;6 \right\}. $
HD: Tập hợp $A\backslash B$ gồm những phần tử thuộc $A$ nhưng không thuộc $B$ $\Rightarrow A\backslash B\cap B=\varnothing . $ Chọn đáp án C.
Câu 4.
Cho $A=\left\{ 0;1;2;3;4 \right\},$ $B=\left\{ 2;3;4;5;6 \right\}. $ Tập hợp $A\backslash B$ bằng
[A]. $\left\{ 0 \right\}. $
[B]. $\left\{ 0;1 \right\}. $
[C]. $\left\{ 1;2 \right\}. $
[D]. $\left\{ 1;5 \right\}. $
HD: Tập hợp $A\backslash B$ gồm những phần tử thuộc $A$ nhưng không thuộc $B$ $\Rightarrow A\backslash B=\left\{ 0;1 \right\}. $ Chọn đáp án B.
Câu 5.
Cho $A=\left\{ 0;1;2;3;4 \right\},$ $B=\left\{ 2;3;4;5;6 \right\}. $ Tập hợp $B\backslash A$ bằng
[A]. $\left\{ 5 \right\}. $
[B]. $\left\{ 0;1 \right\}. $
[C]. $\left\{ 2;3;4 \right\}. $
[D]. $\left\{ 5;6 \right\}. $
HD: Tập hợp $B\backslash A$ gồm những phần tử thuộc $B$ nhưng không thuộc $A$ $\Rightarrow B\backslash A=\left\{ 5;6 \right\}. $ Chọn đáp án D.
Câu 6.
Cho $A=\left\{ x\in \mathbb{R}: {{x}^{2}}-7x+6=0 \right\}$ và $B=\left\{ x\in \mathbb{R}: \left| x \right|<4 \right\}. $ Khi đó.
[A]. $A\cup B=A. $
[B]. $A\cap B=A\cup B. $
[C]. $A\backslash B\subset A. $
[D]. $B\backslash A=\varnothing . $
HD: ${{x}^{2}}-7x+6=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=6 \\ \end{align} \right. \Rightarrow A=\left\{ 1;6 \right\}. $ $\left| x \right|<4\Rightarrow -4<x<4\Rightarrow B=\left( -4;4 \right). $ Ta có. $A\backslash B=\left\{ 6 \right\}\subset A. $ Chọn đáp án C.
Câu 7.
Cho $A=\left\{ 1;5 \right\}$ và $B=\left\{ 1;3;5 \right\}. $ Chọn kết quả đúng trong các kết quả sau.
[A]. $A\cap B=\left\{ 1 \right\}. $
[B]. $A\cap B=\left\{ 1;3 \right\}. $
[C]. $A\cap B=\left\{ 1;3;5 \right\}. $
[D]. $A\cap B=\left\{ 1;5 \right\}. $
HD: Tập hợp $A\cap B$ gồm những phần tử vừa thuộc $A$ vừa thuộc $B$ $\Rightarrow A\cap B=\left\{ 1;5 \right\}. $ Chọn đáp án D.
Câu 8.
Lớp $10{{B}_{1}}$ có $7$ học sinh giỏi Toán, $5$ học sinh giỏi Lý, $6$học sinh giỏi Hóa, $3$ học sinh giỏi cả Toán và Lý, $4$ học sinh giỏi cả Toán và Hóa, $2$ học sinh giỏi cả Lý và Hóa, $1$ học sinh giỏi cả $3$ môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp $10{{B}_{1}}$ là.
[A]. $9. $
[B]. $10. $
[C]. $18. $
[D]. $28. $
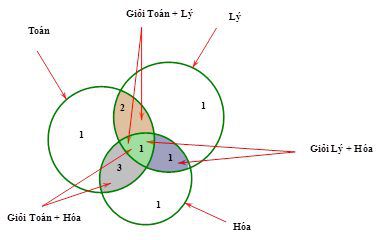
HD: Ta dùng biểu đồ Ven để giải Nhìn vào biểu đồ, số học sinh giỏi ít nhất $1$ trong $3$ môn là. $1+2+1+3+1+1+1=10. $ Chọn đáp án B.
Câu 9.
Cho hai khoảng $A=\left( -\infty ;m \right)$ và \[B=\left( 5;+\infty \right)\]. Khẳng định nào sau đây là đúng?
[A]. $A\cap B=\left( 5;m \right)$ khi $m\,\,\ge 5. $
[B]. $A\cap B=\varnothing $ khi $m\,\,<5. $
[C]. $A\cup B\ne \mathbb{R}$ khi $m\,\,\le \,5. $
[D]. $A\cup B=\mathbb{R}$ khi $m\,\,\ge \,5. $
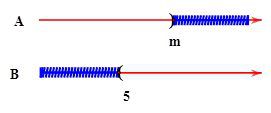
HD:
$A\cap B=\left( 5;m \right)$ khi $m\,\,>5. $,
$A\cap B=\varnothing $ khi $m\,\,\le 5. $ ;
$A\cup B\ne \mathbb{R}$ khi $m\,\,\le \,5. $;
$A\cup B=\mathbb{R}$ khi $m\,\,>\,5. $
Chọn đáp án C.
Câu 10.
Cho $A=\left[ -3;2 \right). $ Tập hợp ${{C}_{\mathbb{R}}}A$ là.
[A]. $\left( -\infty ;-3 \right). $
[B]. $\left( 3;+\infty \right). $
[C]. $\left[ 2;+\infty \right). $
[D]. $\left( -\infty ;-3 \right)\cup \left[ 2;+\infty \right). $
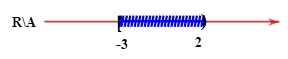
${{C}_{\mathbb{R}}}A=\mathbb{R}\backslash A=\left( -\infty ;-3 \right)\cup \left[ 2;+\infty \right). $ Chọn đáp án D.
Câu 11.
Cho tập hợp ${{C}_{\mathbb{R}}}A=\left[ -3;\sqrt{8} \right)$ và \[{{C}_{\mathbb{R}}}B=\left( -5;2 \right)\cup \left( \sqrt{3};\sqrt{11} \right). \] Tập ${{C}_{\mathbb{R}}}\left( A\cap B \right)$ là.
[A]. $\left( -3;\sqrt{3} \right). $
[B]. $\varnothing . $
[C]. $\left( -5;\sqrt{11} \right). $
[D]. $\left( -3;2 \right)\cup \left( \sqrt{3};\sqrt{8} \right). $
HD: ${{C}_{\mathbb{R}}}A=\mathbb{R}\backslash A=\left[ -3;\sqrt{8} \right)\Rightarrow A=\left( -\infty ;-3 \right)\cup \left[ \sqrt{8};+\infty \right)$ \[{{C}_{\mathbb{R}}}B=\mathbb{R}\backslash B=\left( -5;2 \right)\cup \left( \sqrt{3};\sqrt{11} \right)=\left( -5;\sqrt{11} \right)\Rightarrow B=\left( -\infty ;-5 \right]\cup \left[ \sqrt{11};+\infty \right). \] $\Rightarrow A\cap B=\left( -\infty ;-5 \right]\cup \left[ \sqrt{11};+\infty \right)$ $\Rightarrow {{C}_{\mathbb{R}}}\left( A\cap B \right)=\mathbb{R}\backslash \left( A\cap B \right)=\left( -5;\sqrt{11} \right). $ Chọn đáp án C.
Câu 12.
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp $A=\left[ -4;4 \right]\cup \left[ 7;9 \right]\cup \left[ 1;7 \right). $
[A]. $\left[ -4;9 \right]. $
[B]. $\left( -\infty ;+\infty \right). $
[C]. $\left( 1;8 \right). $
[D]. $\left( -6;2 \right]. $
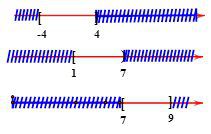
HD: Chọn đáp án A.
Câu 13.
Cho $A=\left[ 1;4 \right],B=\left( 2;6 \right),C=\left( 1;2 \right). $ Tìm $A\cap B\cap C. $
[A]. $\left[ 0;4 \right]. $
[B]. $\left[ 5;+\infty \right). $
[C]. $\left( -\infty ;1 \right). $
[D]. $\varnothing . $
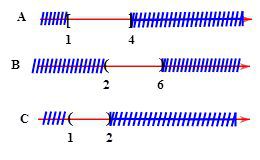
HD: Chọn đáp án D.
Câu 14.
Cho hai tập hợp $A=\left\{ x\in \mathbb{R}: x+3<4+2x \right\}$ và $B=\left\{ x\in \mathbb{R};5x-3<4x-1 \right\}. $ Tìm tất cả các số tự nhiên thuộc cả hai tập $A$ và $B. $
[A]. $0$ và $1. $
[B]. $1. $
[C]. $0. $
[D]. Không có.
HD: $x+3<4+2x\Leftrightarrow x>-1\Rightarrow A=\left( -1;+\infty \right). $ $5x-3<4x-1\Leftrightarrow x<2\Rightarrow B=\left( -\infty ;2 \right). $ $\Rightarrow A\cap B=\left( -1;2 \right)’$ $\Rightarrow $ Có hai số tự nhiên thuộc cả hai tập $A$ và $B$ là $0$ và $1. $ Chọn đáp án A.
Câu 15.
Cho $A=\left[ -4;7 \right]$ và $B=\left( -\infty ;-2 \right)\cup \left( 3;+\infty \right). $ Khi đó, $A\cap B$ là.
[A]. $\left[ -4;-2 \right)\cup \left( 3;7 \right]. $
[B]. $\left[ -4;-2 \right)\cup \left( 3;7 \right). $
[C]. $\left( -\infty ;2 \right]\cup \left( 3;+\infty \right). $
[D]. $\left( -\infty ;-2 \right)\cup \left[ 3;+\infty \right). $
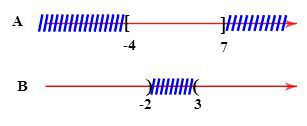
HD: Chọn đáp án A.
Câu 16.
Cho $A=\left( -\infty ;-2 \right]$, $B=\left[ 3;+\infty \right)$và $C=\left( 0;4 \right)$. Khi đó, $\left( A\cup B \right)\cap C$ là.
[A]. $\left[ 3;4 \right]. $
[B]. $\left( -\infty ;-2 \right]\cup \left( 3;+\infty
\right). $
[C]. $\left[ 3;4 \right). $
[D]. $\left( -\infty ;-2 \right)\cup \left[ 3;+\infty
\right). $
HD: $A\cup B=\left( -\infty ;-2 \right]\cup \left[ 3;+\infty \right)$ $\left( A\cup B \right)\cap C=\left[ 3;4 \right). $ Chọn đáp án C.
Câu 17.
Cho $A=\left[ 1;4 \right]$, $B=\left( 2;6 \right),C=\left( 1;2 \right). $ Khi đó, $A\cap B\cap C$ là.
[A]. $\left[ 1;6 \right). $
[B]. $\left( 2;4 \right]. $
[C]. $\left( 1;2 \right]. $
[D]. $\varnothing . $
HD: $A\cap B=\left( 2;4 \right]\Rightarrow A\cap B\cap C=\varnothing . $ Chọn đáp án D.
Câu 18.
Cho $A=\left\{ x|\left( 2x-{{x}^{2}} \right)\left( 2{{x}^{2}}-3x-2 \right)=0 \right\}$ và $B=\left\{ n\in \mathbb{N}*|3<{{n}^{2}}<30 \right\}$. Khi đó, $A\cap B$ bằng.
[A]. $\left\{ 2;4 \right\}. $
[B]. $\left\{ 2 \right\}. $
[C]. $\left\{ 4;5 \right\}. $
[D]. $\left\{ 3 \right\}. $
HD: $\left( {2x – {x^2}} \right)\left( {2{x^2} – 3x – 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} 2x – {x^2} = 0\\ 2{x^2} – 3x – 2 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2\\ x = – \dfrac{1}{2} \end{array} \right.$ $\Rightarrow A=\left\{ -\dfrac{1}{2};0;2 \right\}$ $\left\{ \begin{array}{l} n \in *\\ 3 < {n^2} < 30 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} n \in *\\ \sqrt 3 < n < \sqrt {30} \end{array} \right. \Rightarrow B = \left\{ {2;3;4;5} \right\}$ $\Rightarrow A\cap B=\left\{ 2 \right\}. $ Chọn đáp án B.
Câu 19.
Cho số thực $a<0. $ Điều kiện cần và đủ để $\left( -\infty ;9a \right)\cap \left( \dfrac{4}{a};+\infty \right)\ne \varnothing $ là.
[A]. $-\dfrac{2}{3}<a<0. $
[B]. $-\dfrac{2}{3}\le a<0. $
[C]. $-\dfrac{3}{4}<a<0. $
[D]. $-\dfrac{3}{4}\le a<0. $
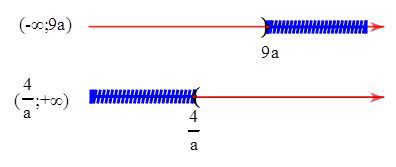
HD: $\left( -\infty ;9a \right)\cap \left( \dfrac{4}{a};+\infty \right)\ne \varnothing $$\Leftrightarrow \dfrac{4}{a}<9a\Leftrightarrow 9{{a}^{2}}<4$ (vì $a<0$ nên khi quy đồng bỏ mẫu dấu bất phương trình bị đổi. ) $\Leftrightarrow {{a}^{2}}<\dfrac{4}{9}\Leftrightarrow -\dfrac{2}{3}<a<\dfrac{2}{3}$ Vì $a<0\Rightarrow -\dfrac{2}{3}<a<0$ Chọn đáp án A.
Câu 20.
Cho số thực $a<0. $ Điều kiện cần và đủ để $\left( -\infty ;a \right)\cup \left[ \dfrac{4}{a};+\infty \right)=\mathbb{R}$ là.
[A]. $a\le -2. $
[B]. $-2\le a\le 2. $
[C]. $-2<a<0. $
[D]. $-2\le a<0. $
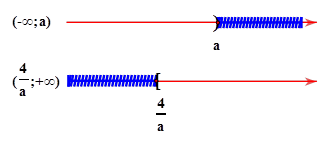
HD: $\left( -\infty ;a \right)\cup \left[ \dfrac{4}{a};+\infty \right)=\mathbb{R}\Leftrightarrow a\ge \dfrac{4}{a}$$\Leftrightarrow {{a}^{2}}\le 4$ (vì $a<0$ nên khi quy đồng bỏ mẫu dấu bất phương trình bị đổi. ) $\Leftrightarrow -2\le a\le 2$ Vì $a<0\Rightarrow -2\le a<0. $ Chọn đáp án D.