Hàm số bậc ba $y=ax^{3}+bx^{2}+cx+d (a \neq 0)$.
Bài toán 1: Cho hàm số $y=ax^{3}+bx^{2}+cx+d$. Khi nào hàm số có hai điểm cực trị.
Phương pháp:
- Đạo hàm hàm bậc ba có dạng $y’=3ax^{2}+2bx+c$
- Để hàm số có cực trị thì phương trình $y’=0$ có hai nghiệm phân biệt $\Leftrightarrow \Delta>0 $ ($\Delta’>0$) hay $b^{2}-3ac>0$
Bài toán 2: Cho hàm số $y=ax^{3}+bx^{2}+cx+d$. Tính khoảng cách giữa hai điểm cực trị.
Phương pháp:
- Bước 1: Tính y’, giải phương trình bằng chức năng EQN và lưu hai nghiệm vào ô nhớ A, B bằng cách nhấn SHIFT RCL.
- Bước 2: Tính giá trị cực trị bằng cách nhập hàm số $ax^{3}+bx^{2}+cx+d$ vào máy và sử dụng phím CALC để lưu vào ô nhớ C và [D].
- Bước 3: Tính $d^{2}=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$ hay $d^{2}=(A-B)^{2}+(C-D)^{2}$.
Ví dụ: Tìm khoảng cách giữa hai điểm cực trị của hàm số $y=x^{3}-4x^{2}+3x-5$

Bài toán 3: Cho hàm số $y=ax^{3}+bx^{2}+cx+d$. Viết phương trình đường thẳng đi qua hai điểm cực trị.
Phương pháp:
Cách 1: Gọi $M(x,y)$ là một điểm cực trị của đồ thị hàm số.
- Ta có $y’=3ax^{2}+2bx+c=0$.
- Hơn nữa, $y=ax^{3}+bx^{2}+cx+d=(\dfrac{1}{3}x+\dfrac{b}{9a})(3ax^{2}+2bx+c)+(\dfrac{2}{3}c-\dfrac{2.b^{2}}{9a})x+d-\dfrac{bc}{9a}$ $=(\dfrac{2}{3}c-\dfrac{2.b^{2}}{9a})x+d-\dfrac{bc}{9a}$.
- Vậy phương trình đường thẳng đi qua hai điểm cực trị là $y=(\dfrac{2}{3}c-\dfrac{2.b^{2}}{9a})x+d-\dfrac{bc}{9a}$
Cách 2: Tìm hai điểm cực trị và viết phương trình đường thẳng đi qua hai điểm cực trị đó.
- Bước 1: Giải phương trình $y’=0$ bằng chức năng EQN và lưu vào ô nhớ A, [B].
- Bước 2: Tính tung độ tương ứng bằng cách nhập hàm và nhấn CAL[C].
- Bước 3: Giải hệ phương trình tìm các hệ số a và b của đường thẳng $ \left \{\begin{matrix} Aa+b=C \\ Ba+b=D \\ \end{matrix} \right.$
Ví dụ: Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số $y=x^{3}-4x^{2}+3x-5$.
Cách 1: Phương trình đường thẳng đi qua hai điểm cực trị là $y=(\dfrac{2}{3}.3-\dfrac{2.(-4)^{2}}{9})x+(-5)-\dfrac{-4.3}{9}=-\dfrac{11}{9}x-\dfrac{11}{3}.$
Cách 2:

Bài toán 4: Bài toán về đồng biến, nghịch biến.
Cách 1: Tính y’
Cách 2: Sử dụng máy tính.
Ví dụ 1: Hàm số $y=\dfrac{x^{2}-2x-5}{x-2}$ đồng biến trên
[A]. $(-\infty,0) \cup (3,+\infty)$.
[B]. $\mathbb{R}$.
[C]. $(0,2) \cup (2,4)$.
[D]. $(-\infty,2) \cup (2,+\infty)$.
Cách 1: $y=\dfrac{x^{2}-2x-5}{x-2}=x-\dfrac{5}{x-2} \Rightarrow y’=1+\dfrac{5}{(x-2)^{2}}>0$ với $\forall x \neq 2$.
Vậy hàm số đã cho đồng biến trên khoảng $ (-\infty,2) \cup (2,+\infty)$. Chọn [D].
Cách 2: Sử dụng trực tiếp Casio để thử đáp án.
- Ta có định lí sau: Giả sử hàm số $f(x)$ có đạo hàm trên khoảng $(a,b)$.
- Nếu $f'(x)>0$ với mọi $x \in (a,b)$ thì hàm số đồng biến trên khoảng $(a,b)$.
- Nếu $f'(x)<0$ với mọi $x \in (a,b)$ thì hàm số nghịch biến trên khoảng $(a,b)$.
$\Rightarrow $ Dùng chức năng tính đạo hàm tại một điểm và gán một giá trị $x_{0}$ nằm trong tập xác định cho trước:
- Nếu kết quả S>0 thì hàm số đã cho đồng biến.
- Nếu kết quả S<0 thì hàm số đã cho nghịch biến.
Cụ thể với bài này: Nhấn tổ hợp SHIFT+ tích phân để tính đạo hàm tại một điểm.
Loại đáp án D vì TXĐ $D=\mathbb{R} \setminus \left\{2 \right\}$.
Nhập

thu được kết quả 6>0 nên loại [A].
Nhập
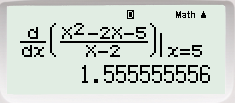
thu được kết quả 1,556>0 nên loại [C].
Ví dụ 2: Để hàm số $y=x^{3}+3mx^{2}-4mx+4$ đồng biến trên $\mathbb{R}$ thì
[A]. $0 \leq m \leq \dfrac{4}{3}$.
[B]. $-\dfrac{4}{3} \leq m \leq 0$.
[C]. $0 \leq m \leq \dfrac{3}{4}$.
[D]. $-\dfrac{3}{4} \leq m \leq 0$.
Bước 1: Nhập dữ liệu với biến x ta gán vào biến X, tham số đi kèm ta gán vào biến Y.
Bước 2: Gán giá trị
Gán giá trị cho biến X: Ta gán một giá trị nào đó trong tập xác định cho trước.
Gán giá trị cho biến Y: Chúng ta quan sát vào các đáp án để gán gia trị cho biến Y.
Cụ thể:
– Nhập dữ liệu


– Gán giá trị (ấn nút CALC)
| Vì tập xác định bằng $\mathbb{R}$ nên gán giá trị X=0. Quan sát đáp án thấy m=0 đáp án nào cũng có nên ta không gán $m=Y=0$. Hai đáp án A và C có chiều như nhau. B và D cũng vậy. |
+ Gán $m=Y=\dfrac{3}{4}$ ta có
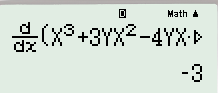
Kết quả <0 nên loại A và [C].
+ Gán $m=Y=-\dfrac{4}{3}$

Kết quả > 0 nên loại [D].
Ví dụ 3: Hàm số $y=\dfrac{m}{3}x^{3}-(m-1)x^{2}+(m-2)x+\dfrac{1}{3}$ đồng biến trên $[2,+\infty)$.
[A]. $m>0.$
[B]. $m \geq 0$.
[C]. $m>8$.
[D]. $m \leq -2$.
Đồng biến trên $[2,+\infty)$ nên gán $X=2$.

Gán $Y=0$, kết quả >0 thì chỉ có B đúng.
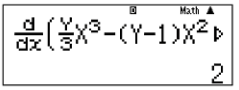
Bài tập áp dụng
Bài 1: Hàm số $y=(m-x)x^{2}-m$ đồng biến trên $(1,2)$ khi
[A]. $a>-3$.
[B]. $a<-3$.
[C]. $a> \dfrac{12}{7}$.
[D]. $a< \dfrac{12}{7}$.
Bài 2: Hàm số $y=x^{3}-3(2m+1)x^{2}+(12m+5)x+2$ đồng biến trên khoảng $(2,+\infty)$ khi
[A]. $-\dfrac{1}{\sqrt{6}} \leq m \leq \dfrac{1}{\sqrt{6}} $.
[B]. $m \leq -\dfrac{1}{\sqrt{6}}$.
[C]. $m \geq \dfrac{5}{12}$.
[D]. $m \leq \dfrac{5}{12}$.
Bài toán 5: Bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất.
Phương pháp:
Nếu hàm số $y=f(x)$ liên tục trên [a,b] và có đạo hàm trong khoảng (a,b) thì luôn có GTLN, GTNN trên đoạn [a,b] và tìm như sau:
- Bước 1: MODE 7
- Bước 2: Nhập hàm $f(x)$ ấn phím = sau đó nhập Start=a, End=b, Step= $\dfrac{b-a}{1}$.
- Bước 3: Dựa vào bảng giá trị, tìm GTLN, GTNN của hàm số.
Ví dụ: Giá trị lớn nhất của hàm số $y=x^{3}-3x^{2}-9x+35$ trên đoạn $[-1,1]$ là
[A]. 40.
[B]. 21.
[C]. 50.
[D]. 35.
- Bước 1: MODE 7
- Bước 2: Nhập $f(X)=X^{3}-3X^{2}-9X+35$ ấn phím = sau đó nhập Start=-1. End=1. Step= 0.2
- Bước 3: Tra bảng nhận được và tìm GTLN
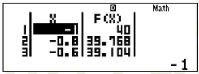
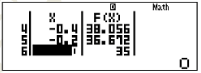
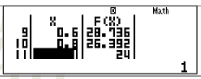
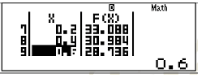
Dựa vào bảng trên, ta thấy GTLN của hàm số là 40.
Chú ý: Cách làm này vẫn đúng khi tìm GTLN và GTNN của một hàm số bất kì trên $[a,b]$.
Tìm GTLN, GTNN của hàm số không cho miền xác định của x.
- Bước 1: Tìm y’
- Bước 2: Tìm nghiệm của phương trình y’=0.
- Bước 3: Tính giá trị của y tại các giá trị của nghiệm trên rồi kết luận.
Bài toán 6: Bài toán tương giao
Phương pháp: Dựa vào đáp án để thử.
Ví dụ: Tìm m để (C): $y=-2x^{3}+6x^{2}+1$ và $d: y=mx+1$ cắt nhau tại 3 điểm phân biệt.
[A]. $m< \dfrac{9}{2}, m\neq 0$.
[B]. $m>\dfrac{9}{2}, m\neq 0$.
[C]. $m<-\dfrac{9}{2}, m \neq 0$.
[D]. $m>-\dfrac{9}{2}, m \neq 0$.
Nhận thấy cả 4 đáp án đều có điều kiện $m \neq 0$ nên ta bỏ qua điều kiện này trong quá trình thử.
– Đầu tiên ta thử với m=5, ta thấy phương trình có 1 nghiệm thực nên loại B, [D].
– Thử tiếp với m=0, ta được phương trình có 3 nghiệm thực nên loại C nhận [A].
- Cách tìm tiệm cận đứng, tiệm cận ngang, khảo sát hàm số
- Các quy tắc tính đạo hàm, toán phổ thông
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số