Dùng đơn điệu hàm số để giải và biện luận phương trình và bất phương trình chứa tham số

Cho hàm số f (x;m) = 0 xác định với mọi x ∈I (*)
- Biến đổi (*) về dạng f (x ) = f (m)
- Xét hàm số y = f (x ) liên tục trên I
- Dùng tính chất đơn điệu của hàm số và kết luận.
Bài tập minh họa
Ví dụ 1: Tìm m để bất phương trình $\sqrt {4x – 2} + 2\sqrt {4 – x} < m$ có nghiệm.
Điều kiện: $\dfrac{1}{2} \le x \le 4$.
Khi đó, bất phương trình $\sqrt {4x – 2} + 2\sqrt {4 – x} < m \Leftrightarrow m > \mathop {\min }\limits_{\left[ {\dfrac{1}{2};4} \right]} \left[ {\sqrt {4x – 2} + 2\sqrt {4 – x} } \right]$
Xét hàm số $f\left( x \right) = \sqrt {4x – 2} + 2\sqrt {4 – x} $ trên $\left[ {\dfrac{1}{2};4} \right]$.
Ta có $f’\left( x \right) = \dfrac{2}{{\sqrt {4x – 2} }} – \dfrac{1}{{\sqrt {4 – x} }} = \dfrac{{2\sqrt {4 – x} – \sqrt {4x – 2} }}{{\sqrt {\left( {4x – 2} \right)\left( {4 – x} \right)} }}$
$f’\left( x \right) = 0 \Leftrightarrow 2\sqrt {4 – x} – \sqrt {4x – 2} \Leftrightarrow x = \dfrac{9}{4};\left( {x \ne \dfrac{1}{2};x \ne 4} \right)$
$f\left( {\dfrac{1}{2}} \right) = \sqrt {14} ;f\left( {\dfrac{9}{4}} \right) = 2\sqrt 7 ;f\left( 4 \right) = \sqrt {14} \Rightarrow \mathop {\min }\limits_{\left[ {\dfrac{1}{2};4} \right]} \left[ {f\left( x \right)} \right] = \sqrt {14} $
Vậy bất phương trình đã cho có nghiệm khi và chỉ khi $m > \sqrt {14} $.
Ví dụ 2: Tìm m để bất phương trình $m\sqrt {2{x^2} + 9} < x + m$ có nghiệm với mọi x.
Ta có $m\sqrt {2{x^2} + 9} < x + m \Leftrightarrow m < \dfrac{x}{{\sqrt {2{x^2} + 9} – 1}}$ , vì $\sqrt {2{x^2} + 9} – 1 > 0,\forall x$
Khi đó, phương trình có nghiệm với mọi x khi và chỉ khi $m < \min \left[ {\dfrac{x}{{\sqrt {2{x^2} + 9} – 1}}} \right]$
Xét hàm số $f\left( x \right) = \dfrac{x}{{\sqrt {2{x^2} + 9} – 1}}$ trên R.
Ta có $f’\left( x \right) = \dfrac{{9 – \sqrt {2{x^2} + 9} }}{{\sqrt {2{x^2} + 9} {{\left( {\sqrt {2{x^2} + 9} – 1} \right)}^2}}} = 0 \Leftrightarrow 9 – \sqrt {2{x^2} + 9} = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 6\\ x = 6 \end{array} \right.$
Bảng biến thiên:
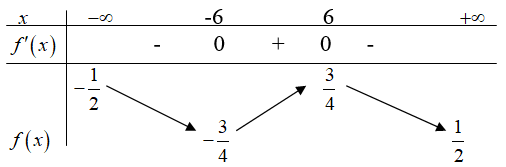
Suy ra $\min \left[ {f\left( x \right)} \right] = – \dfrac{3}{4}$. Do đó bất phương trình nghiệm đúng với mọi x khi $m < – \dfrac{3}{4}$.
Ví dụ 3: Tìm tham số m để bất phương trình sau có nghiệm: $mx – \sqrt {x – 3} \le m + 1$
Điều kiện: $x \ge 3$. Khi đó, $mx – \sqrt {x – 3} \le m + 1 \Leftrightarrow \dfrac{{1 + \sqrt {x – 3} }}{{x – 1}} \ge m$.
Bất phương trình đã cho có nghiệm $x \ge 3$ khi và chỉ khi $m \le \mathop {m{\rm{ax}}}\limits_{\left[ {{\rm{3; + }}\infty } \right)} \left[ {\dfrac{{1 + \sqrt {x – 3} }}{{x – 1}}} \right]$
Xét ham số $f\left( x \right) = \dfrac{{1 + \sqrt {x – 3} }}{{x – 1}}$ trên $\left[ {3; + \infty } \right)$. Ta có $f’\left( x \right) = \dfrac{{5 – x – 2\sqrt {x – 3} }}{{2{{\left( {x – 1} \right)}^2}\sqrt {x – 3} }}$
$f’\left( x \right) = 0 \Rightarrow 5 – x – 2\sqrt {x – 3} = 0 \Leftrightarrow 2\sqrt {x – 3} = 5 – x \Leftrightarrow \left\{ \begin{array}{l} 3 \le x \le 5\\ 4\left( {x – 3} \right) = {\left( {5 – x} \right)^2} \end{array} \right. \Leftrightarrow x = 7 – 2\sqrt 3 $.
Bảng biến thiên
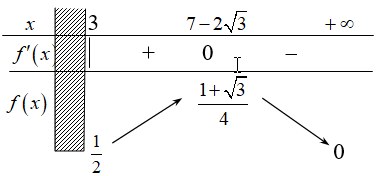
Suy ra $\mathop {m{\rm{ax}}}\limits_{\left[ {{\rm{3; + }}\infty } \right)} \left[ {f\left( x \right)} \right] = \dfrac{{1 + \sqrt 3 }}{4}$ .
Vậy bất phương trình có nghiệm $m \le \dfrac{{\sqrt 3 + 1}}{4}$.
Ví dụ 4: Tìm m để bất phương trình $m{x^2} – 2mx + 3m – 1 \ge 0$ nghiệm đúng với mọi x > 0
Ta biến đổi bất phương trình $m{x^2} – 2mx + 3m – 1 \ge 0 \Leftrightarrow m \ge \dfrac{1}{{{x^2} – 2x + 3}},\forall x > 0 \Leftrightarrow m \ge \mathop {m{\rm{ax}}}\limits_{\left( {0; + \infty } \right)} \left[ {\dfrac{1}{{{x^2} – 2x + 3}}} \right]$
Xét hàm số $f\left( x \right) = \dfrac{1}{{{x^2} – 2x + 3}}$ trên $\left( {0; + \infty } \right)$. Ta có $f’\left( x \right) = \dfrac{{2 – 2x}}{{{{\left( {{x^2} – 2x + 3} \right)}^2}}} = 0 \Leftrightarrow x = 1$
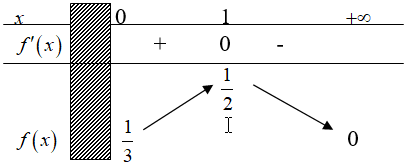
Suy ra $\mathop {m{\rm{ax}}}\limits_{\left( {{\rm{0; + }}\infty } \right)} \left[ {f\left( x \right)} \right] = \dfrac{1}{2}$. Do đó giá trị m cần tìm là $m \ge \dfrac{1}{2}$.
Ví dụ 5: Tìm m để hàm số $y = \dfrac{1}{3}m{x^3} – \left( {m – 1} \right){x^2} + 3\left( {m – 2} \right)x + \dfrac{1}{3}$ đồng biến trên $\left[ {2; + \infty } \right)$.
$y’ = m{x^2} – 2\left( {m – 1} \right)x + 3\left( {m – 2} \right)$.
Hàm số đã cho đồng biến trên $\left[ {2; + \infty } \right)$ khi và chỉ khi
$\begin{array}{l} y’ = m{x^2} – 2\left( {m – 1} \right)x + 3\left( {m – 2} \right) \ge 0,\forall x \in \left[ {2; + \infty } \right)\\ \Leftrightarrow m \ge \dfrac{{6 – 2x}}{{{x^2} – 2x + 3}},\forall x \in \left[ {2; + \infty } \right) \Leftrightarrow m \ge \mathop {m{\rm{ax}}}\limits_{\left[ {2; + \infty } \right)} \left[ {\dfrac{{6 – 2x}}{{{x^2} – 2x + 3}}} \right] \end{array}$
Xét hàm số $g\left( x \right) = \dfrac{{6 – 2x}}{{{x^2} – 2x + 3}}$ trên $\left[ {2; + \infty } \right)$. Ta có $g’\left( x \right) = \dfrac{{2{x^2} – 12x + 6}}{{{{\left( {{x^2} – 2x + 3} \right)}^2}}} = 0 \Leftrightarrow x = 3 \pm \sqrt 6 $
Bảng biến thiên:
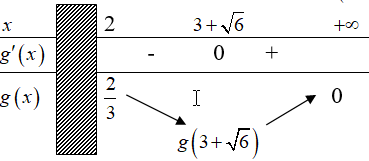
Dựa vào bảng biến thiên suy ra $\mathop {m{\rm{ax}}}\limits_{\left[ {2; + \infty } \right)} \left[ {{\rm{g}}\left( x \right)} \right] = \dfrac{2}{3}$.
Do đó giá trị cần tìm là: $m \ge \dfrac{2}{3}$.
Ví dụ 6: Tìm m để bất phương trình $m{.16^{{\mathop{\rm t}\nolimits} {\rm{anx}}}} – 2m{.4^{{\mathop{\rm t}\nolimits} {\rm{anx}}}} + 2m – 2 \ge 0$ nghiệm đúng với mọi $x \in \left[ {0;\dfrac{\pi }{4}} \right]$.
Đặt $u = {4^{{\mathop{\rm t}\nolimits} {\rm{anx}}}}$. Với $x \in \left[ {0;\dfrac{\pi }{4}} \right] \Rightarrow u \in \left[ {1;4} \right]$. Khi đó bất phương trình đã cho trở thành $m.{u^2} – 2m.u + 2m – 2 \ge 0$. Bất phương trình đã cho nghiệm đúng với mọi $x \in \left[ {0;\dfrac{\pi }{4}} \right]$ khi và chỉ khi $\begin{array}{l} m.{u^2} – 2m.u + 2m – 2 \ge 0,\forall u \in \left[ {1;4} \right]\\ \Leftrightarrow m \ge \dfrac{2}{{{u^2} – 2u + 2}},\forall u \in \left[ {1;4} \right] \Leftrightarrow m \ge \mathop {m{\rm{ax}}}\limits_{\left[ {1;4} \right]} \left[ {\dfrac{2}{{{u^2} – 2u + 2}}} \right] \end{array}$.
Xét hàm số $f\left( u \right) = \dfrac{2}{{{u^2} – 2u + 2}}$ trên [1; 4]. Ta có $f’\left( u \right) = \dfrac{{4\left( {1 – u} \right)}}{{{{\left( {{u^2} – 2u + 2} \right)}^2}}} \le 0,\forall u \in \left[ {1;4} \right]$
Bảng biến thiên
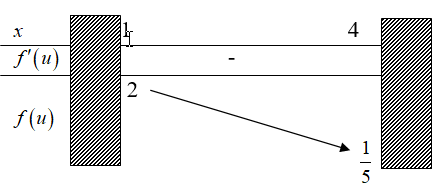
Dựa vào bảng biến thiên suy ra $\mathop {m{\rm{ax}}}\limits_{\left[ {1;4} \right]} \left[ {f\left( u \right)} \right] = 2$. Do đó giá trị cần tìm là: $m \ge 2$.
Ví dụ 7: Tìm m để bất phương trình $1 + {\log _5}\left( {{x^2} + 1} \right) \ge {\log _5}\left( {m{x^2} + 4x + m} \right)$ nghiệm đúng với mọi x .
Ta có $1 + {\log _5}\left( {{x^2} + 1} \right) \ge {\log _5}\left( {m{x^2} + 4x + m} \right) \Leftrightarrow {\log _5}\left[ {5\left( {{x^2} + 1} \right)} \right] \ge {\log _5}\left( {m{x^2} + 4x + m} \right)$
$ \Leftrightarrow \left\{ \begin{array}{l} m{x^2} + 4x + m > 0\\ 5\left( {{x^2} + 1} \right) \ge m{x^2} + 4x + m \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m > \dfrac{{ – 4x}}{{{x^2} + 1}}\\ m \le 5 – \dfrac{{4x}}{{{x^2} + 1}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m > \max \left[ {\dfrac{{ – 4x}}{{{x^2} + 1}}} \right]\\ m \le 5 + \min \left[ {\dfrac{{ – 4x}}{{{x^2} + 1}}} \right] \end{array} \right.$
Xét hàm số $f\left( x \right) = \dfrac{{ – 4x}}{{{x^2} + 1}}$ trên R. Ta có $f’\left( x \right) = \dfrac{{4\left( {{x^2} – 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 1 \end{array} \right.$
Bảng biến thiên
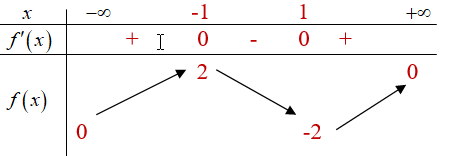
-
Bất phương trình và hệ bất phương trình bậc nhất hai ẩn, trắc nghiệm toán 10