Sử dụng tính đơn điệu của hàm số chứng minh bất đẳng thức
Ta có
- Đưa bất đẳng thức về dạng f (x ) ≥ M,x ∈ (a;b).
- Xét hàm số y = f (x ),x ∈ (a;b).
- Lập bảng biến thiên của hàm số trên khoảng (a;b).
- Dựa vào bảng biến thiên và kết luận.
Lưu ý: Trong một số trường hợp ta phải dung đạo hàm cấp n để xét dấu đạo hàm cấp n-1
Bất đẳng thức một biến
Ví dụ 1: Chứng minh các bất đẳng thức $\,\,{e^x} > 1 + x\,\,\,\,\,khi\,\,x \ne 0$
${e^x} > 1 + x \Leftrightarrow {e^x} – 1 – x > 0$
Đặt :f(x) = ex – 1 – x
D = R
f’(x) = ex – 1
$f'(x) = 0 \Leftrightarrow {e^x} – 1 = 0\,\, \Leftrightarrow x = 0$
Bảng biến thiên:
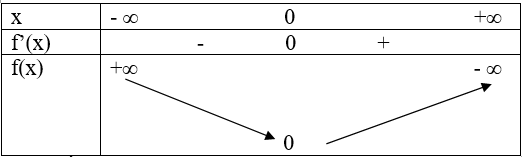
Từ bảng biến thiên suy ra: f(x) ≥ 0 ∀x ( f(x) = 0 tại x = 0) Vậy f(x) > 0 ∀x Hay ex > 1 + x, ∀x ≠ 1
Ví dụ 2: Chứng minh các bất đẳng thức $\sin x < x \Leftrightarrow \sin x – x < 0\,\,khi\,x > 0$
Đặt f(x) = sinx – x
D= R
f’(x) = cosx – 1 => $f'(x) = \cos x – 1 < 0\,\,\forall x \in R$
Bảng biến thiên:
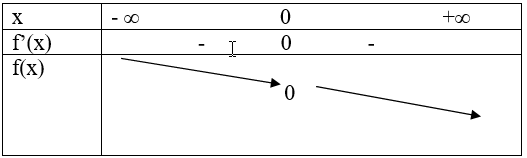
Từ bảng biến thiên suy ra f(x) < 0 khi x > 0 Hay sinx < x khi x > 0
Ví dụ 3: Chứng minh các bất đẳng thức $x – \dfrac{{{x^3}}}{6} < \sin x\,\,\,khi\,\,x > 0$
$x – \dfrac{{{x^3}}}{6} < \sin x\,\, \Leftrightarrow x – \dfrac{{{x^3}}}{6} – \sin x < 0\,\,\,\,\,\,\,khi\,x > 0$
Đặt $f(x) = x – \dfrac{{{x^3}}}{6} – \sin x$
$\begin{array}{l} f'(x) = 1 – \dfrac{{{x^2}}}{2} – \cos x\\ f”(x) = – x + \sin x\, < 0\,\,\,(\sin x < x)\,\,khi\,x > 0 \end{array}$
Bảng biến thiên
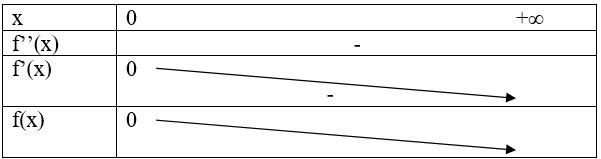
Từ bảng biến thiên suy ra: $f(x) < 0 \Leftrightarrow x – \dfrac{{{x^3}}}{6} < \sin x$
Ví dụ 4: Chứng minh các bất đẳng thức $\dfrac{{2{x^2} + 2x + 3}}{{{x^2} + x + 1}} \le 4\,\,\,\,\,\forall x \in R$
$\begin{array}{l} f(x) = \dfrac{{2{x^2} + 2x + 3}}{{{x^2} + x + 1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D = R\\ f'(x) = – \dfrac{{2x + 1}}{{{{({x^2} + x + 1)}^2}}}\\ f'(x) = 0 \Leftrightarrow x = \dfrac{1}{2} \Leftrightarrow f(\dfrac{1}{2}) = \dfrac{{10}}{3} \end{array}$
Bảng biến thiên
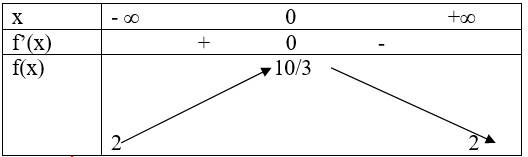
Từ bảng biến thiên suy ra: $f(x) \le \dfrac{{10}}{3} < 4 \Leftrightarrow \dfrac{{2{x^2} + 2x + 3}}{{{x^2} + x + 1}} < 4$
Bất đẳng thức nhiều biến
Lưu ý : Khi chứng minh bất đẳng thức có chứa nhiều biến, ta thường dùng giả thiết, các phép biến đổi đại số, đặt ần phụ hay bất đẳng thức cosi… để đưa về một biến hoặc biến đổi trong bất đẳng thức cần chứng minh xuất hiện các biểu thức đồng dạng.
Ví dụ 5: Chứng minh các bất đẳng thức ${2^{2.\sin x}} + {2^{\tan x}} > {2^{\dfrac{{3x}}{2} + 1}},\,\,\forall x \in (0\,;\dfrac{\pi }{2})$
Nhận xét : Các luỹ thừa trong bất đẳng thức có cùng cơ số, nên chỉ cần so sánh các số mũ, mặt khác vế trái là tổng của các số dương nên ta có thể dùng bđt côsi để làm đơn giản bài toán.
Áp dụng bđt côsi ta có: ${2^{2\sin x}} + {2^{\tan x}} \ge 2\sqrt {{2^{2\sin x}}{{.2}^{\tan x}}} = {2^{\sin x + \dfrac{1}{2}\tan x + 1\,\,\,\,\,\,\,\,\,}}\forall x \in (0;\dfrac{\pi }{2})$
Ta cần chứng minh ${2^{\sin x + \dfrac{1}{2}\tan x + 1}} > {2^{\dfrac{{3x}}{2} + 1}},\,\,\forall x \in (0;\dfrac{\pi }{2})$
Vì a=2>1 nên ta chỉ cần chứng minh: $\sin x + \dfrac{1}{2}\tan x > \dfrac{{3x}}{2}$
Xét hàm số: $f(x) = \sin x + \dfrac{1}{2}\tan x – \dfrac{{3x}}{2}\,,\,\,x \in (0;\dfrac{\pi }{2})$
$\begin{array}{l} f'(x) = \cos x + \dfrac{1}{{2{{\cos }^2}x}} – \dfrac{3}{2} = \dfrac{{(2\cos x + 1){{(1 – \cos x)}^2}}}{{2{{\cos }^2}x}} > 0\,\,\,\,\,\,\forall x \in (0;\dfrac{\pi }{2})\\ f(o) = 0 \end{array}$
Bảng biến thiên
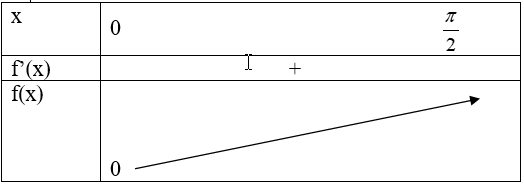
Từ bảng biến thiên suy ra $\sin x + \dfrac{1}{2}\tan x > \dfrac{{3x}}{2}$
Vậy ${2^{2\sin x}} + {2^{\tan x}} > {2^{\dfrac{{3x}}{2} + 1}};\,\,\forall x \in (0;\dfrac{\pi }{2})$
Ví dụ 6: Chứng minh các bất đẳng thức sau: ∀a,b ∈ R: a + b = 2. Hãy chứng minh ${a^4} + {b^4} \ge 2$
Nhận xét: Từ giả thiết ta có Thể tính a theo b hoặc ngược lại, thế vào vế trái ta được hàm số một biến.
Từ giả thiết suy ra: b = a-2. Xét hàm số
$\begin{array}{l} f(a) = {a^4} + {(2 – a)^4};\,a \in ( – \infty : + \infty )\\ f'(a) = 8(a – 1)({a^2} – 2a + 4)\\ Do\,\,\,{a^2} – 2a + 4 > 0\,\forall a\\ f'(a) = 0 \Leftrightarrow a – 1 = 0 \Leftrightarrow a = 1 \Rightarrow f(1) = 2 \end{array}$
Bảng biến thiên
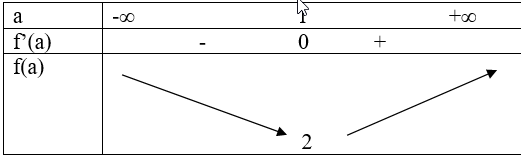
Từ bảng biến thiên suy ra: $f(a) = {a^4} + {(2 – a)^4} \ge 2\forall a\,\,Hay\,\,{a^4} + {b^4} \ge 0\,\forall a,b\,:a + b = 2$
Dấu “=” xảy ra khi a=b=1
Ví dụ 7: Chứng minh các bất đẳng thức $\forall a,b,c > 0:{a^2} + {b^2} + {c^2} = 1$ hãy chứng minh $\,\,\,\,\,\,\,\dfrac{a}{{{b^2} + {c^2}}} + \dfrac{b}{{{c^2} + {a^2}}} + \dfrac{c}{{{a^2} + {b^2}}} \ge \dfrac{{3\sqrt 3 }}{2}$
Nhận xét: Vai trò của a,b,c trong vế trái là như nhau, nên ta có thể biến đổi từng nhóm trong vế trái thành những biểu thức “đồng dạng”
Từ giả thiết suy ra: 0 < a < 1, 0 < b < 1, 0 < c < 1
$\begin{array}{l} \left\{ \begin{array}{l} {b^2} + {c^2} = 1 – {a^2}\\ {c^2} + {a^2} = 1 – {b^2}\\ {a^2} + {b^2} = 1 – {c^2} \end{array} \right.\\ VT = \dfrac{a}{{{b^2} + {c^2}}} + \dfrac{b}{{{c^2} + {a^2}}} + \dfrac{c}{{{a^2} + {b^2}}} = \dfrac{a}{{1 – {a^2}}} + \dfrac{b}{{1 – {b^2}}} + \dfrac{c}{{1 – {c^2}}}\\ \,\,\,\,\,\, = \dfrac{{{a^2}}}{{a(1 – {a^2})}} + \dfrac{{{b^2}}}{{b(1 – {b^2})}} + \dfrac{{{c^2}}}{{c(1 – {c^2})}} \end{array}$
Xét hàm số: f(x) = x(1 – x$^2$) trên đoạn [0 ; 1]
$\begin{array}{l}
f'(x) = 3{x^2} + 1\\
f'(x) = 0 \Leftrightarrow x = \dfrac{1}{{\sqrt 3 }} \Rightarrow f(\dfrac{1}{{\sqrt 3 }}) = \dfrac{2}{{3\sqrt 3 }}
\end{array}$
Bảng biến thiên
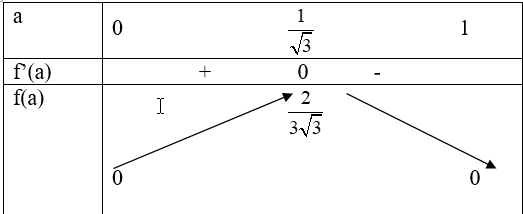
Từ bảng biến thiên suy ra:
$\begin{array}{l} \dfrac{{{a^2}}}{{a(1 – {a^2})}} \ge \dfrac{{3\sqrt 3 {a^2}}}{2}\\ \dfrac{{{b^2}}}{{b(1 – {b^2})}} \ge \dfrac{{3\sqrt 3 {b^2}}}{2}\\ \dfrac{{{c^2}}}{{c(1 – {c^2})}} \ge \dfrac{{3\sqrt 3 {c^2}}}{2}\\ \dfrac{{{a^2}}}{{a(1 – {a^2})}} + \dfrac{{{b^2}}}{{b(1 – {b^2})}} + \dfrac{{{c^2}}}{{c(1 – {c^2})}} \ge \dfrac{{3\sqrt 3 }}{2}({a^2} + {b^2} + {c^2}) = \dfrac{{3\sqrt 3 }}{2}\\ \Leftrightarrow \dfrac{a}{{1 – {a^2}}} + \dfrac{b}{{1 – {b^2}}} + \dfrac{c}{{1 – {c^2}}} \ge \dfrac{{3\sqrt 3 }}{2} \end{array}$
Dấu “=” xảy ra khi $a = b = c = \dfrac{1}{{\sqrt 3 }}$
Nhận xét: Do vai trò của x,y,z bình đẳng nhau nên từ giả thiết suy ra có ít nhất một số không vượt quá 1/3. Mặt khác ta có thể dung bđt Cauchy để sử dụng tính chất bắc cầu và biến đổi về một biến
Giả sử: $0 \le z \le \dfrac{1}{3}$
Ta có:
$\begin{array}{l} xy + yz + zx – 2xyz = xy(1 – 2z) + z(x + y) \ge \dfrac{1}{3}xy + z(x + y) \ge 0\,\,\,\,\,(1)\\ xy + yz + zx – 2xyz = \\ = xy(1 – 2z) + z(x + y) \le {\left( {\dfrac{{x + y}}{2}} \right)^2}(1 – 2z) + z(x + y)\,\,\,\,\,\,\,\,\,\,\,\,(\cos i:x + y \ge 2\sqrt {xy} )\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {\dfrac{{1 – z}}{2}} \right)^2}(1 – 2z) + z(1 – z)\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}( – 2{z^3} + {z^2} + 1) \end{array}$
Xét hàm số:
$\begin{array}{l} f(z) = \dfrac{1}{4}( – 2{z^3} + {z^2} + 1);\,\,\,\,[0;\dfrac{1}{3}]\\ f'(z) = \dfrac{1}{4}( – 6{z^3} + 2z)\\ f'(z) = 0 \Leftrightarrow \left| \begin{array}{l} z = 0 \Rightarrow f(0) = \dfrac{1}{4}\\ z = \dfrac{1}{3} \Rightarrow f(\dfrac{1}{3}) = \dfrac{7}{{27}} \end{array} \right. \end{array}$
Bảng biến thiên
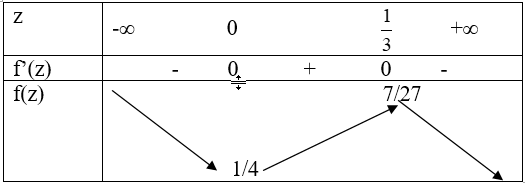
Từ bảng biến thiên suy ra: $f(z) \le \dfrac{7}{{27}}\,\,\,\,\,khi\,z \in [0;\dfrac{1}{3}]$
Hay xy + yz + zx – 2xyz ≤ 7/27 (2)
Từ (1),(2) suy ra: $0 \le xy + yz + zx – 2xyz \le \dfrac{7}{{27}}\,\,\,\,\forall x,y,z \ge 0\,,\,x + y + z = 1$
Ví dụ 8: Chứng minh rằng: $x – \dfrac{{{x^3}}}{{3!}} < \sin x < x – \dfrac{{{x^3}}}{{3!}} + \dfrac{{{x^5}}}{{5!}}$ ∀x > 0
$x – \dfrac{{{x^3}}}{{3!}} < \sin x$ ∀x > 0 <=> $f\left( x \right) = \dfrac{{{x^3}}}{{3!}} – x + \sin x > 0$ ∀x > 0
Ta có $f’\left( x \right) = \dfrac{{{x^2}}}{{2!}} – 1 + \cos x$ => $f”\left( x \right) = x – \sin x$ => $f”’\left( x \right) = 1 – \cos x \ge 0$ ∀x > 0
=> f”(x) đồng biến [0, +∞) => $f”\left( x \right) > \,f”\left( 0 \right) = 0$ ∀x > 0
=> f’(x) đồng biến [0, +∞) => $f’\left( x \right) > f’\left( 0 \right)$ = 0 ∀x > 0
=> f(x) đồng biến [0, +∞) => f(x) > f(0) = 0 ∀x > 0 => (đpcm)
$\sin x < x – \dfrac{{{x^3}}}{{3!}} + \dfrac{{{x^5}}}{{5!}}$ ∀x > 0 <=> g(x) = $\dfrac{{{x^5}}}{{5!}} – \dfrac{{{x^3}}}{{3!}} + x – \sin x > 0$ ∀x > 0
Ta có g'(x) = $\dfrac{{{x^4}}}{{4!}} – \dfrac{{{x^2}}}{{2!}} + 1 – \cos x$=> g”(x) = $\dfrac{{{x^3}}}{{3!}} – x + \sin x$ = f(x) > 0 ∀x > 0
=> g'(x) đồng biến [0, +∞) => g'(x) > g'(0) = 0 ∀x > 0
=> g(x) đồng biến [0, +∞) => g(x) > g (0) = 0 ∀x > 0 => (đpcm)
Ví dụ 9: Chứng minh các bất đẳng thức $\sin x > \dfrac{{2x}}{\pi }\quad \forall x \in \left( {0,\dfrac{\pi }{2}} \right)$
$\sin x > \dfrac{{2x}}{\pi } \Leftrightarrow f(x) = \dfrac{{\sin x}}{x} > \dfrac{2}{\pi }$ ∀x∈ (0; π/2). Xét biểu thức đạo hàm $f'(x) = \dfrac{{x\cos x – \sin x}}{{{x^2}}} = \dfrac{{g(x)}}{{{x^2}}}$, ở đây kí hiệu g(x) = x cosx – sinx
Ta có g’(x) = cosx – xsinx – cosx = – xsinx < 0 ∀x∈(0; π/2)
=> g(x) giảm trên (0; π/2) => g(x) < g(0) = 0
=> $f’\left( x \right) = \dfrac{{g(x)}}{{{x^2}}} < 0$ ∀x∈(0; π/2)=> f (x) giảm trên (0; π/2)
=> $f\left( x \right) > f\left( {{\textstyle{\pi \over 2}}} \right) = \dfrac{2}{\pi }$ <=> $\sin x > \dfrac{{2x}}{\pi },\quad \forall x \in \left( {0,\dfrac{\pi }{2}} \right)$
Ví dụ 10: Chứng minh các bất đẳng thức $\dfrac{1}{{y – x}}\left( {\ln \dfrac{y}{{1 – y}} – \ln \dfrac{x}{{1 – x}}} \right) > 4;\,\left\{ \begin{array}{l} \forall x,y \in \left( {0,1} \right)\\ x \ne y \end{array} \right.$ (1)
Xét hai khả năng sau đây:
+ Nếu y > x thì (1) <=> $\ln \dfrac{y}{{1 – y}} – \ln \dfrac{x}{{1 – x}} > 4\left( {y – x} \right) \Leftrightarrow \ln \dfrac{y}{{1 – y}} – 4y > \ln \dfrac{x}{{1 – x}} – 4x$
+ Nếu y < x thì (1) <=> $\ln \dfrac{y}{{1 – y}} – \ln \dfrac{x}{{1 – x}} < 4\left( {y – x} \right) \Leftrightarrow \ln \dfrac{y}{{1 – y}} – 4y < \ln \dfrac{x}{{1 – x}} – 4x$
Xét hàm đặc trưng f(t) = $\ln \dfrac{t}{{1 – t}} – 4t$ với t∈(0, 1).
Ta có $f’\left( t \right) = \dfrac{1}{{t(1 – t)}} – 4 = \dfrac{{{{\left( {2t – 1} \right)}^2}}}{{t(1 – t)}} > 0$ ∀t∈(0,1) => f(t) đồng biến (0, 1)
=> f( y ) > f( x ) nếu y > x và f( y ) < f( x ) nếu y < x => (đpcm)
Ví dụ 11: Chứng minh các bất đẳng thức ${a^b} < {b^a}{^{^{^{}}}_{}}$ ∀a > b ≥ e
${a^b} < {b^a} \Leftrightarrow \ln \left( {{a^b}} \right) < \ln \left( {{b^a}} \right) \Leftrightarrow b\ln \left( a \right) < a\ln \left( b \right) \Leftrightarrow \dfrac{{\ln a}}{a} < \dfrac{{\ln b}}{b}$
Xét hàm đặc trưng f(x) = $\dfrac{{\ln x}}{x}$ ∀x ≥ e.
Ta có $f'(x) = \dfrac{{1 – \ln x}}{{{x^2}}} \le \dfrac{{1 – \ln e}}{{{x^2}}} = 0$ => f(x) nghịch biến [e, +∞)
=> f(a) < f(b) <=> $\dfrac{{\ln a}}{a} < \dfrac{{\ln b}}{b} \Leftrightarrow {a^b} < {b^a}$
Ví dụ 12: Chứng minh các bất đẳng thức ${\left( {{2^a} + {\textstyle{1 \over {{2^a}}}}} \right)^b} \le {\left( {{2^b} + {\textstyle{1 \over {{2^b}}}}} \right)^a},\forall a \ge b > 0$
Biến đổi bất đẳng thức ${\left( {{2^a} + {\textstyle{1 \over {{2^a}}}}} \right)^b} \le {\left( {{2^b} + {\textstyle{1 \over {{2^b}}}}} \right)^a} \Leftrightarrow {\left( {{\textstyle{{1 + {4^a}} \over {{2^a}}}}} \right)^b} \le {\left( {{\textstyle{{1 + {4^b}} \over {{2^b}}}}} \right)^a}$
$ \Leftrightarrow {\left( {1 + {4^a}} \right)^b} \le {\left( {1 + {4^b}} \right)^a} \Leftrightarrow \ln {\left( {1 + {4^a}} \right)^b} \le \ln {\left( {1 + {4^b}} \right)^a} \Leftrightarrow {\textstyle{{\ln \left( {1 + {4^a}} \right)} \over a}} \le {\textstyle{{\ln \left( {1 + {4^b}} \right)} \over b}}$.
Xét hàm số đặc trưng cho hai vế $f\left( x \right) = {\textstyle{{\ln \left( {1 + {4^x}} \right)} \over x}}$với x > 0. Ta có $f’\left( x \right) = {\textstyle{{{4^x}\ln {4^x} – \left( {1 + {4^x}} \right)\ln \left( {1 + {4^x}} \right)} \over {{x^2}\left( {1 + {4^x}} \right)}}} < 0 \Rightarrow f\left( x \right)$giảm trên$\left( {0, + \infty } \right) \Rightarrow f\left( a \right) \le f\left( b \right)$
Ví dụ 13: Chứng minh các bất đẳng thức $\dfrac{a}{{b + c}} + \dfrac{b}{{c + a}} + \dfrac{c}{{a + b}} \ge \dfrac{3}{2}$ ∀a, b, c > 0 (1)
Không mất tính tổng quát, giả sử a ≥ b ≥ c. Đặt x = a => x ≥ b ≥ c > 0.
Ta có (1) <=> f (x) = $\dfrac{x}{{b + c}} + \dfrac{b}{{c + x}} + \dfrac{c}{{x + b}}$ với x ≥ b ≥ c > 0
=> $f'(x) = \dfrac{1}{{b + c}} – \dfrac{b}{{{{\left( {x + c} \right)}^2}}} – \dfrac{c}{{{{\left( {x + b} \right)}^2}}} > \dfrac{1}{{b + c}} – \dfrac{b}{{{{\left( {b + c} \right)}^2}}} – \dfrac{c}{{{{\left( {b + c} \right)}^2}}} = 0$
=> f(x) đồng biến [b, +∞) => $f(x) \ge f(b) = \dfrac{{2b + c}}{{b + c}}$ (2)
Đặt x = b => x ≥ c > 0, xét hàm số g(x) = $\dfrac{{2x + c}}{{x + c}}$ với x ≥ c > 0
=> $g'(x) = \dfrac{c}{{{{\left( {x + c} \right)}^2}}} > 0$ ∀c > 0 => g(x) đồng biến [c, +∞) => $g(x) \ge g(c) = \dfrac{3}{2}$ (3)
Từ (2), (3) suy ra $\dfrac{a}{{b + c}} + \dfrac{b}{{c + a}} + \dfrac{c}{{a + b}} \ge \dfrac{3}{2}$ ∀a, b, c > 0