Xét chiều biến thiên của hàm số

Xét chiều biến thiên của hàm số y = f (x) ta thực hiện các bước sau:
- Tìm tập xác định D của hàm số .
- Tính đạo hàm y’ = f'(x ) .
- Tìm các giá trị của x thuộc D để f'(x ) = 0 hoặc f'(x ) không xác định( ta gọi đó là điểm tới hạn hàm số ).
- Xét dấu y ‘ = f'(x ) trên từng khoảng x thuộc D.
- Dựa vào bảng xét dấu và điều kiện đủ suy ra khoảng đơn điệu của hàm số.
Ví dụ 1: Xét chiều biến thiên của các hàm số sau: \( y = {{x + 2} \over {x – 1}} \)
Hàm số đã cho xác định trên khoảng ( – ∞;1)∪ (1;+∞) Vậy hàm số đồng biến trên mỗi khoảng ( – ∞;1)∪ (1;+∞) Ví dụ 2: Xét chiều biến thiên của các hàm số sau: \( y = {{ – {x^2} + 2x – 1} \over {x + 2}} \)
Hàm số đã cho xác định trên khoảng ( – ∞;- 2)∪ (- 2;+∞) Vậy, hàm số đồng biến trên các khoảng (−5;−2) và (−2;1), nghịch biến trên các khoảng (−∞;−5) và (1;+∞). Đối với hàm \(y=\dfrac{ax+b}{cx+d},\,\left( ac\ne 0 \right)\) luôn đồng biến hoặc luôn nghịch biến trên từng khoảng xác định của nó. Ví dụ 3: Xét chiều biến thiên của hàm số sau: \(y=-{{x}^{3}}-3{{x}^{2}}+24x+26\)
Hàm số đã cho xác định trên ℝ . + Trên khoảng(−4;2): y ‘ > 0 ⇒ y đồng biến trên khoảng (−4;2), Ví dụ 4: Xét chiều biến thiên của hàm số sau: \(y={{x}^{4}}-6{{x}^{2}}+8x+1\)
Giải Vậy,hàm số đồng biến trên khoảng (−2;+∞) và nghịch biến trên khoảng (−∞;−2). Ví dụ 5: Xét chiều biến thiên của các hàm số sau: \(y=\sqrt{{{x}^{2}}-2x}\) Giải Hàm số không có đạo hàm tại các điểm x = 0,x = 2. Vậy , hàm số nghịch biến trên khoảng (−∞;0)và đồng biến trên khoảng (2;+∞) Ví dụ 6: Xét chiều biến thiên của các hàm số sau: \(y=\sqrt{3{{x}^{2}}-{{x}^{3}}}\) Giải Hàm số đồng biến trên khoảng (0;2) , nghịch biến trên các khoảng (−∞;0) và (2;3). Ví dụ 7: Xét chiều biến thiên của các hàm số sau: \(y=x\sqrt{1-{{x}^{2}}}\) Giải Trên khoảng (- 1; 1): y’ = 0 \(\Leftrightarrow x=\pm \dfrac{\sqrt{2}}{2}\) Hàm số đồng biến trên khoảng \(\left( \dfrac{-\sqrt{2}}{2};\dfrac{\sqrt{2}}{2} \right)\) nghịch biến trên mỗi khoảng \(\left( -1;-\dfrac{\sqrt{2}}{2} \right)\) và \(\left( \dfrac{\sqrt{2}}{2};1 \right)\) Ví dụ 8: Xét chiều biến thiên của các hàm số sau: \(y=x+1-2\sqrt{{{x}^{2}}+3x+3}\) Giải Ví dụ 9: Xét chiều biến thiên của các hàm số sau: \(y=\left| {{x}^{2}}-2x-3 \right|\) Giải Hàm số đồng biến trên mỗi khoảng(-1;1) và (3; +X) , nghịch biến trên mỗi khoảng (-X; -1) và (1; 3) Ví dụ 10: Xét chiều biến thiên của các hàm số sauy = 2sin(x) + cos(2x) trên đoạn [0; π] Giải Trên đoạn [0; π]: $y’ = 0 \Leftrightarrow \left\{ \begin{gathered} x \in \left[ {0;\pi } \right] \hfill \\ \left[ \begin{gathered} \cos \left( x \right) = 0 \hfill \\ \sin \left( x \right) = \dfrac{1}{2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow x = \dfrac{\pi }{2} \vee x = \dfrac{\pi }{6} \vee x = \dfrac{{5\pi }}{6}$ Dựa vào bảng biến thiên suy ra: hàm số đồng biến trên các khoảng (0; π/6) và (π/2; 5π/6), nghịch biến trên các khoảng (π/6; π/2) và (5π/6; π) Ví dụ 11: Chứng minh rằng hàm số y = 2sin(x) + cos(x) đồng biến trên đoạn [0; π/3] và nghịch biến trên đoạn [π/3; π] Hàm số đã cho xác định trên đoạn [0; π] Ví dụ 12. Chứng minh rằng: f(x) = cos(2x) – 2x + 3 nghịch biến trên R. Ta có: $f'(x) = – 2(\sin 2x + 1) \le 0,\,\,\forall x \in R$ và $f'(x) = 0 \Leftrightarrow \sin 2x = – 1 \Leftrightarrow x = – \dfrac{\pi }{4} + k\pi ,\,\,k \in Z$ Ví dụ 13. Chứng minh rằng: $f\left( x \right) = x + {\cos ^2}x$ đồng biến trên R. Ta có: f’(x) = 1 – sin2x; $f'(x) = 0 \Leftrightarrow \sin 2x = 1 \Leftrightarrow x = \dfrac{\pi }{4} + k\pi ,\,\,k \in Z$
Ta có \(\ y’ = – \dfrac{3}{{{{\left( {x – 1} \right)}^2}}} < 0,\forall x \ne 1\)
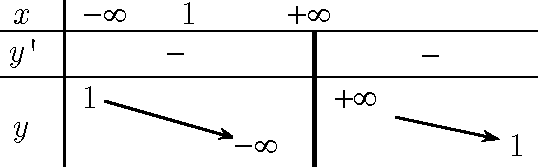
Ta có: \(y’=\dfrac{-{{x}^{2}}-4x+5}{{{\left( x+2 \right)}^{2}}},\forall \ne -2\Rightarrow y’=0\Leftrightarrow \left[ \begin{align} & x=-5 \\ & x=1 \\ \end{align} \right.\)
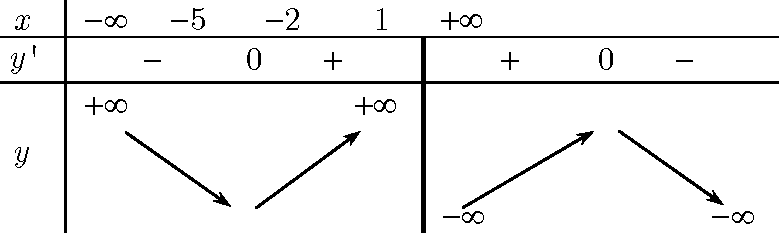
* Ta có: \(y’=-3{{x}^{2}}-6x+24\Rightarrow y’=0\Leftrightarrow -3{{x}^{2}}-6x+24=0\Leftrightarrow \left[ \begin{align} & x=-4 \\ & x=2 \\ \end{align} \right.\)
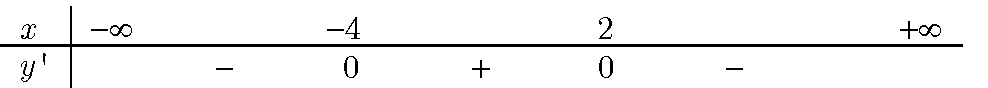
+ Trên mỗi khoảng (−∞;−4), (2;+∞) :y ‘ < 0 ⇒ y nghịch biến trên các khoảng(−∞;−4), (2;+∞) .
Hàm số đã cho xác định trên ℝ .
Ta có: \(y’=4{{x}^{3}}-12x+8=4{{\left( x-1 \right)}^{2}}\left( x+2 \right)\Rightarrow y’=0\Leftrightarrow 4{{\left( x-1 \right)}^{2}}\left( x+2 \right)=0\Leftrightarrow \left[ \begin{align} & x=-2 \\ & x=1 \\ \end{align} \right.\)
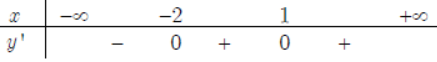
Nhận xét:
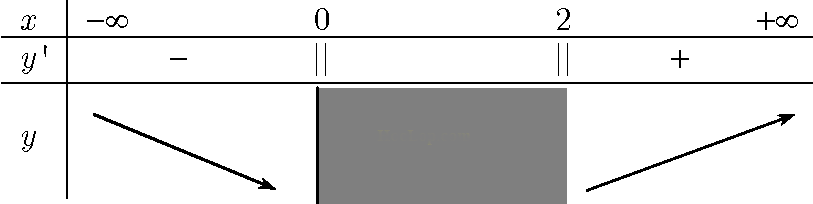
* Hàm số đã cho xác định trên nửa khoảng (−∞;3].
* Ta có: \(y’=\dfrac{3\left( 2x-{{x}^{2}} \right)}{2\sqrt{3{{x}^{2}}-{{x}^{3}}}},\forall x\in \left( -\infty ;0 \right)\cup \left( 0;3 \right)\)
Hàm số không có đạo hàm tại các điểmx = 0, x = 3 .
Suy ra, trên mỗi khoảng (−∞;0) và (0;3): y ‘ = 0 ⇔ x = 2
Bảng biến thiên: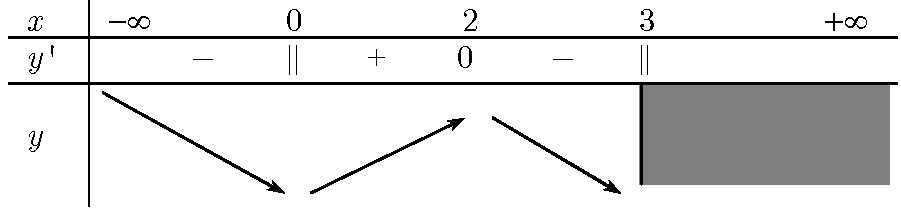
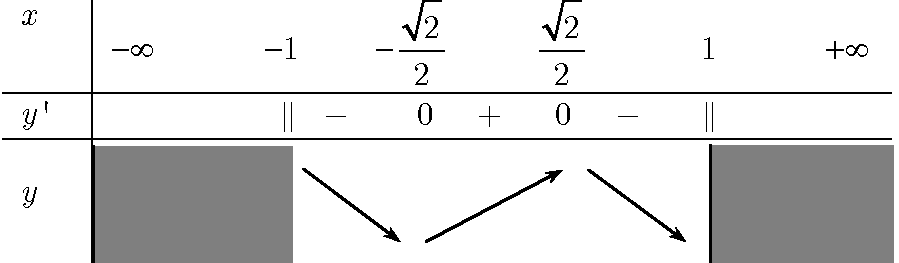
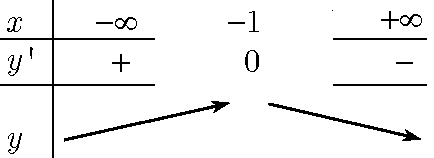
* Hàm số đã cho xác định trên R
* Ta có \(y’=\left\{ \begin{align} & 2x-2\,\,khix\le -1\vee x\ge 3 \\ & –2x+2\,\,khi-1<x<3 \\ \end{align} \right.\)
Hàm số không có đạo hàm tại x = -1 và x = 3.
+ Trên khoảng (—1; 3) : y’ = 0 x = 1;
+ Trên khoảng (—X;—1): y ‘ < 0;
+ Trên khoảng (3; +X): y ‘ > 0.
Bảng biến thiên:

Bảng biến thiên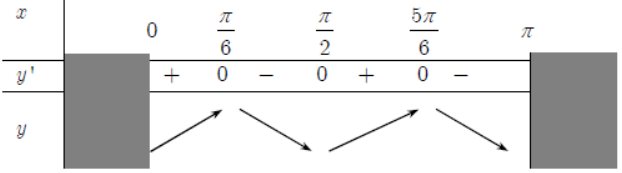
Ta có: y’ = sinx(2cosx – 1); x ∈ [0; π]
Vì x ∈ [0; π] => sinx > 0 nên đoạn (0; π): y’ = 0 <=>cosx = 0,5 <=>x = π/3
Trên khoảng (0; π/3): y’ > 0 nên hàm số đồng biến trên đoạn [0; π/3]
Trên khoảng (π/3; π): y’ < 0 nên hàm số đồng biến trên đoạn [π/3; π]
Hàm số f liên tục trên mỗi đoạn $\left[ { – \dfrac{\pi }{4} + k\pi ; – \dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right]$ và có đạo hàm f’(x) < 0 với mọi $x \in \left( { – \dfrac{\pi }{4} + k\pi ; – \dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right),\,\,k \in Z$.
Do đó, hàm số nghịch biến trên mỗi đoạn $\left[ { – \dfrac{\pi }{4} + k\pi ; – \dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right],\,\,k \in Z$.
Vậy hàm nghịch biến trên R.
NX: Hàm số f liên tục trên mỗi đoạn $\left[ {\dfrac{\pi }{4} + k\pi ;\dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right]$ và có đạo hàm f’(x) > 0 với mọi $x \in \left( {\dfrac{\pi }{4} + k\pi ;\dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right),\,\,k \in Z$.
Do đó hàm số đồng biến trên mỗi đoạn $\left[ {\dfrac{\pi }{4} + k\pi ;\dfrac{\pi }{4} + \left( {k + 1} \right)\pi } \right],\,\,k \in Z$.
Vậy hàm đồng biến trên R.