Đại cương về đường thẳng và mặt phẳng

1. Điểm, đường thẳng, mặt phẳng
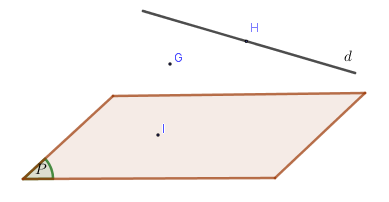
Quan sát hình vẽ trên ta có:
– Điểm \(H\) thuộc đường thẳng \(d\), kí hiệu \(H \in d\).
– Điểm \(I\) thuộc mặt phẳng \(\left( P \right)\), kí hiệu \(I \in \left( P \right)\).
– Điểm \(G\) không thuộc đường thẳng \(d\) và không thuộc mặt phẳng \(\left( P \right)\), kí hiệu \(G \notin d,G \notin \left( P \right)\).
2. Các tính chất
– Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
– Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
– Nếu một đường thẳng có hai điểm phân biệt cùng thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
– Có bốn điểm không cùng thuộc một mặt phẳng.
– Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
Do đó: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua điểm chung ấy. Đường thẳng đó được gọi là giao tuyến của hai mặt phẳng .
– Trên mỗi mặt phẳng các, kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định một mặt phẳng
Một mặt phẳng được xác định nếu ta biết nó đi qua:
– Ba điểm không thẳng hàng. (chẳng hạn $mp\left( {ABC} \right),\left( {ABC} \right)$)
– Một điểm và một đường thẳng không đi qua điểm đó. (ví dụ $mp\left( {A,d} \right)$)
– Hai đường thẳng cắt nhau. (ví dụ $mp\left( {a,b} \right)$)
4. Giao tuyến của hai mặt phẳng
Giả sử \(\left( P \right),\left( Q \right)\) là hai mặt phẳng phân biệt có điểm chung \(A\). Khi đó, \(\left( P \right),\left( Q \right)\) có đường thẳng chung duy nhất \(a\) đi qua \(A\). Đường thẳng \(a\) được gọi là giao tuyến của hai mặt phẳng.
Đường thẳng \(a\) được gọi là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\), kí hiệu \(a = \left( P \right) \cap \left( Q \right)\).
5. Các quy tắc vẽ hình, biểu diễn của hình không gian
– Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
– Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
– Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
– Đường nhìn thấy vẽ nét liền, đường bị che khuất vẽ nét đứt.
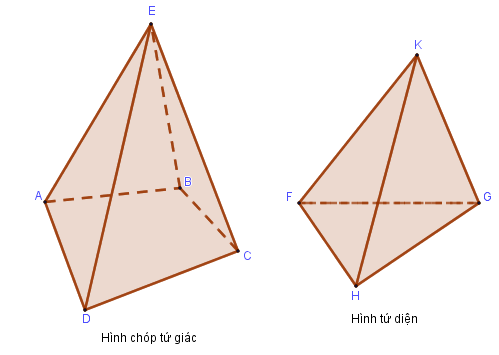
6. Hình chóp và hình tứ diện